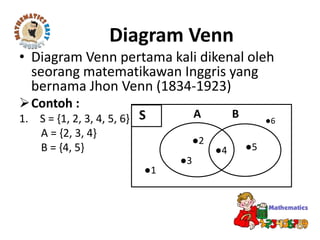
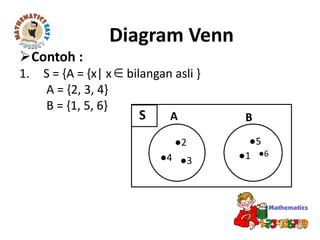
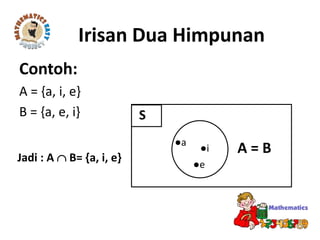
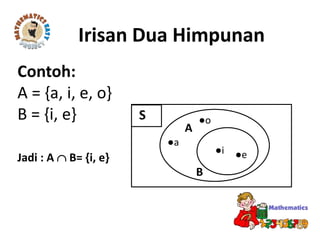
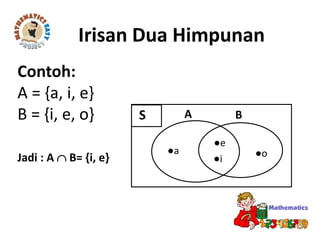
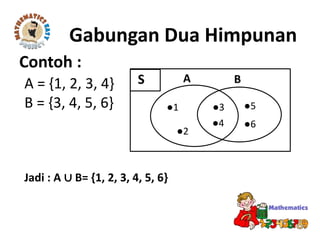
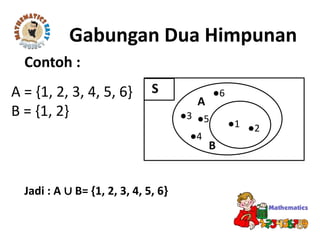
Dokumen tersebut membahas tentang standar kompetensi dan kompetensi dasar mengenai konsep himpunan dan diagram Venn dalam pemecahan masalah. Terdapat penjelasan mengenai pengertian himpunan, anggota himpunan, himpunan bagian, operasi himpunan seperti irisan, gabungan, dan komplemen, serta penyajian himpunan dengan diagram Venn.

2. DoliSyahputra, ST

3. HIMPUNAN

4. SK & KD
Standar Kompetensi
Menggunakan konsep himpunan dan diagram Venn dalam pemecahan masalah.
Kompetensi Dasar
4.1 Memahami pengertian dan notasi himpunan, serta penyajiannya.
4.2 Memahami konsep himpunan bagian.
4.3 Melakukan operasi irisan, gabungan, kurang (difference), dan komplemen pada
himpunan.
4.4 Menyajikan himpunan dengan diagram Venn.
4.5 Mengggunakan konsep himpunan dalam pemecahan masalah.
Indikator
4.4.1 Menyajikan irisan dan gabungan dengan diagram Venn.
Tujuan Pembelajaran
Peserta didik dapat menyajikan irisan dan gabungan suau himpunan dengan diagram venn.
LATIHAN SOALMATERI PENYUSUNSK & KD

6. Apa itu
Himpunan …. ???

7. Himpunan hewan berkaki empat

8. Himpunan hewan yang berkembang biak
dengan cara bertelur

9. Himpunan hewan berkaki dua

10. Himpunan alat elektronik

11. Himpunan alat musik tradisional

12. Himpunan huruf dalam abjad

13. Himpunan huruf vokal dalam abjad

14. Himpunan adalah
kumpulan dari benda atau
objek yang terdefinisi
dengan jelas

15. bagaimana
dengan ini ….
???

16. bukan himpunan, karena sebuah bunga bisa dikatakan
indah oleh kita, tetapi orang lain belum tentu.

17. bukan himpunan, karena sebuah lukisan bisa dikatakan
indah oleh kita tetapi orang lain belum tentu.

18. bukan himpunan, karena seorang cowok bisa dikatakan
ganteng oleh kita, tetapi orang lain belum tentu.

19. bukan himpunan, karena seorang cewek bisa dikatakan
cantik oleh kita, tetapi orang lain belum tentu.

20. Anggota dan Bukan Anggota Himpunan
Setelah mengetahui bahwa himpunan merupakan kumpulan
dari benda atau objek yang dapat didefinisikan dengan
jelas. Misalnya himpunan lima bilangan asli yang pertama.
Himpunan lima bilangan asli yang pertama adalah 1, 2, 3, 4,
dan 5. Suatu himpunan harus memiliki nama. Nama
himpunan biasanya ditulis dengan huruf kapital.
Contoh:
A = himpunan 5 bilangan asli yang pertama.
Nama himpunan menggunakan huruf kapital.

21. Himpunan A adalah himpunan 5 bilangan asli yang
pertama yaitu 1, 2, 3, 4, dan 5. Bilangan 1, 2, 3, 4,
dan 5 disebut anggota dari himpunan A.
Anggota himpunan biasanya dinotasikan dengan ∈.
Contoh:
1 ∈ A dibaca satu merupakan anggota dari
himpunan A.
2 ∈ A dibaca dua merupakan anggota

22. Untuk menyatakan sesuatu bukan anggota himpunan
biasanya dinotasikan dengan ∉.
Contoh:
7 ∉ A dibaca tujuh bukan anggota dari himpunan A.
9 ∉ A dibaca sembilan bukan anggota dari himpunan A.
Anggota suatu himpunan dinotasikan dengan ∈.
Bukan anggota suatu himpunan dinotasikan dengan
∉.
Himpunan A adalah himpunan lima bilangan asli yang pertama
yaitu 1, 2, 3, 4, dan 5. Banyaknya anggota himpunan A adalah
5. Notasi banyaknya anggota himpunan A dapat ditulis n(A) = 5
dibaca banyaknya anggota himpunan A adalah 5.

23. Cara Menentukan Himpunan
Ada 3 cara untuk menyatakan himpunan
yaitu :
1. Menyatakan dengan kata-kata
2. Mendaftar (tabulasi)
3. Notasi pembentuk himpunan

24. 1. Menyatakan dengan kata-kata
• Contoh :
1. Untuk menyatakan a, b, c, d, dan e sebagai
himpunan dengan kata-kata adalah …
A = himpunan lima abjad pertama
2. Untuk menuliskan 1, 2, 3, 4, dan 5 sebagai
himpunan dengan kata-kata adalah …
B = himpunan bilangan asli yang kurang dari 6

25. • Contoh :
1. A = {2, 3, 5, 7, 9}
2. M = {Bandung, Jakarta, Semarang, Surabaya}
3. S = {Senin, Selasa, Sabtu}
4. C = {1, 2, 3, 4, …}
2. Mendaftar (tabulasi)

26. Mendaftar (tabulasi)
• Hal yang harus diperhatikan dalam menyatakan
himpunan dengan cara mendaftar, yaitu sebagai
berikut :
1. Anggota suatu himpunan yang muncul lebih dari
satu kali, cukup ditulis sekali saja
2. Penulisan anggota himpunan boleh
mengabaikan urutannya
3. Untuk himpunan yang jumlah anggotannya tak
berhingga dan anggotannya mempunyai urutan
tertentu dapat menggunakan tiga titik (…)

27. • Contoh :
1. H adalah himpunan nama bulan yang diawali
dengan huruf J
H = {x| x , nama bulan yang diawali dengan
huruf J }
Penotasian tersebut dibaca sebagai
himpunan H dengan x nama bulan yang
diawali dengan huruf J
3. Notasi pembentuk himpunan

28. • Contoh :
2. A = {1, 2, 3, 4, 5}
A = {x| x < 6, x bilangan asli }
Penotasian tersebut dibaca sebagai
himpunan A dengan x kurang dari 6 dan x
anggota bilangan asli
Notasi pembentuk himpunan

29. • Himpunan berhingga adalah : himpunan yang
semua anggotanya diketahui, sedangkan
himpunan tak berhingga adalah himpunan
yang anggotanya tak terbatas.
Contoh :
1. A = {1, 2, 3, 4}
Banyak anggota A adalah 4 yaitu 1, 2, 3, dan 4
sehingga banyak anggota A dapat ditulis
n(A)=4, jadi A adalah himpunan berhingga
Himpunan Berhingga dan Tak
berhingga

30. Contoh :
2. B = {2, 3, 5, 7, …}
Banyak anggota himpunan B tidak dapat
diketahui, sehingga kita tidak dapat
menyebutkan berapa banyak anggota B, jadi
himpunan B merupakan himpunan tak
berhingga.
Himpunan Berhingga dan Tak
berhingga

31. • Himpunan kosong adalah : himpunan yang
tidak mempunyai anggota.
• Lambangnya: O atau
• Contoh :
1. Himpunan bilangan asli yang kurang dari 1
2. Himpunan manusia yang pernah tinggal di
matahari
Himpunan Kosong
 

32. Contoh :
3.
4.
Himpunan Kosong
 primabilanganxxxA  ,2
 101,62  yyyP

33. Himpunan di dalam himpunan yang lain
Lambangnya
Ada 3 buah himpunan yaitu A, B dan C yang
didefinisikan sebagai berikut :
A = {0, 1, 2, 3, 4, 5}
B = {1, 2, 3}
C = {6, 7, 8}
Himpunan Bagian
bagianhimpunan

34. • Perhatikan himpunan A dan B
Semua anggota B adalah anggota A, maka B
merupakan bagian dari A dengan kata lain
himpunan B merupakan himpunan bagian dari
himpunan A , sehingga kita dapat menuliskan
“ “ dibaca (himpunan B merupakan
himpunan bagian dari himpunan A )
Himpunan Bagian
AB 

35. • Perhatikan himpunan A dan C
A = {0, 1, 2, 3, 4, 5}
B = {1, 2, 3}
C = {6, 7, 8}
Himpunan C bukan merupakan himpunan
bagian dari A atau “ “
Himpunan Bagian
AC 

36. • Memuat seluruh anggota yang di bicarakan
• Di dalamnya ada himpunan lain
• Dilambangkan S atau U
Contoh :
A = {3, 4, 5} : Himpunan semesta yang
mungkin dari A antara lain :
Himpunan Semesta

37. Jawab :
1. S = {1, 2, 3, 4, 5}
2. S = {2, 3, 4, 5}
3. S = himpunan bilangan asli
4. S = himpunan bilangan cacah
Himpunan Semesta

38. • Untuk memahami banyaknya himpunan
bagian, mengenal dulu sifat-sifat berikut:
1. Suatu himpunan merupakan himpunan
bagian dari himpunan itu sendiri
2. Himpunan kosong merupakan himpunan
bagian dari stiap himpunan
Rumus : 2 𝑛
** n = banyaknya anggota
himpunan
Banyaknya Himpunan Bagian

39. Contoh :
Dengan sifat-sifat di atas tentukan banyaknya
himpunan bagian dari :
a. A = {a}
b. B = {a, i}
c. C = {a, I, e}
Banyaknya Himpunan Bagian

40. Contoh :
Dengan sifat-sifat di atas tentukan banyaknya
himpunan bagian dari :
a. A = {a}
Banyaknya himpunan bagian dari A = {a}
adalah 2, yaitu : { } dan {a}
Banyaknya Himpunan Bagian

41. Contoh :
Dengan sifat-sifat di atas tentukan banyaknya
himpunan bagian dari :
a. B = {a, i}
Banyaknya himpunan bagian dari B = {a, i}
adalah 4, yaitu : { } ,{a} , {i} , {a,i}
Banyaknya Himpunan Bagian

42. Contoh :
Dengan sifat-sifat di atas tentukan banyaknya
himpunan bagian dari :
a. C = {a, i, e}
Banyaknya himpunan bagian dari C = {a, i, e}
adalah 8 , yaitu : { } ,{a} , {i} , {e} , {a,i}, {a,e} ,
{i,e} dan {a,i,e}
Banyaknya Himpunan Bagian

43. n(P) Banyaknya Himpunan
Bagian
Rumus
1 2 2 𝟏
2 4 22
3 8 23
4 ... …
5 … …
6 … …
Banyaknya Himpunan Bagian

44. Himpunan dapat dinyatakan dalam bentuk gambar yang dikenal
sebagai Diagram Venn.
Hal-hal yang perlu diperhatikan dalam membuat diagram Venn
yaitu:
Himpunan semesta (S) digambarkan sebagai persegi panjang
dan huruf S diletakkan di sudut kiri atas persegi panjang
Setiap himpunan yang dibicarakan (selain himpunan kosong)
ditunjukkan oleh kurva/lingkaran.
Setiap anggota ditunjukkan dengan noktah (titik)
Bila anggota suatu himpunan banyak sekali, maka anggota-
anggotanya tidak perlu dituliskan.
DIAGRAM VENN

45. Diagram Venn
• Diagram Venn pertama kali dikenal oleh
seorang matematikawan Inggris yang
bernama Jhon Venn (1834-1923)
Contoh :
1. S = {1, 2, 3, 4, 5, 6}
A = {2, 3, 4}
B = {4, 5}
S ●6
●2
●5
●3
●4
●1
A B

46. Diagram Venn
Contoh :
1. S = {A = {x| x bilangan asli }
A = {2, 3, 4}
B = {1, 5, 6}
S
●6
●2 ●5
●3●4 ●1
A B

47. Irisan dua himpunan A dan B adalah
himpunan semua objek atau anggota
himpunan yang sekaligus menjadi
anggota himpunan A dan B. Adapun
bentuk umum irisan adalah :
A ∩ B = {x|x ϵ A atau x ϵ B}
Irisan Dua Himpunan

48. Irisan Dua Himpunan
Contoh:
A = {a, i, e}
B = {a, e, i} S
●a
●i
●e
A = B
S
Jadi : A  B= {a, i, e}

49. Irisan Dua Himpunan
Contoh:
A = {a, i, e, o}
B = {i, e} S
●e●i
A
B
●a
●o
Jadi : A  B= {i, e}

50. Irisan Dua Himpunan
Contoh:
A = {a, i, e}
B = {i, e, o} S
●e
●i
A B
●a ●oJadi : A  B= {i, e}

51. Gabungan Dua Himpunan
Gabungan dua himpunan A dan B adalah
semua objek yang merupakan anggota A
dan B. Adapun bentuk umum dari
Gabungan adalah :
A ∪ B = {x|x ϵ A atau x ϵ B}

52. Gabungan Dua Himpunan
Contoh :
S
●3
●4
A B
●1 ●5
Jadi : A ∪ B= {1, 2, 3, 4, 5, 6}
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
●6
●2

53. Gabungan Dua Himpunan
Jadi : A ∪ B= {1, 2, 3, 4,}
A = {1, 2, 3, 4}
B = {1, 2, 3, 4}
Contoh :
S
●1 ●2
●3 A = B
S
●4

54. Gabungan Dua Himpunan
Jadi : A ∪ B= {1, 2, 3, 4, 5, 6}
A = {1, 2, 3, 4, 5, 6}
B = {1, 2}
Contoh :
S
●2●1
A
B
●3
●4
●5
●6

55. Gabungan Dua Himpunan
Jadi : A ∪ B= {1, 2, 3, 4, 5, 6}
A = {1, 2, 3, 4}
B = {5,6}
Contoh :
S
●6
●2 ●5
●3●4
●1
A B