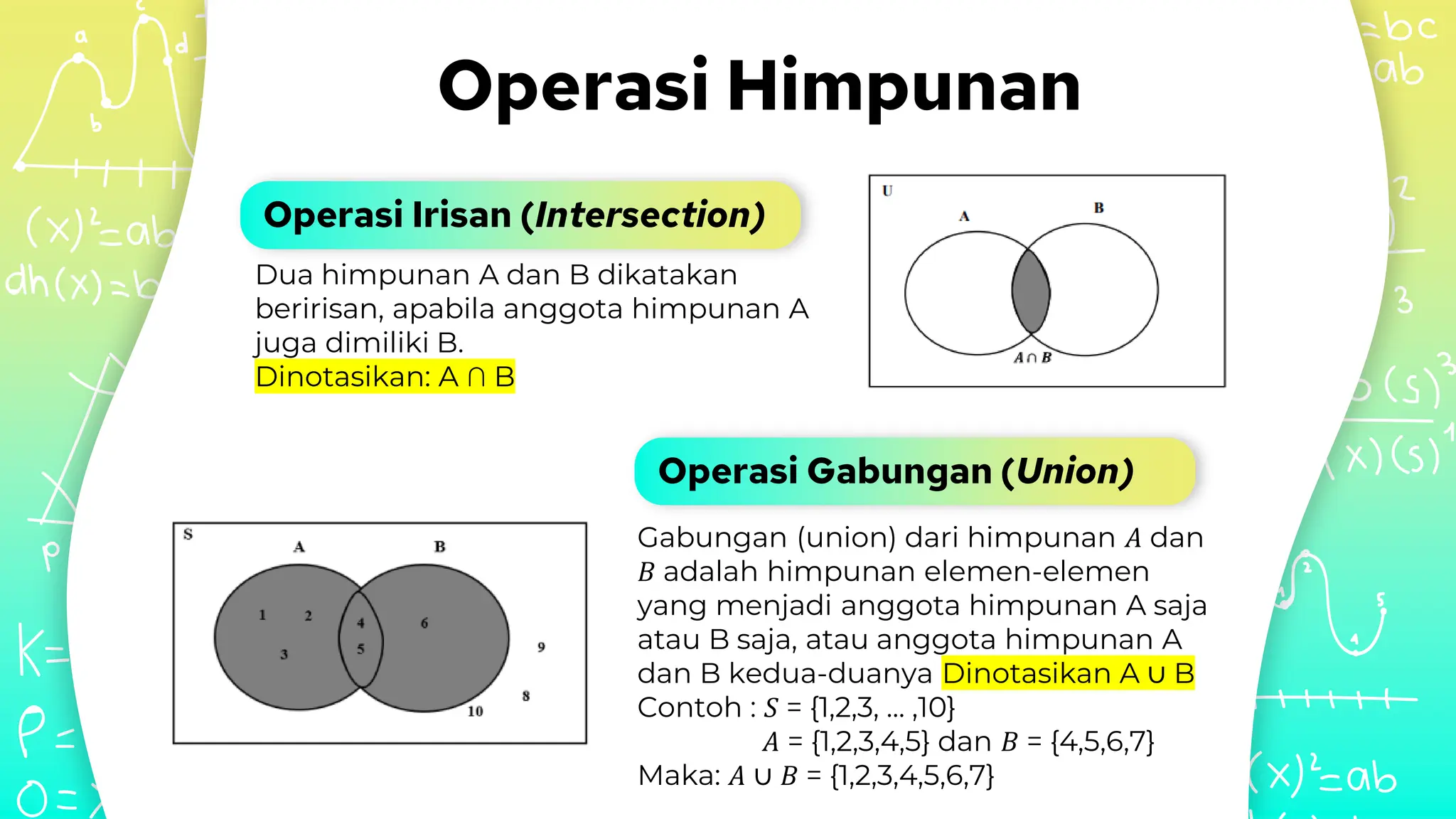
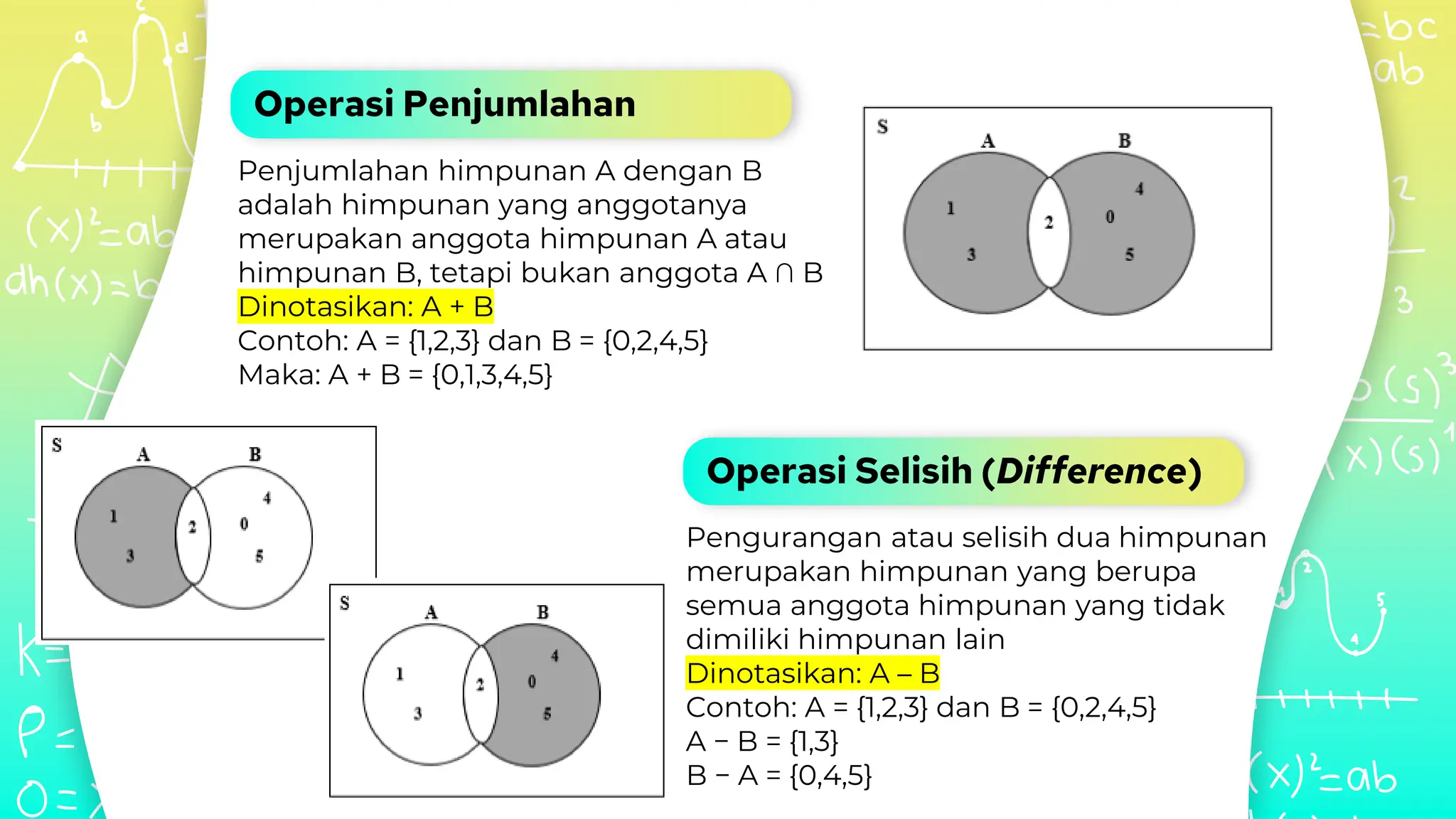
Dokumen ini membahas konsep dasar himpunan dalam matematika, termasuk definisi, notasi, dan jenis-jenis himpunan seperti himpunan bagian, himpunan kosong, dan himpunan semesta. Selain itu, dijelaskan juga tentang operasi pada himpunan seperti irisan, gabungan, selisih, dan komplemen, serta penerapan konsep himpunan dalam ilmu farmasi. Contoh soal juga diberikan untuk menjelaskan penerapan praktis dari konsep-konsep ini.

1. Matematika
HIMPUNAN
Kelompok 4
Annisa Amalia Amanah Gappa 52023011093
Indira Juliana Agatha Rande 51923011088

2. Konsep Dasar Himpunan
“Himpunan adalah sekumpulan objek
yang mempunyai syarat tertentu dan
jelas” – Georg Cantor (1918)
Objek yang dimaksud dapat berupa bilangan, manusia,
hewan, tumbuhan dan sebagainya yang selanjutnya disebut sebagai
elemen atau anggota suatu himpunan.
Syarat tertentu dan jelas dalam menentukan anggota
suatu himpunan ini sangat penting karena untuk membedakan
mana yang menjadi anggota himpunan dan mana yang bukan
merupakan anggota himpunan. Inilah yang kemudian
dinamakan himpunan terdefinisi dengan baik (well-defined set).

3. Notasi Himpunan
Himpunan biasanya dinyatakan dengan huruf besar A, B, C,
H, K dan sebagainya. Untuk menyatakan suatu himpunan digunakan
simbol “{….}”. Sementara itu untuk melambangkan anggota himpunan
biasanya menggunakan huruf kecil a, b, c, x, y dan sebagainya.
Perlu diperhatikan bahwa penulisan anggota dalam suatu
himpunan hanya sekali saja. Untuk menyatakan anggota suatu
himpunan digunakan lambang “∈” (dibaca: anggota) sedangkan untuk
menyatakan bukan anggota suatu himpunan digunakan lambang “∉”
(dibaca: bukan anggota).

4. Enumerasi
Yaitu dengan cara menuliskan semua elemen himpunan yang bersangkutan di antara dua
buah kurung kurawal.
Contoh :
Himpunan A yang berisi empat buah bilangan asli pertama ditulis sebagai A = {1,2,3,4}
Penyajian Himpunan
01
Simbol Baku
Terdapat sejumlah simbol baku yang biasanya digunakan untuk mendefinisikan himpunan
yang sering digunakan, yaitu :
P = himpunan bilangan bulat positif
N = himpunan bilangan asli
Z = himpunan bilangan bulat
Q = himpunan bilangan rasional
R = himpunan bilangan real
C = himpunan bilangan kompleks
02

5. Notasi Pembentuk Himpunan
Penyajian Himpunan
03
Himpunan dinyatakan dengan menulis syarat
yang harus dipenuhi oleh anggotanya.
Contoh :
A adalah himpunan bilangan bulat positif yang
kecil dari 5, dinyatakan sebagai
A = {x | x adalah himpunan bialngan bulat positif
yang lebih kecil dari 5}
A = {x | x ∈ P, x < 5} = {1,2,3,4}
Diagram Venn
04
Diagram Venn menyajikan himpunan
secara grafis. dalam diagram Venn
himpunan semesta U digambarkan sebagai
suatu segi empat sedangkan himpunan
lainnya digambarkan sebagai lingkaran di
dalam segi empat tersebut.
Contoh :
U = {1,2,…,7,8}, A = {1,2,3,5} dan B =
{2,5,6,8} Ketiga himpunan tersebut
digambarkan dengan diagram Venn pada
gambar berikut :

6. Jenis-jenis Himpunan
Himpunan A dikatakan himpunan bagian (subset dari himpunan B jika dan hanya
setiap unsur A merupakan unsur dari B. dalam hal ini, B dikatakan superset dari A.
Notasinya: A ⊄ B atau A ⊂ B
Himpunan Bagian
Jika suatu himpunan tidak mempunyai elemen, dengan kata lain dengan kardinalitas
himpunan tersebut sama dengan nol maka himpunan tersebut dinamakan himpunan
kosong (null set).
Notasinya: Ø atau { }
Himpunan Kosong
Himpunan Semesta
Yaitu himpunan yang elemenya semua objek pembicaraan. Himpunan semesta
dilambangkan dengan S atau U.
Contoh: Jika U = {1, 2, 3, 4, 5} sebagai semesta pembicaraan dan
A = {1, 3, 5} maka dikatakan bahwa A merupakan himpunan bagian dari U

7. Dua buah himpunan dikatakan ekivalen jika masing-masing mempunyai kardinalitas
yang sama. Misalkan, himpunan A adalah ekivalen dengan himpunan B berarti kardinal
dari himpunan A dan himpunan B adalah sama.
Notasinya: A ~ B
Himpunan Ekivalen
2 himpunan A dan B diakatakan saling lepas (disjoint) jika keduanya tidak memiliki usur
yang sama atau dua himpunan dikatakan saling lepas bila irisannya adalah himpunan
kosong.
Notasinya: A // B
Himpunan Disjoint / saling lepas
Himpunan Berhingga & tak Berhingga (Infinit)
Himpunan diakatakan berhingga jika ia mempunyai elemen yang banyaknya
berhingga. Begitujuga sebaliknya dengan himpunan tak berhingga..

8. Operasi Himpunan
Operasi Irisan (Intersection)
Dua himpunan A dan B dikatakan
beririsan, apabila anggota himpunan A
juga dimiliki B.
Dinotasikan: A ∩ B
Operasi Gabungan (Union)
Gabungan (union) dari himpunan 𝐴 dan
𝐵 adalah himpunan elemen-elemen
yang menjadi anggota himpunan A saja
atau B saja, atau anggota himpunan A
dan B kedua-duanya Dinotasikan A ∪ B
Contoh : 𝑆 = {1,2,3, … ,10}
𝐴 = {1,2,3,4,5} dan 𝐵 = {4,5,6,7}
Maka: 𝐴 ∪ 𝐵 = {1,2,3,4,5,6,7}

9. Operasi Penjumlahan
Penjumlahan himpunan A dengan B
adalah himpunan yang anggotanya
merupakan anggota himpunan A atau
himpunan B, tetapi bukan anggota A ∩ B
Dinotasikan: A + B
Contoh: A = {1,2,3} dan B = {0,2,4,5}
Maka: A + B = {0,1,3,4,5}
Operasi Selisih (Difference)
Pengurangan atau selisih dua himpunan
merupakan himpunan yang berupa
semua anggota himpunan yang tidak
dimiliki himpunan lain
Dinotasikan: A – B
Contoh: A = {1,2,3} dan B = {0,2,4,5}
A − B = {1,3}
B − A = {0,4,5}

10. Operasi Komplemen
Komplemen dari himpunan A didefinisikan semua anggota himpunan semesta
yang bukan anggota himpunan A.
Dinotasikan: A′ atau A𝑐 (“A aksen” atau “A komplemen”)
Contoh: 𝑆 = { 1,2,3,4,5,6,7,8,9,10 } dan A = { 1, 2, 3, 4, 5,}
Maka: A𝑐 = {6,7,8,9,10}.
Operasi Perkalian
Operasi perkalian himpunan A dan B adalah hasil himpunan barunya
merupakan semua pasangan berurut yang dibentuk dari anggota-anggota
himpunan A dan B
Dinotasikan: 𝐴 × 𝐵 = {(𝐴, 𝐵)|𝑎 ∈ 𝐴 dan 𝑏 ∈ 𝐵}
Contoh: A= {1, 2, 3} dan B = {a, b}
Maka,
𝐴 × 𝐵 = {(1, 𝑎), (1, 𝑏), (2, 𝑎), (2, 𝑏), (3, 𝑎), (3, 𝑏)}
𝐵 × 𝐴 = {(𝑎, 1), (𝑏, 1), (𝑎, 2), (𝑏, 2), (𝑎, 3), (𝑏, 3)}

11. Operasi Beda Setangkup (Symmetric Difference)
Beda setangkup antara dua buah himpunan merupakan suatu
himpunan yang anggotanya ada pada himpunan A dan B, tetapi tidak
pada keduanya.
Notasi: A ⊕ B
Contoh:
𝐴 dan 𝐵 adalah himpunan, maka beda setangkup antara 𝐴 dan 𝐵 adalah:
𝐴 ⊕ 𝐵 = (𝐴 ∪ 𝐵) − (𝐴 ∩ 𝐵)
atau
𝐴 ⊕ 𝐵 = (𝐴 − 𝐵) ∪ (𝐵 − 𝐴)

12. Contoh Soal 1
Diketahui:
P = {7, 11, 13, 17, 19, 23}
Q = {5, 7, 9, 11, 13}
Maka tentukanlah anggota dari A ∩ B?
Pembahasan :
A ∩ B merupakan himpunan yang
anggotanya merupakan anggota P
sekaligus merupakan anggota Q,
maka: A ∩ B = {7, 11, 13}

13. Contoh Soal 2
Suatu kelas terdiri dari 40 orang siswa, dan diantaranya ada 15 orang siswa yang menyukai
pelajaran matematika, lalu ada 13 orang siswa yang menyukai pelajaran bahasa inggris dan yang
7 orang siswa yang menyukai keduanya.
Berapa banyak siswa yang tidak menyukai pelajaran matematika maupun bahasa inggris ?
Pembahasan:
Misal
x = banyak siswa yang tidak menyukai kedua pelajaran.
Maka:
Banyak siswa yang hanya menyukai matematika adalah 15 – 7 =
8 orang siswa.
Banyak siswa yang hanya menyukai bahasa inggris adalah 13 – 7
= 6 orang siswa.
Himpunan tersebut bisa digambarkan dengan diagram venn
sebagai berikut:
Banyak anak yang tidak menyukai kedua pelajaran ialah :
40 = 8 + 7 + 6 + x
40 = 21 + x
x = 40 – 21
x = 19
Jadi, banyak siswa yang tidak menyukai pelajaran matematika
maupun bahasa inggris adalah 19 orang.

14. Implementasi
Konsep Himpunan
dalam Ilmu Farmasi
• Metode perencanaan dan pengendalian
obat dengan analisis ABC & VEN
• Metode penyimpanan obat
a) Berdasarkan abjad
b) Berdasarkan generic dan Non-generic
c) Berdasarkan kelas terapi
d) Berdasarkan bentuk sediaan
e) Berdasarkan stabilitas obat
f) Berdasarkan undang-undang