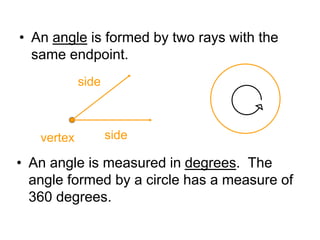
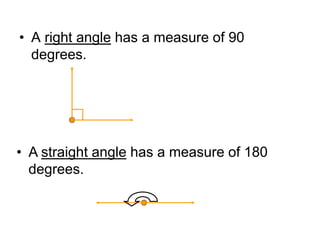
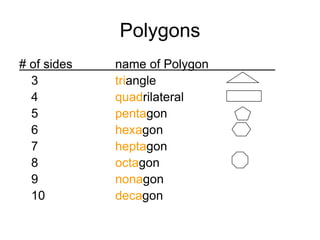
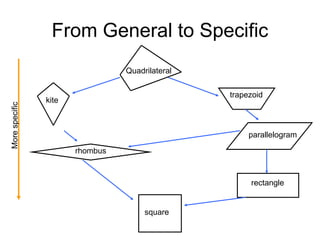
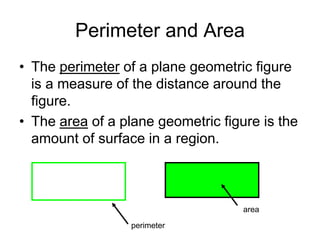
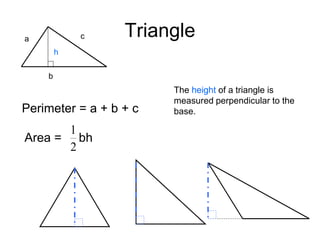
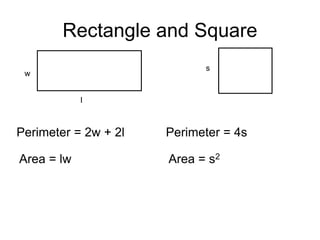
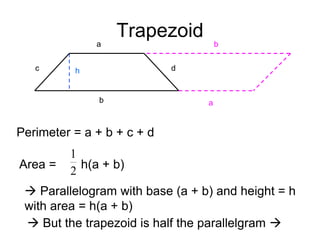
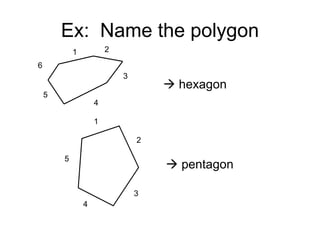
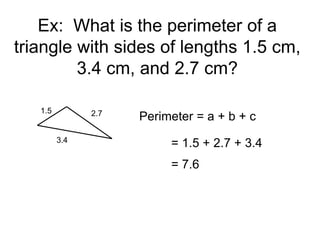
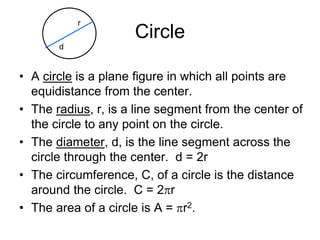
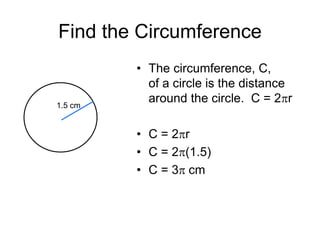
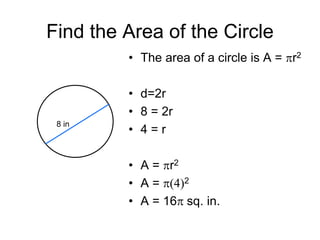
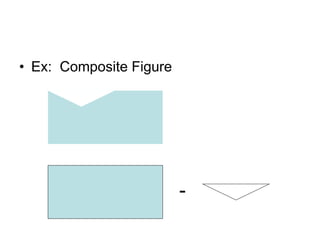
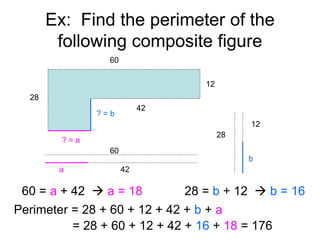
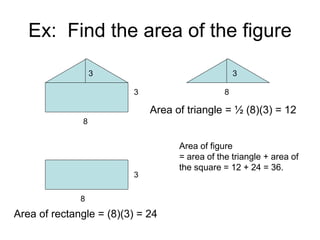
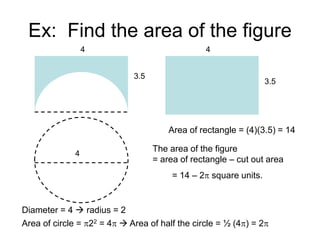
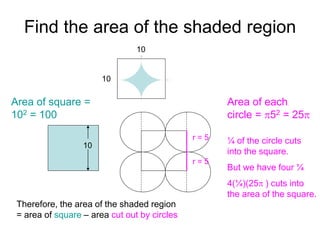
This document provides an introduction to geometry. It begins by defining geometry as the study of shapes and notes it is one of the oldest branches of mathematics. It discusses how modern geometry began with the Greeks over 2000 years ago and how Euclid of Alexandria wrote "The Elements", systematically recording all known geometry. Basic geometric terms like points, lines, planes, angles, and polygons are defined. Different types of polygons and quadrilaterals are classified. Methods for finding the perimeter and area of basic shapes like triangles, rectangles, parallelograms, trapezoids, and circles are presented. Composite figures made of multiple shapes are introduced. Several examples of calculating perimeters and areas are worked through.

1. INTRODUCTION TO
GEOMETRY
MSJC ~ San Jacinto Campus
Math Center Workshop Series
Janice Levasseur

2. Geometry
• The word geometry comes from Greek
words meaning “to measure the Earth”
• Basically, Geometry is the study of shapes
and is one of the oldest branches of
mathematics

3. The Greeks and Euclid
• Our modern understanding of geometry
began with the Greeks over 2000 years
ago.
• The Greeks felt the need to go beyond
merely knowing certain facts to being able
to prove why they were true.
• Around 350 B.C., Euclid of Alexandria
wrote The Elements, in which he recorded
systematically all that was known about
Geometry at that time.

4. The Elements
• Knowing that you can’t define everything and
that you can’t prove everything, Euclid began by
stating three undefined terms:
 Point
 (Straight) Line
 Plane (Surface)
Actually, Euclid did attempt to define these basic
terms . . .
is that which has no part
is a line that lies evenly with the points
on itself
is a plane that lies evenly with the
straight lines on itself

5. Basic Terms & Definitions
• A ray starts at a point (called the endpoint)
and extends indefinitely in one direction.
• A line segment is part of a line and has
two endpoints.
A B AB
B
A AB

6. • An angle is formed by two rays with the
same endpoint.
• An angle is measured in degrees. The
angle formed by a circle has a measure of
360 degrees.
vertex
side
side

7. • A right angle has a measure of 90
degrees.
• A straight angle has a measure of 180
degrees.

8. • A simple closed curve is a curve that we
can trace without going over any point
more than once while beginning and
ending at the same point.
• A polygon is a simple closed curve
composed of at least three line segments,
called sides. The point at which two sides
meet is called a vertex.
• A regular polygon is a polygon with sides
of equal length.

9. Polygons
# of sides name of Polygon
3 triangle
4 quadrilateral
5 pentagon
6 hexagon
7 heptagon
8 octagon
9 nonagon
10 decagon

10. Quadrilaterals
• Recall: a quadrilateral is a 4-sided polygon. We can
further classify quadrilaterals:
 A trapezoid is a quadrilateral with at least one pair of
parallel sides.
 A parallelogram is a quadrilateral in which both pairs of
opposite sides are parallel.
 A kite is a quadrilateral in which two pairs of adjacent
sides are congruent.
 A rhombus is a quadrilateral in which all sides are
congruent.
 A rectangle is a quadrilateral in which all angles are
congruent (90 degrees)
 A square is a quadrilateral in which all four sides are
congruent and all four angles are congruent.

11. From General to Specific
Quadrilateral
trapezoid
kite
parallelogram
rhombus
rectangle
square
More
specific

12. Perimeter and Area
• The perimeter of a plane geometric figure
is a measure of the distance around the
figure.
• The area of a plane geometric figure is the
amount of surface in a region.
perimeter
area

13. Triangle
h
b
a c
Perimeter = a + b + c
Area = bh
2
1
The height of a triangle is
measured perpendicular to the
base.

14. Rectangle and Square
w
l
s
Perimeter = 2w + 2l Perimeter = 4s
Area = lw Area = s2

15. Parallelogram
b
a h
Perimeter = 2a + 2b
Area = hb  Area of a parallelogram
= area of rectangle with
width = h and length = b

16. Trapezoid
c d
a
b
Perimeter = a + b + c + d
Area =
b
a
 Parallelogram with base (a + b) and height = h
with area = h(a + b)
 But the trapezoid is half the parallelgram 
h(a + b)
2
1
h

17. Ex: Name the polygon
3
2
1
4
5
6
 hexagon
1
2
3
4
5
 pentagon

18. Ex: What is the perimeter of a
triangle with sides of lengths 1.5 cm,
3.4 cm, and 2.7 cm?
1.5 2.7
3.4
Perimeter = a + b + c
= 1.5 + 2.7 + 3.4
= 7.6

19. Ex: The perimeter of a regular
pentagon is 35 inches. What is the
length of each side?
Perimeter = 5s
35 = 5s
s = 7 inches
s
Recall: a regular polygon is
one with congruent sides.

20. Ex: A parallelogram has a based
of length 3.4 cm. The height
measures 5.2 cm. What is the area
of the parallelogram?
3.4
5.2
Area = (base)(height)
Area = (3.4)(5.2)
= 17.86 cm2

21. Ex: The width of a rectangle is
12 ft. If the area is 312 ft2, what
is the length of the rectangle?
12 312 Area = (Length)(width)
L = 26 ft
Let L = Length
L
312 = (L)(12)
Check: Area = (Length)(width) = (12)(26)
= 312

22. Circle
• A circle is a plane figure in which all points are
equidistance from the center.
• The radius, r, is a line segment from the center of
the circle to any point on the circle.
• The diameter, d, is the line segment across the
circle through the center. d = 2r
• The circumference, C, of a circle is the distance
around the circle. C = 2pr
• The area of a circle is A = pr2.
r
d

23. Find the Circumference
• The circumference, C,
of a circle is the distance
around the circle. C = 2pr
• C = 2pr
• C = 2p(1.5)
• C = 3p cm
1.5 cm

24. Find the Area of the Circle
• The area of a circle is A = pr2
• d=2r
• 8 = 2r
• 4 = r
• A = pr2
• A = p(4)2
• A = 16p sq. in.
8 in

25. Composite Geometric Figures
• Composite Geometric Figures are made
from two or more geometric figures.
• Ex:
+

26. • Ex: Composite Figure
-

27. Ex: Find the perimeter of the
following composite figure
+
=
8
15
Rectangle with width = 8
and length = 15
Half a circle with diameter = 8
 radius = 4
Perimeter of composite figure = 38 + 4p.
Perimeter of partial rectangle
= 15 + 8 + 15 = 38
Circumference of half a circle
= (1/2)(2p4) = 4p.

28. Ex: Find the perimeter of the
following composite figure
28
60
42
12
? = a
? = b
60
a 42
60 = a + 42  a = 18
28
b
12
28 = b + 12  b = 16
Perimeter = 28 + 60 + 12 + 42 + b + a
= 28 + 60 + 12 + 42 + 16 + 18 = 176

29. Ex: Find the area of the figure
3
3
8
8
Area of rectangle = (8)(3) = 24
3
8
Area of triangle = ½ (8)(3) = 12
Area of figure
= area of the triangle + area of
the square = 12 + 24 = 36.
3

30. Ex: Find the area of the figure
4
3.5
4
3.5
Area of rectangle = (4)(3.5) = 14
4
Diameter = 4  radius = 2
Area of circle = p22 = 4p  Area of half the circle = ½ (4p) = 2p
The area of the figure
= area of rectangle – cut out area
= 14 – 2p square units.

31. Ex: A walkway 2 m wide surrounds
a rectangular plot of grass. The
plot is 30 m long and 20 m wide.
What is the area of the walkway?
20
30
2
What are the dimensions of the big
rectangle (grass and walkway)?
Width = 2 + 20 + 2 = 24
Length = 2 + 30 + 2 = 34
The small rectangle has area = (20)(30) = 600 m2.
What are the dimensions of the small rectangle (grass)?
Therefore, the big rectangle has area
= (24)(34) = 816 m2.
The area of the walkway is the difference between the big and small
rectangles:
20 by 30
Area = 816 – 600 = 216 m2.
2

32. Find the area of the shaded region
10
10
10
r = 5
Area of each
circle = p52 = 25p
¼ of the circle cuts
into the square.
But we have four ¼
4(¼)(25p ) cuts into
the area of the square.
Area of square =
102 = 100
Therefore, the area of the shaded region
= area of square – area cut out by circles = 100 – 25p square units
r = 5