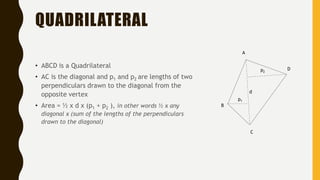
This document provides information about properties and formulas for calculating areas of various shapes: - Triangles can be categorized based on their angles (equilateral, right, isosceles). Formulas are provided to calculate their areas using measurements like altitude, legs, or side lengths. - The area of any quadrilateral can be calculated as half the product of its diagonal and the sum of the perpendiculars drawn to that diagonal. 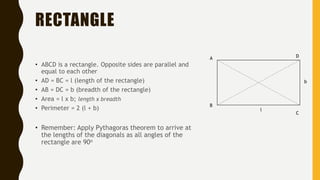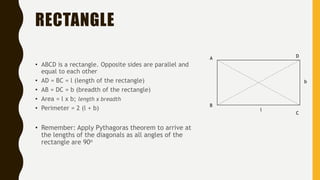- Rectangles, squares, rhombi, and trapezoids have their key properties and measurements defined, and their areas calculated using formulas involving lengths of sides or diagonals.

1. AREAS

2. TRIANGLES
• ∠A + ∠B + ∠C = 180o
• Perimeter = a + b + c = 2s
• Area = ½ (b)x (h); where b = side b which is the base
to the altitude h
Based on Heron’s Formula
• Area = 2s = √[s(s-a)(s-b)(s-c)]; where s = ½ (a+b+c)
a, b and c are three sides
of the triangle. ‘h’ is the
altitude. ∠A, ∠B and ∠C
are three angles of the
triangle

3. EQUILATERAL TRIANGLES
• All three sides have equal length
• ∠A = ∠B = ∠C = 60o
• Area = √ [¾ (a2)], where a is the length of the sides
• Altitude, h = √ [3/2 (a)]
Length of all the sides = ‘a’
A C
B
ac
b
h

4. RIGHT ANGLED TRIANGLES
• ∠A = 90o
• a2 = b2 + c2 ; Pythagoras' theorem
• Area = ½ (b) x (c); in other words ½ x product of 2 legs
∠A = 90o
A C
B
a
c
b

5. ISOSCELES TRIANGLES
• Any 2 sides of the triangle are equal
• AD = b/2 and DC = b/2, BD is perpendicular dropped
on to the base b. It divides the side AC equally.
• Since AB = BC, corresponding angles ∠A = ∠C
• Area = b/4 [√
‘a’ is the length of 2 equal sides
A
C
B
aa
b
D
(4a2 - b2) ]

6. QUADRILATERAL
• ABCD is a Quadrilateral
• AC is the diagonal and p1 and p2 are lengths of two
perpendiculars drawn to the diagonal from the
opposite vertex
• Area = ½ x d x (p1 + p2 ), in other words ½ x any
diagonal x (sum of the lengths of the perpendiculars
drawn to the diagonal)
A
B
C
D
d
p1
p2

7. RECTANGLE
• ABCD is a rectangle. Opposite sides are parallel and
equal to each other
• AD = BC = l (length of the rectangle)
• AB = DC = b (breadth of the rectangle)
• Area = l x b; length x breadth
• Perimeter = 2 (l + b)
• Remember: Apply Pythagoras theorem to arrive at
the lengths of the diagonals as all angles of the
rectangle are 90o
A
B
C
D
l
b

8. RECTANGLE
• ABCD is a rectangle. Opposite sides are parallel and
equal to each other
• AD = BC = l (length of the rectangle)
• AB = DC = b (breadth of the rectangle)
• Area = l x b; length x breadth
• Perimeter = 2 (l + b)
• Remember: Apply Pythagoras theorem to arrive at
the lengths of the diagonals as all angles of the
rectangle are 90o
A
B
C
D
l
b

9. SQUARE
• ABCD is a square. All the sides are equal and
opposite sides parallel to each other
• All angles are equal to 90o
• AB = BC = CD = DA = a ; (length of the sides)
• Area = a2
• Perimeter = 4a
• Length of the diagonal, d = a √2
A
B C
Da
d

10. RHOMBUS
• ABCD is a rhombus. All the sides are equal and opposite
sides parallel to each other
• Diagonals are not equal and bisect each other at 900
• Opposite angles are equal
• AB = BC = CD = DA = a ; (length of the sides)
• Area = a x h or 1/2 x d1 x d2
• Perimeter = 4a
• Length of the diagonal, d = a √2
• Note: Apply Pythagoras theorem at the diagonal intersection
considering the fact that they bisect each other at 900
A
B C
D
d1
d2
h
a

11. TRAPEZIUM
• ABCD is a rhombus. All the sides are equal and opposite
sides parallel to each other
• Diagonals are not equal and bisect each other at 900
• Opposite angles are equal
• AB = BC = CD = DA = a ; (length of the sides)
• Area = a x h or 1/2 x d1 x d2
• Perimeter = 4a
• Length of the diagonal, d = a √2
• Note: Apply Pythagoras theorem at the diagonal intersection
considering the fact that they bisect each other at 900
h
A
B
C
D
a
b