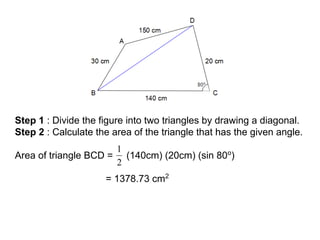
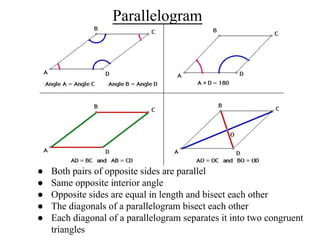
- A quadrilateral is a four-sided polygon. There are several types of quadrilaterals defined by their properties: square, rectangle, parallelogram, rhombus, trapezoid, kite, and irregular quadrilateral. - The sum of the interior angles of any quadrilateral is always 360 degrees. - Formulas are provided to calculate the perimeter and area of different quadrilaterals depending on given side lengths or angles. This includes formulas for square, rectangle, parallelogram, rhombus, trapezoid, kite, and methods described to find the area of an irregular quadrilateral by dividing it into triangles. 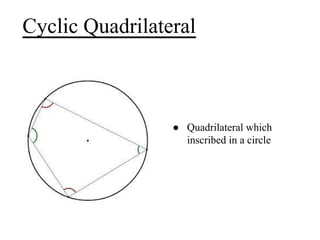- A cyclic quadrilateral has the special property

1. Quadrilateral

2. Quadrilateral
● It is a four-sided polygon with four
angles
● The sum of interior angles is 360

3. Types of Quadrilateral
Square Triangle Parallelogram
Rhombus Kite Trapezium

4. Irregular
Quadrilateral
Cyclic Quadrilateral

5. SQUARE

6. 3 cm
3 cm
1 2 3
4 5 6
7 8 9
Formula
Area = Side2
= 32
= 9cm2

7. Rectangular
The formula is:
Area = L x W
L = Length
W = Width

8. 3cm
4cm
we know
L= 4cm , W= 3cm
Area= Length x Width
= L x W
= 4 x 3
= 12cm2
12 cm2

9. Kite
● Two pairs of equal length - a & a, b & b,
are adjacent to each other
● Diagonals are perpendicular to each other
● Perimeter = 2a + 2b
● Area = ½ x d1 x d2
= ½ x DB x AC

10. Area of Kite
● Area = ½ x d1 x d2
= ½ x width x length
● The remaining parts of the rectangle can
form another kite
● So, the total area needs to be divided into
half

11. Area = ½ x d1 x d2
= ½ x 4.8 x 10
= 24cm2
Area = ½ x d1 x d2
= ½ x (4+9) x (3+3)
= 39m2

12. Find the length of the diagonal of a kite whose area is 168 cm2
and
one diagonal is 14 cm.
Solution:
Given: Area of the kite (A) = 168 cm2
and one diagonal (d1) = 14 cm.
Area of Kite = ½ x d1 x d2
168 = ½ x 14 x d2
d2 = 168/7
d2 = 24cm

13. Parallelogram
● Both pairs of opposite sides are parallel
● Same opposite interior angle
● Opposite sides are equal in length and bisect each other
● The diagonals of a parallelogram bisect each other
● Each diagonal of a parallelogram separates it into two congruent
triangles

14. Parallelogram
Perimeter = 2a + 2b
Area = base x height
= b x h
Not using
value a to
calculate area!

15. Area of Parallelogram
When adjacent lengths and included angle is given,
From Theorem Hypotenuse ,
sin a = opposite / hypotenuse
sin a = h/b
Rearrange the equation, so h = b sin a
Area of Parallelogram ABCD = base x height
= a x b sin a
= ab sin a

16. Example : Area of parallelogram
Find the area of a parallelogram, two adjacent sides of which are 17cm
and 20cm and their included angle is 60 degree.
Solution :
Area of parallelogram = ab sin θ
= (17)(20) sin 60
= 340cm2
x 0.866
= 294.44cm2

17. Rhombus
● Four equal length , A=B=C=D
● Diagonals are unequal , bisect and
perpendicular to each other
● Perimeter = A+B+C+D
● Area - Altitude x Base
- a2
sin θ
- (½) ( d1
x d2
)

18. How area formula of Rhombus developed?
● Area = Altitude x Base
● Same as the area formula of a square

19. How area formula of Rhombus developed?
Diagonal AC divides the rhombus into two equal triangle ,
therefore the formula of the rhombus is given as :
Area of the rhombus = 2 x (½) ( a x a sin θ )
= a2
sin θ

20. Example : Area of rhombus
The side of a rhombus is 120m and two opposite angles are
60 degree each. Find the area.
Solution :
Area of rhombus = a2
sin θ
= (120)(120) sin 60
= 14400m2
x 0.866
= 12470.4m2

21. How area formula of Rhombus developed?
Diagonal AC & BD divide the rhombus into four equal triangles,
therefore area of rhombus given as :
Area of rhombus = 4 x ( ½ ) x ( AC/2 ) x ( BD/2 )
= ½ ( AC x BD )
= ½ ( d1
x d2
)

22. Example : Area of rhombus
The diagonal of a rhombus are 20m and 10m. Find its area.
Solution :
Area of rhombus = ½ ( d1
x d2
)
= ½ ( 20m x 10m )
= ½ ( 200m2
)
= 100m2

23. Trapezium
● 2-dimensional geometric figure with four sides
● at least one set of sides are parallel
● parallel sides are called the bases,
● other sides are called the legs

24. Properties of Trapezium
1)Perimeter of trapezium
Perimeter= a+b+c+d

25. 2) Area of Trapezium
Area=½ x h x (a+b)

26. Derivation of the formula of trapezium
Area of Parallelogram= Base x Height
=(b1+b2) x h
Since this is the area of two trapezium we have to divide this by
two, giving
Area of Trapezium=½ (b1+ b2) x h

27. Example:
Find the area of a trapezoid with bases of 9 centimeters and 7
centimeters, and a height of 3 centimeters.
Solution:
Area = ½ x base x height
= ½ x (9 cm + 7 cm) x 3 cm
= ½ x (16 cm) x (3 cm)
= ½ x 48 cm2
= 24 cm2

28. Cyclic Quadrilateral
● Quadrilateral which
inscribed in a circle

29. Properties of Cyclic
Quadrilateral
● Corresponding angle ● External angle
Since ∠ABC+∠ADC=180°,
∠ABC= ∠ADE

30. Area of
Cyclic Quadrilateral
The Brahmagupta’s
Formula:
where s = half perimeter of
quadrilateral

31. How Does the Brahmagupta’s
Formula Derived?
By extending line AB and line DC,
intersection point P is formed.
From the properties of cyclic
quadrilateral, ∠ABC= ∠ADP and
∠BCD= ∠PAD.
Therefore, ΔPBC is similar to ΔPAD.
The ratio of the two triangles:

32. How Does the Brahmagupta’s
Formula Derived?

33. How Does the Brahmagupta’s
Formula Derived?
Proof of Heron’s Formula:
http://jwilson.coe.uga.
edu/emt725/Heron/HeronProofAlg.html

34. How Does the Brahmagupta’s
Formula Derived?

35. How Does the Brahmagupta’s
Formula Derived?

36. Then, find s by substitute e
and f.

37. Then evaluate [s-(e+a)], [s-
(f+c)] and (s-b) in terms of
a,b, c and d
You will find that
[s-(e+a)]
[s-(f+c)] (s-b)

38. Finally, evaluate the Area of Cyclic Quadrilateral
Therefore,

39. Example:
Problem 1: Find the area of a cyclic quadrilateral whose sides are 7 cm, 5 cm, 4
cm and 10 cm.
Solution: Given that a = 7 cm, b = 5 cm, c = 4 cm and d = 10 cm
s = (7+5+4+10)/2
s = 13
Using Brahmagupta's formula:
Area of cyclic quadrilateral = √(s−a)(s−b)(s−c)(s−d)
= √(13−7)(13−5)(13−4)(13−10)
= √(6)(8)(9)(3)
= √1296

40. Problem 2: Find the area of a cyclic quadrilateral with sides 1 m, 300 cm, 2 m
and 1.2 m.
Example:
Solution: Given that a =100 cm, b =300 cm, c =200 cm and d = 120 cm
s = (100+300+200+120)/2
s = 360 cm
Using Brahmagupta's formula:
Area of cyclic quadrilateral = √(s−a)(s−b)(s−c)(s−d)
=√(360−100)(360−300)(360−200)(360−120)
= √(260)(60)(160)(240)
= √599040000
= 224475.3 sq cm
= 22.448 sq m

41. Irregular Quadrilateral
• Quadrilateral that does not fit into any of
the above is considered as irregular
quadrilateral.

42. Steps to find the area of an irregular
quadrilateral
Examples
Find the area of a quadrilateral ABCD where AB = 30cm, BC = 140cm,
CD = 20cm and DA = 150cm.
B C
A
D
140 cm
150 cm
30 cm 20 cm

43. Step 1 : Divide the figure into two triangles by drawing a diagonal.
Step 2 : Calculate the area of the triangle that has the given angle.
Area of triangle BCD = (140cm) (20cm) (sin 80o
)
= 1378.73 cm2

44. Step 3 : Calculate the length of the diagonal BD using the Law of Cosines.
BD2
= 1402
+ 202
- 2(140)(20) cos 80o
BD = 137.94 cm

45. Step 5 : Calculate the area of the second triangle using Heron's Formula.
Perimeter of triangle ABD = 30 cm + 150 cm + 137.94 cm
= 317.94 cm
Half of the perimeter, s = 158.97 cm
Area of triangle ABD =
= 1966.61 cm2

46. 1966.61 cm2
Step 6 : Add the two areas of the triangles to determine the area of the
quadrilateral.
Area of Quadrilateral ABCD
= Area of triangle ABD + Area of triangle BCD
= 1966.61 cm2
+ 1378.73 cm2
= 3345.34 cm2