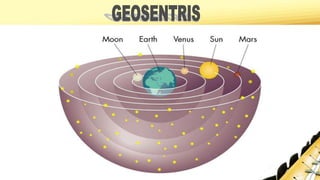
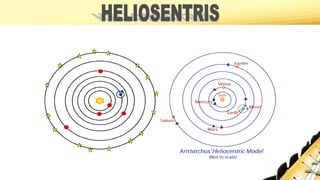
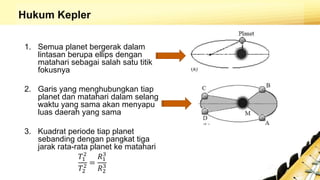
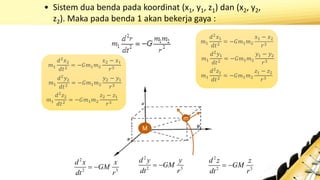
Dokumen tersebut membahas tentang perkembangan teori geosentris dan heliosentris dalam astronomi, mulai dari pandangan Yunani Kuno hingga penemuan hukum gravitasi dan gerakan planet oleh Newton. Dokumen ini juga menjelaskan kontribusi ilmuwan seperti Copernicus, Kepler, Galileo, dan Newton dalam mengembangkan pemahaman tentang sistem tata surya dan hukum gravitasi universal.

1. GRAVITASI UNIVERSAL
1. Nanda Paranty Azhary (4201414005)
2. Ika Nirvaana (42014140100)
3. Diyah Ayu Budi L (4201414027)
4. Yoga Ahmadi (4201414061)
5. Zahrina Lu’aili (4201414091)

2. Perkembangan Teori Geosentris
• Astronomi sebagai ilmu baru berkembang di Yunani pada abad IV SM yang
berpendapat bahwa bumi berbentuk datar.
• Dua abad kemudian muncul terobosan pertama dalam astronomi yang
dilakukan oleh Aristoteles yang berpendapat bahwa bumi bulat bundar.
• Zaman astronomi klasik Yunani ditutup oleh Hipparchus pada abad I SM
yang menyatakan bumi yang bundar itu diam. Matahari, bulan dan planet-
planet lain mengelilingi bumi dalam lintasan yang lebih rumit yang terdiri dari
lingkaran-lingkaran kecil dinamakan epicycle yang menumpangi lingkaran-
lingkaran yang lebih besar.
• Sistem geosentris ini disempurnakan oleh Cladius Ptolemaus pada abad II M
yang merupakan ilmuwan astronomi Mesir Kuno. Sistem geosentris ini
disebut juga teori geosentris atau lebih dikenal sistem Ptolemaus.

4. Perkembangan Teori Heliosentris
• Lebih dari tiga belas abad toeri geosentris diterima masyarakat dunia. Barulah pada
tahun 1512, seorang ilmuwan astronomi berkebangsaan Polandia, Nicolaus
Copernicus (1473-1543) mengemukakan bahwa benda langit mengelilingi matahari
dengan orbit lingkaran.
• Pernyataan ini mendukung pernyataan Aristacus yang sebelumnya telah
mengatakan bahwa mataharilah pusat tata surya. Sistem ini disebut sistem
heliosentris (bahasa Yunani : Helios = matahari).
• Dalam sistem Copernicus gerak benda langit tampak menjadi lebih sederhana dan
memudahkan pengelompokkan keluarga benada langit secara bersistem. Dalam
pandangan ini para ilmuwan kemudian mengemukakan apa yang dikenal dengan
sistem tata surya, yaitu kelompok atau keluarga benda langit yang bergerak
mengelilingi matahari.

5. • Adanya dua teori yang bertentangan tersebut telah merangsang para
ahli ilmu hitung untuk memperoleh data pengamatan yang lebih teliti.
Data seperti itu akhirnya didapat oleh Tycho Brache. Namun dalam
melakukan pengamatan, Brache belum menggunakan teleskop.
• Pada tahun 1609, Kepler mendukung gagasan teori heliosentris dengan
mengeluarkan tiga hukumnya yang selain menyebutkan bahwa matahari
adalah pusat tata surya juga memperbaiki mengenai bentuk orbit planet,
yaitu yang berbentuk ellips.
• Pada tahun yang sama, Galileo menjadi penemu teleskop yang
pertama. Melalui pengamatan dengan menggunakan teleskopnya,
Galileo menyimpulkan bahwa bumi bukanlah pusat gerak. Penemuan
teleskop oleh Galileo ini bukan saja membantu menguatkan konsep
heliosentris Copernicus tetapi juga membuka lembaran baru dalam
perkembangan ilmu astronomi selanjutnya.

7. Hukum Kepler
• Orang Yunani Kuno menganggap benda langit bergerak dalam
lintasan yang berupa lingkaran.
• Akhir abad XVI, Tycho Brache mempelajari tentang gerakan
planet dan menerbitkan buku.
• Johanes Kepler, mengemukakan bahwa
1. orbit planet mengelilingi matahari tidaklah berbentuk lingkaran
melainkan berbentuk ellips
2. 𝑣 𝑝𝑙𝑎𝑛𝑒𝑡 semakin besar saat mendekati matahari
3. Terdapat hubungan antara periode planet dan jarak rata-ratanya
dari matahari

8. Hukum Kepler
1. Semua planet bergerak dalam
lintasan berupa ellips dengan
matahari sebagai salah satu titik
fokusnya
2. Garis yang menghubungkan tiap
planet dan matahari dalam selang
waktu yang sama akan menyapu
luas daerah yang sama
3. Kuadrat periode tiap planet
sebanding dengan pangkat tiga
jarak rata-rata planet ke matahari
𝑇1
2
𝑇2
2 =
𝑅1
3
𝑅2
3

9. HUKUM GRAVITASI NEWTON
 Penemuan Newton tentang gravitasi diilhami dari pengamatan
peristiwa buah apel yang jatuh dari pohonnya ketika dia sedang duduk
di bawah pohon tersebut.
 Newton berusaha menentukan besar gaya gravitasi yang diberikan
bumi pada bulan dengan membandingkan gaya gravitasi pada benda-
benda dipermukaan bumi.

10. ar =
v2
r
=
(2r)2
T2 r
= 0,00272 m/s2
Perbandingan gravitasi bumi dan percepatan
sentripetal bulan didapat :
ar  1/3600 g
hubungan antara percepatan gravitasi dan jarak benda
terhadap bumi yaitu
g  1/R2
Percepatan gravitasi adalah 9,8 m/s2
Percepatan bulan ar = v2/r
Orbit bulan 384.000 km dan periodenya mengorbit bumi selama 27 hari (T = 27)

11. Hukum Gravitasi Newton
Menurut hukum Newton ketiga, ketika bumi memberikan gaya
gravitasi ke benda apapun, seperti bulan misalnya, benda
tersebut akan memberikan gaya yang sama besar tetapi
berlawanana arah pada bumi. Berdasarkan simetri ini, Newton
menyimpulkan bahwa besar gaya gravitasi harus sebanding
dengan kedua massa sehingga :
Setiap partikel di alam menarik partikel lain dengan gaya yang besarnya
berbanding langsung dengan hasil kali masa kedua partikel tersebut dan
berbanding terbalik dengan kwadrat jarak antara kedua massa tersebut.
2
21
r
mm
F  2
21
r
mm
GF 
konstanta gravitasi
2
21
r
mm
F 

12. Tafsiran Newton Terhadap Hukum Kepler
• Hukum Newton tentang gerak dan gravitasi dapat
dipergunakan pada sistem dua benda atau lebih
• Untuk sistem lebih dari dua benda, gaya gravitasinya:
𝐹 = 𝐺
𝑚1 𝑚2
(𝑟1+𝑟2)2
Untuk benda pertama Untuk benda kedua
𝐹 =
𝑚1. 𝑣1
2
𝑟1
2
𝐹 =
𝑚2. 𝑣2
2
𝑟2
2

13. • Sistem dua benda pada koordinat (x1, y1, z1) dan (x2, y2,
z2). Maka pada benda 1 akan bekerja gaya :
m
M
𝑚1
𝑑2
𝑦1
𝑑𝑡2
= −𝐺𝑚1 𝑚2
𝑦1 − 𝑦2
𝑟3
𝑚1
𝑑2
𝑥1
𝑑𝑡2 = −𝐺𝑚1 𝑚2
𝑥1 − 𝑥2
𝑟3
𝑚1
𝑑2
𝑧1
𝑑𝑡2
= −𝐺𝑚1 𝑚2
𝑧1 − 𝑧2
𝑟3
𝑚1
𝑑2 𝑥2
𝑑𝑡2
= −𝐺𝑚1 𝑚2
𝑥2 − 𝑥1
𝑟3
2
2 3
d x x
GM
dt r
 
2
2 3
d y y
GM
dt r
 
2
2 3
d z z
GM
dt r
 
𝑚1
𝑑2 𝑦2
𝑑𝑡2
= −𝐺𝑚1 𝑚2
𝑦2 − 𝑦1
𝑟3
𝑚1
𝑑2 𝑧2
𝑑𝑡2
= −𝐺𝑚1 𝑚2
𝑧2 − 𝑧1
𝑟3

14. Kalikan persamaan dengan y,
dengan x, lalu keduanya dikurangkan sehingga
didapat :
Jika ketiga persamaan di atas kita kita kalikan dengan z,x, dan y,
kemudian ketiganya dijumlahkan, maka diperoleh
a1z + a2x + a3y = 0
persamaan bidang datar, jadi orbit benda terletak pada
sebuah bidang datar yang tetap.
Untuk kecepatan
2
2 3
d x x
GM
dt r
 
2
2 3
d y y
GM
dt r
 
0
d dy dx
x y
dt dt dt
 
  
 
1
dy dy
x y a
dt dt
 
2
dz dy
y z a
dt dt
 
3
dx dz
z x a
dt dt
 

15. • Jarak antara kedua benda dan kecepatan benda dapat
dinyatakan :
r2 = x2 + y2 + z2
Maka
Dimana maka
2
2
GM
v h
r
 

16. Untuk menyederhanakan persoalan
kita tinjau gerak benda dalam
bidang (x, y)
dan
Dari ini Newton menunjukkan bila
sebuah benda yang bergerak
mengelilingi pusat gaya ke mana
benda itu ditarik oleh sebuah gaya
yang berubah dengan 1 / r2,
lintasan benda itu adalah elips,
parabola dan hiperbola.
Hukum kedua kepler, diperoleh dari
kenyataan bahwa gaya yang
diberikan oleh matahari pada planet
diarahkan ke matahari. Hukum
gravitasi Newton menunjuk hukum
ketiga kepler untuk kasus khusus
orbit lingkaran.
Karena bergerak dalam orbit
lingkaran maka planet memiliki
percepatan sentripetal 𝑣2
𝑟 . Maka
gaya gravitasi haruslah sama
dengan gaya sentripetal yang
diperlukan untuk mempertahankan
geraknya.

17. Dari persamaan di atas tampak bahwa massa planet m tidak
terlibat. Besaran
4𝜋2
𝐺𝑀
adalah konstanta, harga
𝑇2
𝑟3 merupakan
perbandingan yang tetap untuk semua planet.

18. Pertanyaan
1. Ikhsannudin (4201414060)
Menurut Kepler lintasan orbit planet ialah elips, bagaimana Kepler membuktikan bentuk
tersebut? Mengapa tidak lingkaran seperti pemikiran orang Yunani Kuno?
Jawab :
• Bentuk elips yang di kemukakan oleh Kepler didasarkan atas perhitungan dan eksentrisitas
(e). Kondisi lingkaran dengan e=0 adalah kondisi yang sangat ideal, yang berlaku pada
sistem dua-benda tak terganggu, (hanya meninjau interaksi dua benda saja), dengan massa
yang berada di pusat sistem jauh lebih dominan dibanding massa yang mengitarinya
(dengan kata lain, massa pusat sistem tepat berada di pusat lingkaran).
• Akan tetapi kenyataannya, ada lebih dari dua obyek yang memiliki massa yang berinteraksi
pada sistem, seperti Tata Surya, walaupun massa Matahari adalah 99% massa dari seluruh
sistem Tata Surya, akan tetapi tidak serta merta pengaruh gaya gravitasi massa planet bisa
saling mengabaikan. Oleh karena itu pusat massa sistem tidaklah berada tepat pada pusat
massa Matahari, dan demikian juga planet-planet tidak bergerak dengan e = 0, akan tetapi
dengan eksentrisitas yang sedikit lebih besar dari nol, artinya cenderung mengikuti gerak
elips, sebagaimana yang telah teramati selama ini.

21. Terimakasih