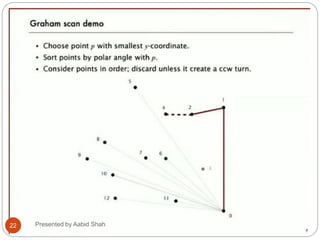
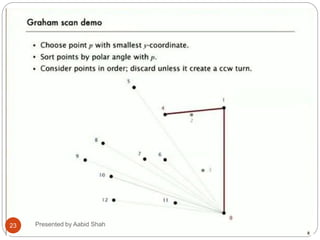
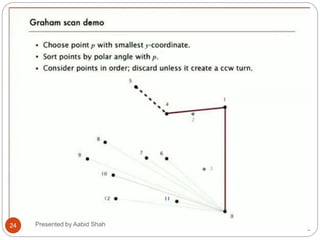
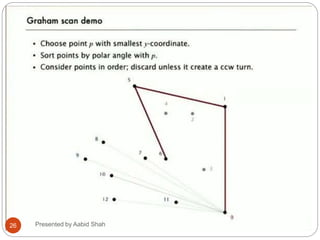
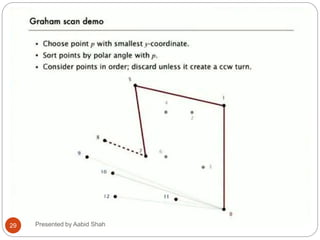
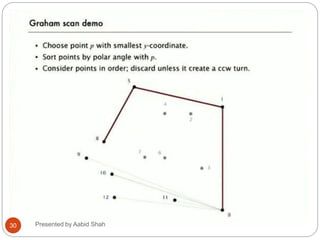
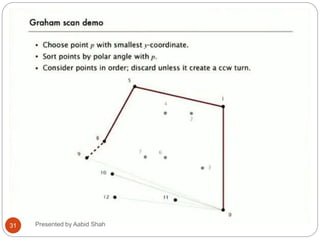
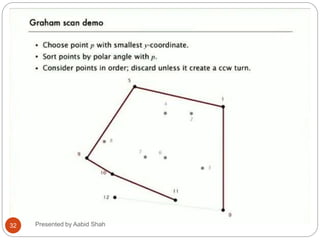
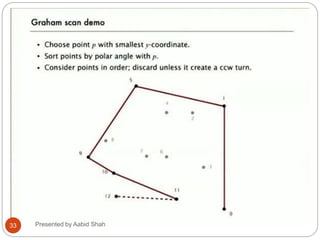
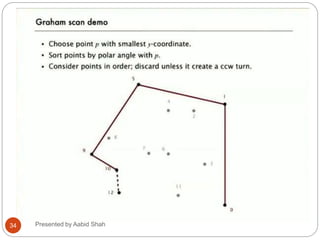
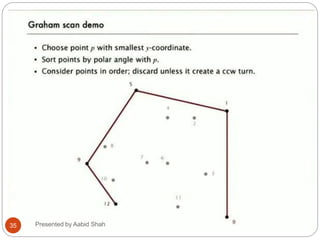
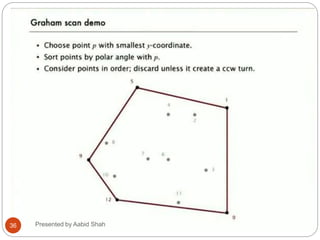
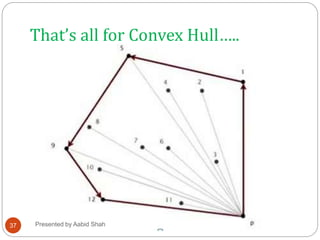
The document presents Aabid Shah's presentation on the divide-and-conquer algorithm and Graham's scan for computing the convex hull of a set of points. It introduces divide-and-conquer as a technique that divides a problem into smaller subproblems, solves the subproblems recursively, and combines the solutions. Graham's scan is described as a divide-and-conquer algorithm that uses a stack to find the convex hull of a set of points in O(n log n) time by sorting points by polar angle and checking for non-left turns. The key steps of Graham's scan and properties of the convex hull are outlined.


![3
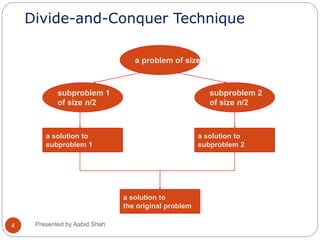
In divide and conquer, method we divide the set
of n points in 0(n) time into two subsets, one
containing the leftmost [n/2] points, and one
containing the right most [n/2] points, recursively
compute the convex hull of the subsets, and then
combine the hulls in 0(n) time. The running time is
described by the familiar recurrence
T(n) =2T(n/2) +o(n),
so the divide and conquer method runs in o(n log
n) time.
Presented by Aabid Shah](https://image.slidesharecdn.com/aabidconvexhull-151102115657-lva1-app6892/85/convex-hull-3-320.jpg)


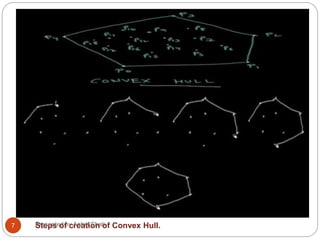
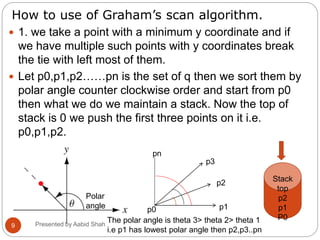
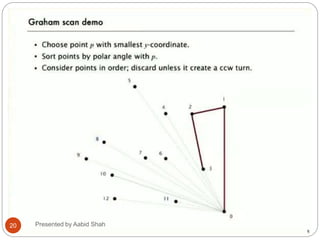
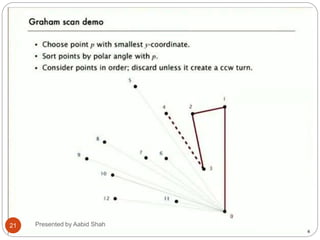
![Graham’s scan Algorithm
1. let p0 be the point in Q with the minimum y-coordinates or the left most
such point in case of a tie
2. let <p1,p2,p3….pn> be the remaining points in Q, sorted by polar angle
in the counter clock wise order around the p0 (if more than one point
has same angle, remove all but that is farthest from p0)
3. let s be the a empty stack i.e. top[s]<--0
4. push (p0,s)
5. Push (p1,s)
6. Push (p2,s)
7. For i = 3 to n
8. While the angle formed by points NEXT-TO-TOP(S),TOP(S),and pi
makes a
non left turn
9. Pop (s)
10. Push (pi,s)
Note: When the algorithm terminates
stack[s] contains exactly the vertices
of Q in the counter clockwise order of
their appearance on the boundary.
8 Presented by Aabid Shah](https://image.slidesharecdn.com/aabidconvexhull-151102115657-lva1-app6892/85/convex-hull-8-320.jpg)