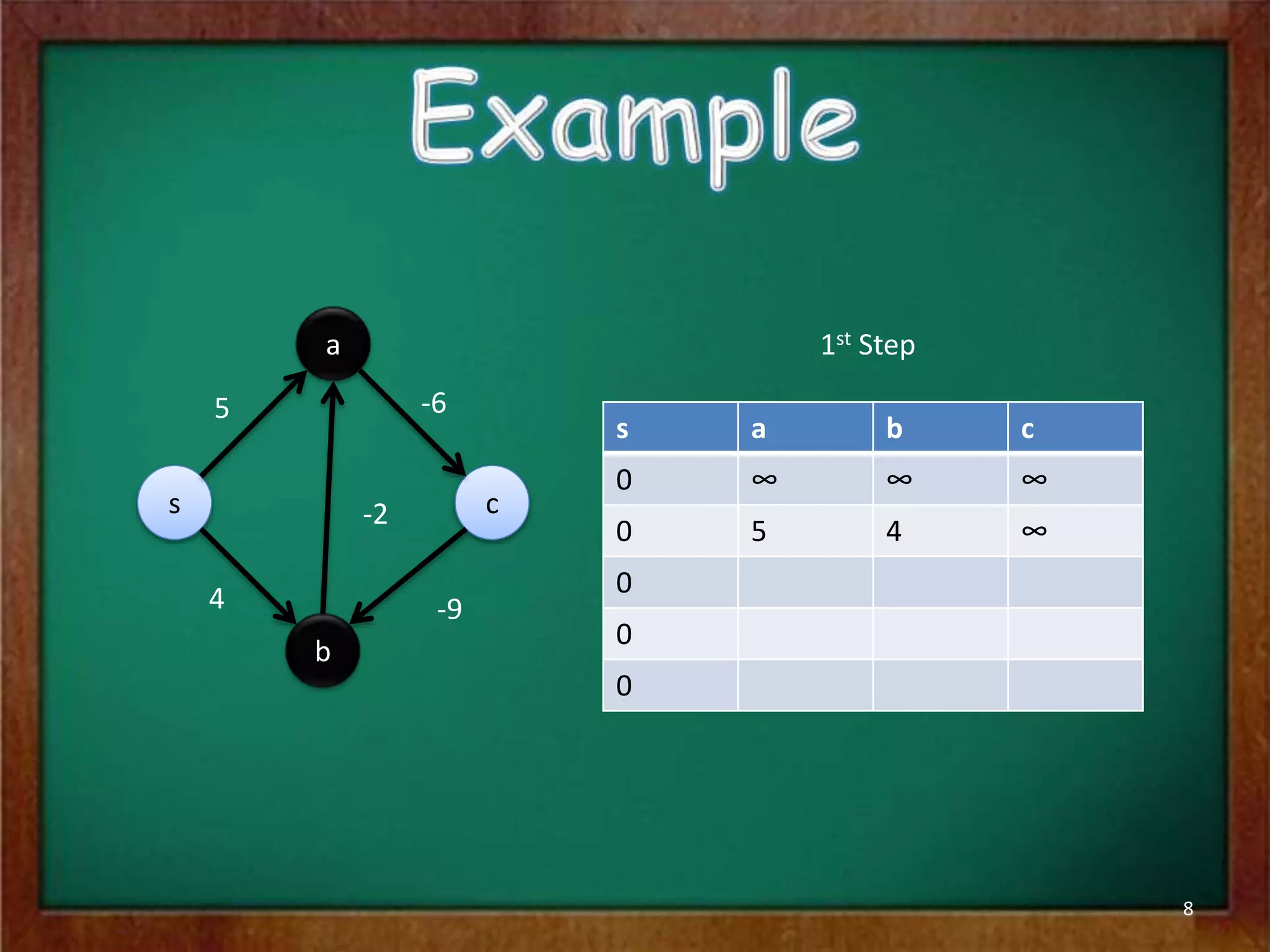
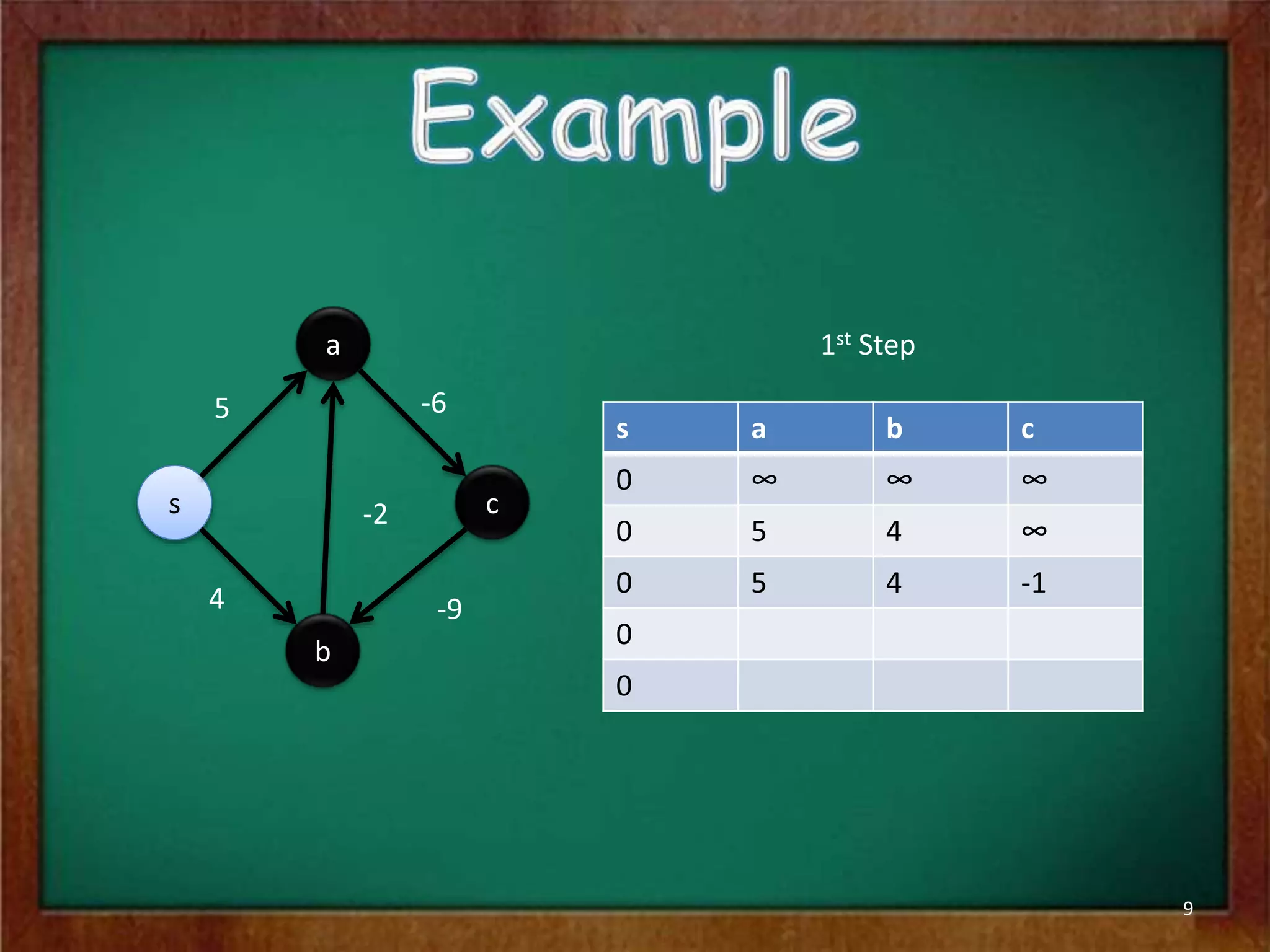
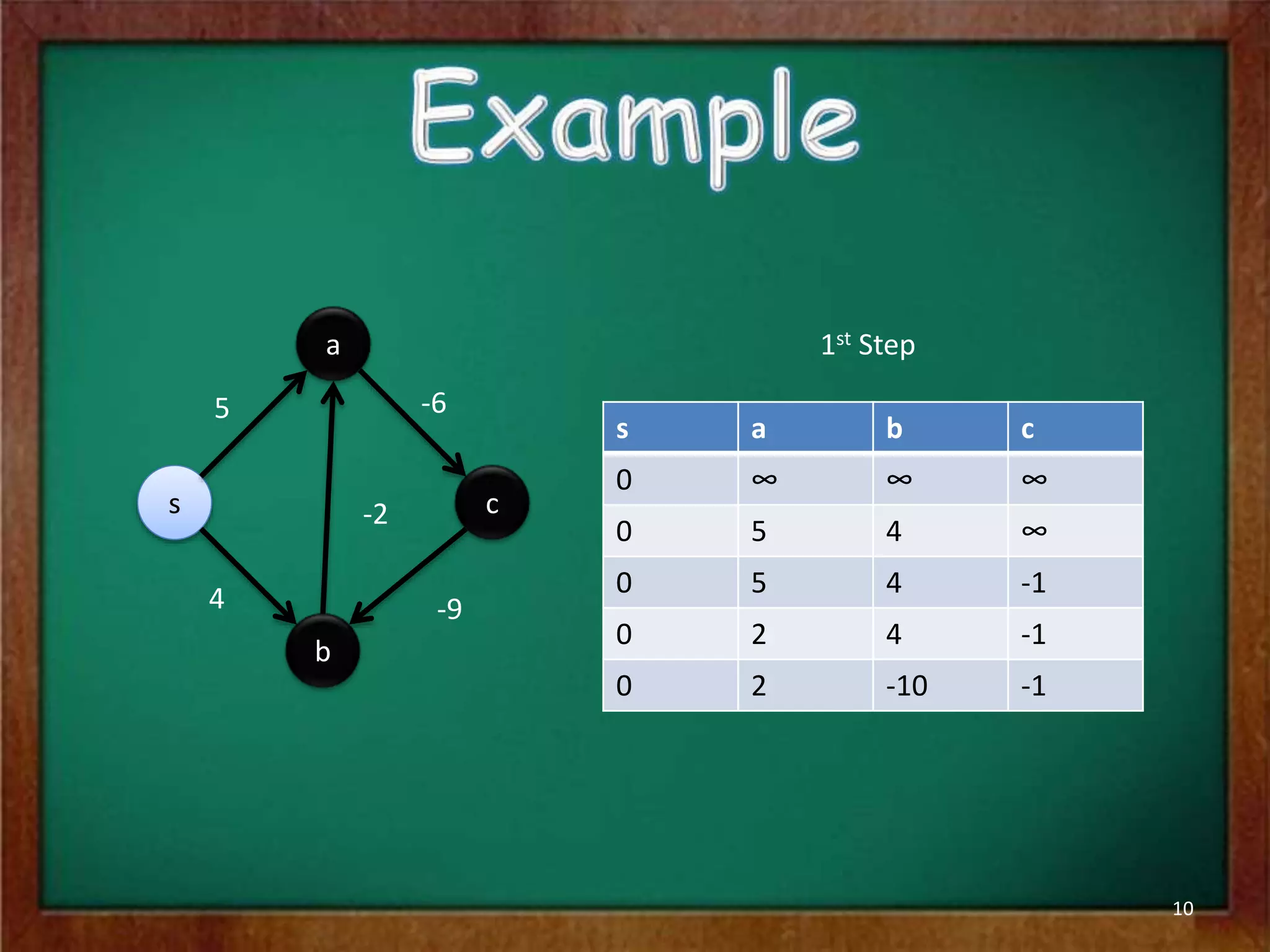
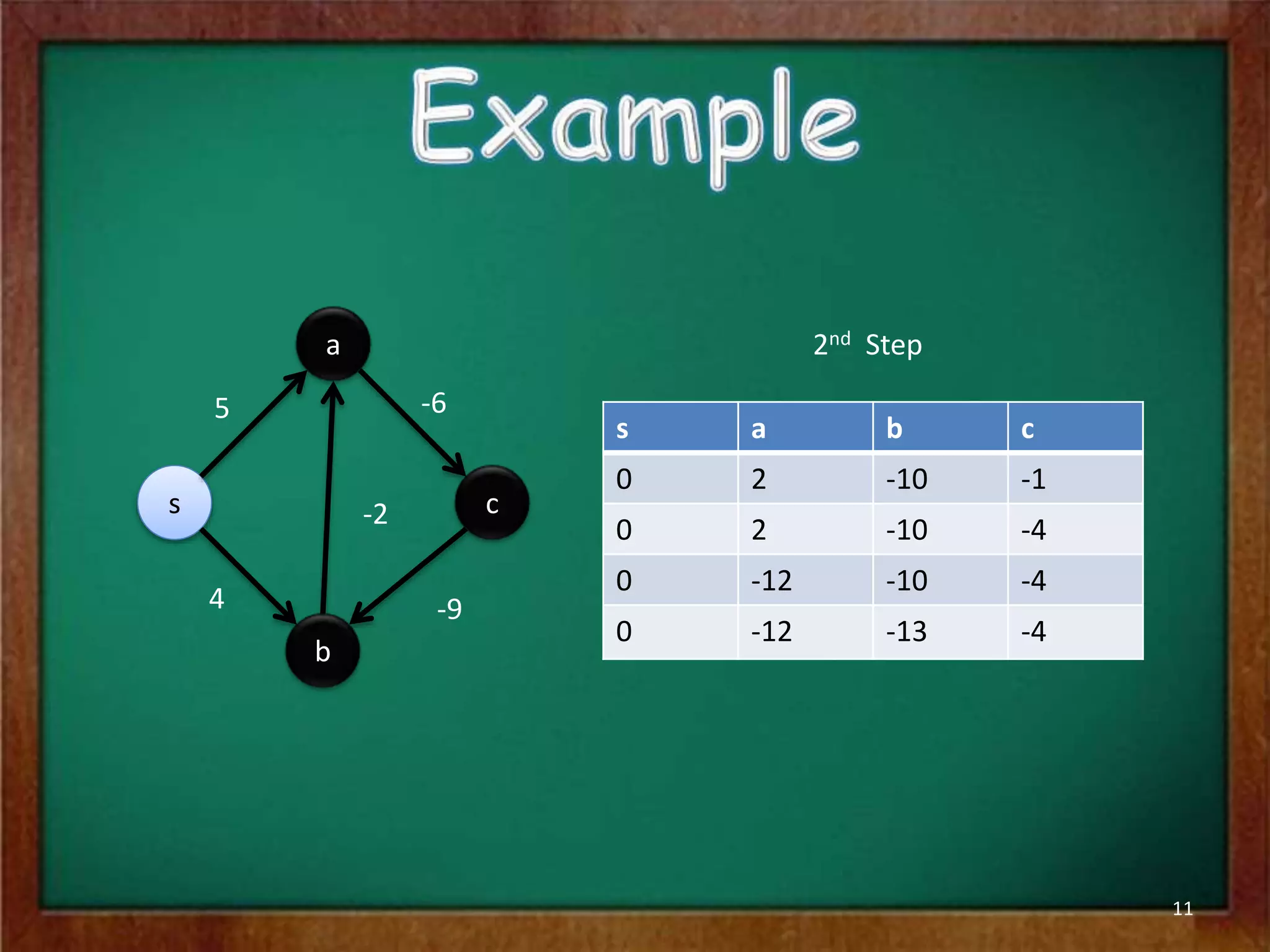
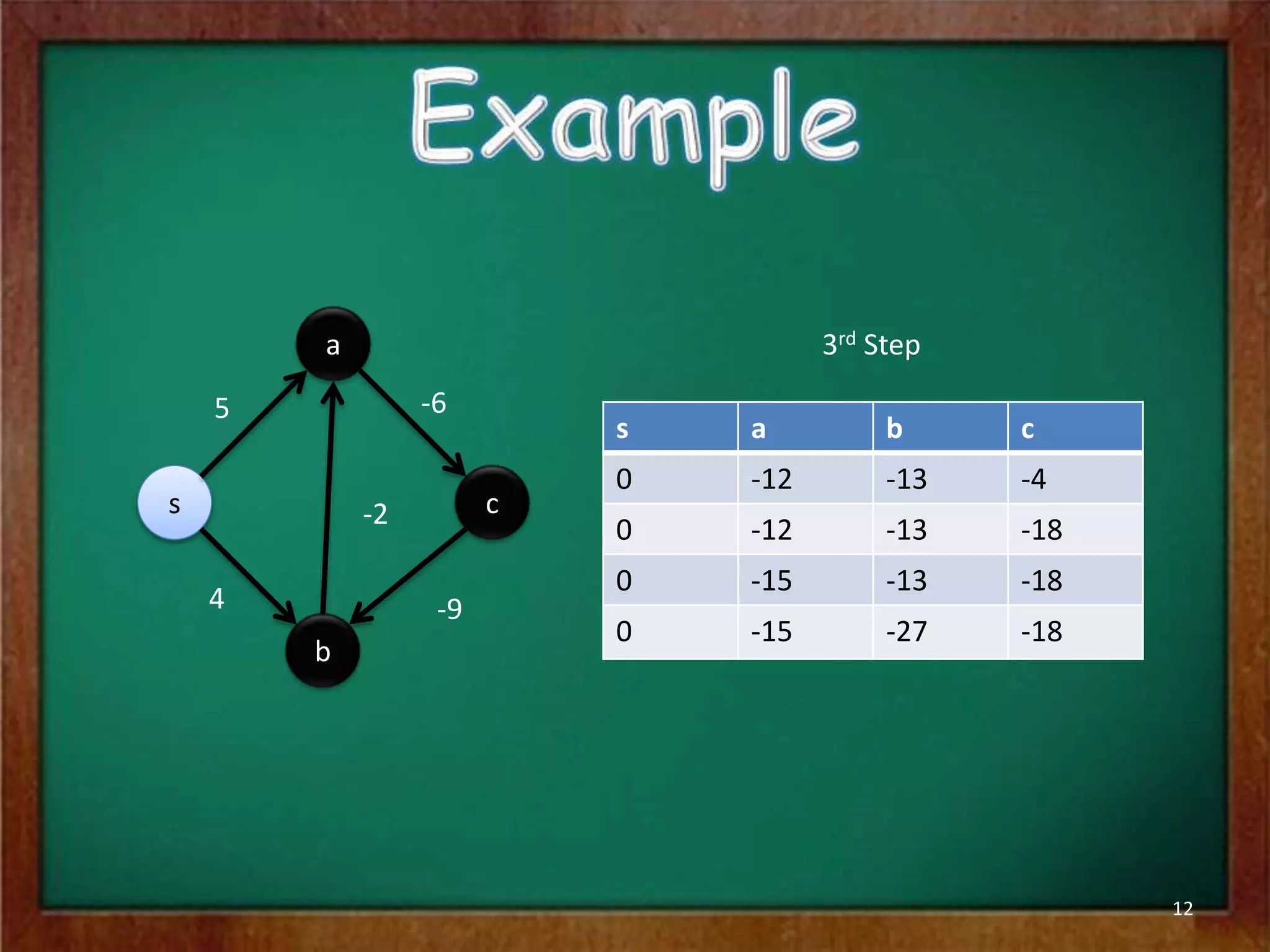
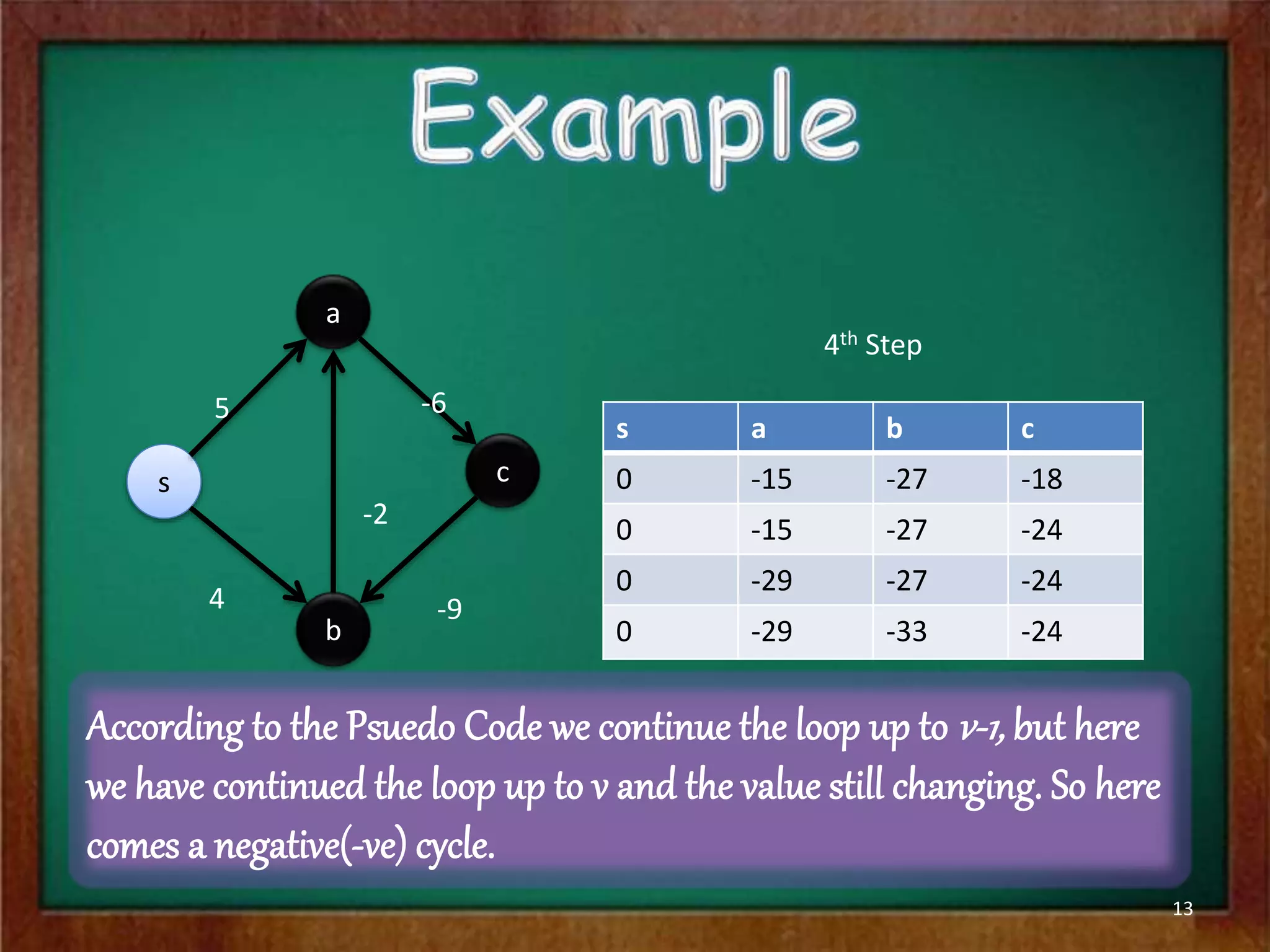
The Bellman-Ford algorithm is used to find the shortest paths from a single source vertex to all other vertices in a graph that may contain negative edge weights. It iterates through all edges |V|-1 times to detect and handle negative cycles, running in O(|V||E|) time. The algorithm initializes distances and predecessors, then repeatedly relaxes edges to update distance values until it converges on the shortest paths or finds a negative cycle.

1. 1

2. 2

3. 3

4. 4

5. oThis is a single source shortest path algorithm.
oThis algorithm can find shortest path from a single
source even if the graph contains negative edges.
oBellman–Ford runs in (|V|.|E|) time, where |V|
and |E| are the number of vertices and edges
respectively.
5

6. 6
INIT(G, s)
for each v  V do
d[v] ← ∞
π[v] ← NIL
d[s] ← 0
RELAX(u, v)
if d[v] > d[u]+w(u,v)
then
d[v] ← d[u]+w(u,v)
π[v] ← u

7. 7
s
a
b
c
5 -6
4
-2
-9
1st Step
s a b c
0 ∞ ∞ ∞
0
0
0
0

8. 8
s
a
b
c
5 -6
4
-2
-9
1st Step
s a b c
0 ∞ ∞ ∞
0 5 4 ∞
0
0
0

9. 9
s
a
b
c
5 -6
4
-2
-9
1st Step
s a b c
0 ∞ ∞ ∞
0 5 4 ∞
0 5 4 -1
0
0

10. 10
s
a
b
c
5 -6
4
-2
-9
1st Step
s a b c
0 ∞ ∞ ∞
0 5 4 ∞
0 5 4 -1
0 2 4 -1
0 2 -10 -1

11. 11
s
a
b
c
5 -6
4
-2
-9
2nd Step
s a b c
0 2 -10 -1
0 2 -10 -4
0 -12 -10 -4
0 -12 -13 -4

12. 12
s
a
b
c
5 -6
4
-2
-9
3rd Step
s a b c
0 -12 -13 -4
0 -12 -13 -18
0 -15 -13 -18
0 -15 -27 -18

13. 13
s
a
b
c
5 -6
4
-2
-9
4th Step
s a b c
0 -15 -27 -18
0 -15 -27 -24
0 -29 -27 -24
0 -29 -33 -24

14. 14

15. 15

16. 16