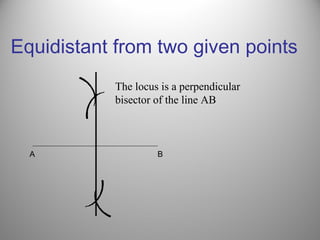
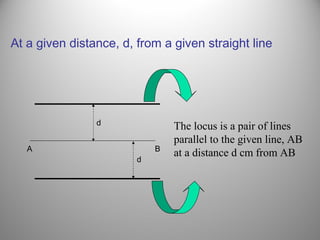
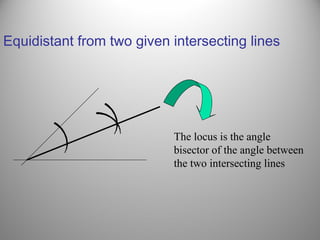
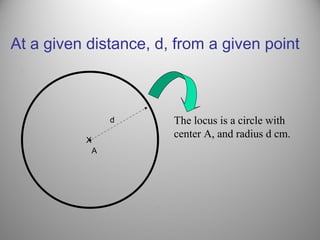
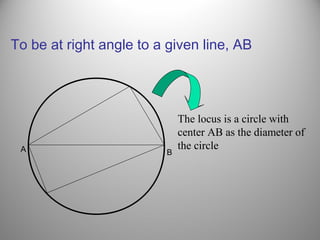
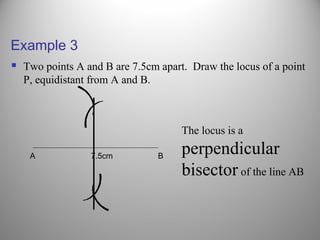
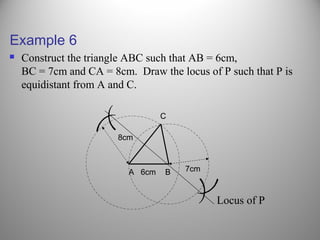
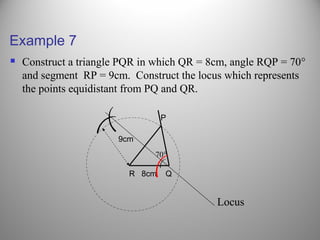
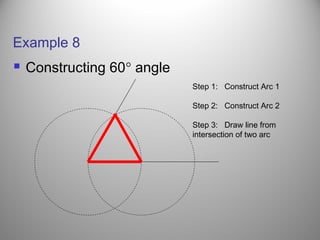
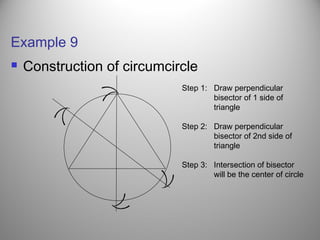
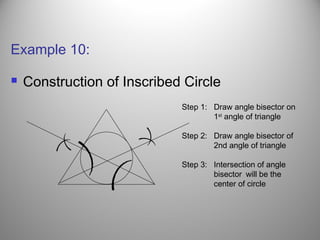
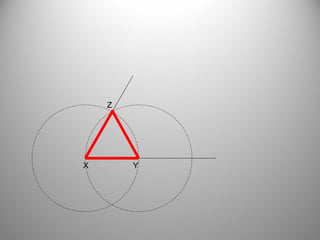
This document defines a locus as a set of points that satisfy certain geometric conditions. It provides examples of loci that are: a given distance from a point or line, equidistant from two points or lines, perpendicular or parallel to a given line, or satisfy other angle or distance criteria. The objectives are to identify loci using a compass, ruler, and protractor. Several examples are worked out step-by-step to illustrate how to construct loci for points satisfying different conditions. Independent practice problems are provided for students to construct their own loci diagrams.

1. UNIT 12.6 LOCUS: AUNIT 12.6 LOCUS: A
SET OF POINTSSET OF POINTS

2. Objectives
 Students are able to identify the locus of a set of
points that are:
 at a given distance d from a given point O
 at a given distance d from a given straight line
 equidistant from two given points
 equidistant from two given intersecting straight lines
 locus of a set of points that satisfy the above conditions
using a compass, ruler and protractor
 a triangle given any three sides/angles using a ruler,
compass and protractor

3. Objectives
 Students are able to identify the locus of a
set of points that are
 >,<, ≥, ≤ a given distance d from a given point O
 >,<, ≥, ≤ a given distance d from a given
straight line
 nearer to point A than point B
 nearer to line A than line B

4. Equidistant from two given points
A B
(
(
(
(
The locus is a perpendicular
bisector of the line AB

5. At a given distance, d, from a given straight line
A B
The locus is a pair of lines
parallel to the given line, AB
at a distance d cm from AB
d
d

6. Equidistant from two given intersecting lines
( ((
The locus is the angle
bisector of the angle between
the two intersecting lines

7. At a given distance, d, from a given point
A
X
d The locus is a circle with
center A, and radius d cm.

8. To be at right angle to a given line, AB
A B
The locus is a circle with
center AB as the diameter of
the circle

9. Example 1
 Describe the locus of a point P, which moves in a plane
so that it is always 4cm from a fixed point O in the
plane.
O
X
4 cm
The locus is a circle with
center O, and radius
4cm.

10. Example 2
 Describe the locus of a point Q, which moves in a
plane, so that it is always 5 cm from a given straight
line, l.
l
The locus is a pair of lines
parallel to the given
line, l, at a distance 5
cm from it.
5 cm
5 cm

11. Example 3
 Two points A and B are 7.5cm apart. Draw the locus of a point
P, equidistant from A and B.
A 7.5cm B
(
(
(
(
The locus is a
perpendicular
bisector of the line AB

12. Example 4
 Draw two intersecting lines l and m. Draw the locus of a point
P which moves such that it is equidistance from l and m.
(
(
( The locus is the angle
bisector of the
angle between the
two intersecting lines
l
m

13. Example 5
 Construct an angle XYZ equal to 60°. Draw the locus of a
point P, which moves such that it is equidistant from XY
and YZ.
(
((
The locus is the angle
bisector of the angle between
the two intersecting linesZ
( 60°
Y
X

14. Example 6
 Construct the triangle ABC such that AB = 6cm,
BC = 7cm and CA = 8cm. Draw the locus of P such that P is
equidistant from A and C.
A 6cm B
C
8cm
7cm
(
(
(
(
Locus of P

15. Example 7
 Construct a triangle PQR in which QR = 8cm, angle RQP = 70°
and segment RP = 9cm. Construct the locus which represents
the points equidistant from PQ and QR.
R 8cm Q
P
9cm
(
(
(
Locus
(
70°

16. Example 8
 Constructing 60° angle
Step 1: Construct Arc 1
Step 2: Construct Arc 2
Step 3: Draw line from
intersection of two arc

17. Example 9
 Construction of circumcircle
((
(
(
(
(
((
Step 1: Draw perpendicular
bisector of 1 side of
triangle
Step 2: Draw perpendicular
bisector of 2nd side of
triangle
Step 3: Intersection of bisector
will be the center of circle

18. Example 10:
 Construction of Inscribed Circle
(
(
(
(
(
(
Step 1: Draw angle bisector on
1st
angle of triangle
Step 2: Draw angle bisector of
2nd angle of triangle
Step 3: Intersection of angle
bisector will be the
center of circle

19. Independent Practice-1
 A long stick leans vertically against a wall. The
stick then slides in such a way that its upper end
describes a vertical straight line down the wall,
while the lower end crosses the floor in a straight
line at right angles to the wall. Construct a
number of positions of the mid point of the stick
and draw the locus.

21. Intersection of Loci
 If two or more loci intersect at a point P, then P satisfies
the conditions of the both loci simultaneously.
 Example:
A B
(
(
(
(
6cm
•The circle is 6cm from point A.
•The perpendicular bisector is at
equidistant from point A and B.
X
YThe point X and Y are both at :
i) 6 cm from A
ii) Equidistant from point A and B

22. Do it Yourself!
Question 1
a) Construct and label triangle XYZ in which XY=10cm,
YZ=7.5cm and angle XYZ = 60°. Measure and write down the
length of XZ.
b) On your diagram, construct the locus of a point
(i) 6cm from point Y
(ii) equidistant from X and Z.
c) The point P, inside the triangle XYZ is 6cm from Y and
equidistant from point X and Y.
(i) Label clearly, on your diagram, point P.
(ii) Measure and write down the length of PX.

23. X Y
Z

24. Do it Yourself!
Question 5
A factory occupies a quadrilateral site ABCD in which
AB=110m, ∠BAD=65°, AD=90m, ∠ADC=110° and
DC=60m.
(a) Using a scale of 1cm to represent 10m, construct a
plan of the quadrilateral ABCD. Measure ∠ABC.

25. Two fuel storage tanks, T1 and T2 are located 30m from C
and 15m from BD respectively.
(b) On the same diagram, draw the locus which represents
all the points inside the quadrilateral which are
i) 30m from C ii) 15m from D
(c) Mark clearly on your diagram, the positions of the
tanks T1 and T2.
(d) By measurement, find the distance between T1 and T2.
Do it Yourself! (Continue)

26. All rights belong to their respective owners.
Copyright Disclaimer Under Section 107 of
the Copyright Act 1976, allowance is made
for "fair use" for purposes such as criticism,
comment, news reporting, TEACHING,
scholarship, and research.
Fair use is a use permitted by copyright
statute that might otherwise be infringing.
Non-profit, EDUCATIONAL or personal use
tips the balance in favor of fair use.