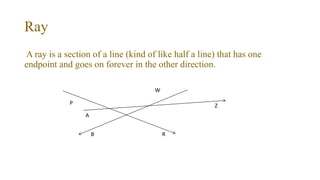
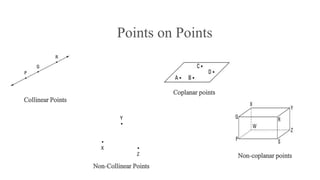
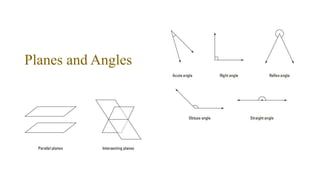
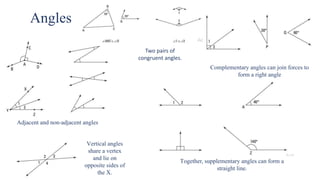
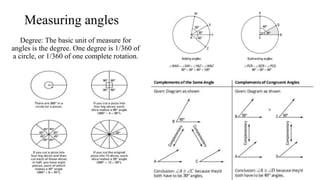
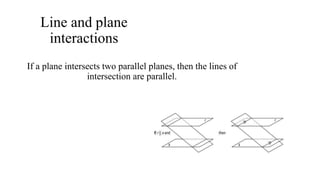
This document provides definitions and explanations of basic geometry concepts including points, lines, line segments, rays, angles, planes, and geometric solids. It defines these concepts and describes their key properties, such as points having no size, lines extending infinitely in both directions, angles formed by two rays with a common endpoint, and planes extending infinitely in two directions. It also covers relationships between these concepts, such as perpendicular and parallel lines, and theorems involving angles, circles, and their intersections with lines and segments.

1. Basic Geometry
By Priyanka

2. Point
A point is like a dot except that it actually has no
size at all; or you can say that it’s infinitely small
(except that even saying infinitely small makes a
point sound larger than it really is). Essentially, a
point is zero-dimensional, with no height, length,
or width, but you draw it as a dot, anyway. You
name a point with a single uppercase letter, as
with points A, D, and T

3. Line
• A line is like a thin, straight wire (although
really it’s infinitely thin — or better yet, it
has no width at all). Lines have length, so
they’re one-dimensional.
• Line goes on forever in both directions,
which is why you use the little double-
headed arrow . Lines are usually named
using any two points on the line, with the
letters in any order. So MQ is the same line
as QM
• Occasionally, lines are named with a
single, italicized, lowercase letter, such as
lines f and g.
M
Q

4. Line segment
A segment is a section of a line that has two endpoints.
M
Q
A
B

5. Ray
A ray is a section of a line (kind of like half a line) that has one
endpoint and goes on forever in the other direction.
P
W
Z
RB
A

6. Angle
• Two rays with the same endpoint
form an angle. Each ray is a side of
the angle, and the common endpoint
is the angle’s vertex. You can name
an angle using its vertex alone or
three points (first, a point on one
ray, then the vertex, and then a point
on the other ray).
• You can call the angle ∠P, ∠RPQ,
or∠QPR.
Q
R
P

7. Plane
A plane is like a perfectly flat sheet of paper
except that it has no thickness whatsoever
and it goes on forever in all directions.It has
infinitely thin and has an infinite length and
an infinite width. Because it has length and
width but no height, it’s two-dimensional.
Planes are named with a single, italicized,
lowercase letter

9. Points on Points
Collinear Points
Non-Collinear Points
Coplanar points
Non-coplanar points

10. Points on Lines
Parallel lines, segments, or rays
Oblique lines,
segments, or
rays
Perpendicular
lines,
segments, or
rays

11. Planes and Angles

12. Angles
Adjacent and non-adjacent angles
Complementary angles can join forces to
form a right angle
Together, supplementary angles can form a
straight line.
Vertical angles
share a vertex
and lie on
opposite sides of
the X.
Two pairs of
congruent angles.

13. Measuring angles
Degree: The basic unit of measure for
angles is the degree. One degree is 1/360 of
a circle, or 1/360 of one complete rotation.

14. Measuring angles in Radians

15. Example of
Geometrical Proofs

17. Triangle’s area

18. Pythagorean Theorem
C
b
a
a2 + b2 = c2
The sum of the squares
on the legs of a right
triangle is equal to the
square on the hypotenuse
(the side opposite the
right angle)

19. Pythagorean
triple
triangles

20. Seven Members
of the Quadrilateral
Family

21. Seven
Members
of the
Quadrilateral
Family

22. Side-Splitter Theorem:
If a line is parallel to a side of a triangle and it intersects the other two
sides, it divides those sides proportionally.

23. Angle-Bisector Theorem:
• If a ray bisects an angle of a triangle, then it divides the opposite side
into segments that are proportional to the other two sides.

24. Circle
» Radius: A circle’s radius — the
distance from its center to a point on
the circle — tells you the circle’s
size. In addition to being a measure
of distance, a radius is also a segment
that goes from a circle’s center to a
point on the circle.
» Chord: A segment that connects
two points on a circle is called a
chord.
» Diameter: A chord that passes
through a circle’s center is a diameter
of the circle. A circle’s diameter is
twice as long as its radius.
» Radii size: All radii of a circle are
congruent.
» Perpendicularity and bisected chords:
• If a radius is perpendicular to a chord, then
it bisects the chord.
• If a radius bisects a chord (that isn’t a
diameter), then it’s perpendicular to
the chord.
» Distance and chord size:
• If two chords of a circle are equidistant
from the center of the circle, then
they’re congruent.
• If two chords of a circle are congruent,
then they’re equidistant from its
center.» Circumference=2πr=π d or
» Area Circle=π r2

25. Arc length
• The length of an arc (part of the
circumference, is equal to the
circumference of the circle (2πr )
times the fraction of the circle
represented by the arc’s measure (note
that the degree measure of an arc is
written like mAB)
• Length AB=(mAB/360)*2πr

26. Tangent-Secant Power Theorem
If a tangent and a secant are drawn
from an external point to a circle,
then the square of the length of the
tangent is equal to the product of
the length of the secant’s external
part and the length of the entire
secant.
The tangent secant power theorem: (tangent)2 = (outside) (whole)

27. Secant-Secant Power Theorem
If two secants are drawn from an
external point to a circle, then the
product of the length of one
secant’s external part and the
length of that entire secant is equal
to the product of the length of the
other secant’s external part and the
length of that entire secant.
The secant-secant power theorem: (outside) (whole) = (outside) (whole).

28. Chord-Chord Power Theorem
If two chords of a circle intersect,
then the product of the lengths of
the two parts of one chord is equal
to the product of the lengths of the
two parts of the other chord.
The chord-chord power theorem: (part) (part) =(part) (part).

29. The four ways to determine a plane

30. Line and plane
interactions

31. If a plane intersects two parallel planes, then the lines of
intersection are parallel.
Line and plane
interactions

32. Geometric Solids

33. Geometric
Solids