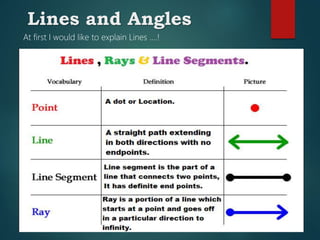
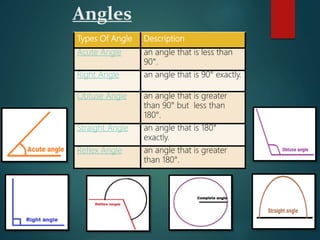
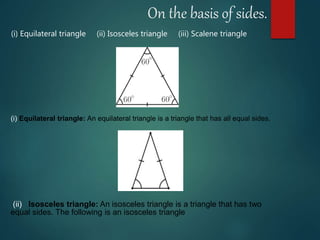
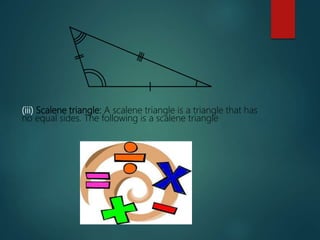
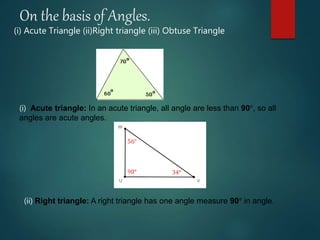
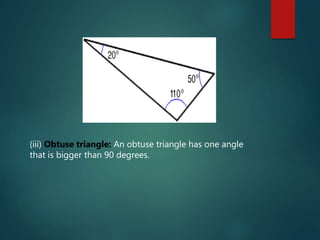
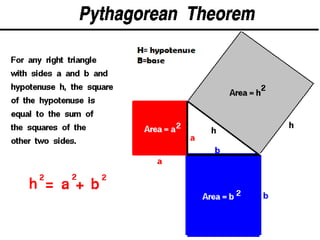
The document outlines concepts related to lines, angles, and triangles, including types of angles (acute, right, obtuse, straight, reflex) and properties of parallel lines intersected by a transversal. It describes different types of triangles based on side lengths (equilateral, isosceles, scalene) and angles (acute, right, obtuse), along with important geometric theorems. The presentation emphasizes fundamental geometry principles and concludes with an acknowledgment of the endless nature of mathematics.

2. The Course Content
Lines & Angles Properties Of
Parallel Lines
Properties Of
Triangles

4. Lines and Angles
At first I would like to explain Lines ….!

5. Some more types of Lines.

6. Angles
Types Of Angle Description
Acute Angle an angle that is less than
90°.
Right Angle an angle that is 90° exactly.
Obtuse Angle an angle that is greater
than 90° but less than
180°.
Straight Angle an angle that is 180°
exactly.
Reflex Angle an angle that is greater
than 180°.

8. Properties of Parallel Lines
At first, we should know,
 What is Parallel line?
:- Lines are said to be parallel when they do not intersected however if
extended.
 What is Transversal?
:- A line which intersect two or more lines at distinct points is called
Transversal.
Let’s Go through the property of
Parallel Lines.

9. Properties
 Corresponding angle
(∠1, ∠5), (∠2, ∠6), (∠3, ∠7) & (∠4, ∠8)
 Alternate Interior angle
(∠3, ∠5) & (∠4, ∠6)
 Alternate Exterior angle
(∠2, ∠8) & (∠1, ∠7)
 Consecutive interior angle
(∠3, ∠6) & (∠4, ∠5)
 Linear Property
Sum of all angles on a line = 180°

10. Theorem :
If two parallel lines are intersected by a transversal, then
(i) The angles of each pair of corresponding angle are equal
, i.e., (∠1, ∠5), (∠2, ∠6), (∠3, ∠7) & (∠4, ∠8).
(ii) The angles of each pair of alternate interior angle are
equal i.e., (∠3= ∠5) and (∠4 = ∠6).
(iii) the sum of two consecutive interior angles is 180°.
i.e., (∠3+ ∠6) = 180° and (∠4 + ∠5) = 180°.

12. Properties of Triangles.
At first, we should know,
 What is a Triangle?
A triangle is a polygon with three edges and three
vertices. It is one of the basic shapes in geometry.
Triangles are divided into two basis:
 On the basis of length of Sides.
 On the basis of the angles of sides.

13. On the basis of sides.
(i) Equilateral triangle: An equilateral triangle is a triangle that has all equal sides.
(i) Equilateral triangle (ii) Isosceles triangle (iii) Scalene triangle
(ii) Isosceles triangle: An isosceles triangle is a triangle that has two
equal sides. The following is an isosceles triangle

14. (iii) Scalene triangle: A scalene triangle is a triangle that has
no equal sides. The following is a scalene triangle

15. On the basis of Angles.
(i) Acute Triangle (ii)Right triangle (iii) Obtuse Triangle
(i) Acute triangle: In an acute triangle, all angle are less than 90°, so all
angles are acute angles.
(ii) Right triangle: A right triangle has one angle measure 90° in angle.

16. (iii) Obtuse triangle: An obtuse triangle has one angle
that is bigger than 90 degrees.

17. Therefore:
 A triangle cannot have more than one right
angle:
 A triangle cannot have more than one
obtuse angle:
 In a right angled Triangle, the sum of two
acute angle is 90°.

19. Now I would like to end my Power point, as there is no end of Mathematics
hence My presentation will also not end.
I’m sure that you would have got the concept of the chapters like Lines &
Angles, Properties of parallel Lines & Properties of Triangles.
Thank You….!

20. Maths Project
By :-
Name :- Chandra Prakash Garg
Class :- VII ‘A’
Roll :- 14
Sub :- Maths
Submitted to :- Mr. Ranjeet Sir