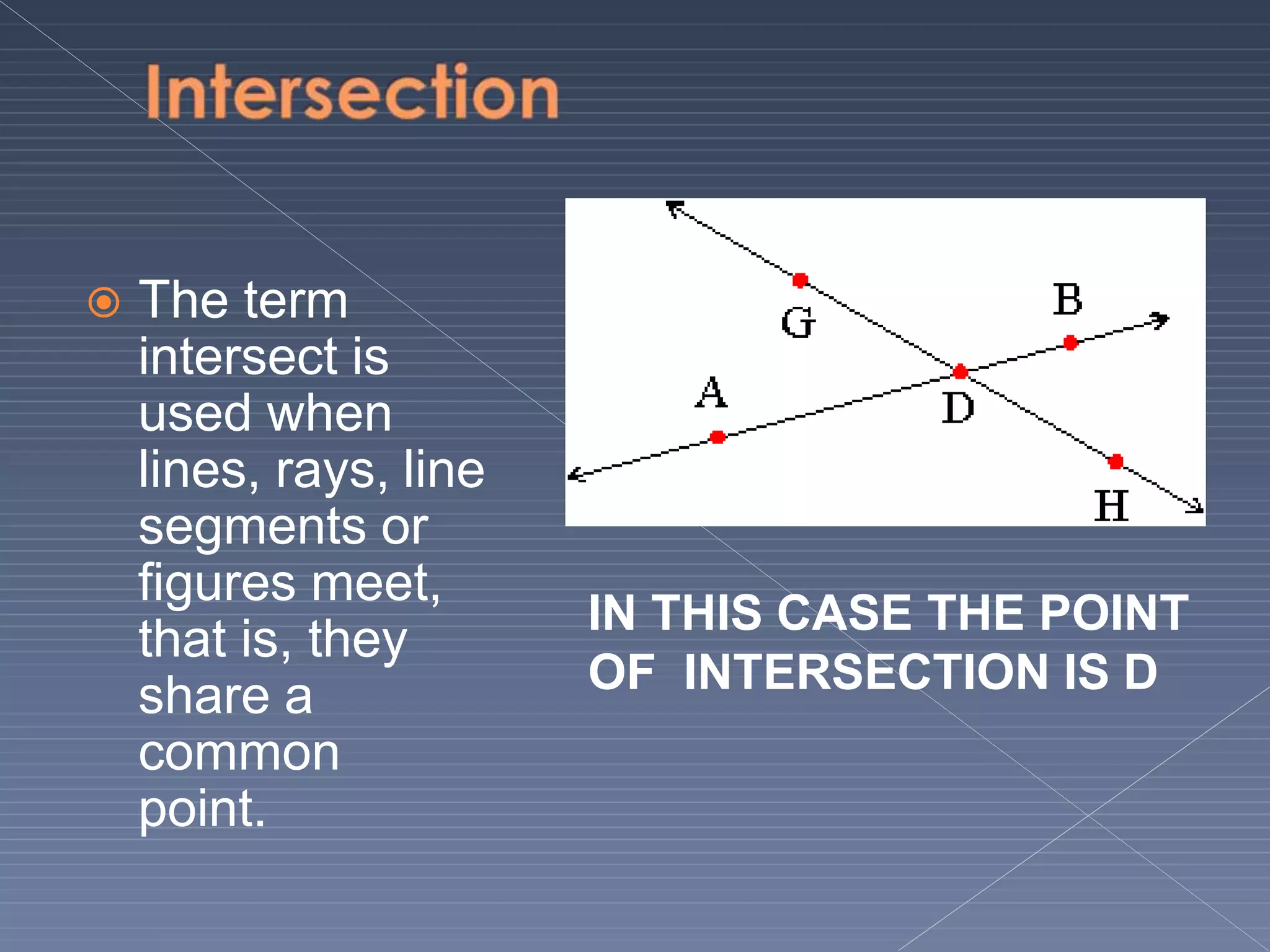
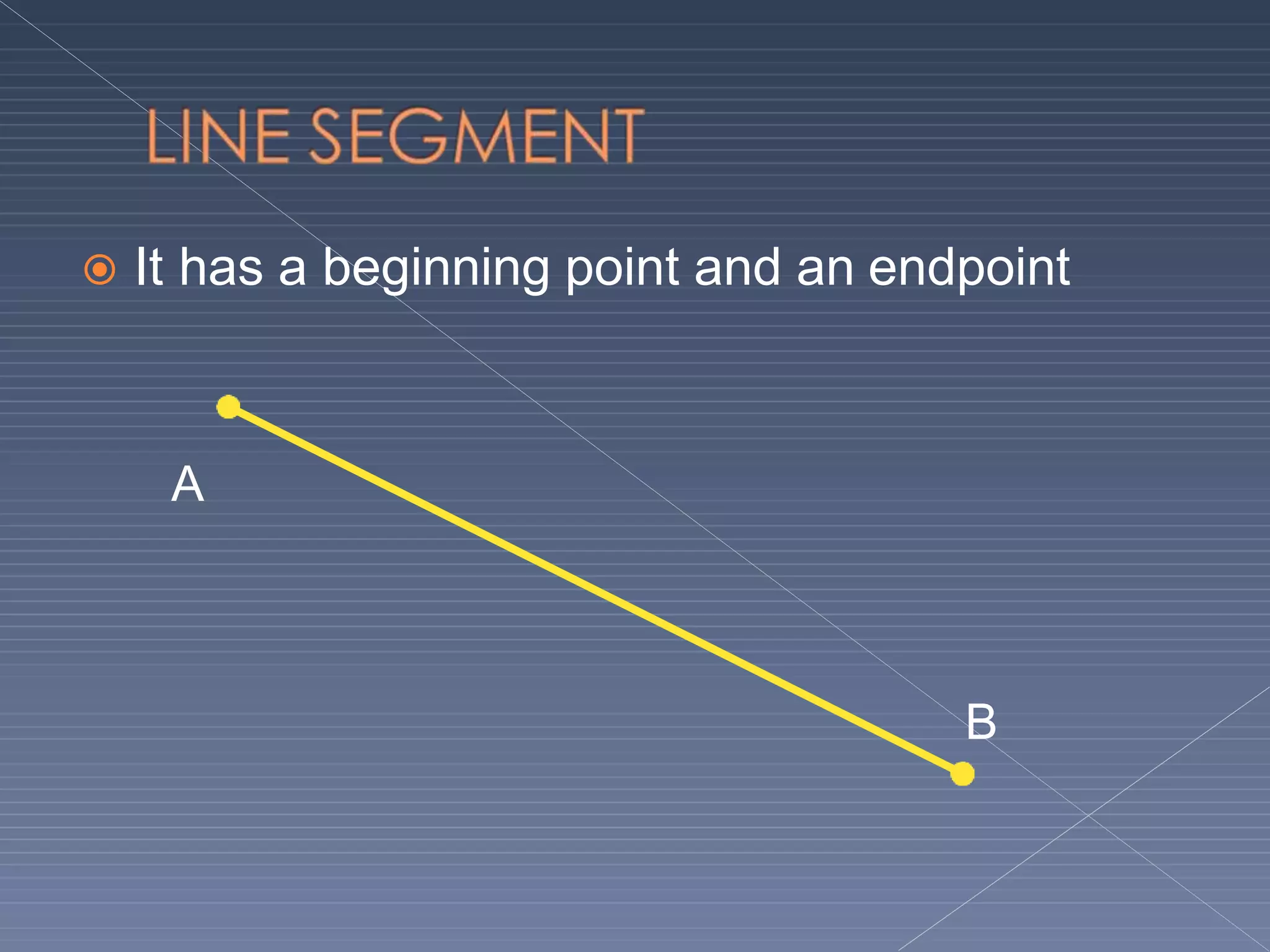
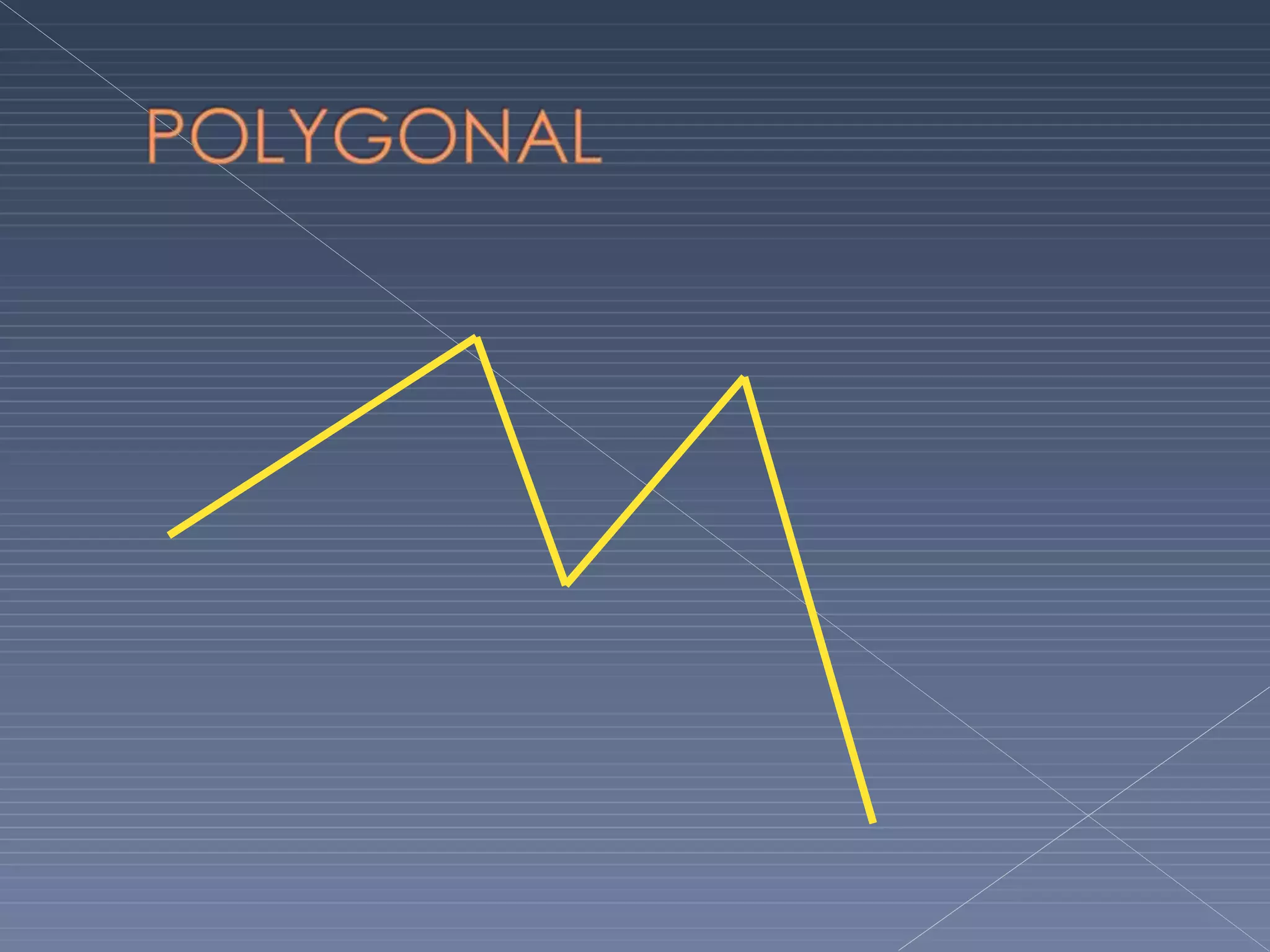
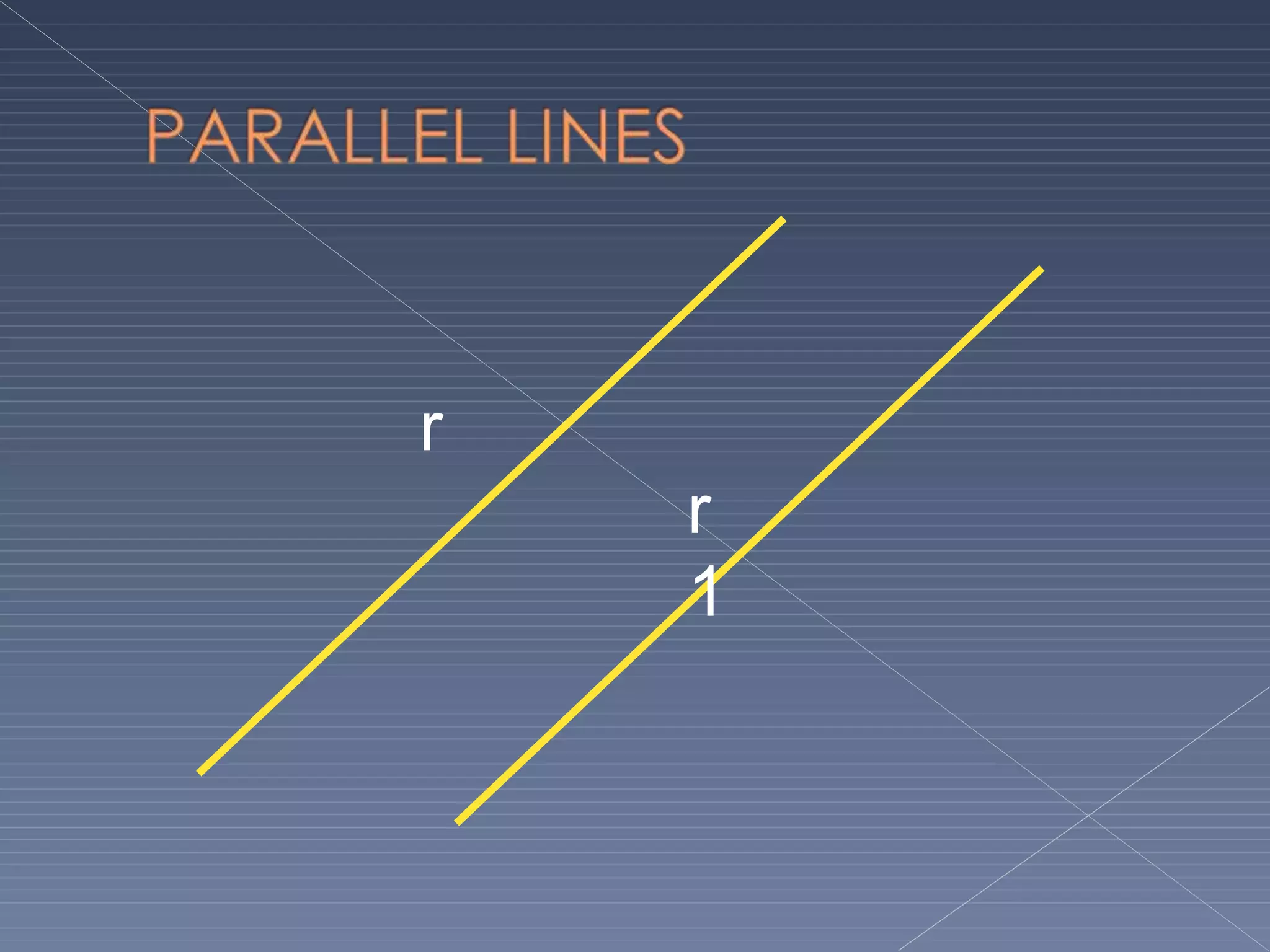
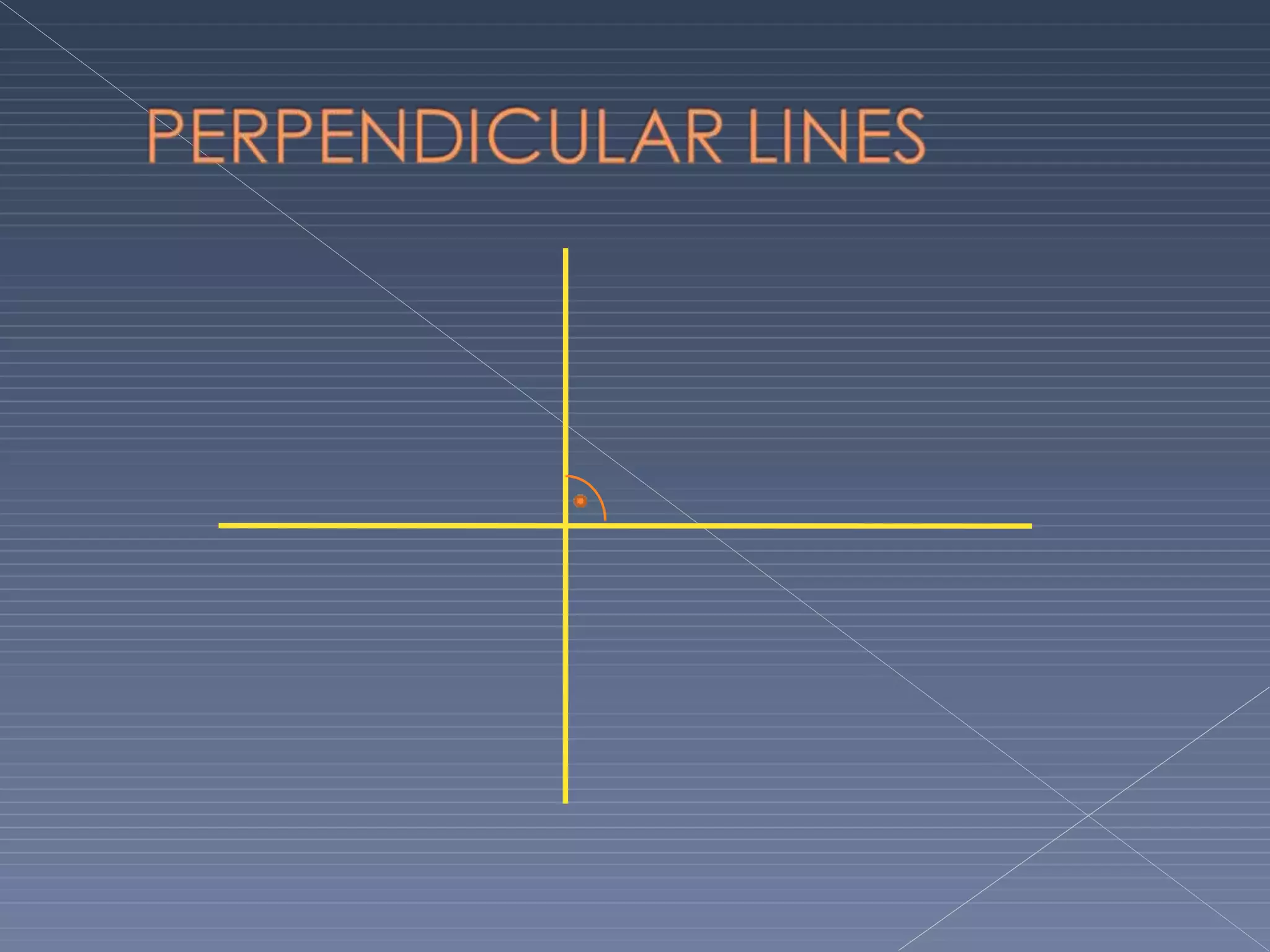
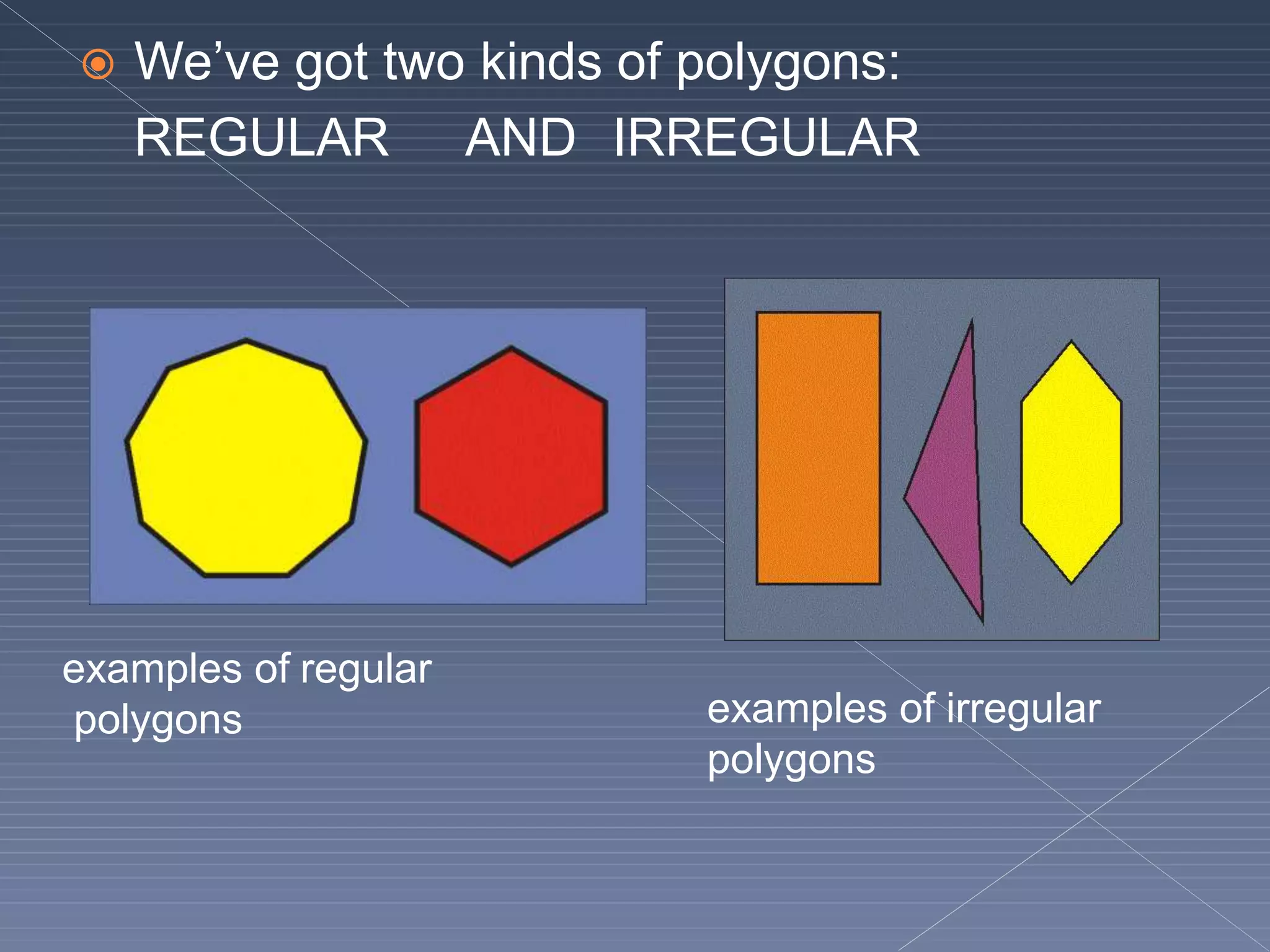
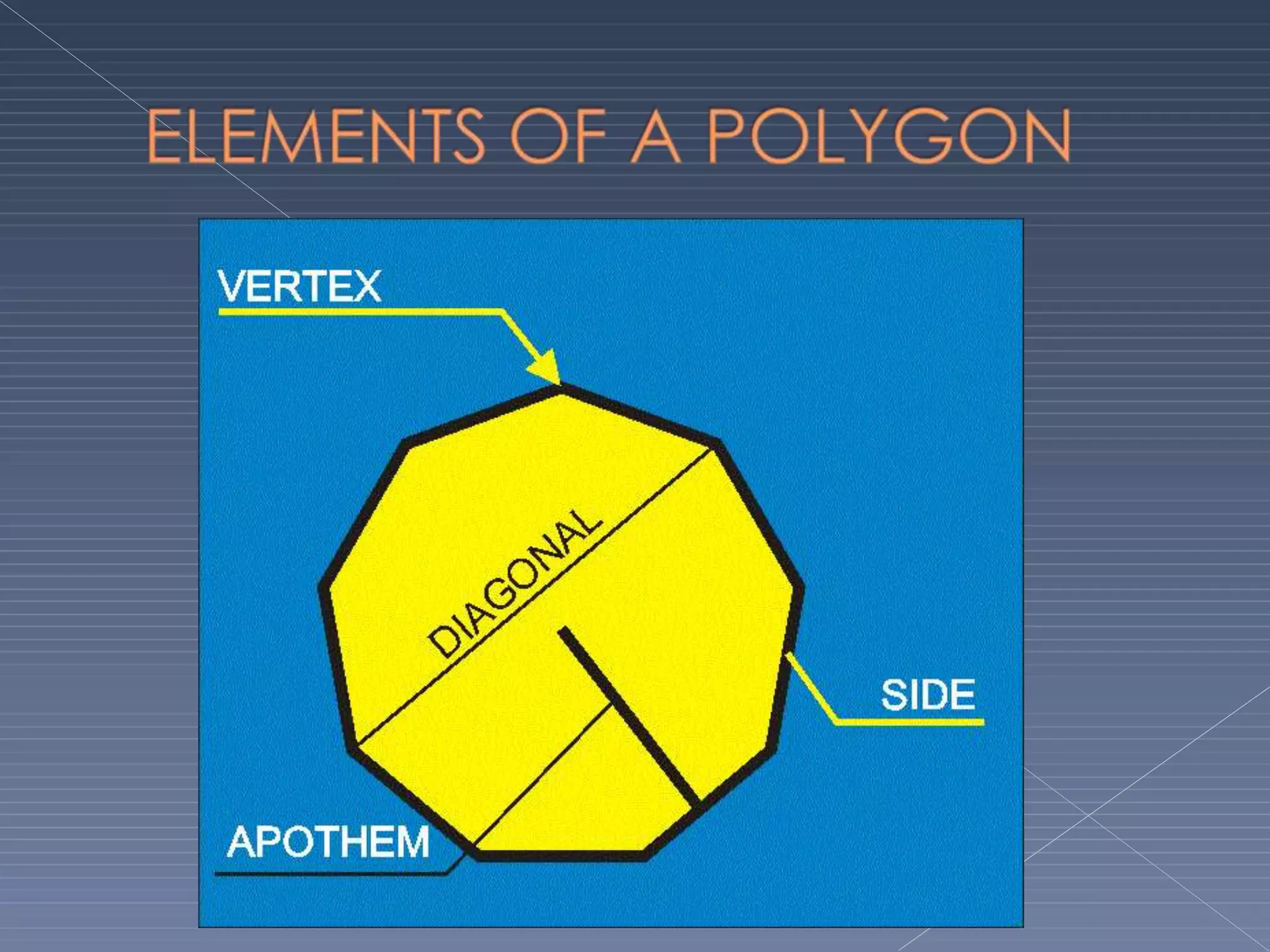
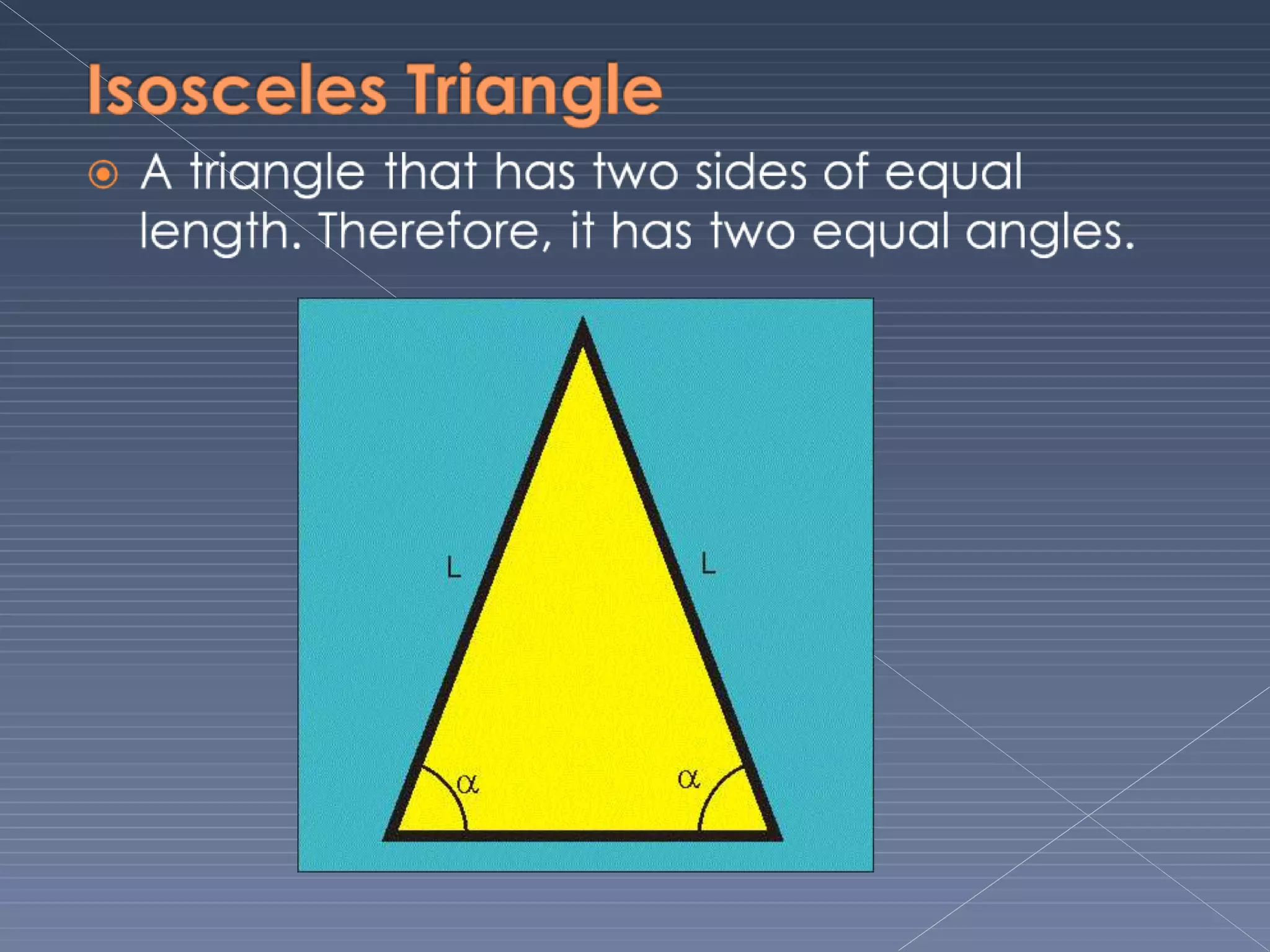
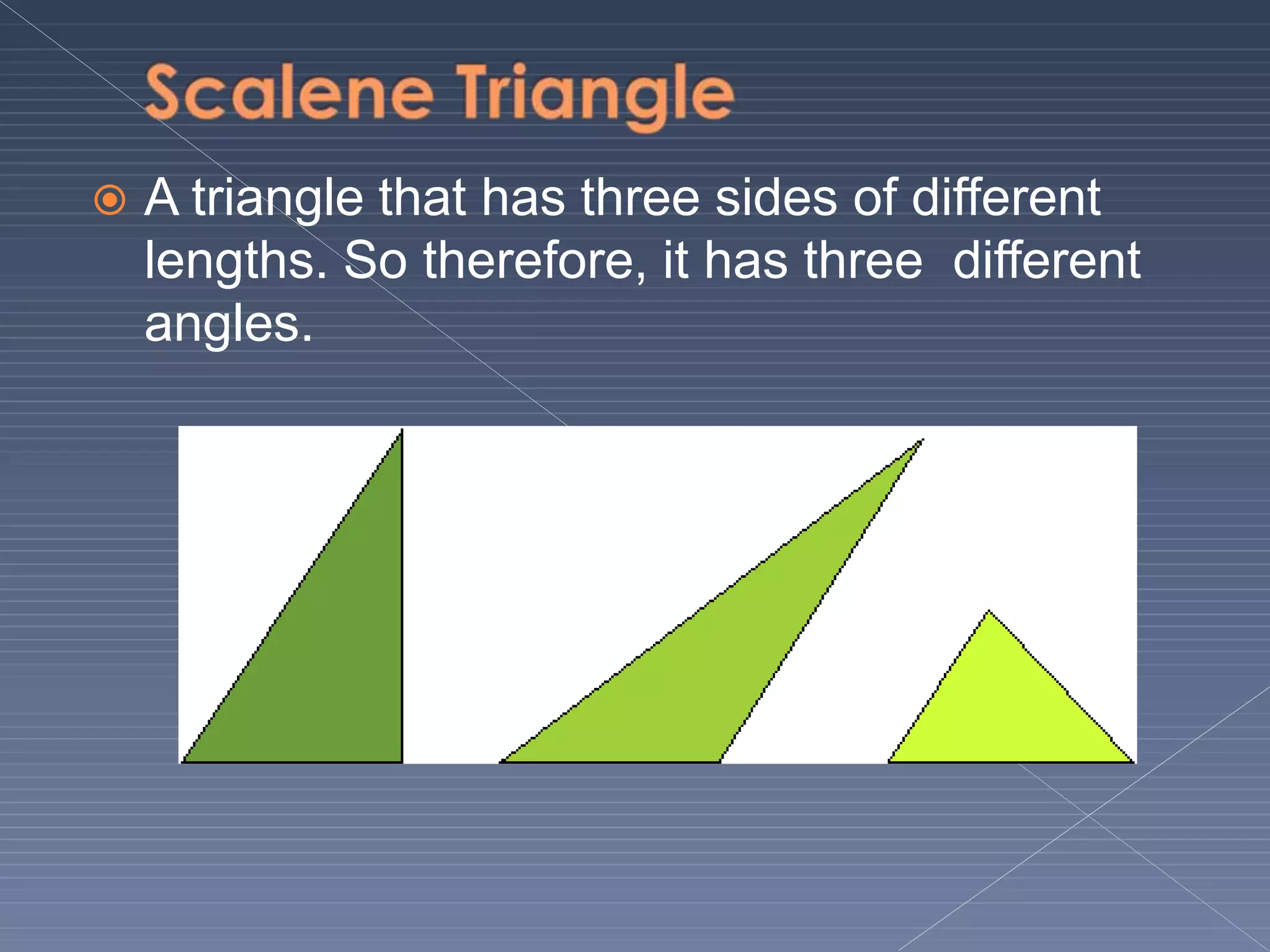
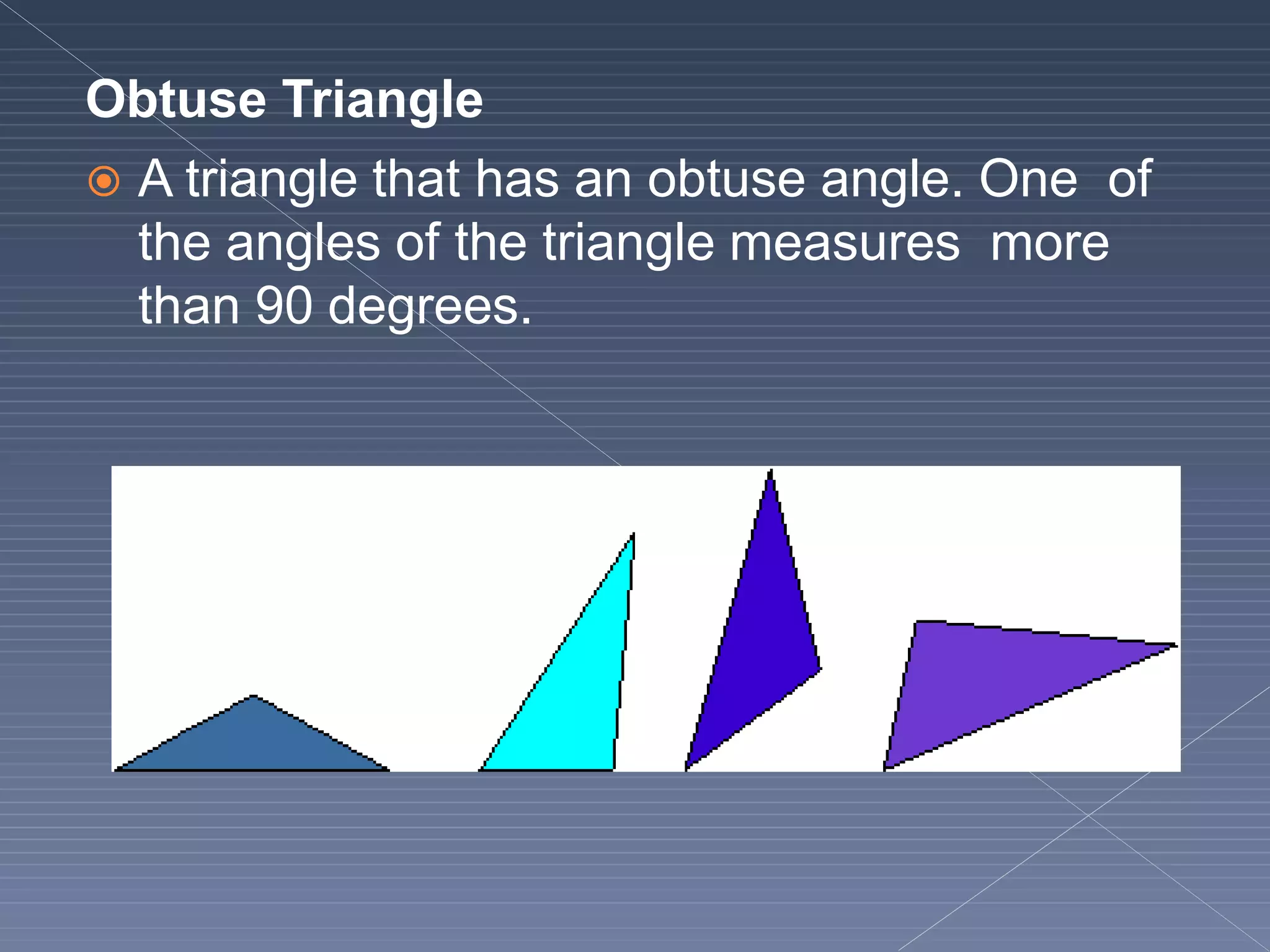
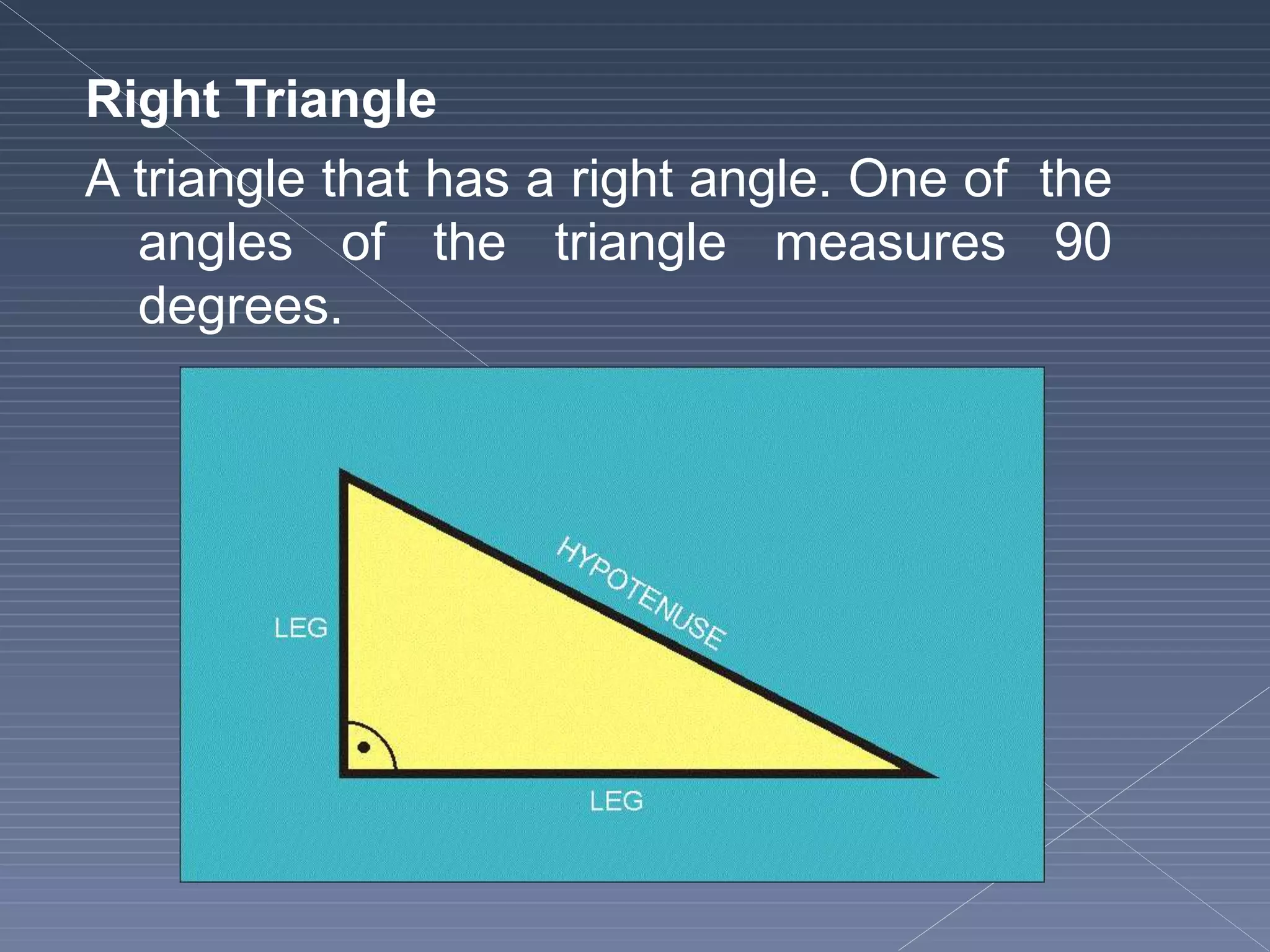
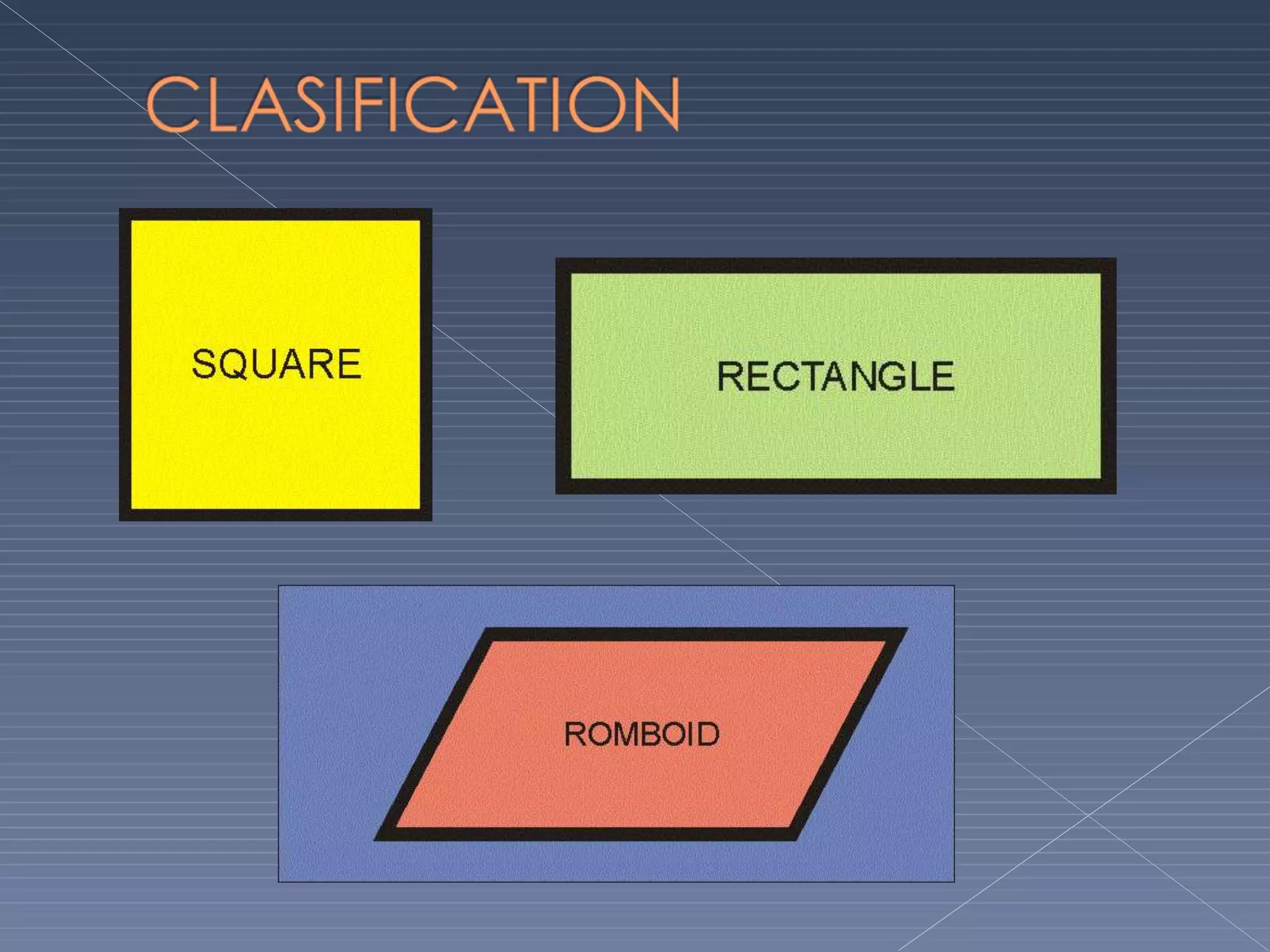
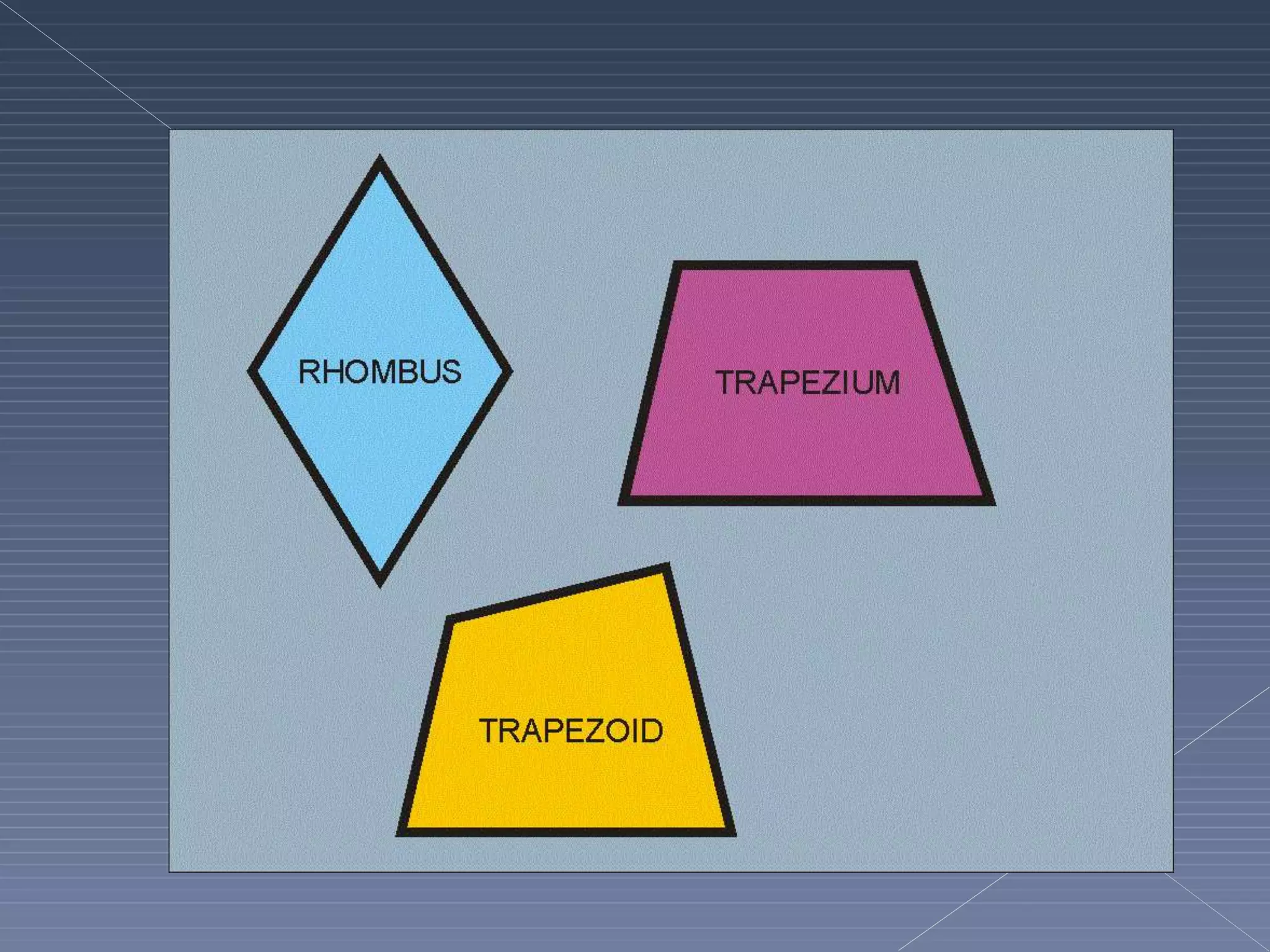
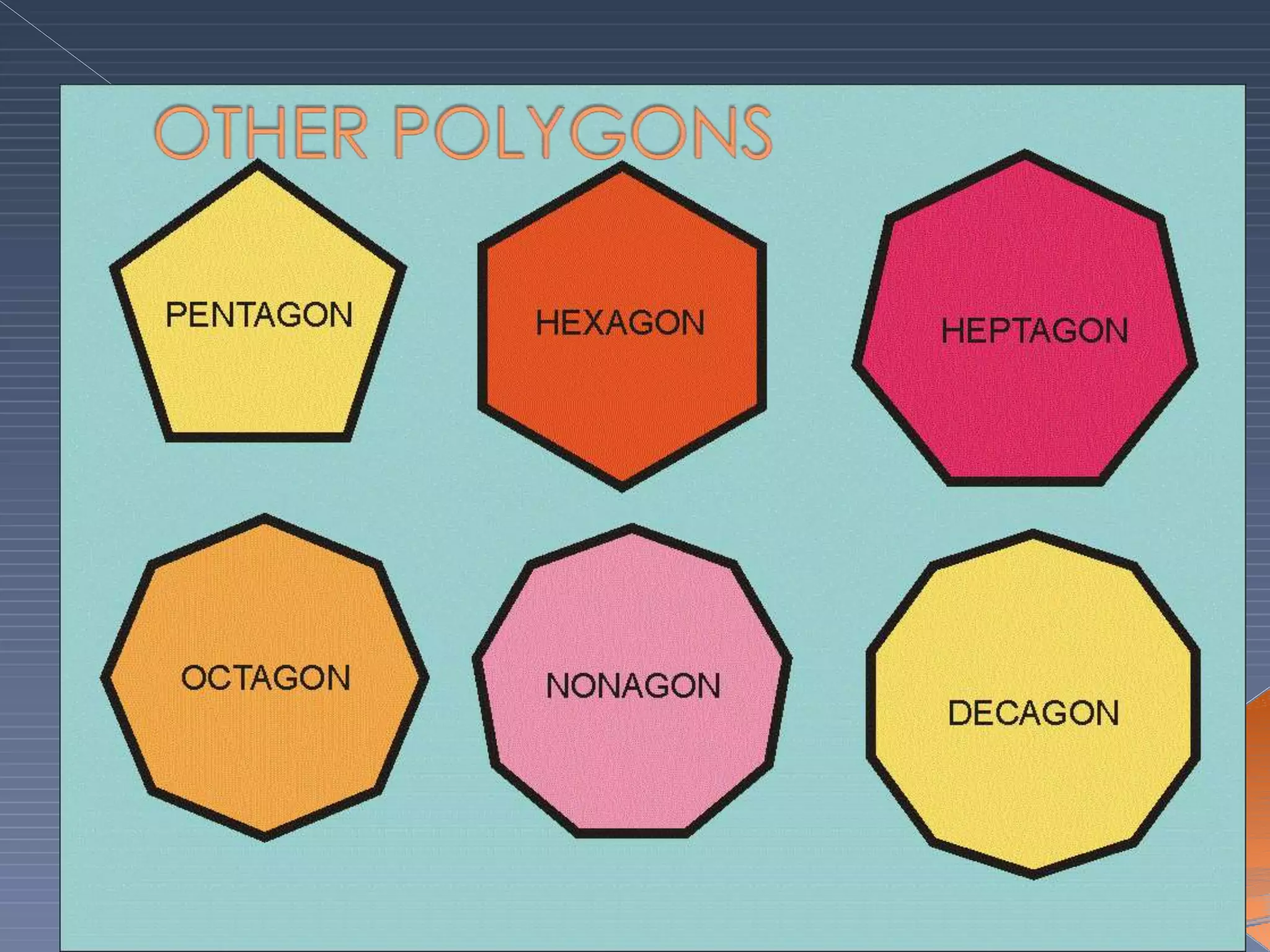
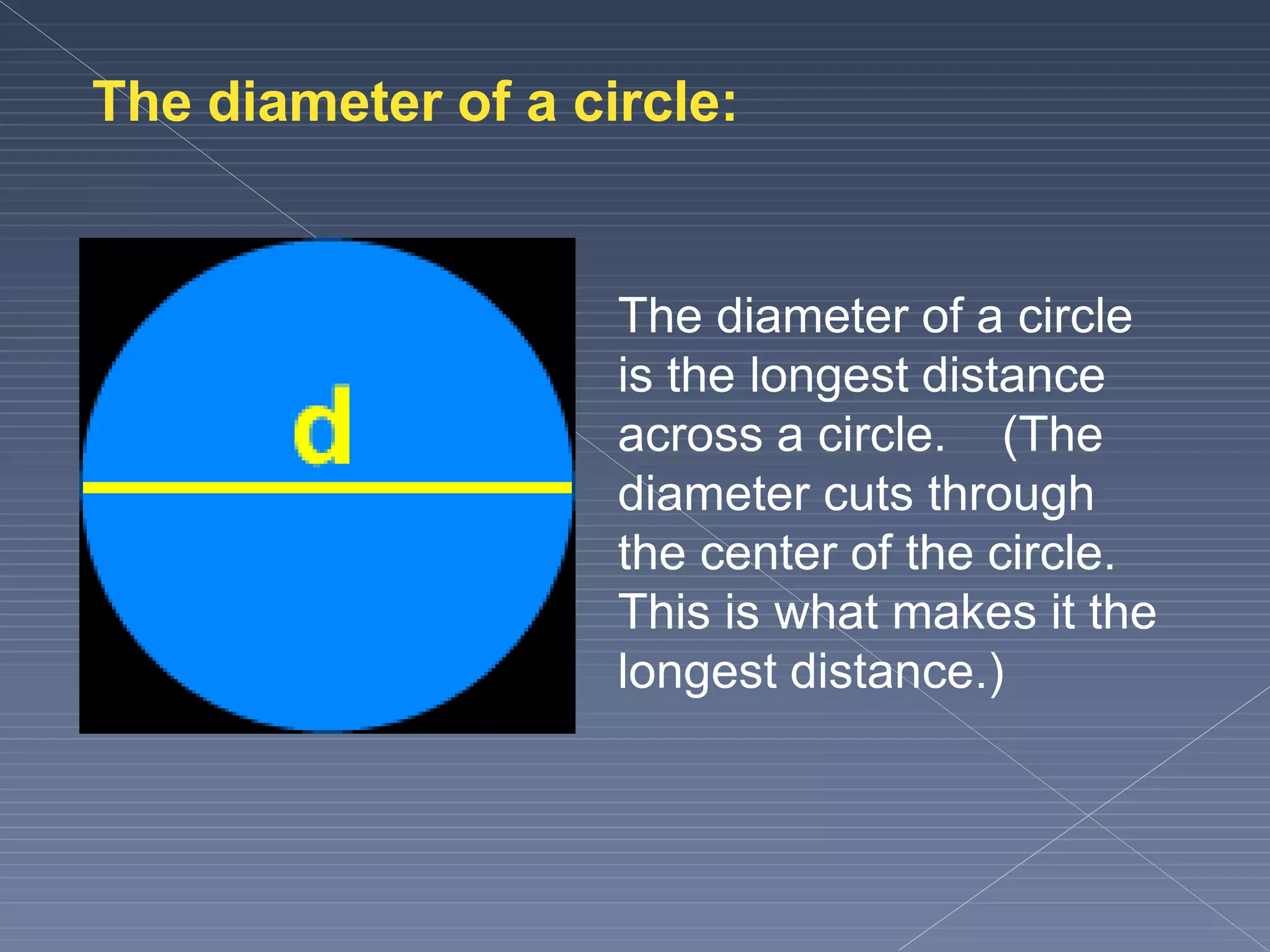
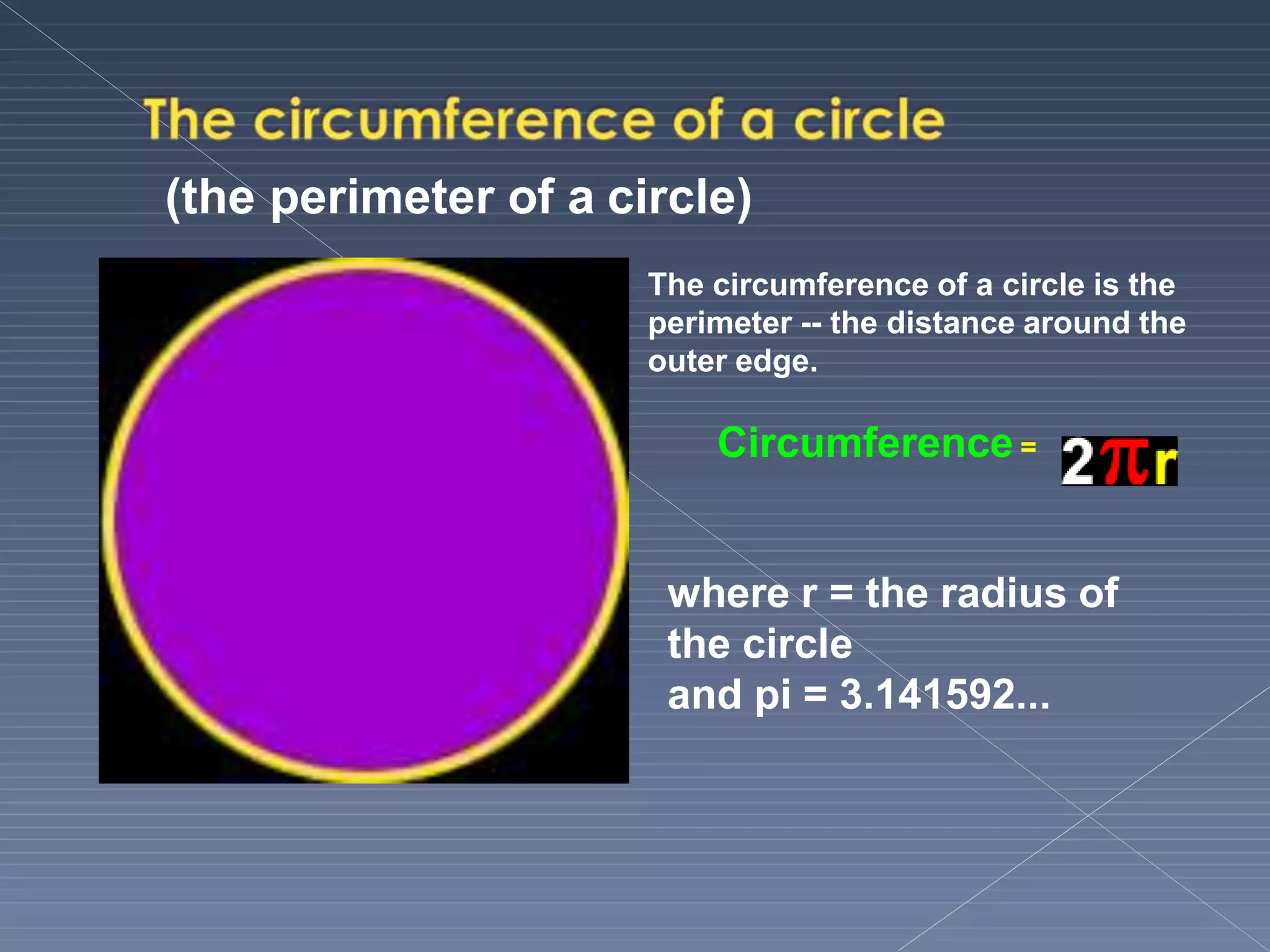
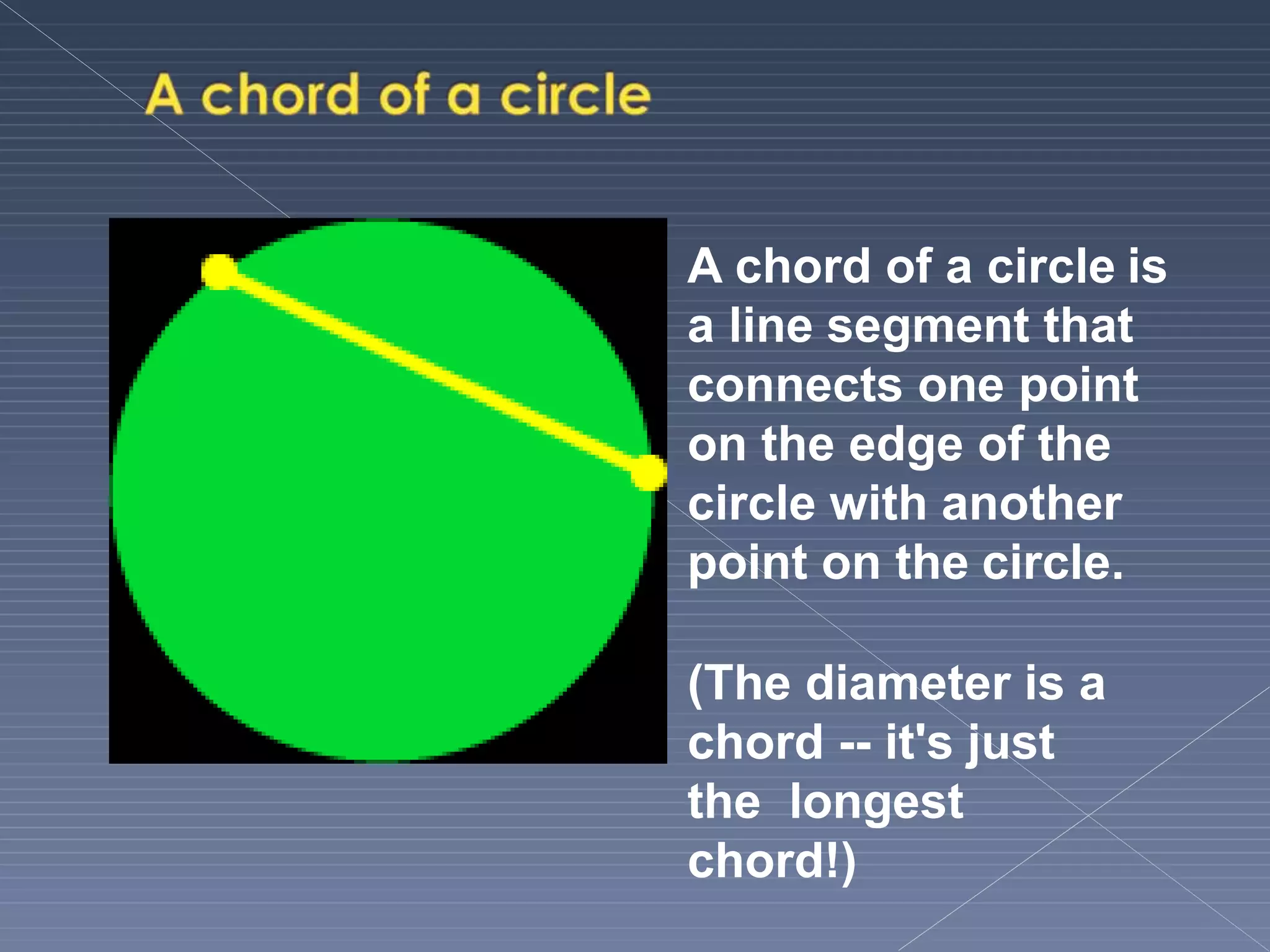
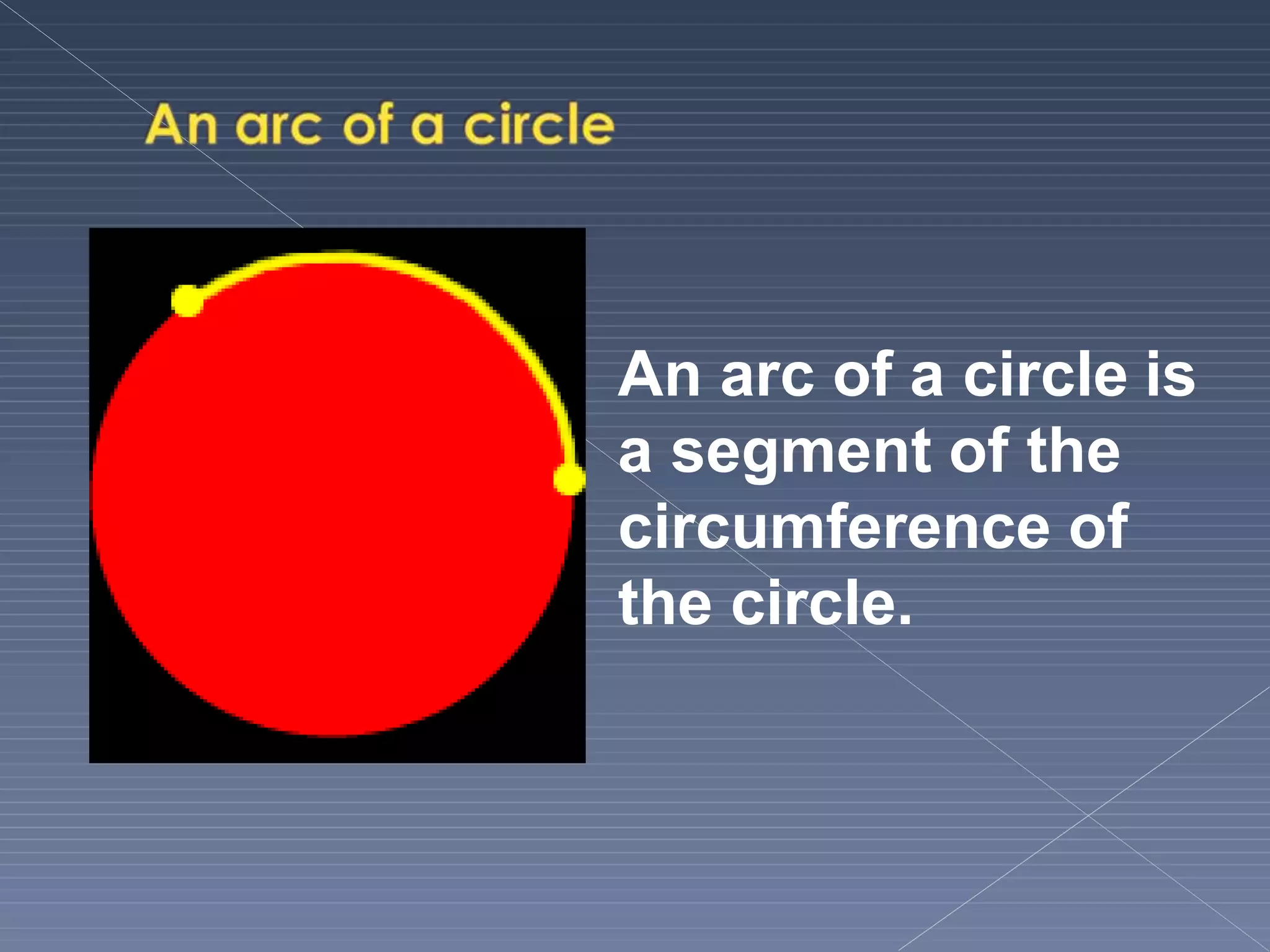
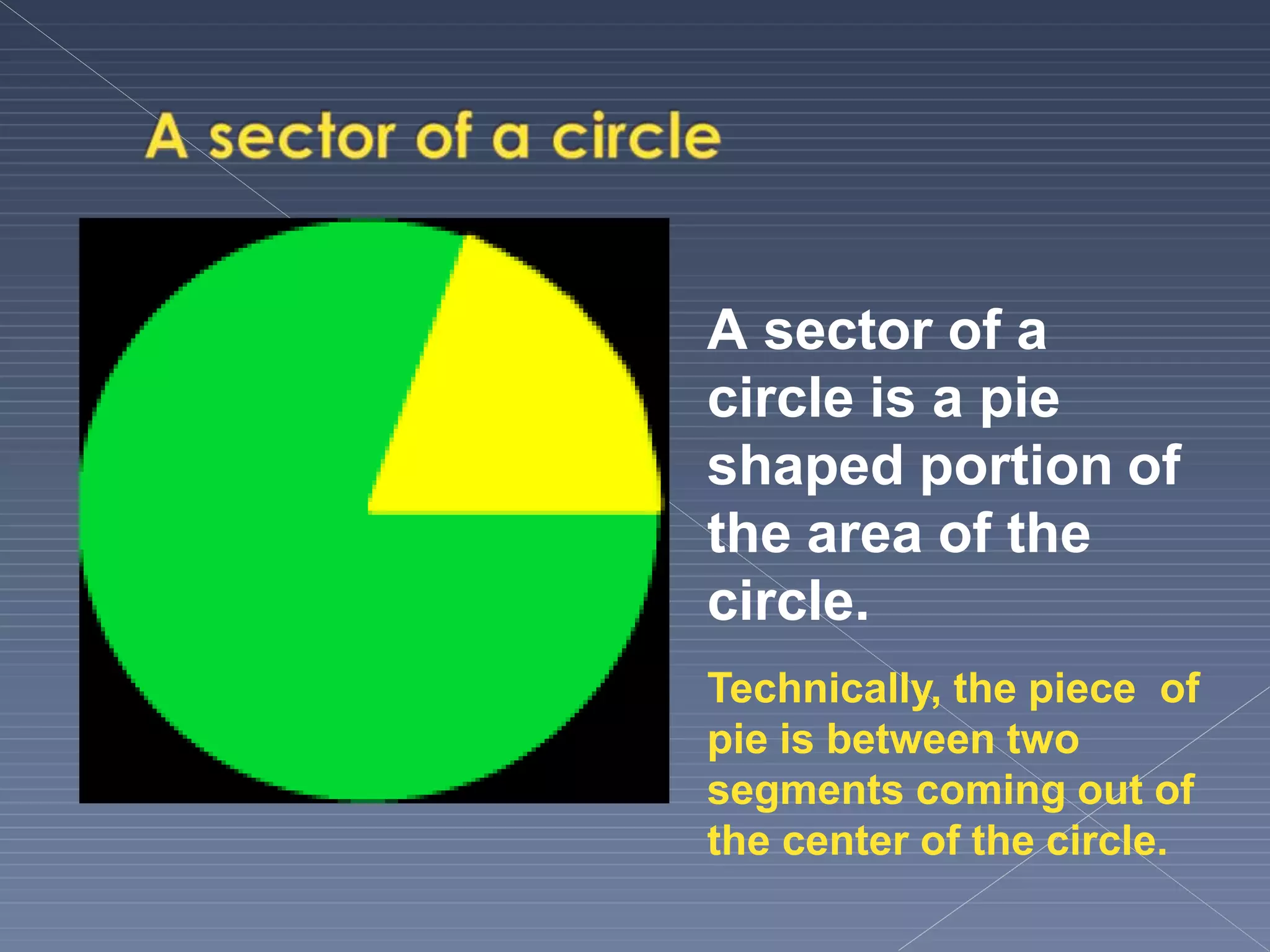
This document defines and explains various geometric terms including: points, lines, rays, line segments, angles, polygons, circles, and their key properties. It discusses how points specify locations, lines can be straight or curved, rays extend from a point, and two rays form an angle. Angles are measured in degrees and can be acute, right, obtuse, complementary or supplementary. Polygons are closed figures made of line segments. Circles have properties like radii, diameters, circumferences, chords, arcs and sectors.

3.  We may think of a
point as a "dot" on a
piece of paper.
 We identify this point
with a number or a
CAPITAL letter.
 A point has no length
or width, it just
specifies an exact
location.

4.  The term
intersect is
used when
lines, rays, line
segments or
figures meet,
that is, they
share a
common
point.
IN THIS CASE THE POINT
OF INTERSECTION IS D

5.  STRAIGHT LINES don’thave a beginning
or an end.
 We usually name these lines with small
letters like r,s,t…
r

6.  We may think of a ray as a straight line
that begins at a certain point and extends
forever in one direction.
B

7.  It has a beginning point and an endpoint
A
B

8.  CURVED
LINES

10. r
r
1

14.  Two rays that share the
same endpoint form an
angle.
 The point where the rays
intersect is called the
vertex of the angle.
 The two rays are called the
sides of the angle.

15.  We usually specify an angle using Greek
letters like these   
 We can also specify an angle with the
letter of its vertex adding the symbol of
angle like this A
A
A

16.  We measure the size of an angle using
degrees.
ACUTE < 90º
RIGHT= 90º
OBTUSE >
90º FLAT =
180º FULL=
360º
CLASIFICATION
BY
MEASUREMENT

17.  Complementary
Angles
: Two angles are
called
complementary
angles if the sum
of their degree
measurements
equals 90 degrees.


  º

18.  Supplementary Angles: Two angles are
called supplementary angles if the sum of
their degree measurements equals 180
degrees.
 º



19.  An angle bisector is a ray
that divides an angle into
two equal angles.

21.  A polygon is a closed figure made by
joining line segments, where each line
segment intersects exactly two others.

22.  The figure below is not a polygon, since it is
not a closed figure:

23.  The figure below is not a polygon, since it is
not made of line segments:

24.  The figure below is not a polygon, since its
sides do not intersect in exactly two
places each:

25.  We’ve got two kinds of polygons:
REGULAR AND IRREGULAR
examples of regular
polygons examples of irregular
polygons

26.  CONVEX POLYGONS: A figure is convex if
every line segment drawn between any two points
inside the figure lies entirely inside the figure.
THESE FUGURES ARE
CONVEX

27.  The following figures are concave. Note
the red line segment drawn between two
points inside the figure that also passes
outside of the figure.
Note the red line segment drawn between two
points inside the figure that also passes outside
the figure.

29. 3 SIDES
(TRIANGLES)
 The sum of the angles of a triangle is 180
degrees.
Equilateral Triangle
A triangle that has three
sides of equal length. The
angles of an equilateral
triangle all measure 60
degrees.

31.  A triangle that has three sides of different
lengths. So therefore, it has three different
angles.

32.  Acute Triangle : A triangle that has three
acute angles.

33. Obtuse Triangle
 A triangle that has an obtuse angle. One of
the angles of the triangle measures more
than 90 degrees.

34. Right Triangle
A triangle that has a right angle. One of the
angles of the triangle measures 90
degrees.

35.  A four-sided polygon. The sum of the
angles of a quadrilateral is 360 degrees.

39. RADIUS
The radius of a circle
is the distance from
the center of the
circle to the outside
edge.

40. The diameter of a circle:
The diameter of a circle
is the longest distance
across a circle. (The
diameter cuts through
the center of the circle.
This is what makes it the
longest distance.)

41. (the perimeter of a circle)
The circumference of a circle is the
perimeter -- the distance around the
outer edge.
Circumference =
where r = the radius of
the circle
and pi = 3.141592...

42. A chord of a circle is
a line segment that
connects one point
on the edge of the
circle with another
point on the circle.
(The diameter is a
chord -- it's just
the longest
chord!)

43. An arc of a circle is
a segment of the
circumference of
the circle.

44. A sector of a
circle is a pie
shaped portion of
the area of the
circle.
Technically, the piece of
pie is between two
segments coming out of
the center of the circle.

45. THANK YOU