Downloaded 424 times
Uploaded byShelly Wilke
Geometric construction
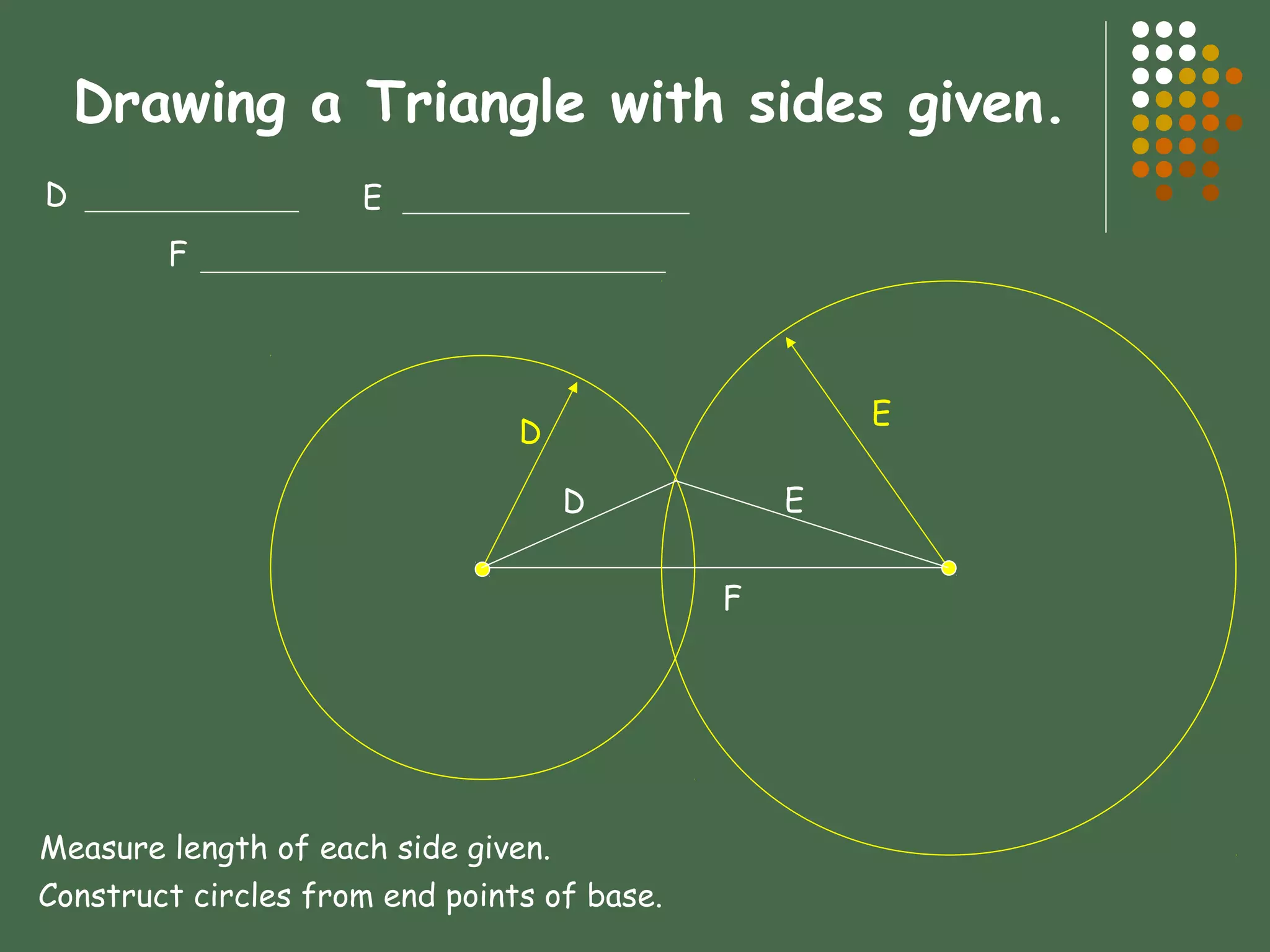
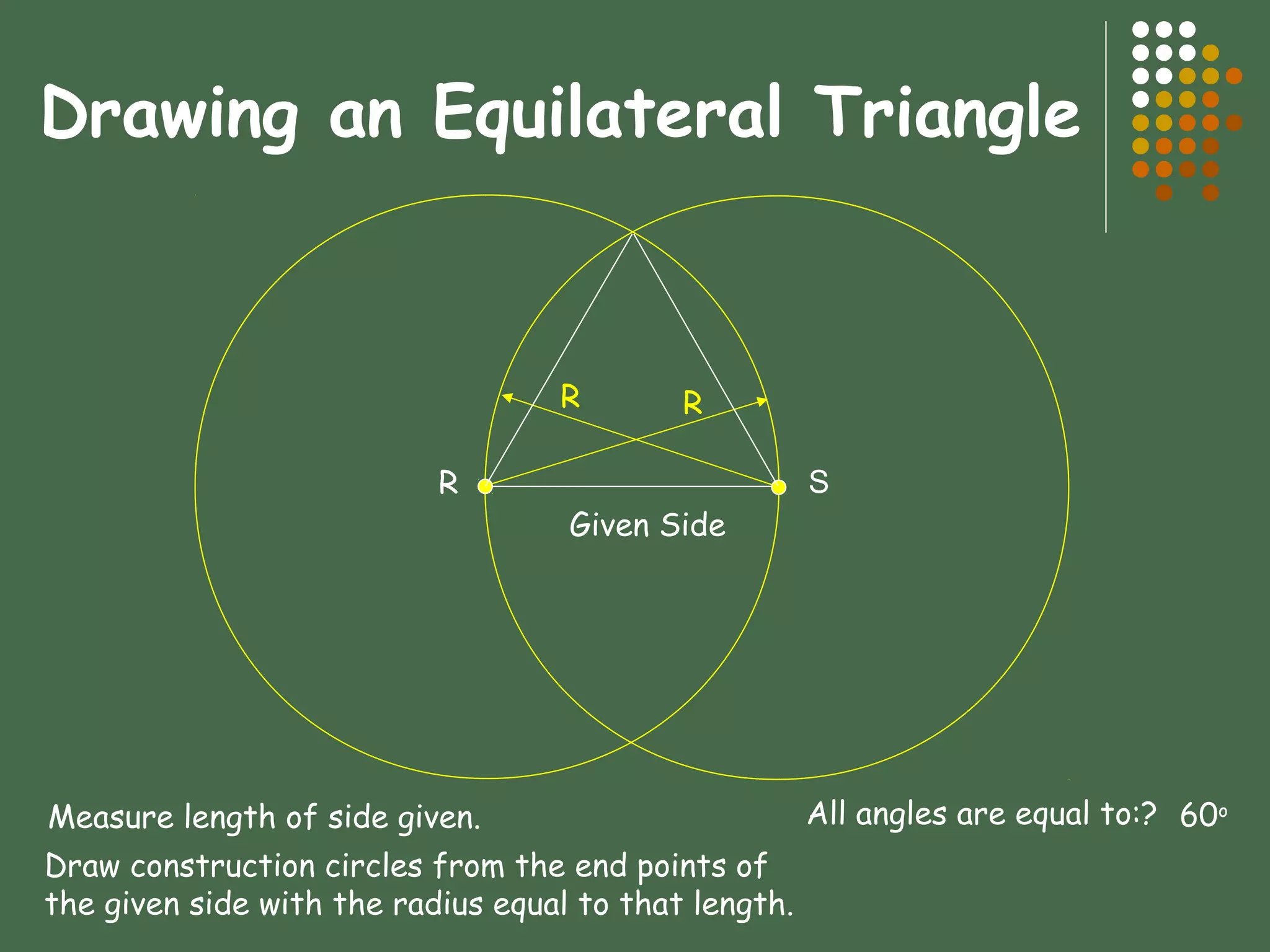
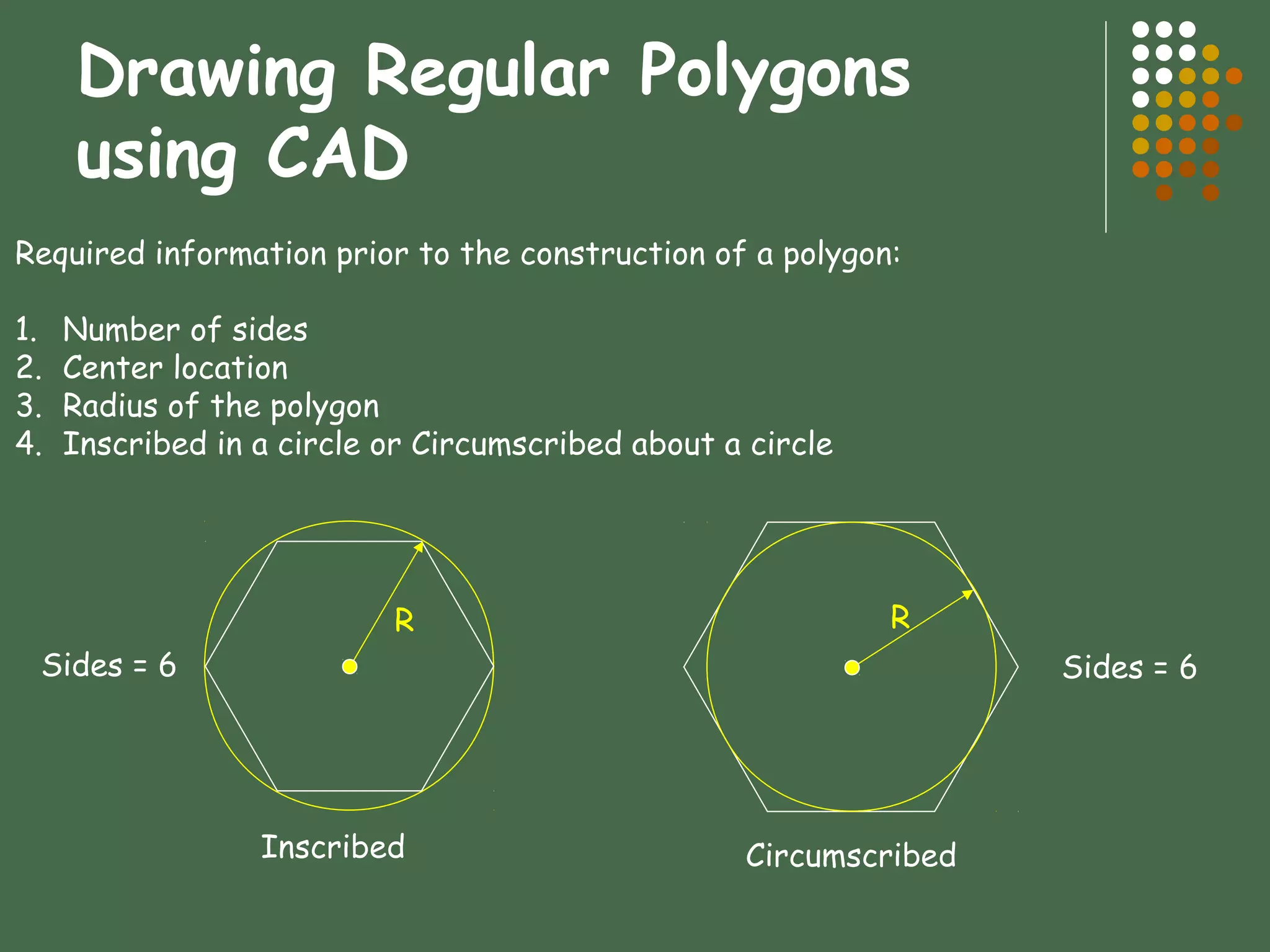
This document provides an overview of geometric constructions. It defines basic geometric elements like points, lines, planes, angles and their properties. It then describes how to construct common geometric shapes like triangles, quadrilaterals, polygons, circles and arcs using compass and straightedge. Specific techniques are presented for drawing shapes given certain parameters, finding bisecting lines and angles, transferring angles, constructing tangents and tangent arcs.
More Related Content
Geometric construction
- 1.
- 2. Point –represents a location in space or on a drawing No height, width, or depth Represented by the intersection of two lines Short cross bar on a line, or A small point element e.g. ( + x l ) Line – is defines as “that which has length without width”1 Straight Line is the shortest distance between two points Lines can be: Parallel – symbol = ll Perpendicular – symbol = Plane – is defined as: 3 points in a space 1 point and an entity with end points e.g. line or arc Points and Lines 1 Defined by Euclid
- 3. Angles Angles areformed by two intersecting lines Common symbol = a 360 Degrees in a full circle (360o ) A degree is divided into 60 minutes (60’) A minute is divided into 60 seconds (60”) Example: 54o 43’ 28” is read 54 degrees, 43 minutes, and 28 seconds. Different kinds of angles are:
- 4. Triangles A triangleis a plane figure bounded by three straight lines and the sum of the interior angles is always 180o . Types of triangles:
- 5. Quadrilaterals A quadrilateralis a plane figure bounded by four straight sides. If the opposite sides are parallel, the quadrilateral is also a parallelogram.
- 6. Polygons A polygonis any plane figure bounded by straight lines. If the polygon has equal angles and equal sides, it can be inscribed or circumscribed around a circle, an is called a regular polygon.
- 7. Circles and Arcs A circle is a closed curve with all points the same distance from a point called the center. Attributes of a circle:
- 8. Bisecting a Lineor Arc B A Construction circles have the same diameter and the radius is equal to more than ½ the length of the line. Given line A-B or Arc A-B Compass Method Midpoint of line
- 9. Bisecting an Angle Givenangle A-B-C Compass Method A C B Initial construction circle drawn at any convenient radius. Second and third circles radius equal to first. Bisector Equal Angles R
- 10. Transferring an Angle CompassMethod X Z Y Initial construction circle drawn at any convenient radius. Second circle radius (R’) equal to first circle radius (R). Y’New Location Given Angle X-Y-Z R R=R’ X’ R’ r r’ Z’ r=r’ Equal Angles Equal Angles
- 11. Drawing a Trianglewith sides given. Measure length of each side given. D F E D E F Construct circles from end points of base. ED
- 12. Drawing a RightTriangle with only two sides given Measure length of each side given. M N R=M R= 1/2 N N Construct a circle = M from one end point of base. M Construct base segment N.
- 13. Drawing an EquilateralTriangle R Given Side S R R Measure length of side given. Draw construction circles from the end points of the given side with the radius equal to that length. All angles are equal to:? 60o
- 14. Drawing Regular Polygons usingCAD Required information prior to the construction of a polygon: 1. Number of sides 2. Center location 3. Radius of the polygon 4. Inscribed in a circle or Circumscribed about a circle R R CircumscribedInscribed Sides = 6 Sides = 6
- 15.
- 16. Drawing a CircleTangent to a Line R G 90 o GivenRadius Given Line Tangent Point Center of Circle Offset
- 17. Drawing a Tangentto Two Circles Tangent Points Tangent Points C1 C2 C1 C2 T T T T
- 18. Tangent to TwoArcs or Circles C1 C2 Only One Tangent Point
- 19. Drawing a TangentArc in a Right Angle Required information prior to the construction of an Arc Tangent to a line: 1. Radius of the desired Arc = R R R R Given Right Angle Offset Offset
- 20. Drawing Tangent Arcs: Acute& Obtuse Angles R R R R R T T T T Acute Angle Obtuse Angle R Required information prior to the construction of an Arc Tangent to a line: Radius of the desired Arc = R Acute Angle Example Obtuse Angle Example Offset Offset Offset Offset
- 21. Arc Tangent to: anArc and a Straight Line RG RD Given Line Required information prior to the construction of an Arc Tangent to a line & Arc: Radius of the desired Arc = RD RD T T Given Arc RG+RD Offset Offset
- 22. Arc Tangent to: anArc and a Straight Line Given Line Required information prior to the construction of an Arc Tangent to a line & Arc: Radius of the desired Arc = RD RD T TRG Given Arc RG-RD RD Offset Offset
- 23. Arc Tangent totwo Arcs Given Arcs RG’ RG Required information prior to the construction of an Arc Tangent to a line & Arc: Radius of the desired Arc = RD T T RD RG+RD RG’+RD Offset Offset
- 24. Arc Tangent totwo Arcs cont. RG’ RG Required information prior to the construction of an Arc Tangent to Two Arcs: Radius of the desired Arc = RD Given Arcs T T RD RG+RD RG’-RD Offset Offset
- 25. Arc Tangent toTwo Arcs cont. Enclosing Both RG RG’ Required information prior to the construction of an Arc Tangent to Two Arcs: Radius of the desired Arc = RD T T Given Arcs RD-RG RD-RG’ RD
- 26. Arc Tangent toTwo Arcs & Enclosing One RG RG’ Required information prior to the construction of an Arc Tangent to Two Arcs: Radius of the desired Arc = RD Given Arcs RD-RG’ RD+RG RD T T Offset
- 27.
- 28. Tangent Arcs –Obtuse Angles Example
- 29. Tangent Arcs –Acute Angles Example
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.