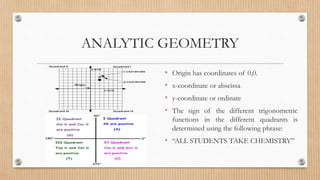
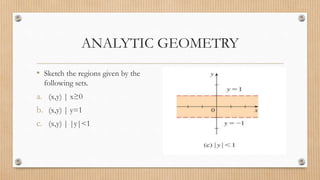
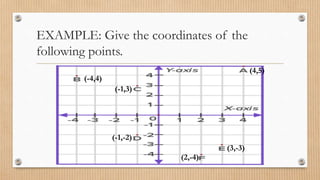
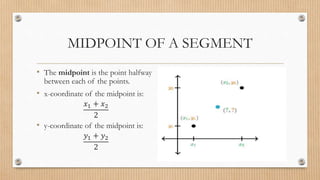
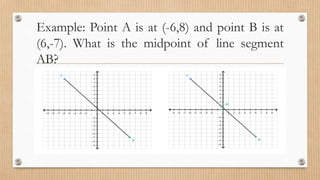
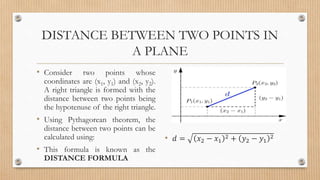
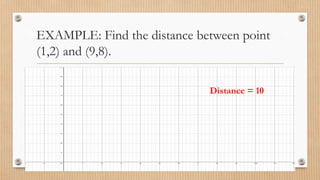
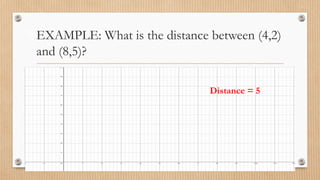
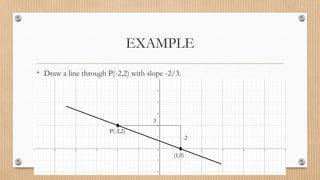
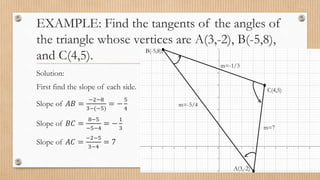
This document provides information about various concepts in analytic geometry including: - Points, lines, planes, line segments, circles, angles, polygons, and their definitions. - Finding midpoints, distances between points, slopes and inclinations of lines. - Calculating slopes, tangents of angles, and the angle between two lines. - Examples are provided to demonstrate finding midpoints, distances, slopes, angles, and solving geometric problems using coordinate systems.

1. ANALYTIC
GEOMETRY
MATH 000 - FINALS

2. GEOMETRY
• Point – has position only. It has no length, width, or thickness.
• Line – is formed by connecting the two points. It is the shortest distance
between two points. It has no length, width, or thickness. It may be straight,
curved or a combination of these.
• Surface – has length and width but no thickness.
• Plane – is a surface such that a straight line connecting any two of its points
lies entirely in it. It is a flat surface.

3. LINE SEGMENT
• A straight line segment is the part of a straight line between two of its
point, including the two points, called endpoint.
• It is designated by the capital letter of these points with a bar over them or
by a small letter. 𝑨𝑩
• It is also known as line segment or segment.

4. LINE SEGMENT
• A line that crosses at the midpoint is said to bisect the segment.
• If 3 points A, B and C lie on a line, then we say they are collinear.
• Two line segments having the same length are said to be congruent

5. EXAMPLE:
• Name each line segment shown in the figure.
• Name the line segment that intersect at A.
• What other line segment can be drawn using points A, B, C and D?
• Name the point of intersection of segment CD and AD.
• Name the point of intersection of segment BC, AC, and CD.

6. CIRCLES
• A circle is the set of all points in a plane that are the same distance from the
center.
• The circumference of a circle is the distance around the circle. It contains
360 degrees.
• A radius is a segment joining the center of a circle to a point on the circle.
• A diameter is a chord through the center of the circle; it is the longest chord
and is twice the length of the radius.

7. CIRCLES
• A chord is a segment joining any two points on a circle.
• A semicircle is an arc measuring one-half of the circumference of a circle
and thus contain 180 degree.
• An arc is a continuous part of a circle.
• A central angle is an angle formed by two radii.

8. EXAMPLE:
• Find OC and AB
OC= 12
AB=24
• Find the number of degrees in arc AD
AD=80º
• Find the number of degrees in arc BC
BC=110º
C
D
A B
70º
100º
12
O

9. ANGLES
• An angle is the figure formed by two rays with a common end point.
• The rays are the sides of the angle, while the end point is the vertex.
• Perpendiculars are lines or rays or segment that meet at right angles.
• A perpendicular bisector of a given segment is perpendicular to the
segment and bisects it.

10. POLYGON
• A polygon is a closed plane figure bounded by straight line segments as side.
• A pentagon is a polygon of five sides.
• A quadrilateral is a polygon having four sides.
• A triangle is a polygon having three sides.
• A vertex of a triangle is a point at which two of the sides meet

11. TRAPEZOID
• A trapezoid is a quadrilateral having two, and only two, parallel sides.
• The bases of the trapezoid are its parallel side.
• The legs are its non parallel side.
• The median of the trapezoid is the segment joining the midpoints of its
legs.

12. PARALLELOGRAMS
• A parallelogram is a quadrilateral whose opposite sides
are parallel.
• A rectangle is an equiangular parallelogram.
• A rhombus is an equilateral parallelogram.
• A square is an equilateral and equiangular parallelogram.

13. ANALYTIC GEOMETRY
ANALYTIC GEOMETRY – deals with geometric problems using coordinates
system thereby converting it into algebraic problems.
RENE DESCARTES (1596 – 1650, Cartesius in Latin language) – is regarded
as the founder of analytic geometry by introducing coordinates system in 1637.
RECTANGULAR COORDINATES SYSTEM – also known as CARTESIAN
COORDINATE SYSTEM

14. ANALYTIC GEOMETRY
• A number line is a line on which distances from a point are marked off in
equal units, positively in one direction and negatively in the other.
• The graph is formed by combining two number line at right angles to each
other so that their zero points coincide.
• The quadrants of a graph are the four parts cut off by the axes.

15. ANALYTIC GEOMETRY
• Origin has coordinates of 0,0.
• x-coordinate or abscissa
• y-coordinate or ordinate
• The sign of the different trigonometric
functions in the different quadrants is
determined using the following phrase:
• “ALL STUDENTS TAKE CHEMISTRY”

16. ANALYTIC GEOMETRY
• Sketch the regions given by the
following sets.
a. (x,y) | x≥0
b. (x,y) | y=1
c. (x,y) | |y|<1

17. EXAMPLE: Give the coordinates of the
following points.
(4,5)
(-4,4)
(-1,3)
(-1,-2)
(3,-3)
(2,-4)

18. EXAMPLE: If the vertices of a rectangle have
the coordinates A(3,1), B(-5,1), C(-5,-3) and
D(3,-3), find its perimeter and area.
• Perimeter=2(b+h)
• Perimeter=2(8+4)
• Perimeter=24
• Area=bh
• Area=8*4
• Area=32

19. MIDPOINT OF A SEGMENT
• The midpoint is the point halfway
between each of the points.
• x-coordinate of the midpoint is:
𝑥1 + 𝑥2
2
• y-coordinate of the midpoint is:
𝑦1 + 𝑦2
2

20. Example: Point A is at (-6,8) and point B is at
(6,-7). What is the midpoint of line segment
AB?

21. EXAMPLE:
• Find the midpoint of (5,3)
and (1,7).
• Midpoint=(3,5)
• What is the midpoint of
(6,2) and (10,0)?
• Midpoint=(1,8)

22. ANALYTIC GEOMETRY
• A line on which one direction is chosen as positive and the opposite direction as
negative is called a directed line.
• A segment of the line, consisting of any two points and the part between is called a
directed line segment
• Undirected distance is the length of the segment, which we take as positive.
• The absolute value of a real number a, denoted by |a|, is the real number such
that |a|=a when a is positive or zero, |a|= -a when a is negative.
• Real numbers consist of the positive numbers, the negative numbers, and zero.

23. DISTANCE BETWEEN TWO POINTS IN
A PLANE
• Consider two points whose
coordinates are (x1, y1) and (x2, y2).
A right triangle is formed with the
distance between two points being
the hypotenuse of the right triangle.
• Using Pythagorean theorem, the
distance between two points can be
calculated using:
• This formula is known as the
DISTANCE FORMULA
• 𝑑 = 𝑥2 − 𝑥1
2 + 𝑦2 − 𝑦1
2

24. EXAMPLE: Find the distance between point
(1,2) and (9,8).
Distance = 10

25. EXAMPLE: What is the distance between (4,2)
and (8,5)?
Distance = 5

26. INCLINATION AND SLOPE OF A LINE
• The inclination of a line is a concept used extensively in calculus and other
areas of mathematics.
• The inclination of a line that intersects the axis is the smallest angle, greater
than or equal to 0°. That the line makes with the positive direction of the x-
axis. The inclination of a horizontal line is 0.
• The slope of a line is the tangent of the inclination.

27. SLOPE OF A LINE
• The slope of the line is defined as the rise (vertical) per run (horizontal).
• 𝑠𝑙𝑜𝑝𝑒 =
𝑟𝑖𝑠𝑒
𝑟𝑢𝑛
=
∆𝑦
∆𝑥
= tan Ɵ
• Where: ∆ denotes an increment
• 𝑚 =
𝑦2−𝑦1
𝑥2−𝑥2
∴The line whose equation is y = 𝑚𝑥 + 𝑏 has slope 𝑚

28. INCLINATION AND SLOPE OF A LINE
• Slope = 0
• Slope = positive
• Slope = negative
• Slope = infinity

29. EXAMPLE
• Draw a line through P(2,2) with inclination 35°.
P(2,2) 35°
35°

30. EXAMPLE
• Draw a line through P(-2,2) with slope -2/3.
P(-2,2)
-2
3
(1,0)

31. EXAMPLE
• Find the slope of the line through (-2,-1) and (4,3).
• Slope=2/3
• Find the slope of the line whose equation is 3y-4x=15.
• Slope=4/3
• Find the inclination of the line whose equation is y=x+4.
• Ɵ=45 degree

32. ANGLE BETWEEN TWO LINES
• Two intersecting lines form two pairs of equal angles, and an angle of one pair is
the supplement of an angle of the other pair.
• Recalling that an exterior angle of a triangle is equal to the sum of the remote
interior angles, we see that ∅ + Ɵ1 = Ɵ2 𝑜𝑟 ∅ = Ɵ2 − Ɵ1.
• Using the formula for the tangent of the difference of two angles, we find
tan ∅ =
𝑚2−𝑚1
1+𝑚1𝑚2
• where 𝑚2 is the slope of the terminal side and 𝑚1is the slope of the initial side.

33. EXAMPLE: Find the tangents of the angles of
the triangle whose vertices are A(3,-2), B(-5,8),
and C(4,5).
Solution:
First find the slope of each side.
Slope of 𝐴𝐵 =
−2−8
3−(−5)
= −
5
4
Slope of 𝐵𝐶 =
8−5
−5−4
= −
1
3
Slope of 𝐴𝐶 =
−2−5
3−4
= 7
A(3,-2)
B(-5,8),
C(4,5)
m=-1/3
m=-5/4
m=7

34. EXAMPLE: Find the tangents of the angles of
the triangle whose vertices are A(3,-2), B(-5,8),
and C(4,5).
Solution:
tan 𝐴 =
−
5
4
− 7
1 + −
5
4
7
tan 𝐴 =
33
31
𝐴 = 47°
tan 𝐵 =
−
1
3
− −
5
4
1 + −
1
3
−
5
4
tan 𝐴 =
11
17
B= 33°
tan 𝐶 =
7 − −
1
3
1 + 7 −
1
3
tan 𝐶 = −
22
4
B= −5.5°