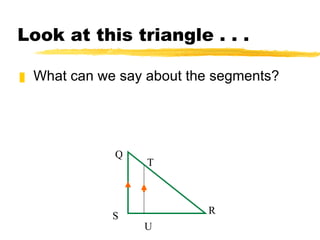
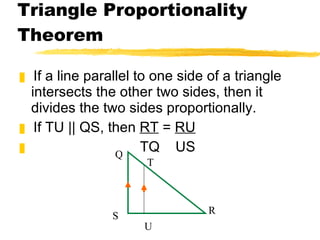
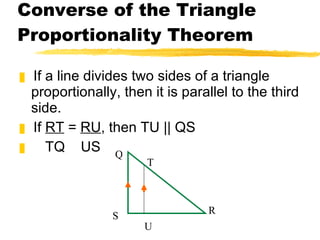
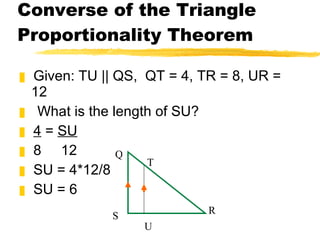
This document discusses proportionality theorems that can be used to calculate unknown segment lengths in triangles. It introduces the Triangle Proportionality Theorem and its converse, which state that if a line parallel to one side of a triangle intersects the other two sides, it divides them proportionally. An example problem demonstrates using these theorems to find the length of segment SU given other segment lengths and that TU is parallel to QS. Additional proportional theorems and practice problems are also presented.

1. Proportions and Similar Triangles Objectives: Use proportionality theorems to calculate segment lengths

2. Look at this triangle . . . What can we say about the segments? Q T S U R

3. Triangle Proportionality Theorem If a line parallel to one side of a triangle intersects the other two sides, then it divides the two sides proportionally. If TU || QS, then RT = RU TQ US Q T S U R

4. Converse of the Triangle Proportionality Theorem If a line divides two sides of a triangle proportionally, then it is parallel to the third side. If RT = RU , then TU || QS TQ US Q T S U R

5. Converse of the Triangle Proportionality Theorem Given: TU || QS, QT = 4, TR = 8, UR = 12 What is the length of SU? 4 = SU 8 12 SU = 4*12/8 SU = 6 Q T S U R

6. More Theorems - see p. 499 If 3 parallel lines intersect two transversals, then they divide the transversals proportionally. If a ray bisects an angle of a triangle, then it divides the opposite side into segments whose lengths are proportional to the lengths of the other 2 sides.

7. Try some . . . Do Example 5, p. 501 Do Example 6, p. 501 Do p. 502 1-10 Do p. 503 #29 Do p. 504 #36

8. Homework Do worksheets