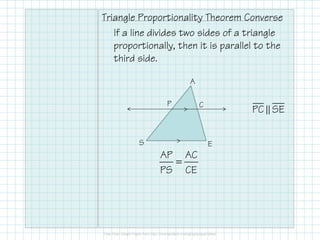
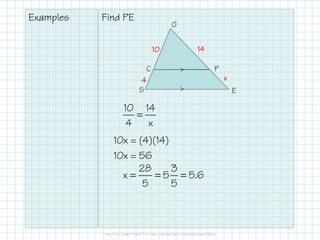
The document outlines properties and theorems related to similar triangles, including the triangle proportionality theorem and its converse, which state that if a line is parallel to a side of a triangle, it divides the other sides proportionally. It also discusses the concept of transversal proportionality when parallel lines intersect transversals. Various examples illustrate the application of these concepts in finding segment lengths and verifying proportional relationships.

1. Obj. 36 Similar Triangle Properties
The student is able to (I can):
• Use properties of similar triangles to find segment
lengths.
• Apply proportionality and triangle angle bisector
theorems.

2. Triangle Proportionality Theorem
If a line parallel to a side of a triangle
intersects the other two sides then it
divides those sides proportionally.
A
P
S
>
>
AP AC
=
PS CE
C
E
PC SE
Note: This ratio is not the same as the
ratio between the third sides!
AP PC
≠
PS SE

3. Triangle Proportionality Theorem Converse
If a line divides two sides of a triangle
proportionally, then it is parallel to the
third side.
A
P
S
>
>
AP AC
=
PS CE
C
PC SE
E

4. Two Transversal Proportionality
If three or more parallel lines intersect
two transversals, then they divide the
transversals proportionally.
C
A
T
>
>
>
CA DO
=
AT OG
D
O
G

5. Examples
Find PE
O
14
10
C
4
S
>
P
x
>
10 14
=
4
x
10x = (4)(14)
10x = 56
28
3
x=
= 5 = 5.6
5
5
E

6. Example
Verify that HE OS
H
15
O
10
E
12
S
8
R
15 10
= ?
12 8
(15)(8) = (10)(12)?
120 = 120
Therefore, HE OS

7. Example
Solve for x.
>
x
10
>
6
10 x
=
6 9
6x = (10)(9)
6x = 90
x = 15
>
9