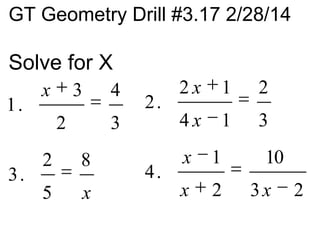1. The document provides instructions and objectives for geometry drill 3.17, which includes solving ratios and proportions to find unknown values. 2. It also contains examples of using ratios and proportions to find missing angle measures in a triangle given the ratio of the existing angles, and examples of setting up and solving proportions to find unknown side lengths when given a scale drawing. 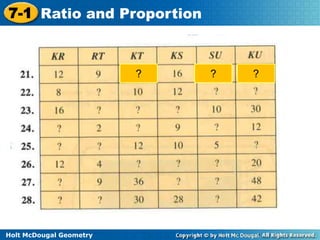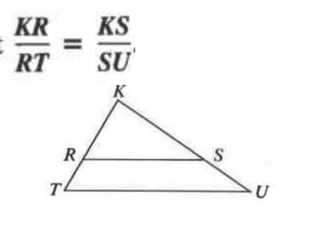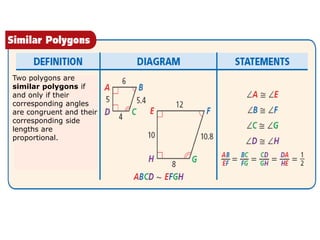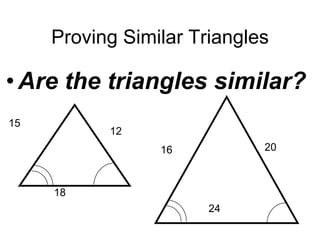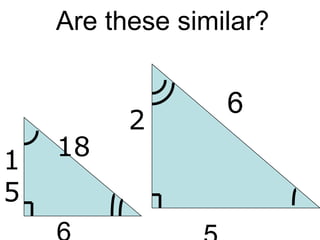3. Key concepts covered include ratios, proportions, similar polygons, scale factors, and using properties of proportions to solve problems involving similar figures.

1. GT Geom Drill 3.17
1. Take out HW and a pen and put it
on the corner of your desk.
2. Objective:
STW write and simplify ratios and use
proportions to solve problems.
STW discover properties of similar polygons

2. GT Geometry Drill #3.17 2/28/14
Solve for X
1.
x
3
2
3.
4
3
2
8
5
x
4.
1
2
4x
2.
2x
1
3
x
1
x
2
10
3x
2

3. GT Geometry Drill #3.17 2/28/14
5. The ratio of the side lengths of a triangle is
4:7:5, and its perimeter is 96 cm. What is the
length of the shortest side?
Let the side lengths be 4x, 7x, and 5x.
Then 4x + 7x + 5x = 96 . After like terms are
combined, 16x = 96. So x = 6. The length of the
shortest side is 4x = 4(6) = 24 cm.
6. The ratio of the angle measures in a
triangle is 1:6:13. What is the measure of
each angle?

4. 7-1 Ratio and Proportion
The ratio of the angle measures in a triangle is
1:6:13. What is the measure of each angle?
x + y + z = 180°
x + 6x + 13x = 180°
20x = 180°
x = 9°
y = 6x
z = 13x
y = 6(9°)
z = 13(9°)
y = 54°
z = 117°
Holt McDougal Geometry

5. 7-1 Ratio and Proportion
?
Holt McDougal Geometry
?
?

6. 7-1 Ratio and Proportion
21
6
8
2
8
4
27
20 10
Holt McDougal Geometry
24
8
16
20
12
3
28
15
3
15
15
36
5
12
14

8. 7-1 Ratio and Proportion
Example 4: Using Properties of Proportions
Given that 18c = 24d, find the ratio of d to c in
simplest form.
18c = 24d
Divide both sides by 24c.
Simplify.
Holt McDougal Geometry

9. 7-1 Ratio and Proportion
Check It Out! Example 4
Given that 16s = 20t, find the ratio t:s in
simplest form.
16s = 20t
Divide both sides by 20s.
Simplify.
Holt McDougal Geometry

10. 7-1 Ratio and Proportion
Example 5: Problem-Solving Application
Marta is making a scale drawing of her
bedroom. Her rectangular room is 12 feet
wide and 15 feet long. On the scale
drawing, the width of her room is 5 inches.
What is the length?
1
Understand the Problem
The answer will be the length of the room
on the scale drawing.
Holt McDougal Geometry

11. 7-1 Ratio and Proportion
Example 5 Continued
2
Make a Plan
Let x be the length of the room on the scale
drawing. Write a proportion that compares
the ratios of the width to the length.
Holt McDougal Geometry

12. 7-1 Ratio and Proportion
Example 5 Continued
3
Solve
5(15) = x(12.5) Cross Products Property
75 = 12.5x
x=6
Simplify.
Divide both sides by 12.5.
The length of the room on the scale drawing
is 6 inches.
Holt McDougal Geometry

13. Agree or Disagree
1. If two figures are similar then they are congruent
2. If the ratios of the length of corresponding sides of two
triangles are equal, then the triangles are congruent.
3. If triangles are similar then they have the same shape
4. If two triangles are congruent then each pair of
corresponding angles are congruent.
5. If two angles of one triangle are congruent to corresponding
angles of another triangle, then the triangles are similar

14. Vocabulary
similar
similar polygons
similarity ratio

15. Figures that are similar (~) have the same shape
but not necessarily the same size.

16. Two polygons are
similar polygons if
and only if their
corresponding angles
are congruent and their
corresponding side
lengths are
proportional.

17. Proving Similar Triangles
• Are the triangles similar?
15
12
20
16
18
24

18. Are these similar?
1
5
18
2
6

19. Scale Factor
The ratio of the lengths
of two corresponding
sides of similar
polygons.