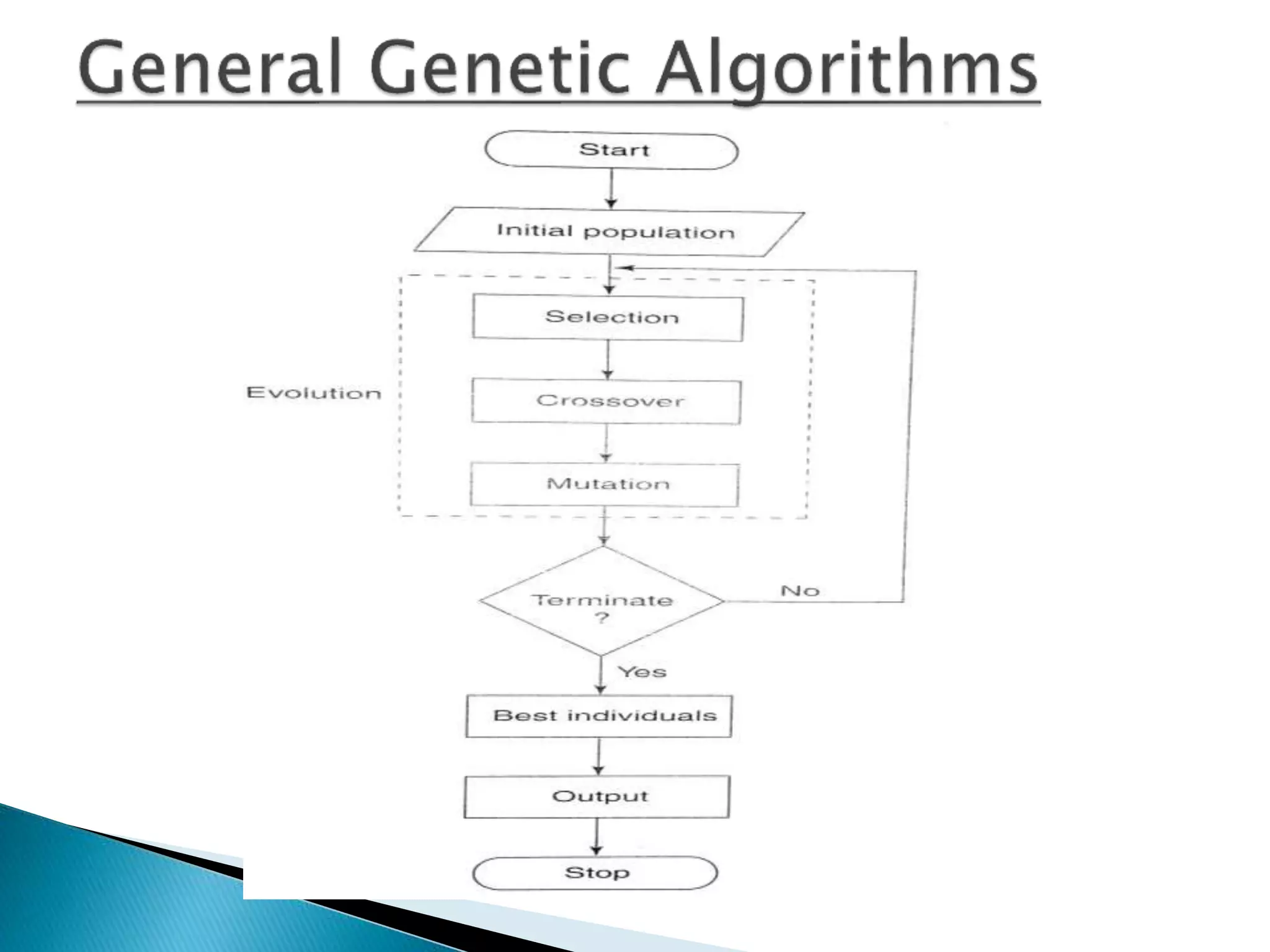
Genetic algorithms are heuristic search methods inspired by natural selection that can be used to find optimized solutions to problems. They work by generating an initial random population of solutions and then applying genetic operations like selection, crossover and mutation to produce new solutions over multiple generations. The fittest solutions survive and weaker ones die out, causing the overall population to become better adapted to the problem being solved. Genetic algorithms are well-suited for searching large, complex datasets and problems with multimodal or n-dimensional search spaces.

1. Application of genetic algorithm in machine
learning
Submitted
By:
Jagadish Mohanty
1721109165
th

2.  Introduction of GAs
 Why genetic algorithm
 Basic terminology
 Flow chat
 Procedure
 Fitness function
 Genetic operations
a. Selection Operation
b. Crossover Operations
 Single-Point Crossover
 Two-Point Crossover
 Uniform Crossover
c. Mutation Operations
 Example of MAXONE problem
 Conclusion
 References

3.  The basic techniques of the genetic algorithms are
designed to simulate processes in natural system
necessary for evolution, especially those follow that
principles first laid down by Charles Darwin. ”survival
of the fittest,” because in nature, competition among
individuals for scanty resources results in the fittest
individuals dominating over the weaker ones.
 A genetic algorithm is a heuristic search method used
in artificial intelligence and computing.
 It is used for finding optimized solutions to search
problems based on the theory of natural selection
and evolutionary biology.
 Genetic algorithms are excellent for searching
through large and complex data sets.

4.  They are better than conventional algorithms
in that they are more robust. Unlike older AI
systems, they do not break easily even if the
inputs are changed slightly or in the presence
of reasonable noise.
 Also in searching a large state space
multimodal state-space or n-dimensional
surface, a GA may offer significant benefits
over more typical optimization techniques.

5.  Population-subset of all
the possible solutions
to the given problem.
 Chromosomes-one
such solution to given
problem
 Gene- one element
position of a
chromosome.
 Allele- value a gene
takes for particular
chromosome.

6.  Genotype- population in
the computation space.
 Phenotype- population
in the actual real world
solution space.
 Decoding- transforming
a solution from the
genotype to the
phenotype space.
 Encoding- transforming
from the phenotype to
genotype space

8. {
1. [Start] Generate random population of n chromosomes (suitable solutions for the
problem).
2. [Fitness] Evaluate the fitness f(x) of each chromosome x in the population.
3. [New population] Create a new population by repeating following steps until the
new population is complete
a. [Selection] Select two parent chromosomes from a population according to their
fitness (the better fitness, the bigger chance to be selected).
b. [Crossover] With a crossover probability cross over the parents to form a new
offspring (children). If no crossover was performed, offspring is an exact copy of
parents.
c. [Mutation] With a mutation probability mutate new offspring at each locus
(position in chromosome).
d. [Accepting] Place new offspring in a new population.
4. [Replace] Use new generated population for a further run of algorithm.
5. [Test] If the end condition is satisfied, stop, and return the best solution in current
population.
6. [Loop] Go to step 2.
}

9.  The fitness function defines the criterion for ranking
potential hypotheses and for probabilistically selecting
them for inclusion in the next generation population. If the
task is to learn classification rules, then the fitness
function typically has a component that scores the
classification accuracy of the rule over a set of provided
training examples.
 Often other criteria may be included as well, such as the
complexity or generality of the rule. More generally, when
the bit-string hypothesis is interpreted as a complex
procedure (e.g., when the bit string represents a collection
of if-then rules that will be chained together to control a
robotic device), the fitness function may measure the
overall performance of the resulting procedure rather than
performance of individual rules.

10.  Selection operation is to select elitist
individuals as parents in current
population, which can generate offspring.
Fitness values are used as criteria to judge
whether individuals are elitist.
 There are many methods how to select the
best chromosomes, for example roulette
wheel selection, rank selection, elitism
selection and some others.

11. 1. Single-Point Crossover
 A cross site is selected randomly along the
length of the mated strings
 Bits next to the cross site are exchanged
 If good strings are not created by crossover,
they will not beyond next generation.
1 0 1 1 1 1 1 1
0 1 0 1 0 0 0 1 0 1 0 1 0 1 1 1
1 0 1 1 1 0 0 1Parent 1
Parent 2
Strings before mating
Offspring 1
Offspring 2
String after mating

12.  Two random sites are chosen.
 The contents bracketed by these are
exchanged between two mated parents.
1 0 0 1 0 1 1 1
0 1 1 1 0 0 0 1 0 1 1 1 0 1 0 1
1 0 0 1 0 0 1 1Parent 1
Parent 2
Strings before mating
Offspring 1
Offspring 2
String after mating

13.  Bits are randomly copied from the first or
from the second parent.
 A random mask is generated.
 The mask determines which bits are copied
from one parent and which from the other
parent.
 Mask: 0110011000 (Randomly generated)
Parent 1 1 0 1 0 0 0 1 1 1 0
Parent 2 0 0 1 1 0 1 0 0 1 0
Offspring 1 0 0 1 1 0 0 1 0 1 0
Offspring 2 1 0 1 0 0 1 0 1 1 0

14.  In addition to recombination operators that
produce offspring by combining parts of two
parents, a second type of operator produces
offspring from a single parent.
 In particular, the mutation operator produces
small random changes to the bit string by
choosing a single bit at random, then
changing its value.

15.  We start with a population of n random
strings. Suppose that l=10 and n=6
 We toss a fair coin 60 times and get the
following initial population:
S1= 1111010101
S2= 0111000101
S3= 1110110101
S4= 0100010011
S5= 1110111101
S6= 0100110000

16. 20.58%
14.70%
20.58%
11.76%
23.52%
08.82%
Selection

17.  Suppose that, after performing selection, we
get the following population.
20.58
14.7
20.58
11.76
23.52
8.82
Selection
S1 S2 S3 S4 S5 S6

18.  Before crossover:
S1’=1111010101 S5’=0100010011
S2’=1110110101 S6’=1110111101
 After crossover:
S1’’=1110110101 S5’’=0100011101
S2’’=1111010101 S6’’=1110110011

19.  Before Mutation
S1’’=1110110101
S2’’=1111010101
S3’’=1110111101
S4’’=0111000101
S5’’=0100011101
S6’’=1110110011
 After Mutation
S1’’’=1110100101
S2’’’=1111110100
S3’’’=1110101111
S4’’’=0111000101
S5’’’=0100011101
S6’’’=1110110001

20.  After Applying Mutation
S1’’’=1110100101 f(S1’’’)=6
S2’’’=1111110100 f(S2’’’)=7
S3’’’=1110101111 f(S3’’’)=8
S4’’’=0111000101 f(S4’’’)=5
S5’’’=0100011101 f(S5’’’)=5
S6’’’=1110110001 f(S6’’’)=6
-------------------------------
∑f=37

21.  In one generation, the total population fitness
changed from 34 to 37.
 At this point we go through the same process
all over again, until a stopping criterion is
met.
 In each iteration number of 1’s will maximize
either to a particular threshold value or to the
maximum value i.e. 60 in this example.

22. ◦ Genetic algorithms are excellent for searching through
large and complex data sets.
◦ Genetic algorithm is a heuristic search method used in
artificial intelligence and computing.

23.  https://www.researchgate.net/publication/30
9770246
 https://www.slideshare.net/zamakhan/geneti
c-algorithms-6229473
 https://m.youtube.com/watch?v=f0bGSPo5aJ
k
 https://www.researchgate.net/publication/26
7369803
 www.cs.bgu.ac.il/~assafza