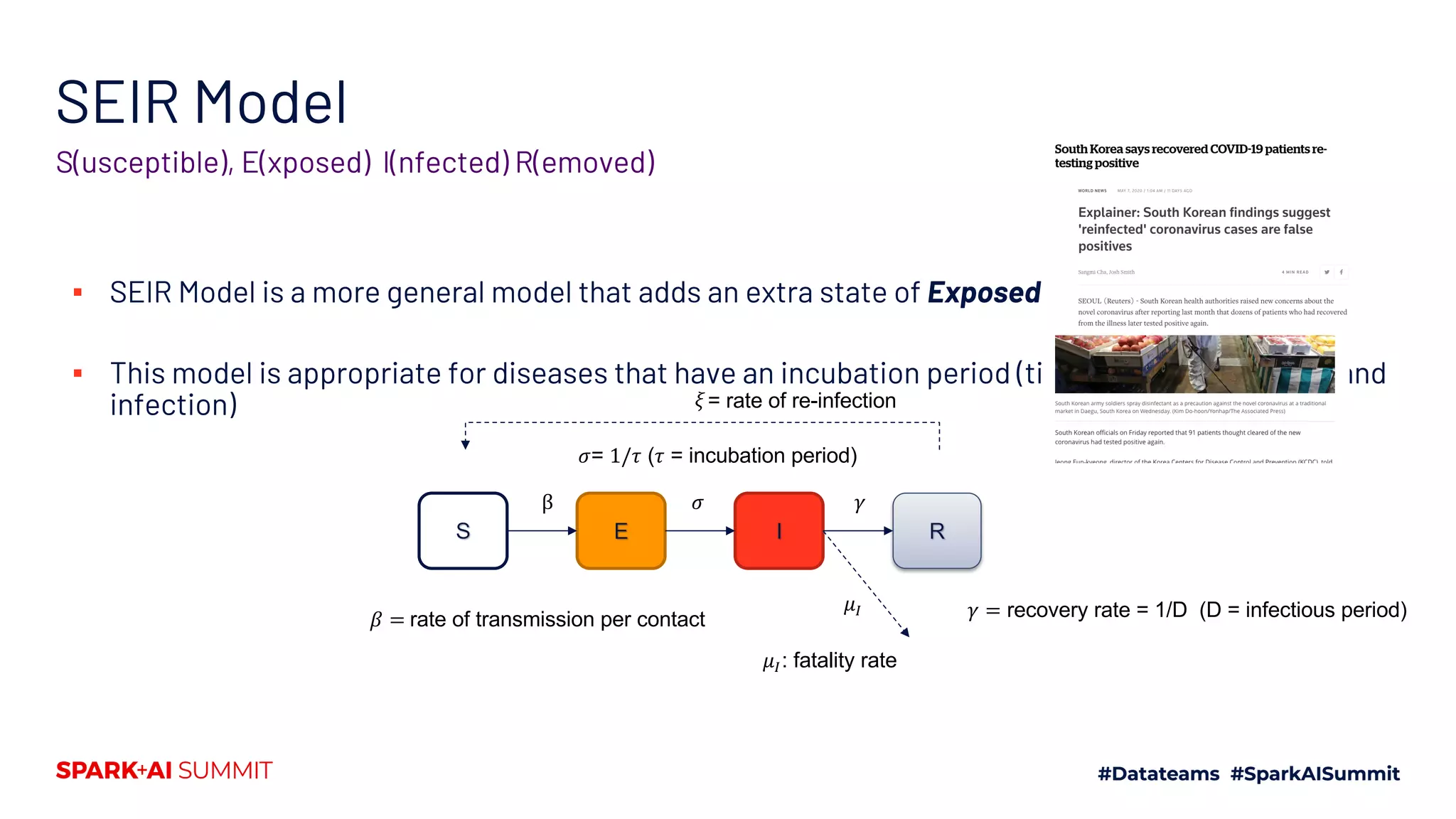
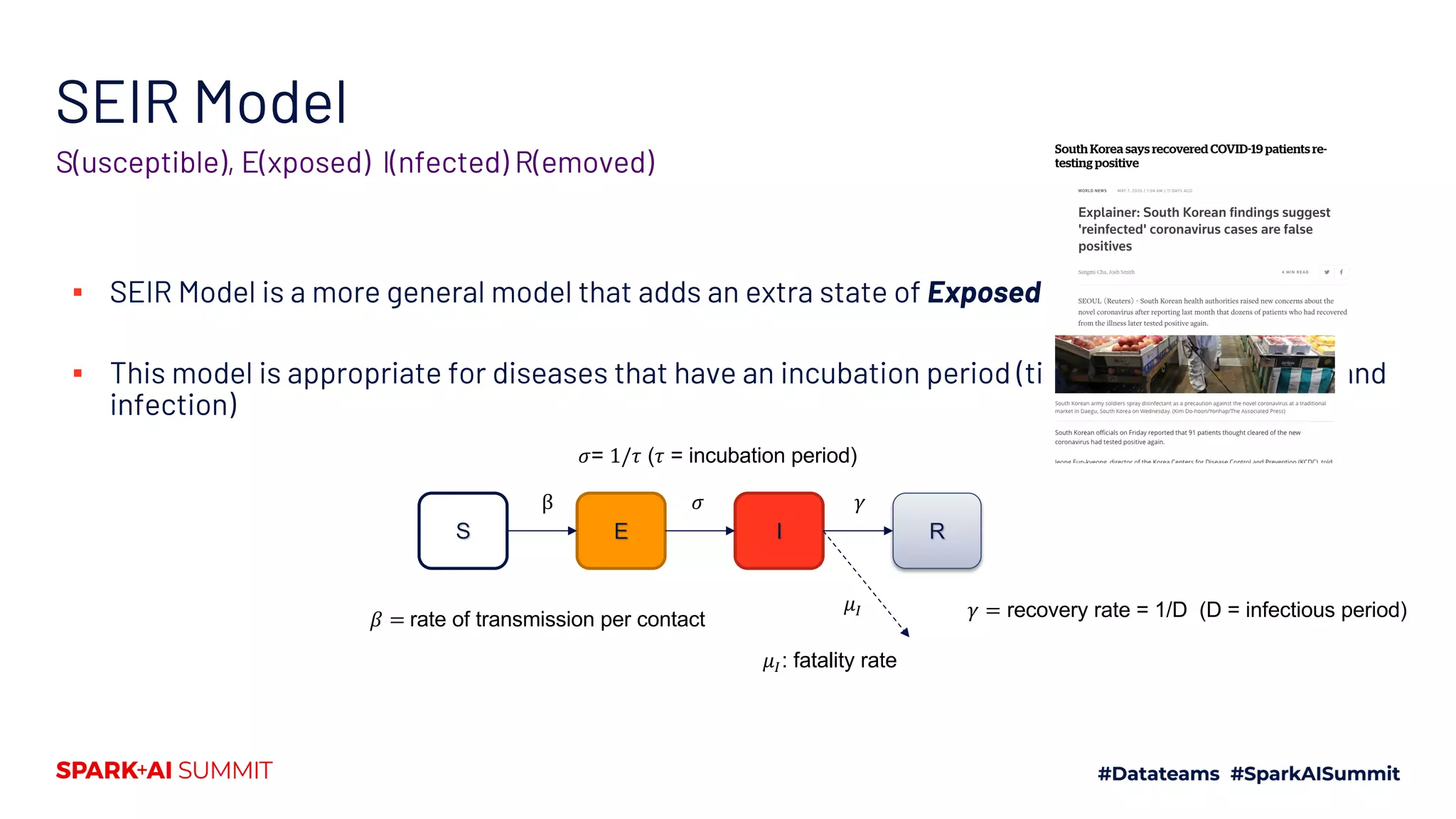
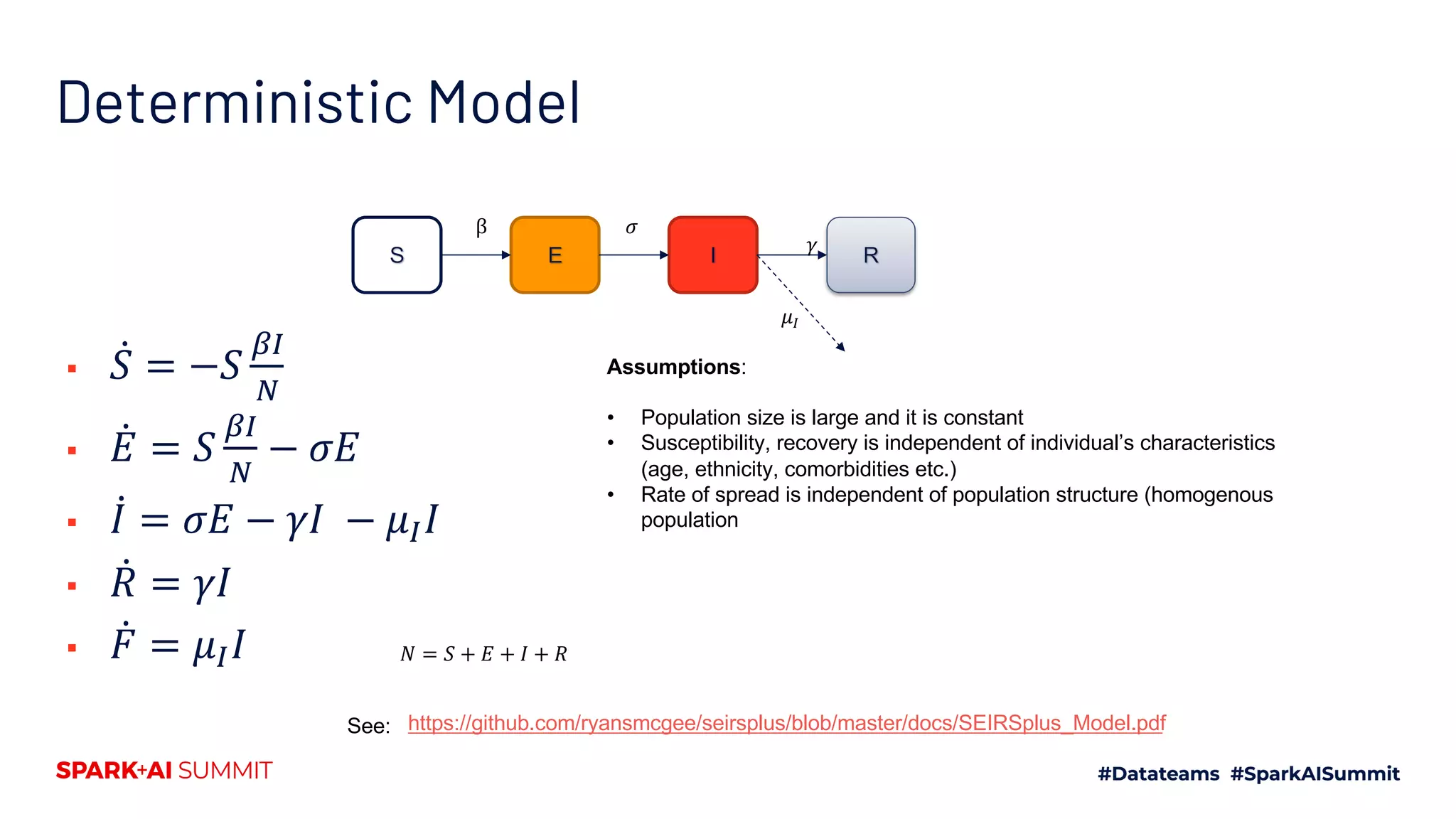
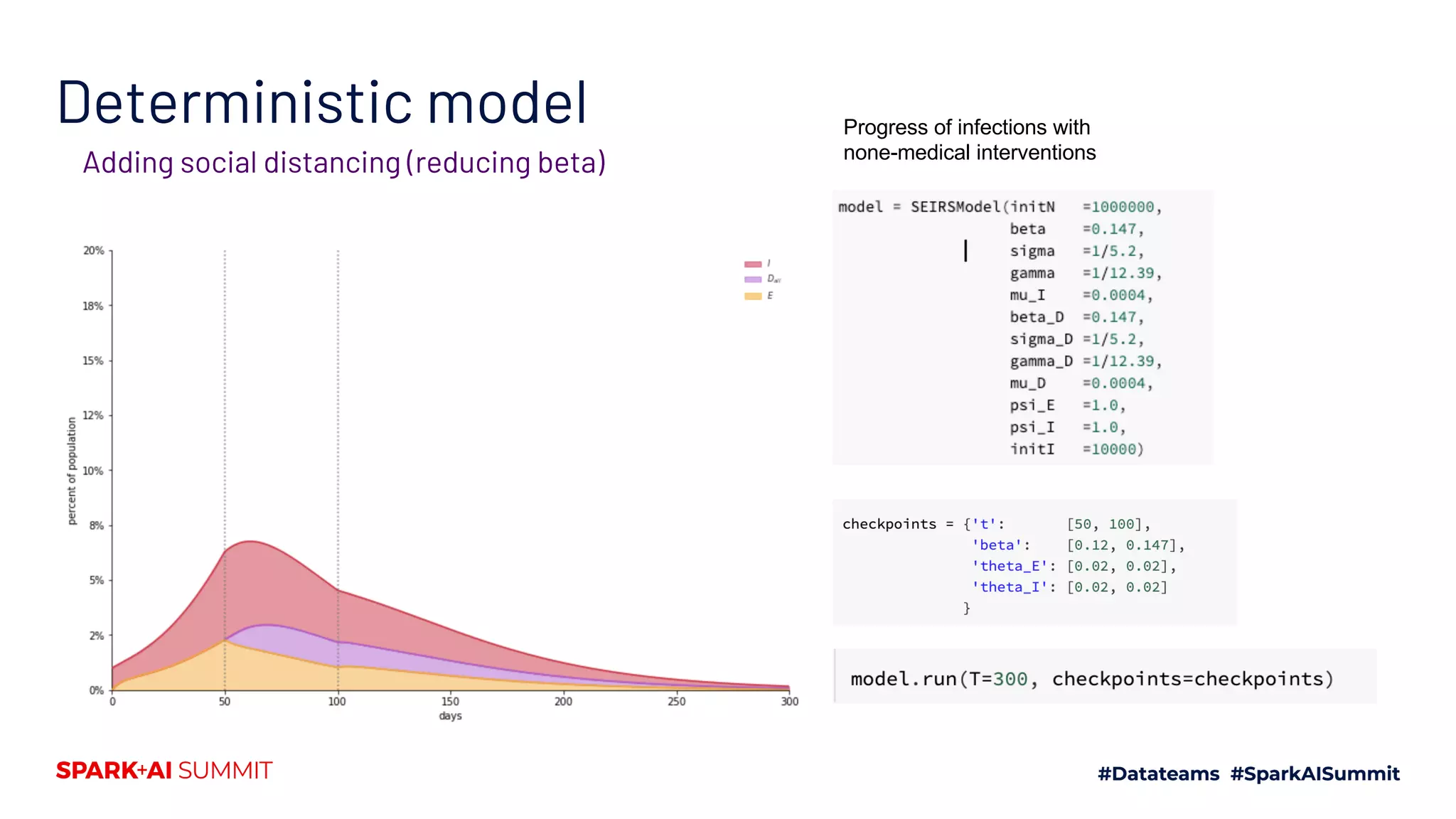
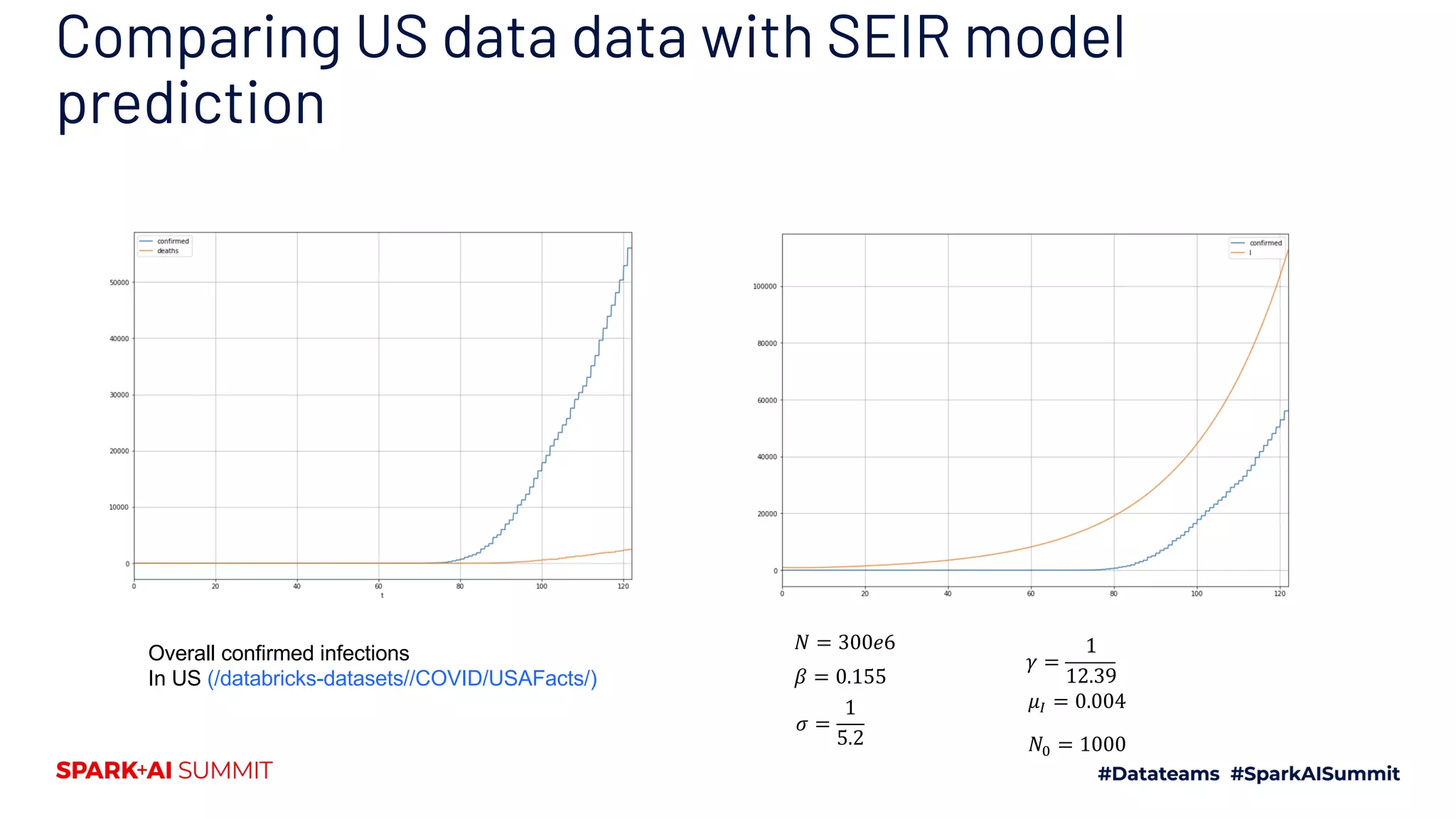
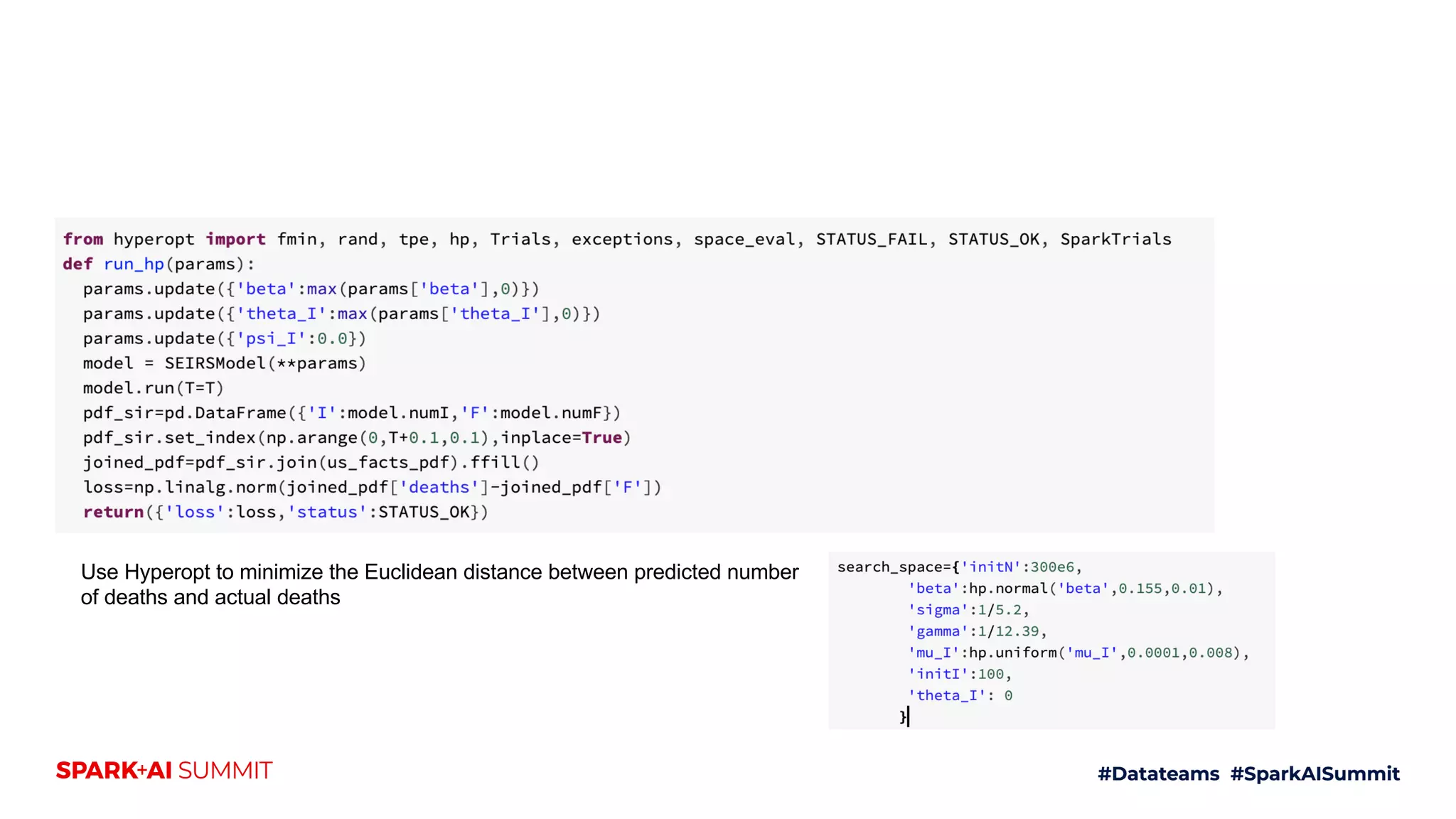
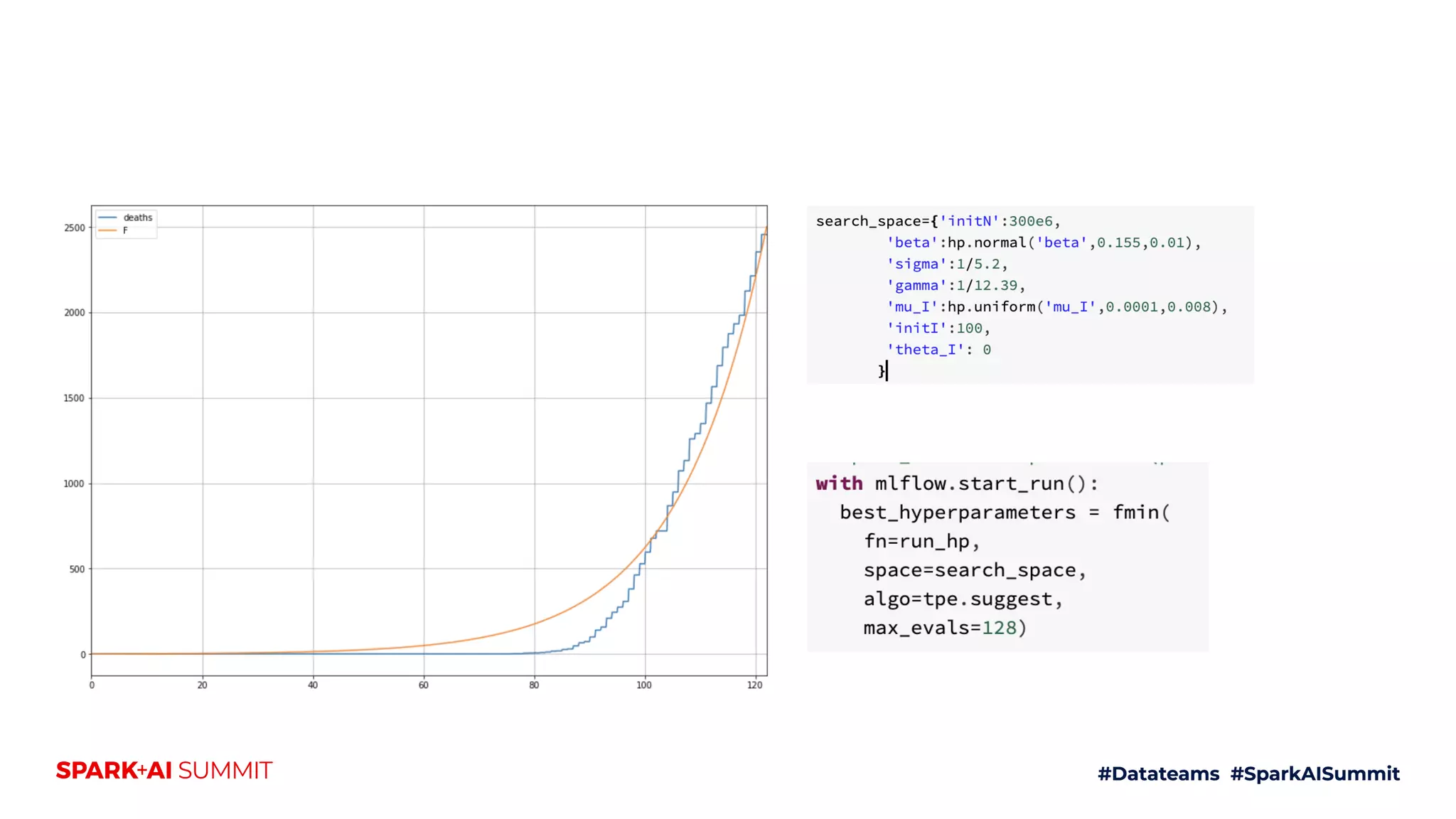
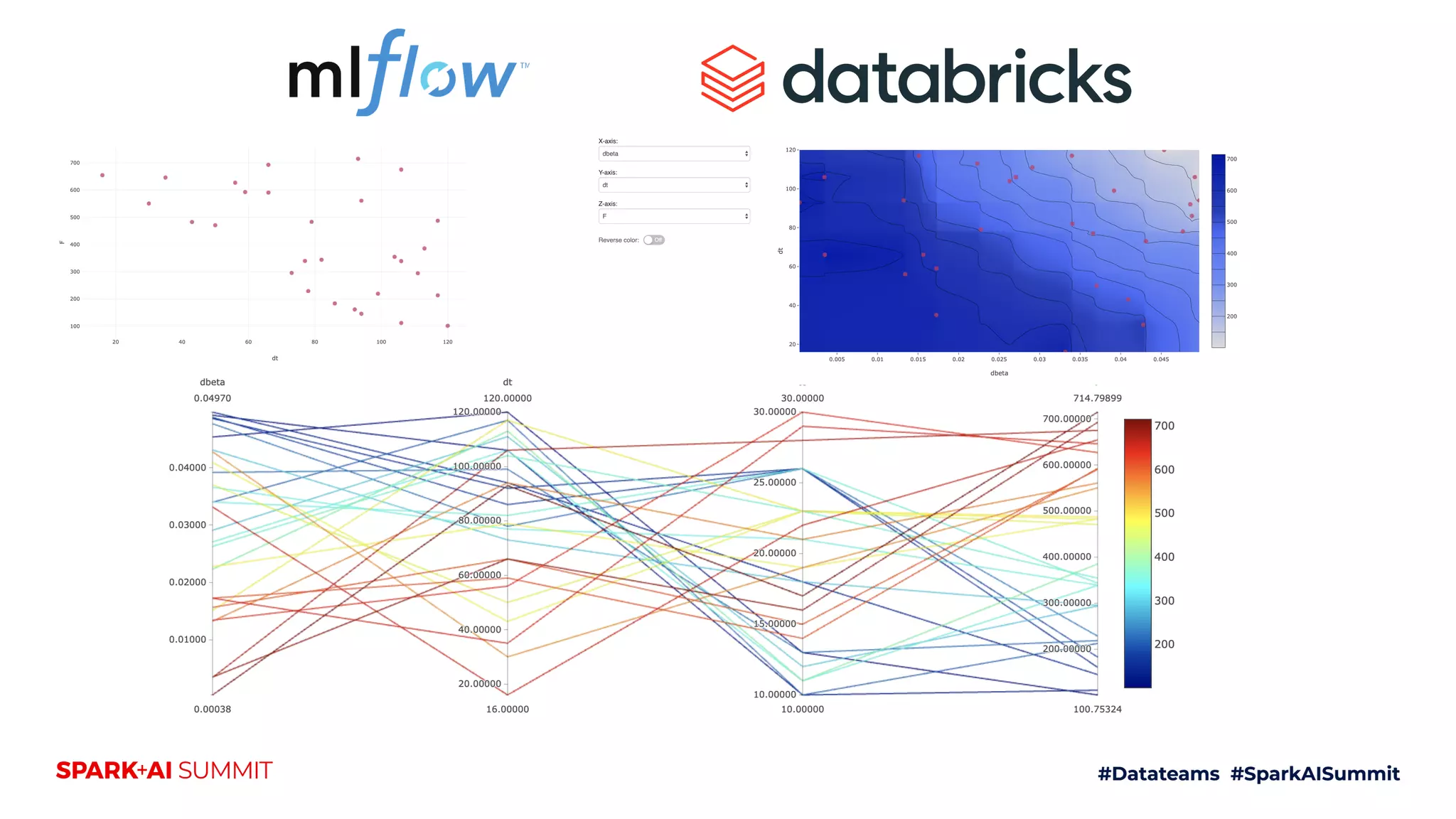
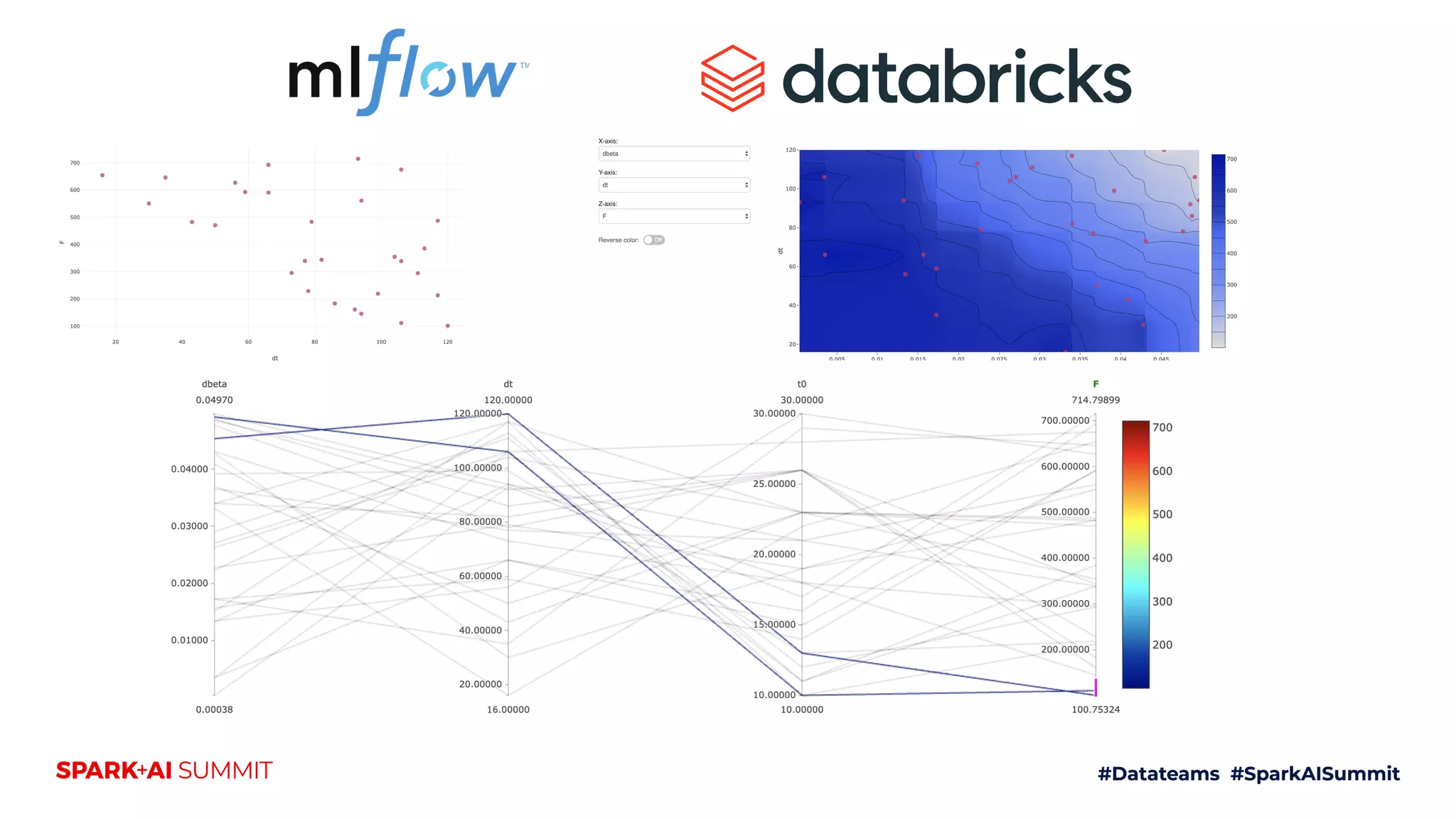
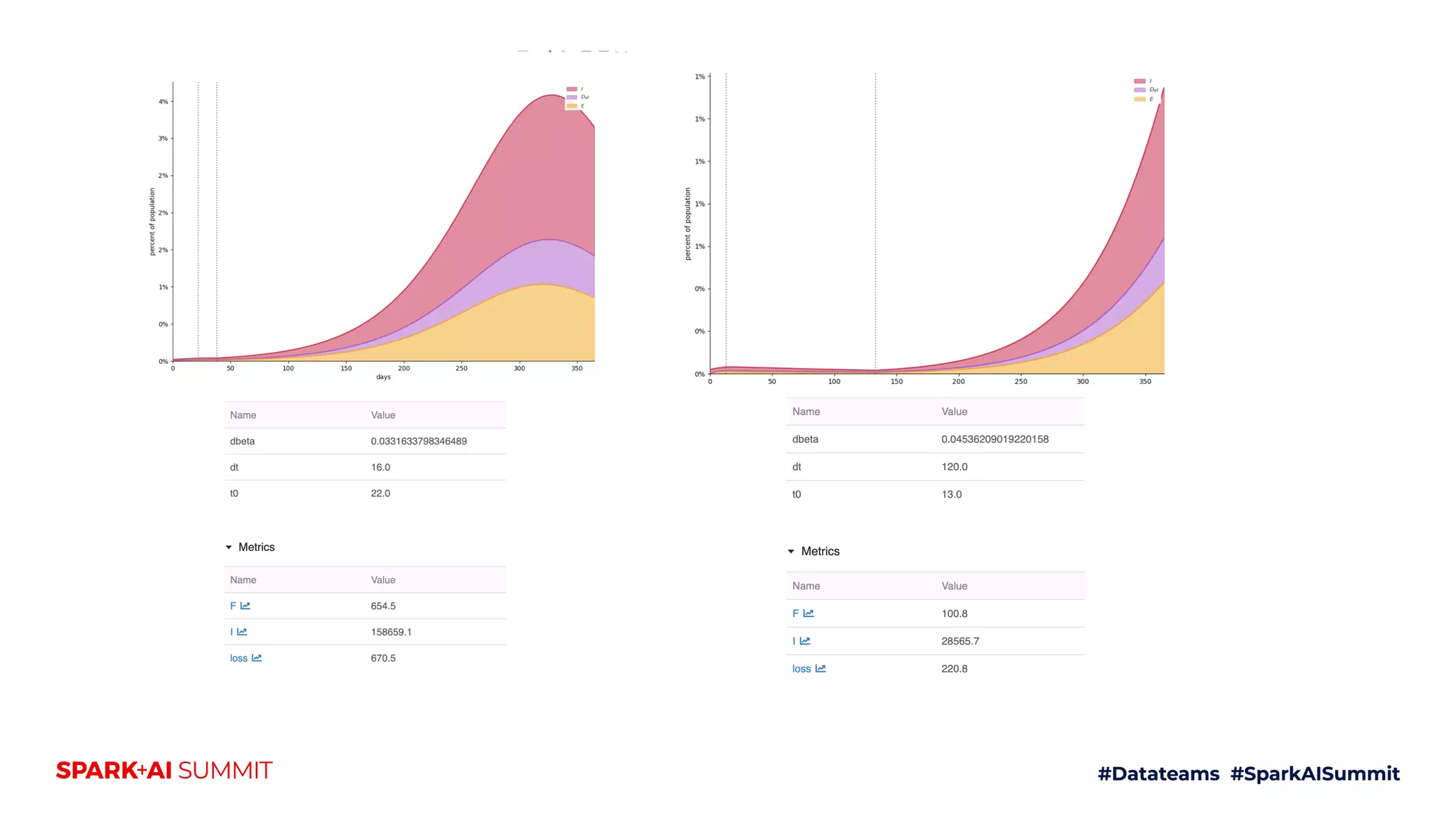
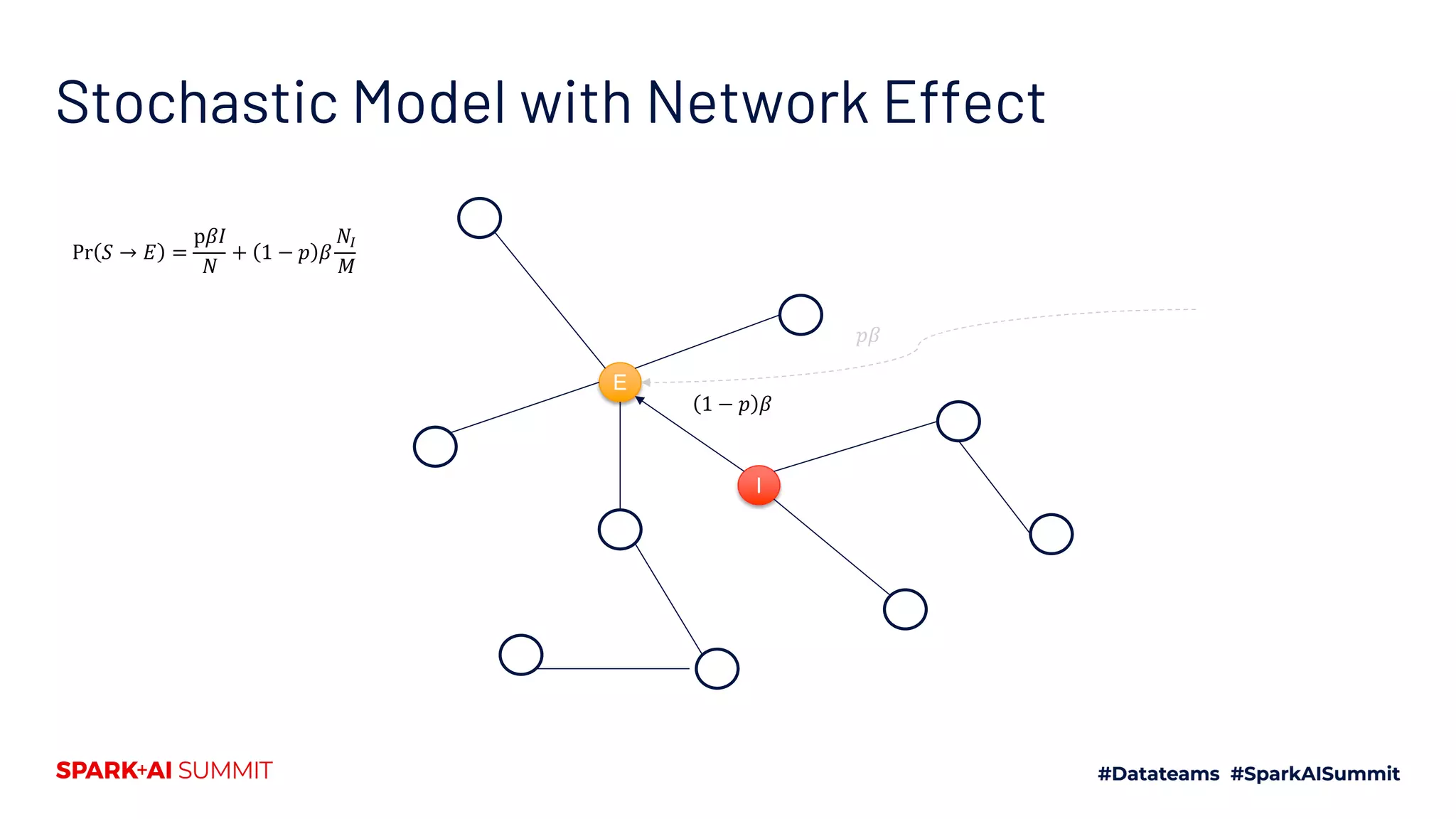
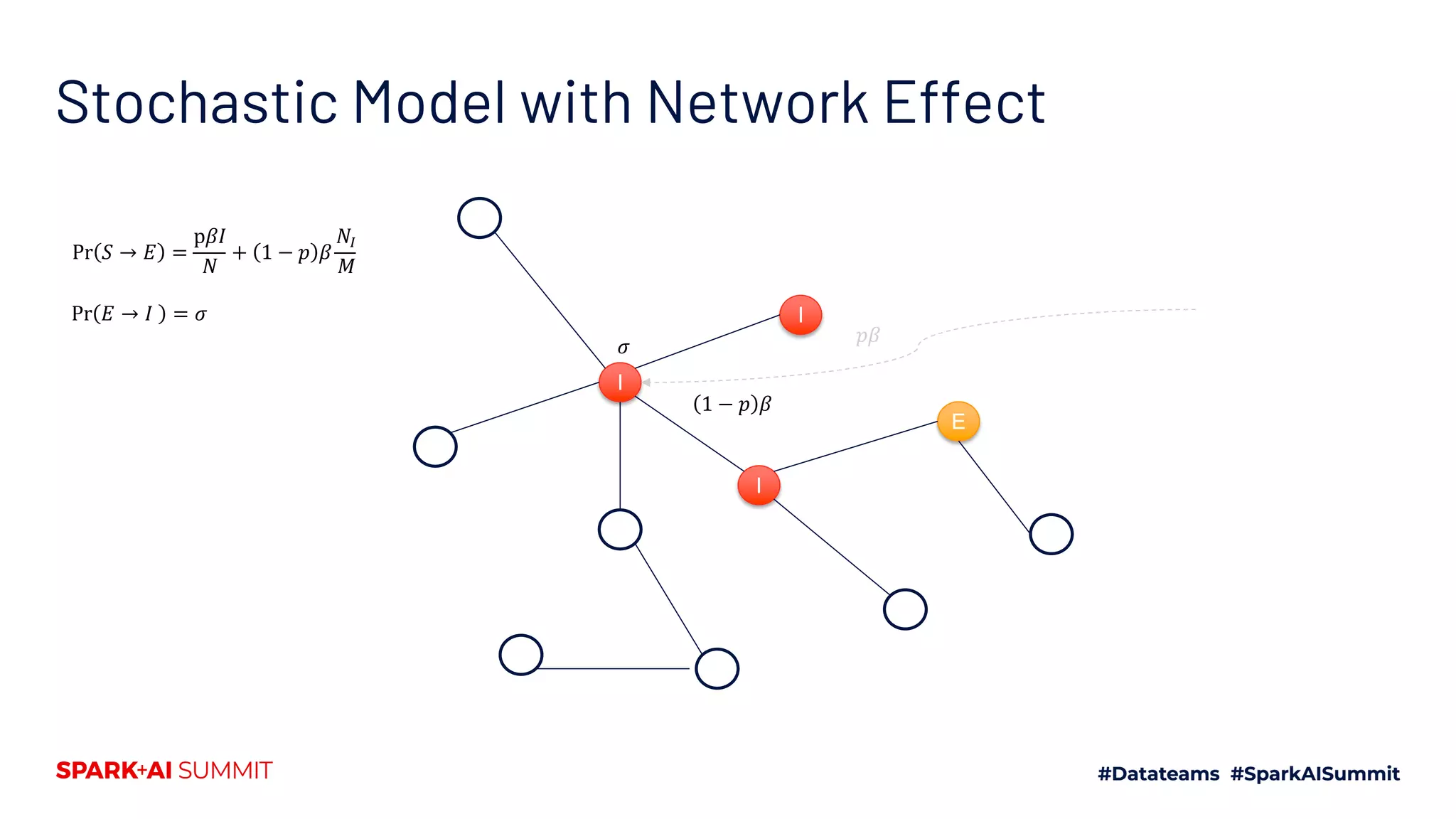
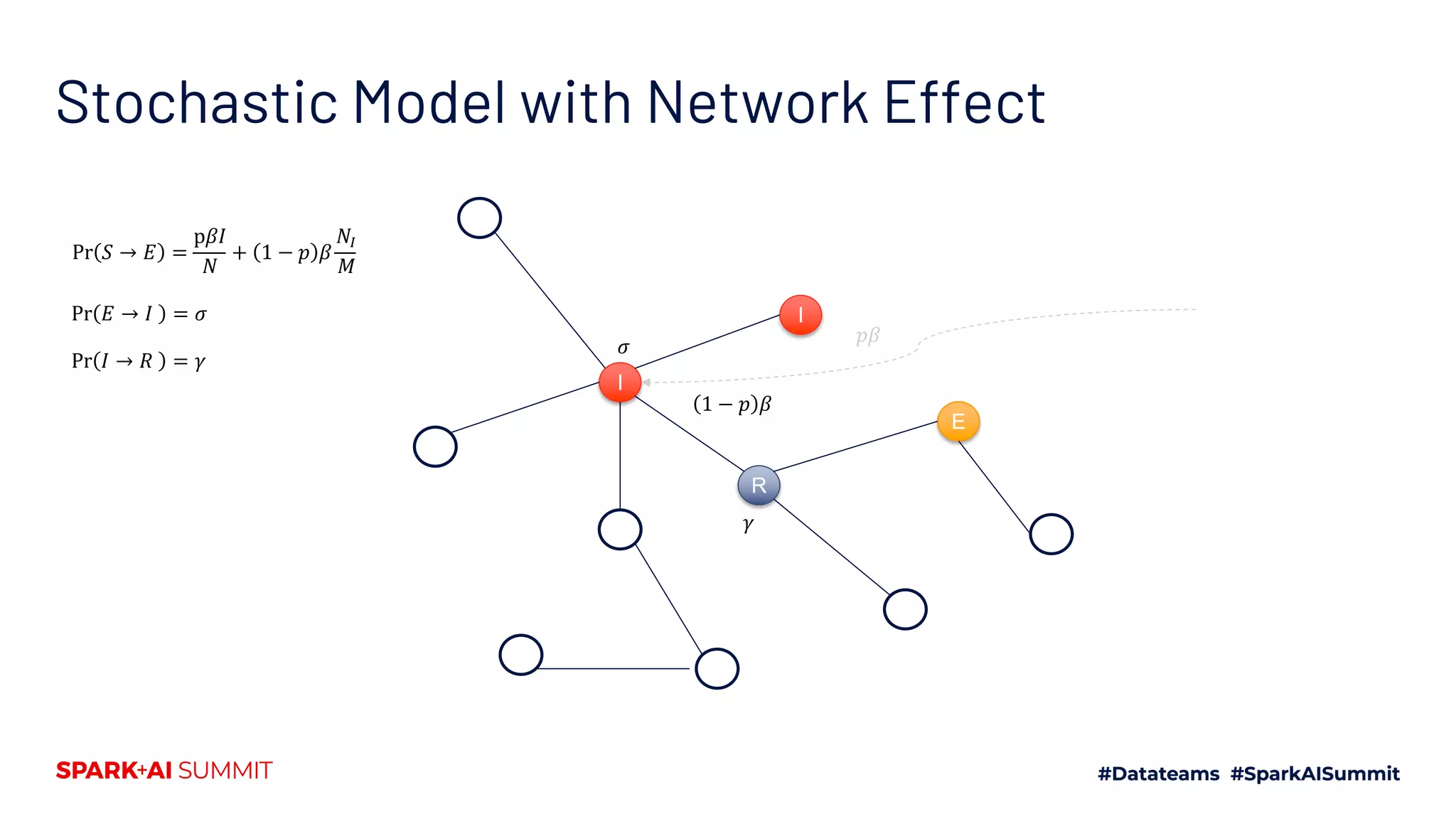
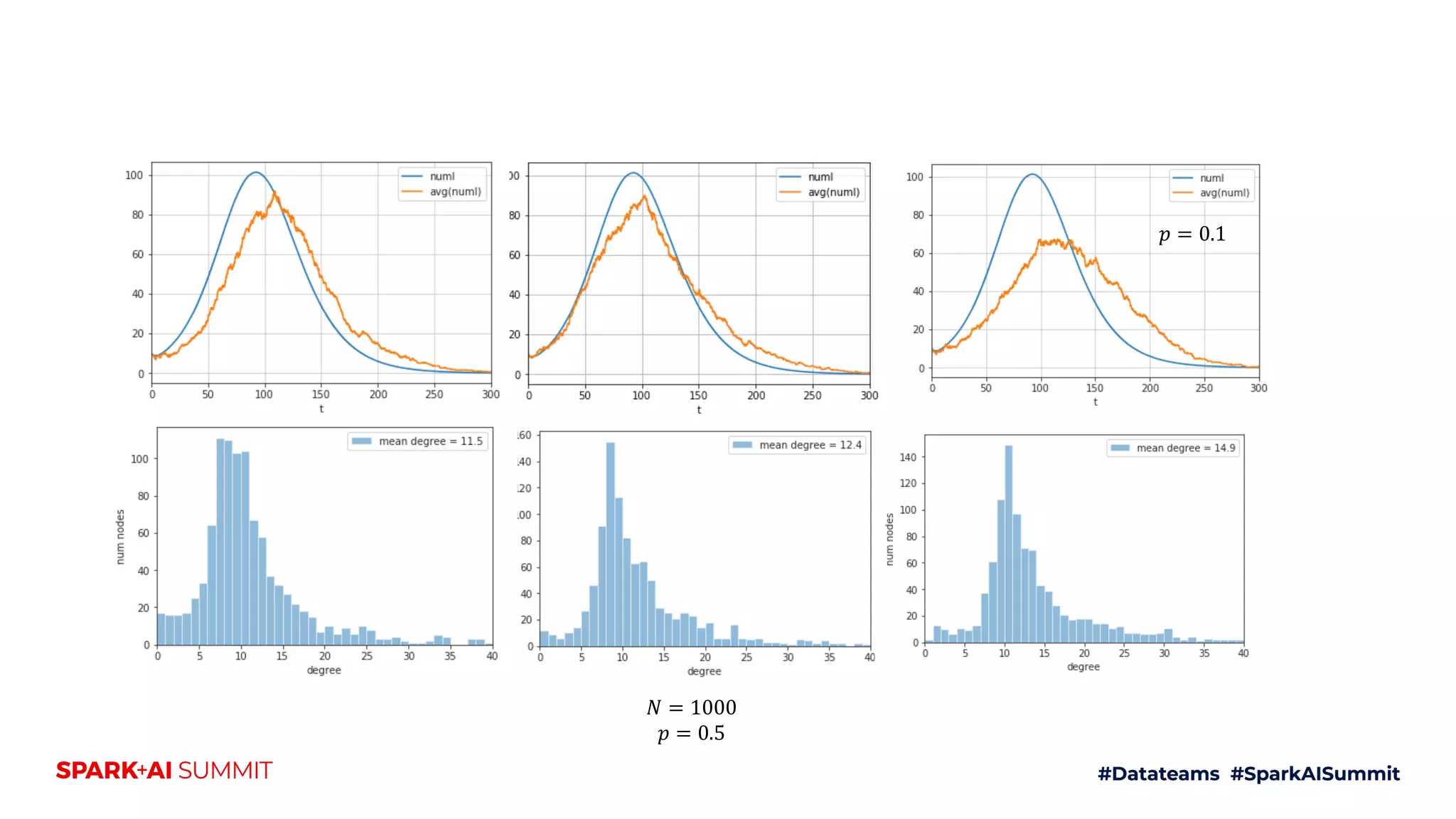
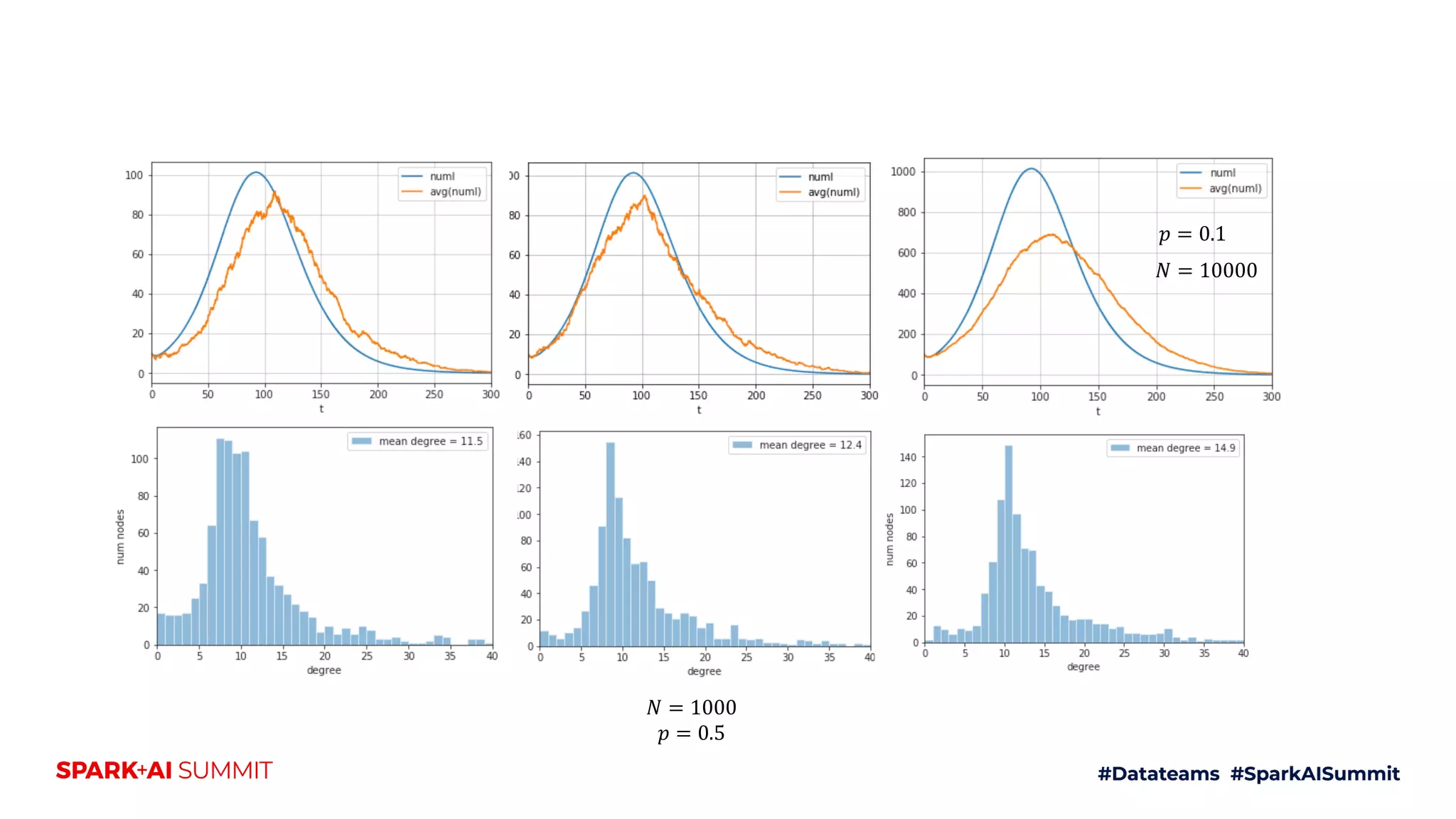
The document discusses the generalized SEIR model for infectious diseases, detailing its components and applications in estimating disease spread, forecasting, and informing policy decisions. It compares deterministic and stochastic models, highlights the use of the SEIRPlus package in simulations, and emphasizes the significance of data fitting and parameter estimation for effective modeling. Additionally, it outlines the impact of various interventions, such as social distancing, on disease dynamics using numerical solutions and optimization techniques.

2. Generalized SEIR Model
Amir Kermany, PhD.
Solutions Architect, Health and Life Sciences
Databricks

3. Agenda
▪ Introduction to SEIR model for infectious diseases
▪ Deterministic vs Stochastic models
▪ Predicting Spread of Disease using seirplus package
▪ Study the effect of different policies on progress of disease with
hyperopt and

4. Modeling infectious disease
Models are useful for
▪ Estimation: to estimate fundamental parameters (rate of spread, etc.)
▪ Forecasting: to project the spread of disease
▪ Inform policy: what are the impacts of different measures ?
▪ Behavior change: recommendations to the public (flattening the
curve)
”All models are wrong, but some are useful”

5. SIR Model
▪ SIR model is the simplest form of modeling the dynamics of infectious diseases in
a closed population
▪ It assumes that individuals in the population can take one of the three states of:
Susceptible, Infected or Removed (recover or die)
▪ The first example of such model is found in Kermack-McKendrick theory (1927-
1933) of infectious disease transmission
S(usceptible) I(nfected) R(emoved)

6. SEIR Model
▪ SEIR Model is a more general model that adds an extra state of Exposed
▪ This model is appropriate for diseases that have an incubation period (time between exposure and
infection)
S(usceptible), E(xposed) I(nfected) R(emoved)
𝛾𝜎β
𝛽 = rate of transmission per contact
𝜎= 1/𝜏 (𝜏 = incubation period)
𝛾 = recovery rate = 1/D (D = infectious period)𝜇!
𝜇!: fatality rate
𝜉= rate of re-infection

7. SEIR Model
▪ SEIR Model is a more general model that adds an extra state of Exposed
▪ This model is appropriate for diseases that have an incubation period (time between exposure and
infection)
S(usceptible), E(xposed) I(nfected) R(emoved)
𝛾𝜎β
𝛽 = rate of transmission per contact
𝜎= 1/𝜏 (𝜏 = incubation period)
𝛾 = recovery rate = 1/D (D = infectious period)𝜇!
𝜇!: fatality rate

8. Deterministic Model
▪ ̇𝑆 = −𝑆
!"
#
▪ ̇𝐸 = 𝑆
!"
#
− 𝜎𝐸
▪ ̇𝐼 = 𝜎𝐸 − 𝛾𝐼 − 𝜇" 𝐼
▪ ̇𝑅 = 𝛾𝐼
▪ ̇𝐹 = 𝜇" 𝐼
Assumptions:
• Population size is large and it is constant
• Susceptibility, recovery is independent of individual’s characteristics
(age, ethnicity, comorbidities etc.)
• Rate of spread is independent of population structure (homogenous
population
𝜎β
𝜇!
𝛾
𝑁 = 𝑆 + 𝐸 + 𝐼 + 𝑅
https://github.com/ryansmcgee/seirsplus/blob/master/docs/SEIRSplus_Model.pdfSee:

9. Deterministic Model with Testing
▪ ̇𝑆 = −𝑆
!"
#
− 𝑞𝛽$ 𝑆
$!
#
▪ ̇𝐸 = 𝑆
!"
#
+ 𝑆𝑞𝛽$
$!
#
− 𝜎𝐸 − 𝜃% 𝜓% 𝐸
▪ ̇𝐼 = 𝜎𝐸 − 𝛾𝐼 − 𝜇" 𝐼 − 𝜃" 𝜓" 𝐼
▪ ̇𝑅 = 𝛾𝐼 + 𝛾$ 𝐷"
▪ ̇𝐹 = 𝜇" 𝐼 + 𝜇$ 𝐷" ▪ ̇𝐷% = 𝜃% 𝜓% 𝐸 − 𝜎$ 𝐷%
▪ ̇𝐷" = 𝜃" 𝜓" 𝐼 + 𝜎$ 𝐷% − 𝛾$ 𝐷" − 𝜇$ 𝐷"
𝜎β
𝜇!
𝛾
𝜃" 𝜓" 𝜃! 𝜓! 𝛾#
𝜇#
𝜎#
https://github.com/ryansmcgee/seirsplus/blob/master/docs/SEIRSplus_Model.pdfSee:

10. Running Generalized SEIR model in python
▪ We use seriplus : https://github.com/ryansmcgee/seirsplus/ implementation of
SEIR with network effects
▪ Using this method you can specify different scenarios. For example quarantine,
case tracking and testing, and custom interaction networks
▪ We use hyperopt with spark trials to study the impact of each parameter on
fatality
▪ We also use mlflow experiments for tracking and explaining the effect of each
parameter

11. Deterministic model
Numeric solution to SEIR dynamical system
Progress of infections assuming no
intervention

12. Deterministic model
Adding social distancing (reducing beta)
Progress of infections with
none-medical interventions

13. Fitting data to model
▪ Using the deterministic model one can fit data to estimate parameters
in the system (e.g. 𝛽, 𝜎, 𝛾)
▪ This can be done using approximate solutions to the ODE
▪ In python for example you can use curve fitting tools such as
scipy.optimize.curve_fit
▪ A heuristic approach is to minimize distance between the precited
curve and data while searching over a grid of parameters
Estimation

14. Comparing US data data with SEIR model
prediction
𝑁 = 300𝑒6
𝛽 = 0.155
𝜎 =
1
5.2
𝛾 =
1
12.39
𝜇! = 0.004
𝑁$ = 1000
Overall confirmed infections
In US (/databricks-datasets//COVID/USAFacts/)

15. Use Hyperopt to minimize the Euclidean distance between predicted number
of deaths and actual deaths

17. What is the impact of different interventions?
▪ Impose social distancing (reduce beta) for a length of time dt, starting at a time t0
▪ Use hyperopt to minimize the cost loss=F+x*dt, where x is a cost per day of lockdown and F is the total
fatalities
Inform policy

21. Stochastic vs Deterministic Simulation
Determinist model assumptions:
▪ Population size is large and is constant
▪ Susceptibility, recovery is independent of individual’s characteristics (age,
ethnicity, comorbidities etc)
• Rate of spread is independent of population structure and variation in social
interactions

22. Stochastic vs Deterministic Simulation

23. Stochastic vs Deterministic Simulation
Determinist model assumptions:
▪ Population size is large and is constant
▪ Susceptibility, recovery is independent of individual’s characteristics
(age, ethnicity, comorbidities etc)
• Rate of spread is independent of population structure and variation in social
interactions

25. Stochastic vs Deterministic Simulation
Determinist model assumptions:
▪ Population size is large and is constant
▪ Susceptibility, recovery is independent of individual’s characteristics
(age, ethnicity, comorbidities etc)
• Rate of spread is independent of population structure and variation in social
interactions

26. Stochastic Model with Network Effect

27. Stochastic Model with Network Effect
I

28. Stochastic Model with Network Effect
E
I
𝑝𝛽
Pr 𝑆 → 𝐸 =
p𝛽𝐼
𝑁

29. Stochastic Model with Network Effect
E
I
1 − 𝑝 𝛽
𝑝𝛽
Pr 𝑆 → 𝐸 =
p𝛽𝐼
𝑁
+ 1 − 𝑝 𝛽
𝑁!
𝑀

30. Stochastic Model with Network Effect
I
I
𝜎
1 − 𝑝 𝛽
𝑝𝛽
Pr 𝑆 → 𝐸 =
p𝛽𝐼
𝑁
+ 1 − 𝑝 𝛽
𝑁!
𝑀
Pr 𝐸 → 𝐼 = 𝜎

31. Stochastic Model with Network Effect
I
E
I
𝜎
1 − 𝑝 𝛽
𝑝𝛽
Pr 𝑆 → 𝐸 =
p𝛽𝐼
𝑁
+ 1 − 𝑝 𝛽
𝑁!
𝑀
Pr 𝐸 → 𝐼 = 𝜎

32. Stochastic Model with Network Effect
I
I
I
E
𝜎
1 − 𝑝 𝛽
𝑝𝛽
Pr 𝑆 → 𝐸 =
p𝛽𝐼
𝑁
+ 1 − 𝑝 𝛽
𝑁!
𝑀
Pr 𝐸 → 𝐼 = 𝜎

33. Stochastic Model with Network Effect
I
I
R
E
𝜎
1 − 𝑝 𝛽
𝛾
𝑝𝛽
Pr 𝑆 → 𝐸 =
p𝛽𝐼
𝑁
+ 1 − 𝑝 𝛽
𝑁!
𝑀
Pr 𝐸 → 𝐼 = 𝜎
Pr 𝐼 → 𝑅 = 𝛾

34. Stochastic Model with Network Effect
I
I
R
E
𝜎
1 − 𝑝 𝛽
𝛾
𝑝𝛽
Pr 𝑆 → 𝐸 =
p𝛽𝐼
𝑁
+ 1 − 𝑝 𝛽
𝑁!
𝑀
Pr 𝐸 → 𝐼 = 𝜎
Pr 𝐼 → 𝑅 = 𝛾

35. Stochastic model with network interactions

36. Parallel simulations with

37. 𝑁 = 1000
𝑝 = 0.5

38. 𝑁 = 1000
𝑝 = 0.5
𝑝 = 0.1

39. 𝑁 = 1000
𝑝 = 0.5
𝑝 = 0.1𝑝 = 0.1
𝑁 = 10000

40. Conclusions
▪ Use Hyperopt+ in databricks ML Runtime to track different
experiments and easily visualize the effect of different parameters on
the spread of disease
▪ Use to parallelize different runs of the stochastic model
▪ Network structure has a significant impact on the spread of the
disease even in large populations

41. Questions