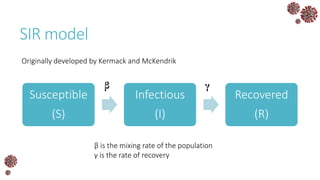
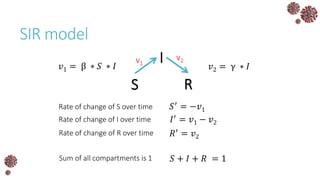
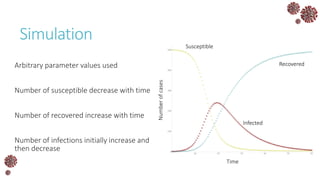
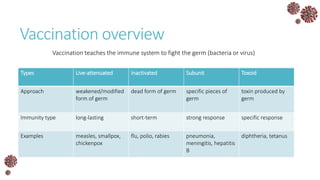
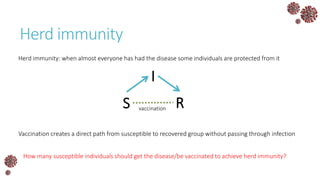
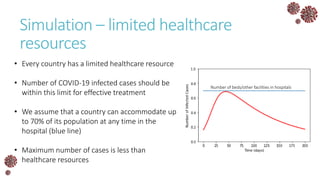
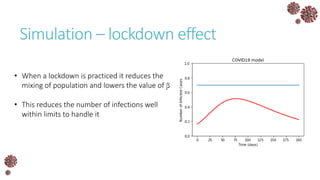
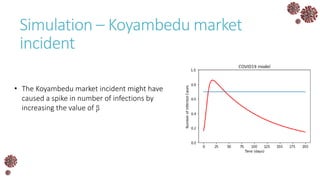
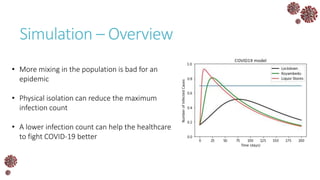
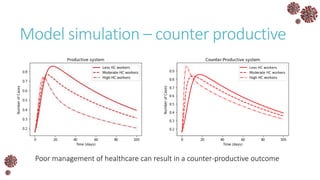
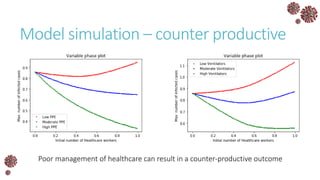
The document discusses the mathematical modeling of epidemics, with a focus on COVID-19, explaining historical modeling efforts and key concepts like the SIR model. It highlights the importance of herd immunity, vaccination strategies, and the impact of healthcare resource limitations on disease spread. The document also explores modifications of models to account for factors like healthcare workers and the effects of lockdowns and social behaviors on infection rates.

1. Mathematically
modelling the spread of
COVID-19
Thawfeek Mohamed Varusai
Scientific Data Analyst, EMBL-EBI, Cambridge, UK

2. History of modelling epidemics
Started as early as the 15th century.
First prominent modelling effort was done in the 16th century by Daniel Bernoulli to
understand small pox vaccination
Other early efforts include the spatial and temporal study of cholera spread in London
by John Snow in the mid 17th century

3. Compartmental modelling
Most commonly used approach in epidemiology.
In the early 20th century it was believed that so long as mosquitoes were present in a population
malaria cannot be eliminated.
Dr Ross won the Nobel prize in 1902 for proving that malaria can be overcome by merely reducing
the mosquitoes population below a critical level.
He used a compartmental modelling approach to study the spread of malaria to estimate precise
numbers.
The concept of ‘basic reproduction number’ (R0) was born here.

4. Stochastic modelling
Used when there is incomplete mixing in a population –small population or people
with restriction contacts
In the initial phase of the epidemic, there are very few infected individuals who
have limited contacts
Under these circumstances, stochastic modelling is used to predict the spread

5. SIR model
Susceptible
(S)
Infectious
(I)
Recovered
(R)
Originally developed by Kermack and McKendrik
β γ
β is the mixing rate of the population
γ is the rate of recovery

6. SIR model
S
I
R
v1
v2
𝑆′
= −𝑣1
𝐼′ = 𝑣1 − 𝑣2
𝑅′ = 𝑣2
Rate of change of S over time
Rate of change of I over time
Rate of change of R over time
𝑆 + 𝐼 + 𝑅 = 1Sum of all compartments is 1
𝑣1 = β ∗ 𝑆 ∗ 𝐼 𝑣2 = γ ∗ 𝐼

7. SIR model – assumptions
Closed system: ignoring birth/death or immigration, etc.
Reinfection is not considered
All individuals in the population have the same chances of getting infected
The population is considered to be well mixed

8. Simulation
Arbitrary parameter values used
Number of susceptible decrease with time
Number of recovered increase with time
Number of infections initially increase and
then decrease
Susceptible
Recovered
Infected
TimeNumberofcases

9. SIR model – R0
𝐼′
= 𝑣1 − 𝑣2
Basic reproductive number (R0) is defined as the average number of people infected by an infected individual
= β ∗ 𝑆 ∗ 𝐼 − γ ∗ 𝐼
= (β ∗ 𝑆 − γ) ∗ 𝐼
When everyone in the population is susceptible: S = 1 (since I and R are 0 in S + I + R = 1)
= (β − γ) ∗ 𝐼𝐼′ = 𝑣1 − 𝑣2

10. SIR model – R0
= (β − γ) ∗ 𝐼𝐼′ = 𝑣1 − 𝑣2
For I’ to increase the right hand side must be positive:
β − γ > 0
β > γ
β
γ
> 1
𝑅0 > 1
For I’ to decrease the right hand side must be negative:
β − γ < 0
β < γ
β
γ
< 1
𝑅0 < 1
A disease will not spread if R0<1 and an epidemic will occur if R0>1
Rate of change of infections
𝑹 𝟎 =
𝜷
𝜸
For measles: R0 is about 16
For COVID-19: R0 is estimated to be around 3.5

11. Vaccination overview
Vaccination teaches the immune system to fight the germ (bacteria or virus)
Types Live-attenuated Inactivated Subunit Toxoid
Approach weakened/modified
form of germ
dead form of germ specific pieces of
germ
toxin produced by
germ
Immunity type long-lasting short-term strong response specific response
Examples measles, smallpox,
chickenpox
flu, polio, rabies pneumonia,
meningitis, hepatitis
B
diphtheria, tetanus

12. Herd immunity
Vaccination creates a direct path from susceptible to recovered group without passing through infection
How many susceptible individuals should get the disease/be vaccinated to achieve herd immunity?
S
I
Rvaccination
Herd immunity: when almost everyone has had the disease some individuals are protected from it

13. SIR model – herd immunity
(β ∗ 𝑆 − γ) ∗ 𝐼𝐼′
=Rate of change of infections
For infection to stop spreading:
𝐼′ = 0
β ∗ 𝑆 − γ = 0
since S + I + R = 1β ∗ (1 − (𝐼 + 𝑅)) − γ = 0
let (I + R) = ρβ ∗ (1 − ρ) − γ = 0
rearrangingρ = 1 −
γ
β
since 𝑅0 =
β
γρ = 𝟏 −
𝟏
𝑹 𝟎
Population that needs to be immune
For measles: ρ is close to 0.95
For COVID-19: ρ is estimated to be close to 0.70

14. SARS-CoV2
COVID-19 is a disease spread by a virus in the beta family of corona viruses
There have been other epidemics with the same family of virus before this – SARS in
2002, MERS in 2013 and now its COVID-19
COVID-19 virus is very similar to the SARS virus from 2002 and is also known as SARS-
CoV2
The primary infection site is the respiratory system through which the virus can enter
host cells and later spread to other organs

15. SIR model of SARS-CoV2
S
I
R
v1
v2
𝑣1 = β ∗ 𝑆 ∗ 𝐼 𝑣2 = γ ∗ 𝐼
𝑆′
= −𝑣1
𝐼′ = 𝑣1 − 𝑣2
𝑅′ = 𝑣2
𝑆 + 𝐼 + 𝑅 = 1
We don’t consider patient death in this basic model

16. Interpreting parameters
β is the mixing rate of the population (depends on awareness/laws)
γ is the rate of recovery (depends on medical facilities and medicines)
R0 for COVID-19 seems to between 3 and 4 (on average 3.5 people are infected by an
infected individual)
ρ for COVID-19 seems to be close to 0.7 (70% of the population should be
infected/vaccinated before herd immunity)

17. Simulation – limited healthcare
resources
• Every country has a limited healthcare resource
• Number of COVID-19 infected cases should be
within this limit for effective treatment
• We assume that a country can accommodate up
to 70% of its population at any time in the
hospital (blue line)
• Maximum number of cases is less than
healthcare resources
Number of beds/other facilities in hospitals

18. Simulation – lockdown effect
• When a lockdown is practiced it reduces the
mixing of population and lowers the value of β
• This reduces the number of infections well
within limits to handle it

19. Simulation – Koyambedu market
incident
• The Koyambedu market incident might have
caused a spike in number of infections by
increasing the value of β

20. Simulation – liquor stores opening effect
• Opening liquor stores can greatly increase the
value of β and result in higher infections

21. Simulation – Overview
• More mixing in the population is bad for an
epidemic
• Physical isolation can reduce the maximum
infection count
• A lower infection count can help the healthcare
to fight COVID-19 better

22. Parameter estimation from real data
For our model we used hypothetical values for parameters
In the real world model parameters are estimated using observed data
The aim is to match the predicted and observed data points as close as possible

23. Modifications of SIR model
Detailed models can predict real-life situations better
Special cases for vector-based endemic diseases
Different approach for population heterogeneity
Different approach for age-based vulnerability

24. SIR model with doctors/nurses/cleaners
H is a new compartment including
doctors/nurses/cleaners and all other staff who work in
the frontline of treating COVID-19
H has two roles in treating an epidemic:
1. H can treat patients and cure the disease
2. If not protected with PPE, H can also become a
patient
S
I
R
H 1
2

25. SIR model with doctors/nurses/cleaners
S
I
R
H
v1
v2
v3
v4
𝑣1 = β ∗ 𝑆 ∗ 𝐼
𝑣2 = γ1 ∗ 𝐼
𝑣3 = (1 − 𝑃𝑃𝐸) ∗ 𝐻 ∗ 𝐼
𝑣4 = (γ2 ∗ 𝑉𝑒𝑛𝑡) ∗ 𝐻 ∗ 𝐼
𝑆′ = −𝑣1
𝐼′ = 𝑣1 − 𝑣2 +𝑣3 − 𝑣4
𝑅′
= 𝑣2 + 𝑣4
𝑆 + 𝐼 + 𝑅 + 𝐻 = 1
𝐻′
= −𝑣3

26. SIR model with doctors/nurses/cleaners
‘H’ (green) decreases in the model because healthcare workers are infected due
to the lack of PPE
S
I
R
H

27. Interpreting parameters
β : population mixing rate
γ1 : natural recovery rate
PPE : PPE fraction available
(1-PPE) : contact rate of healthcare workers with patients
γ2 : recovery rate with treatment
Vent : ventilator/other equipment fraction available

28. Model parameters – poor management
Inadequate PPE supplies
Low PPE value in model
Insufficient ventilators and other medical equipment
Low Vent value in model

29. Model simulation – counter productive
Poor management of healthcare can result in a counter-productive outcome

30. Model simulation – counter productive
Poor management of healthcare can result in a counter-productive outcome

31. SIR model with doctors/nurses/cleaners
Interested audience can read more about this model creation and simulation in my
blog (links below).
1. https://medium.com/modelling-covid19-pandemic/role-of-healthcare-workers-in-
the-sir-epidemiological-model-
6e1ec046797d?source=friends_link&sk=a07c1bf6c830e17151fc97392d3c8982
2. https://medium.com/modelling-covid19-pandemic/a-surge-of-healthcare-workers-
can-be-bad-news-for-covid19-pandemic-
81ca3328eff2?source=friends_link&sk=5a619f9894f00950caa2596d523c6ef9

32. Take home messages
SIR model is a simple model that can give valuable insights into the spread of an
epidemic
Every epidemic is different and the model has to be modified to simulate real world
cases
Reducing the mixing rate of population and providing adequate healthcare support
seems to be the way to handle COVID-19 pandemic

33. Other DIY modelling
How will variable immunity impact COVID-19 spread?
How will opening public transport affect the disease spread?
How will migrant workers change the spread?