Download as PDF, PPTX
From unconventional to extreme to functional materials.
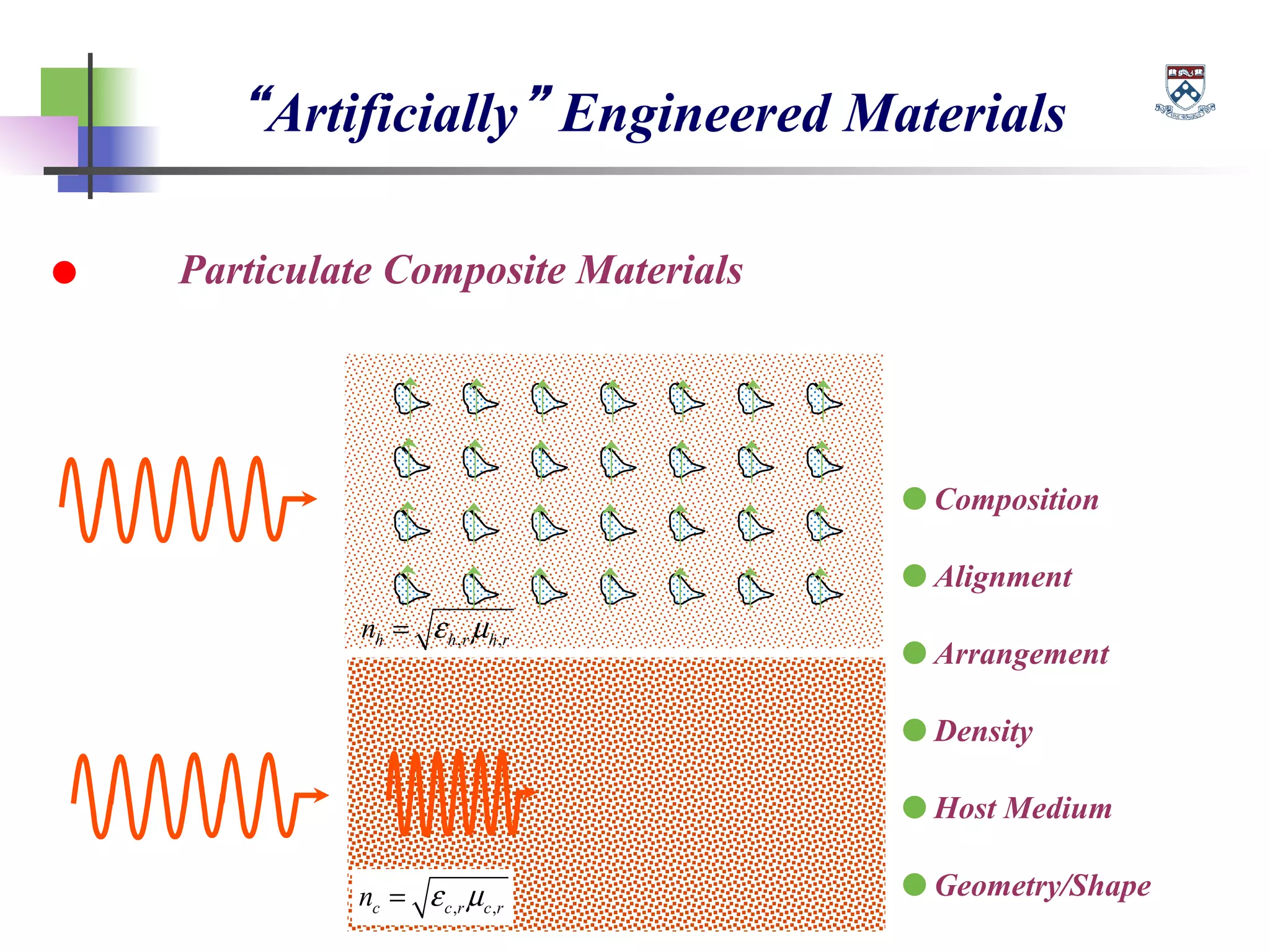
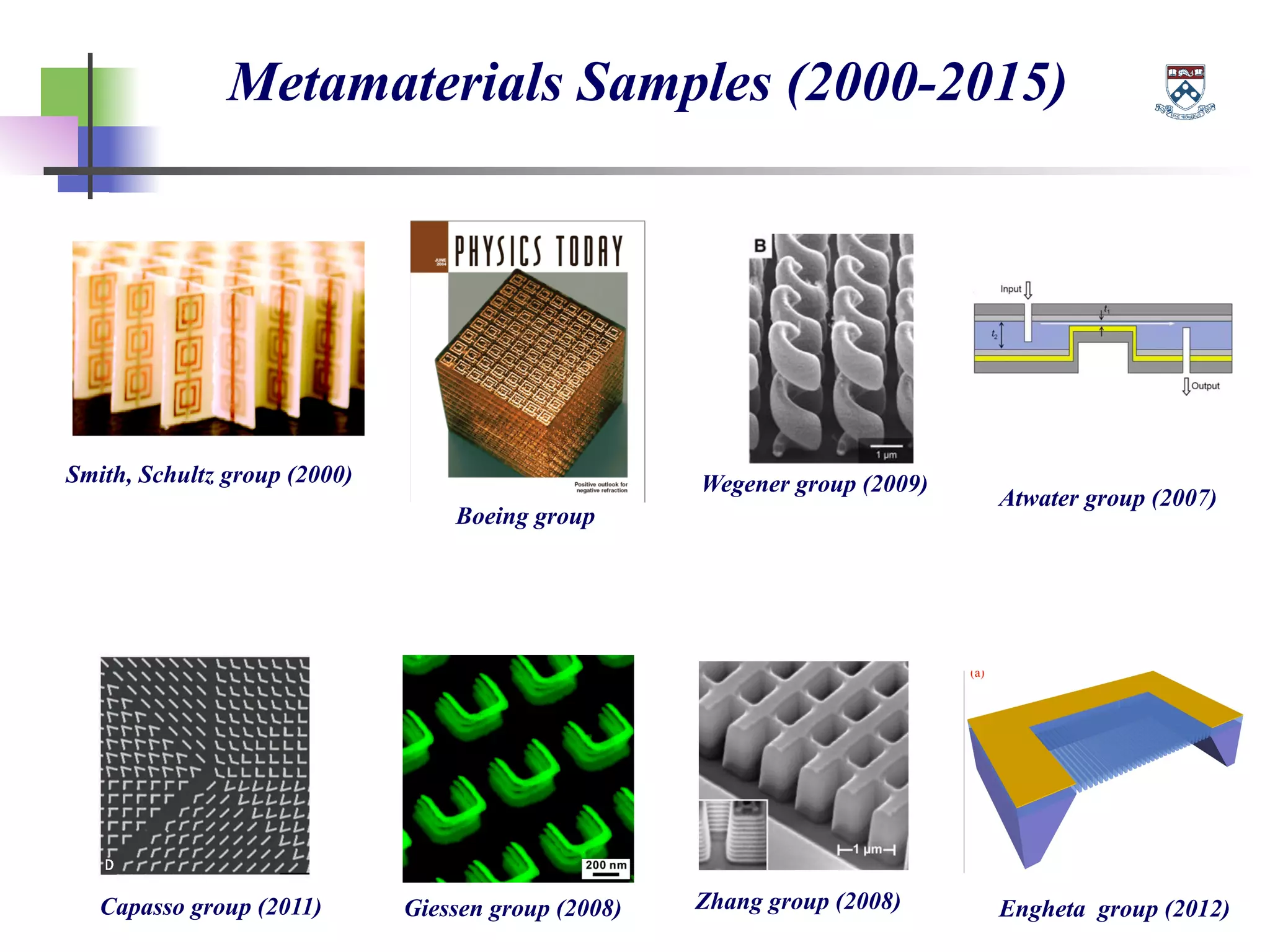
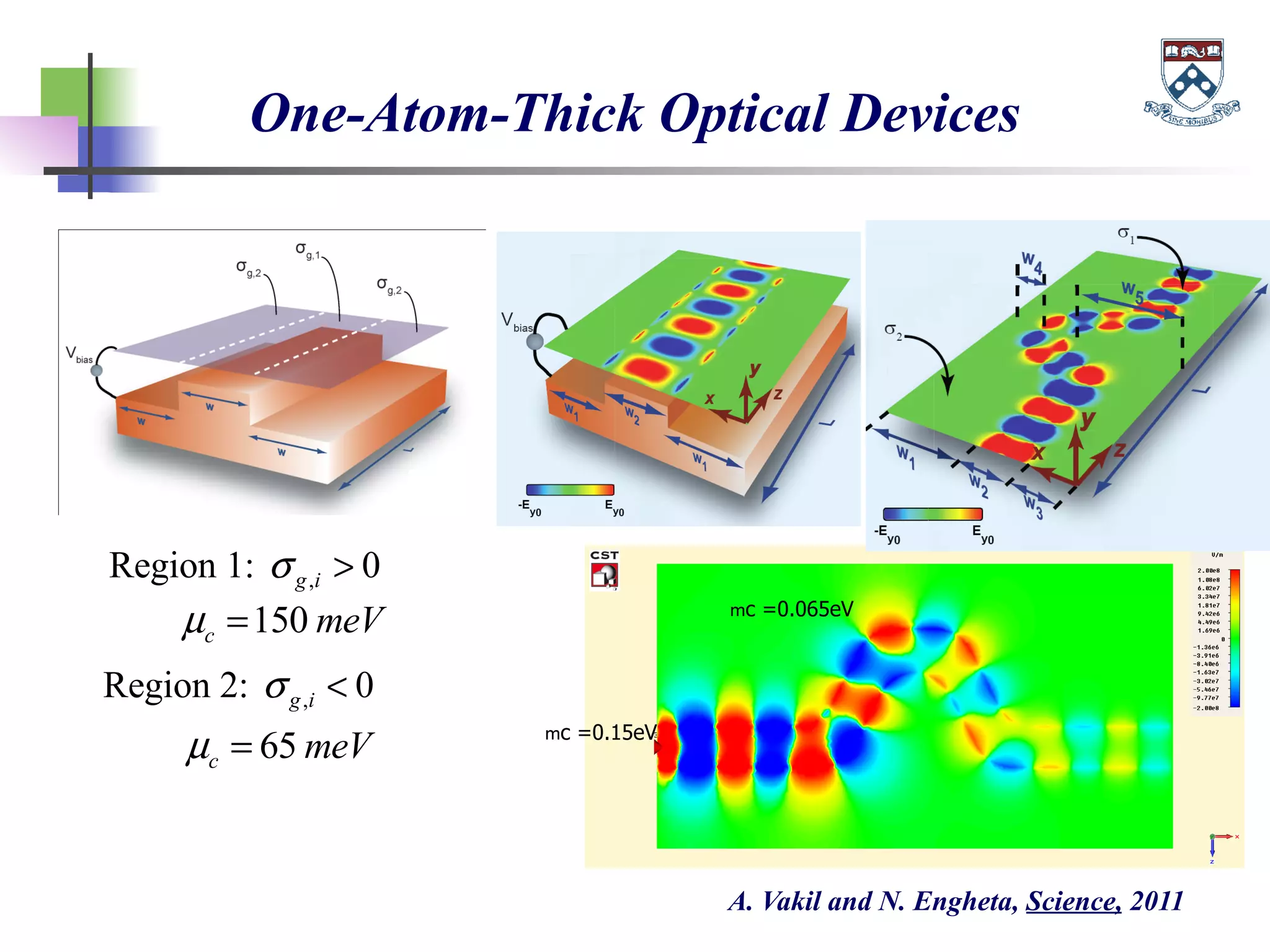
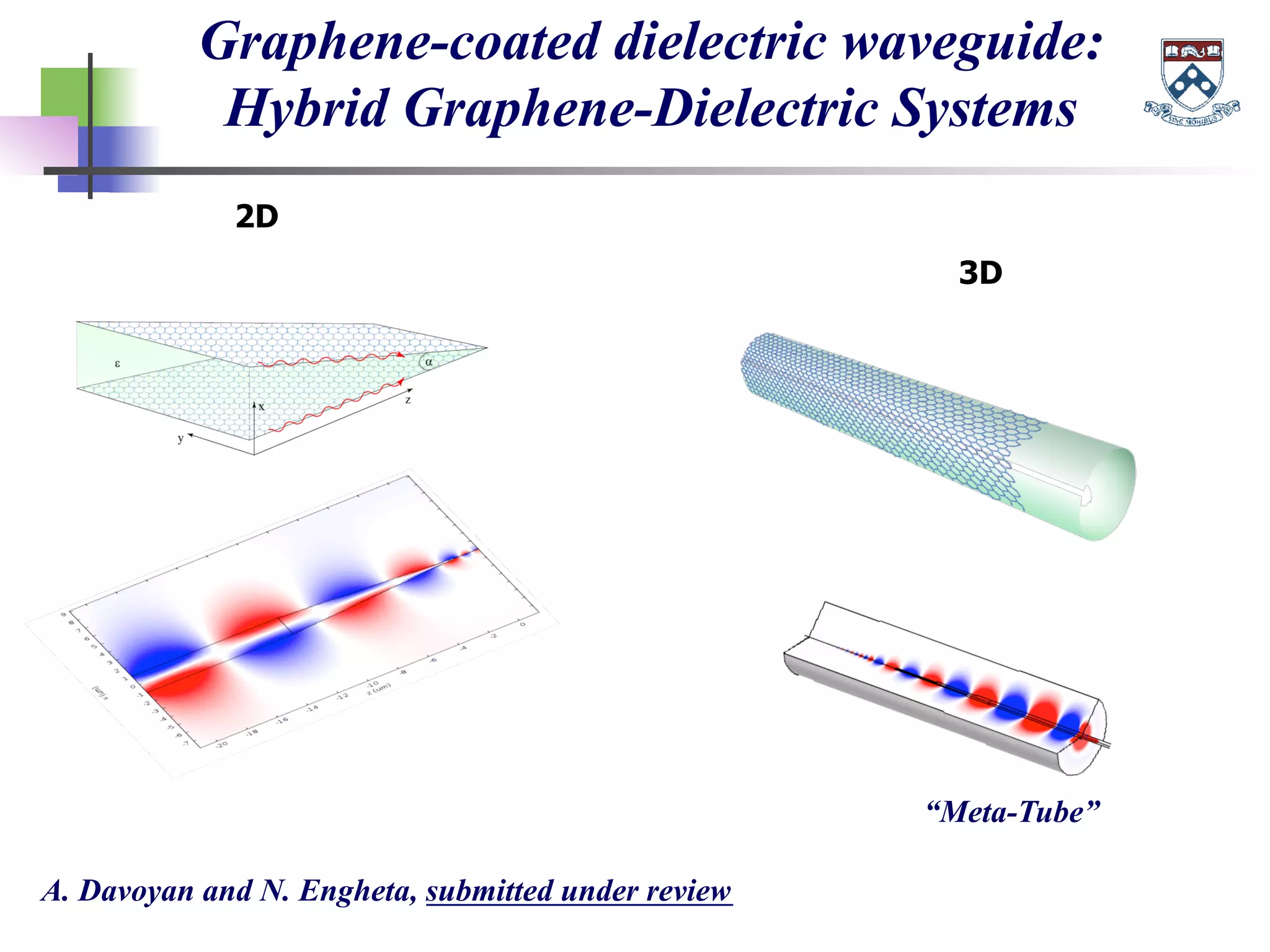
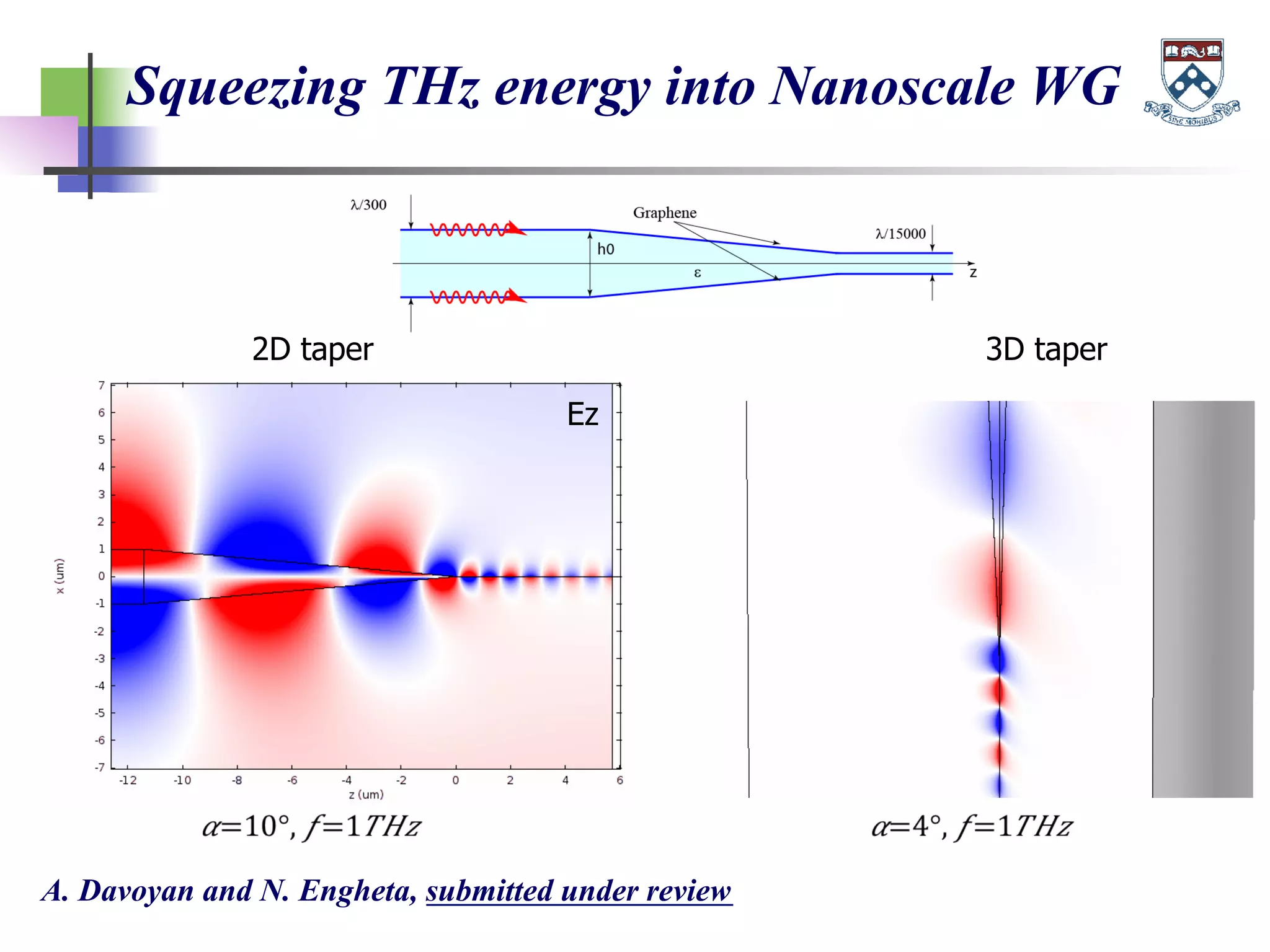
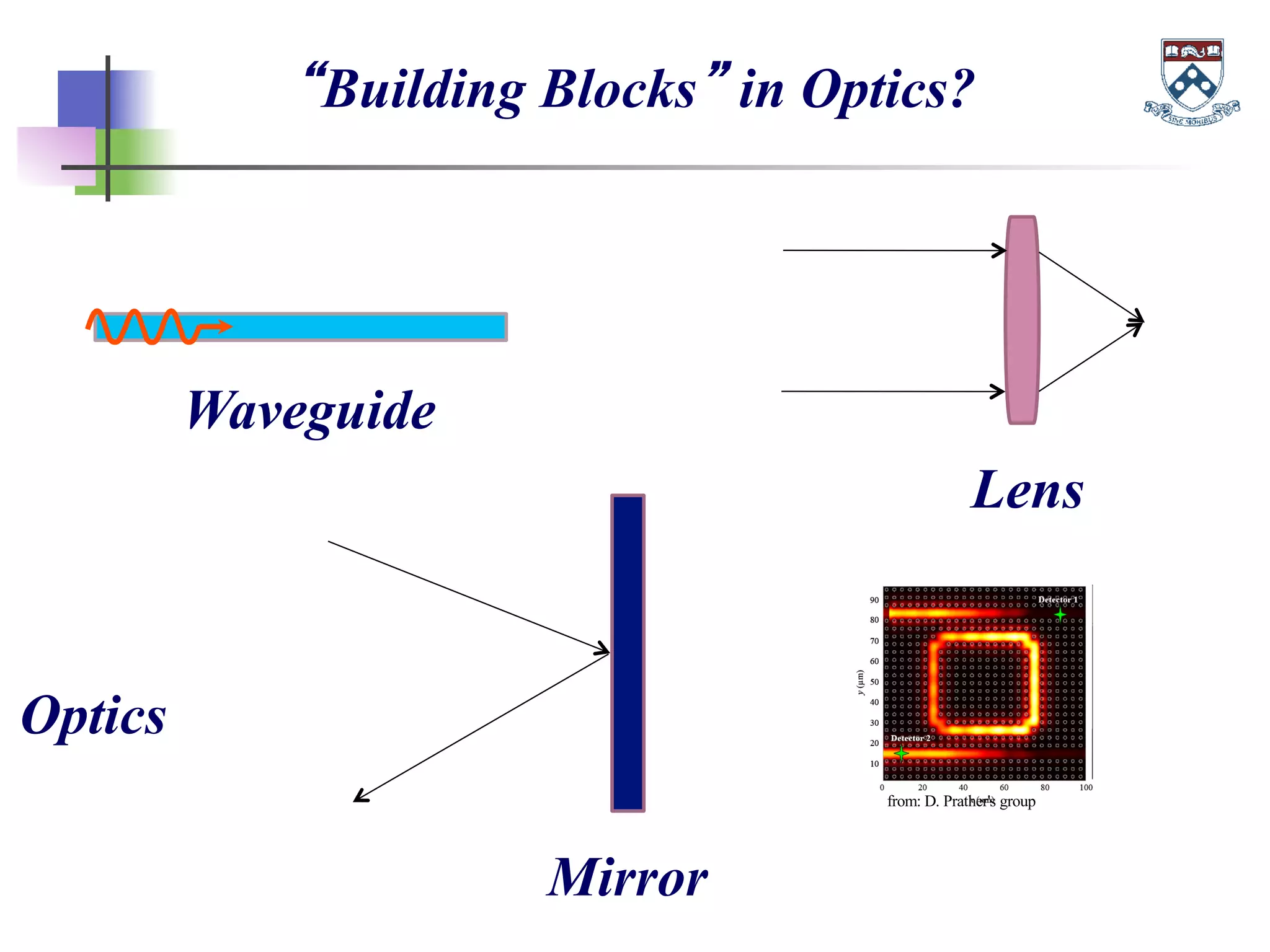
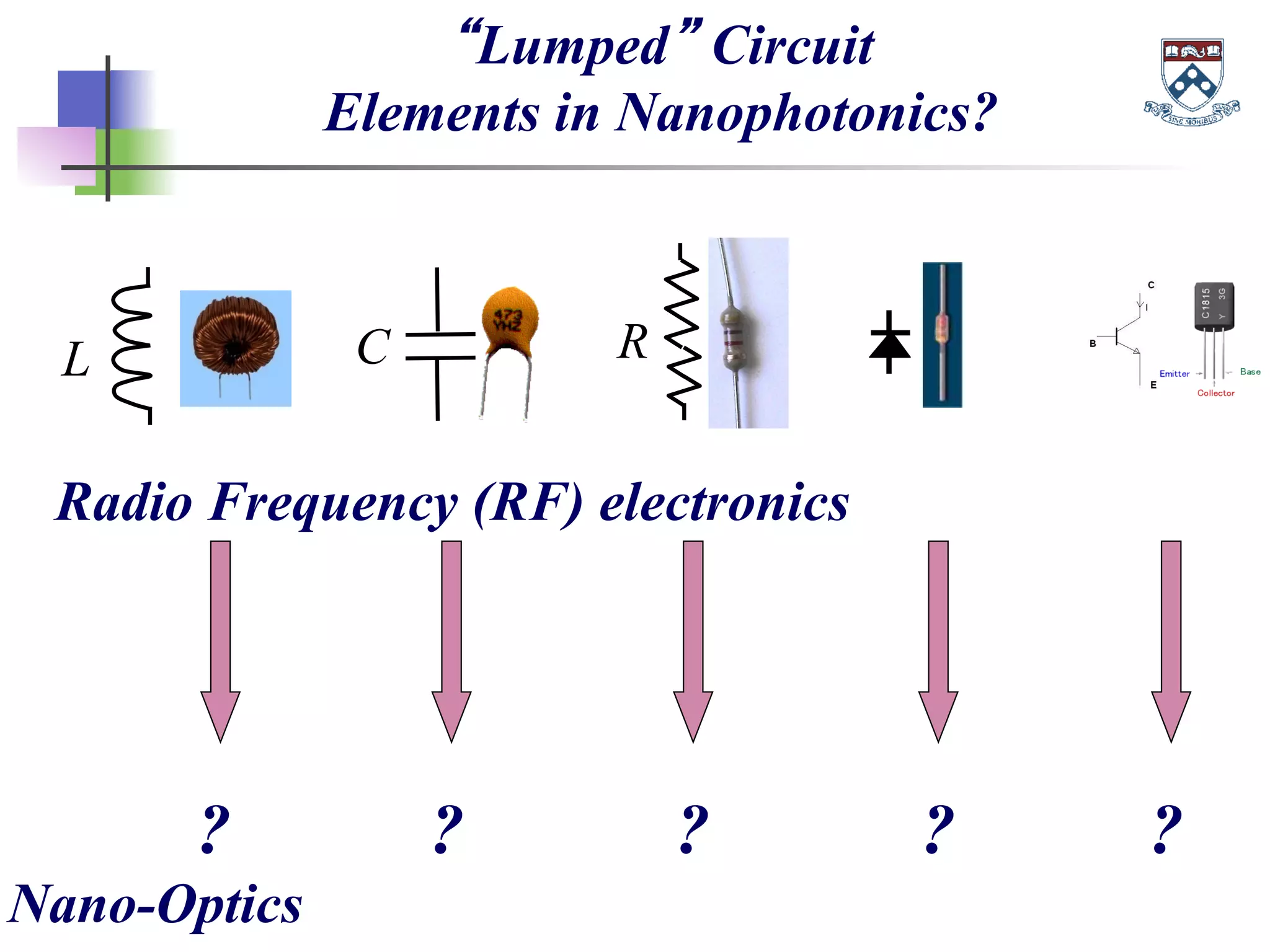
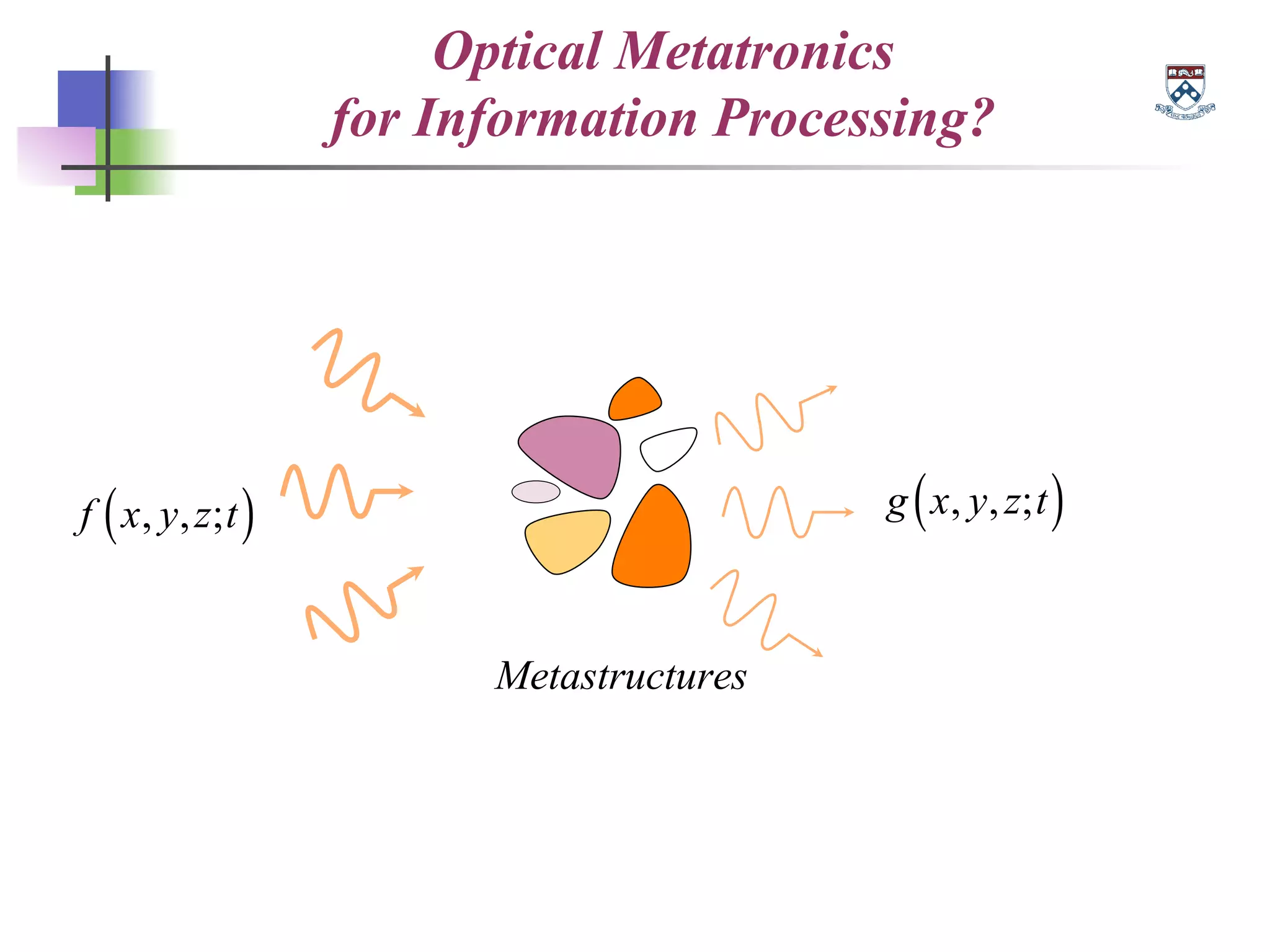
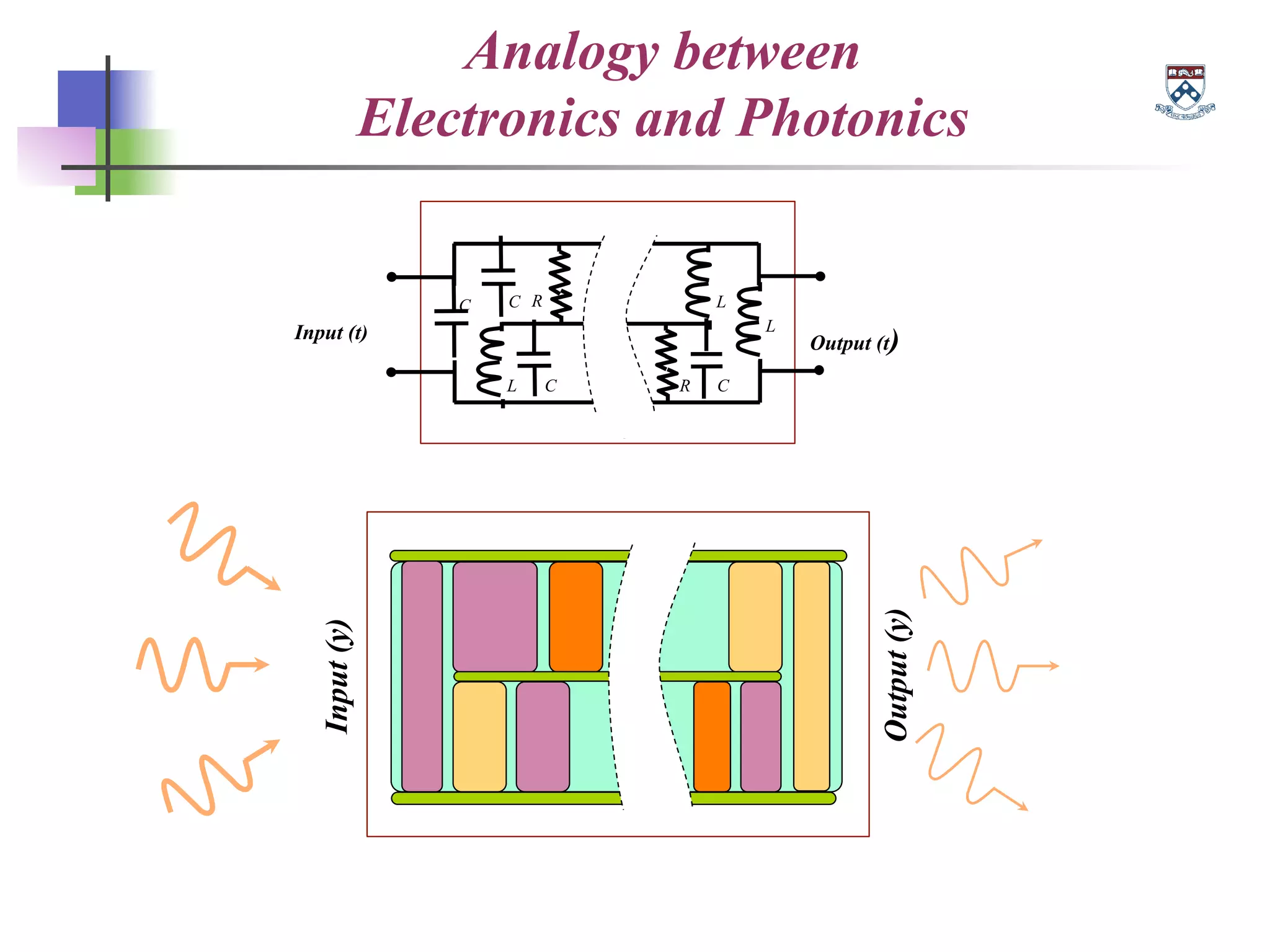
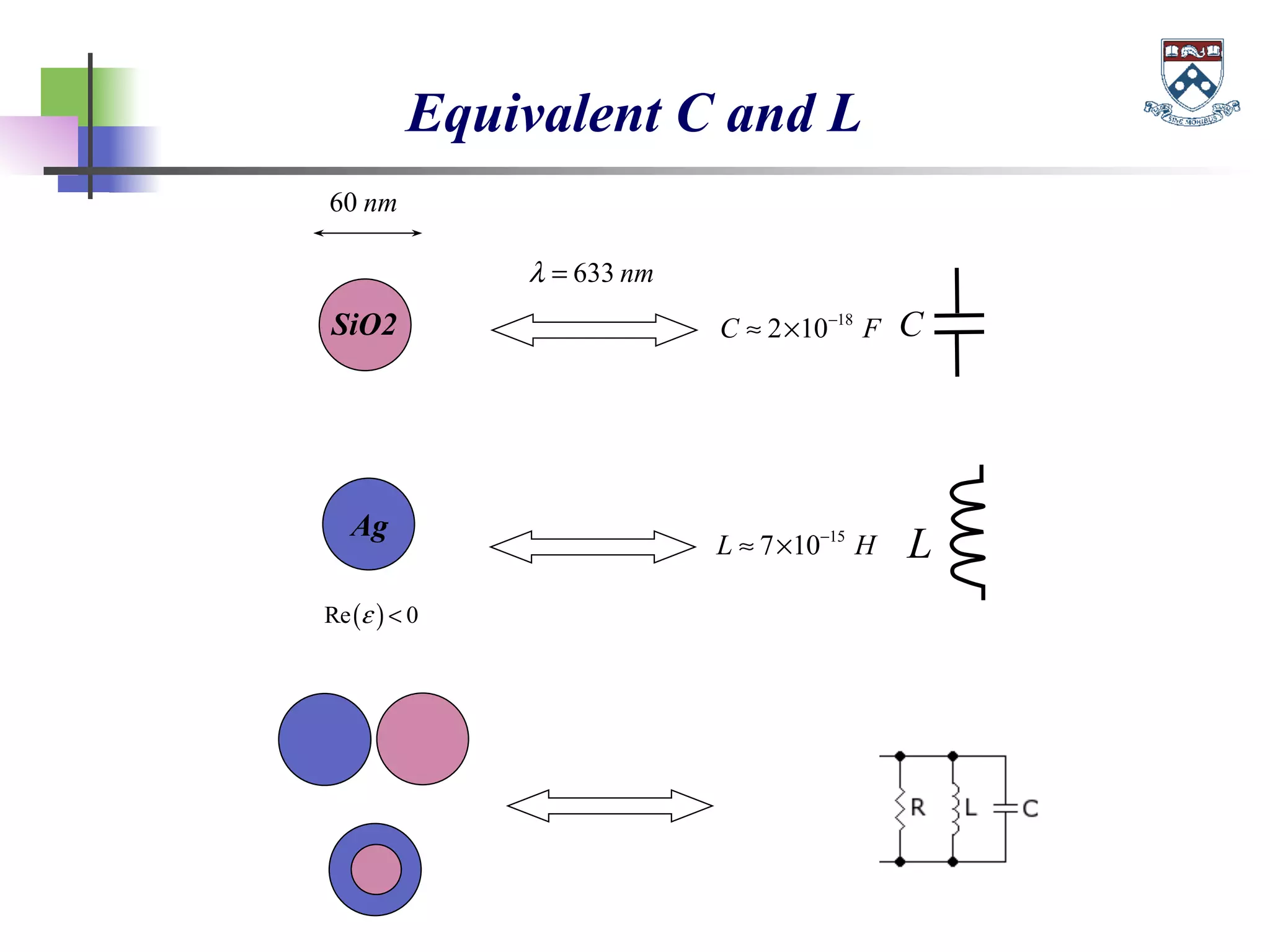
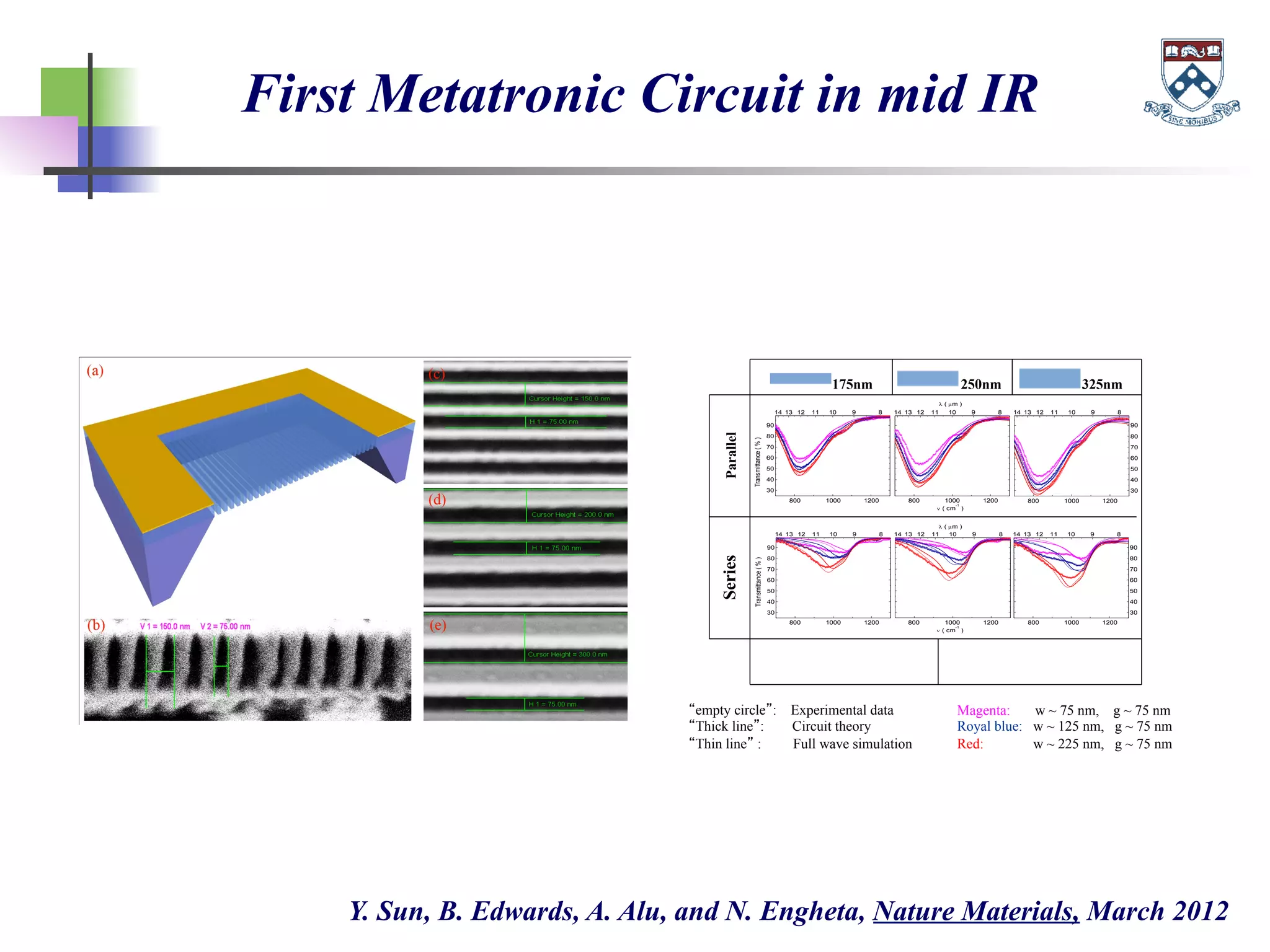
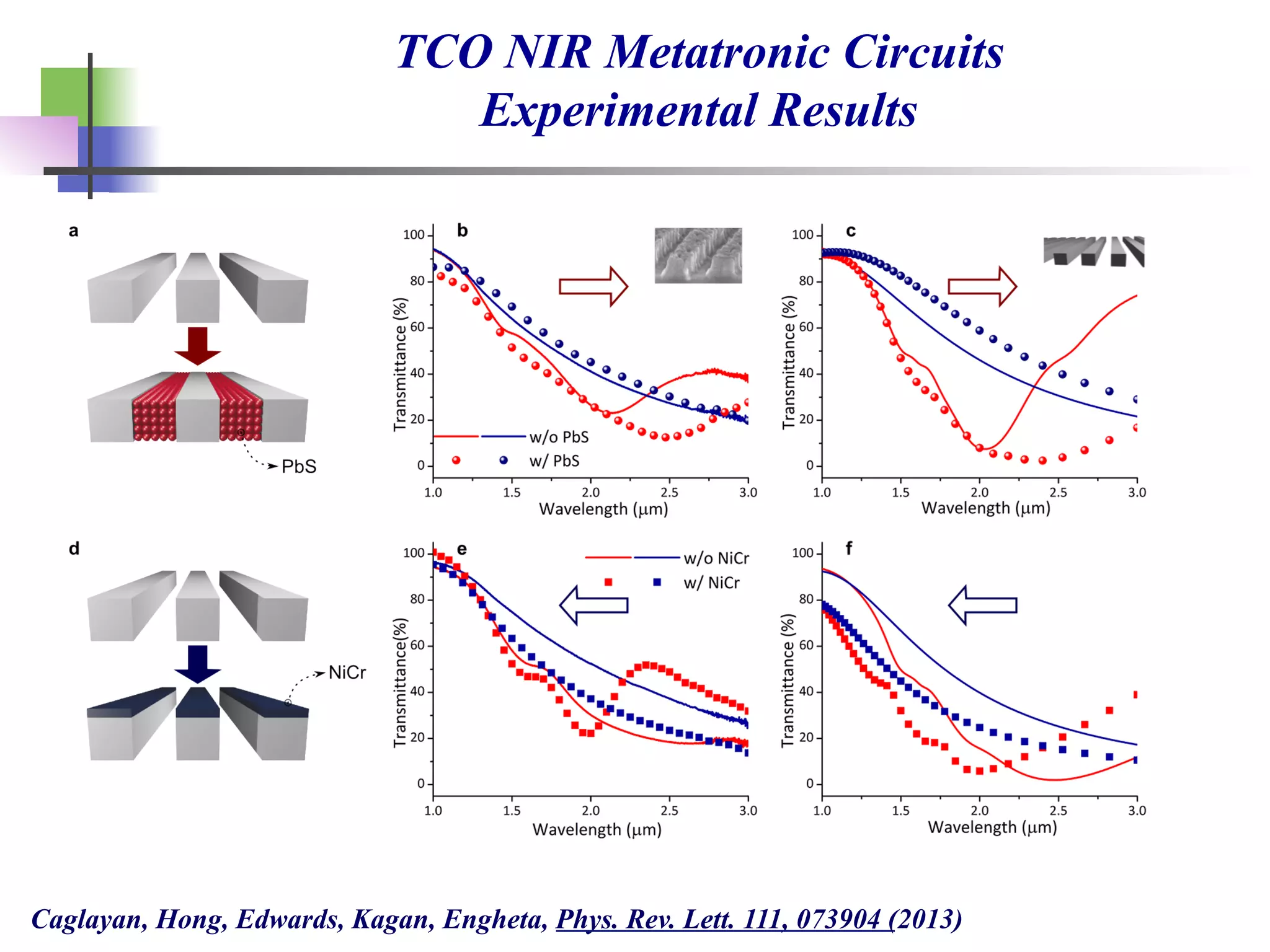
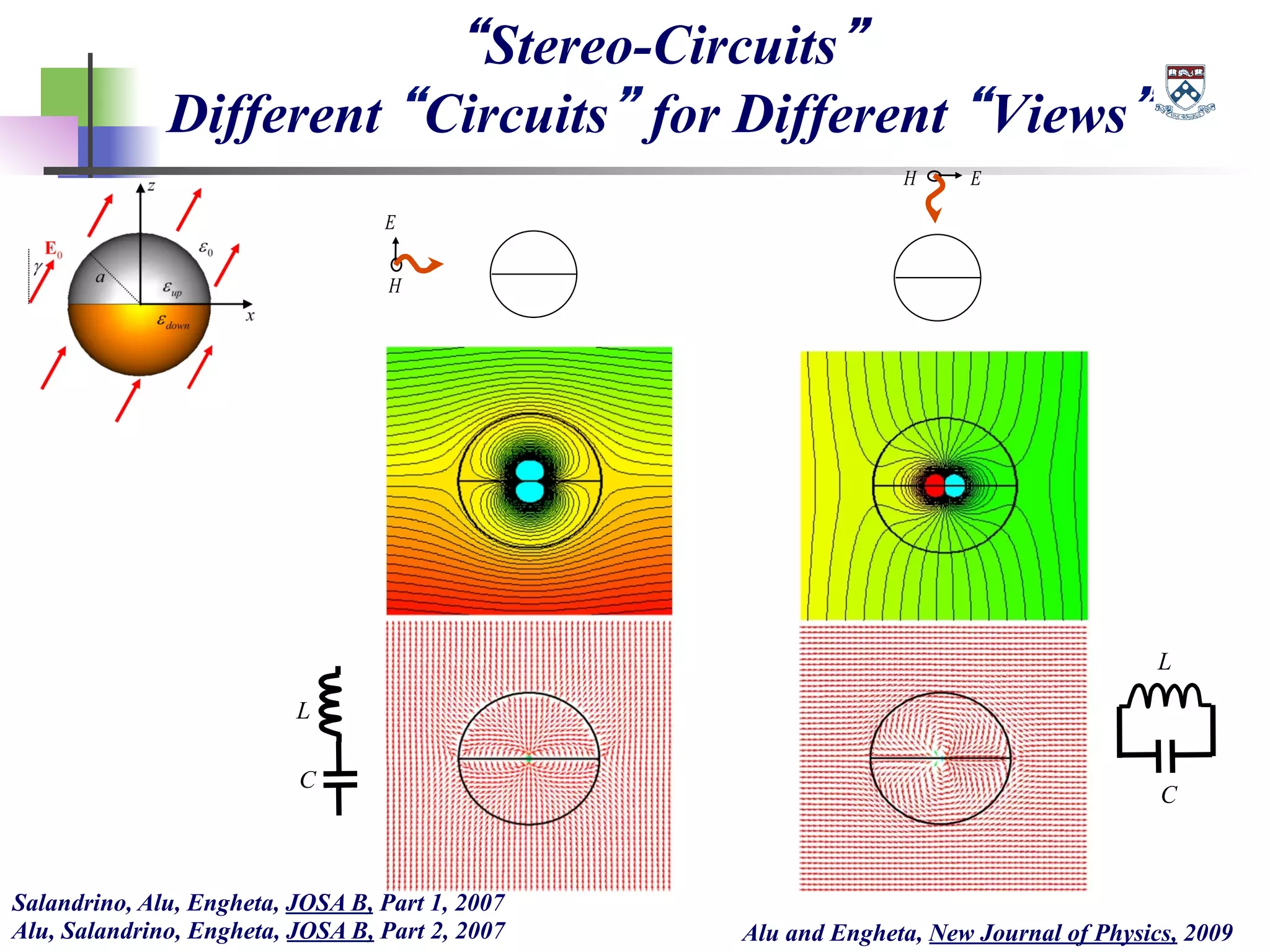
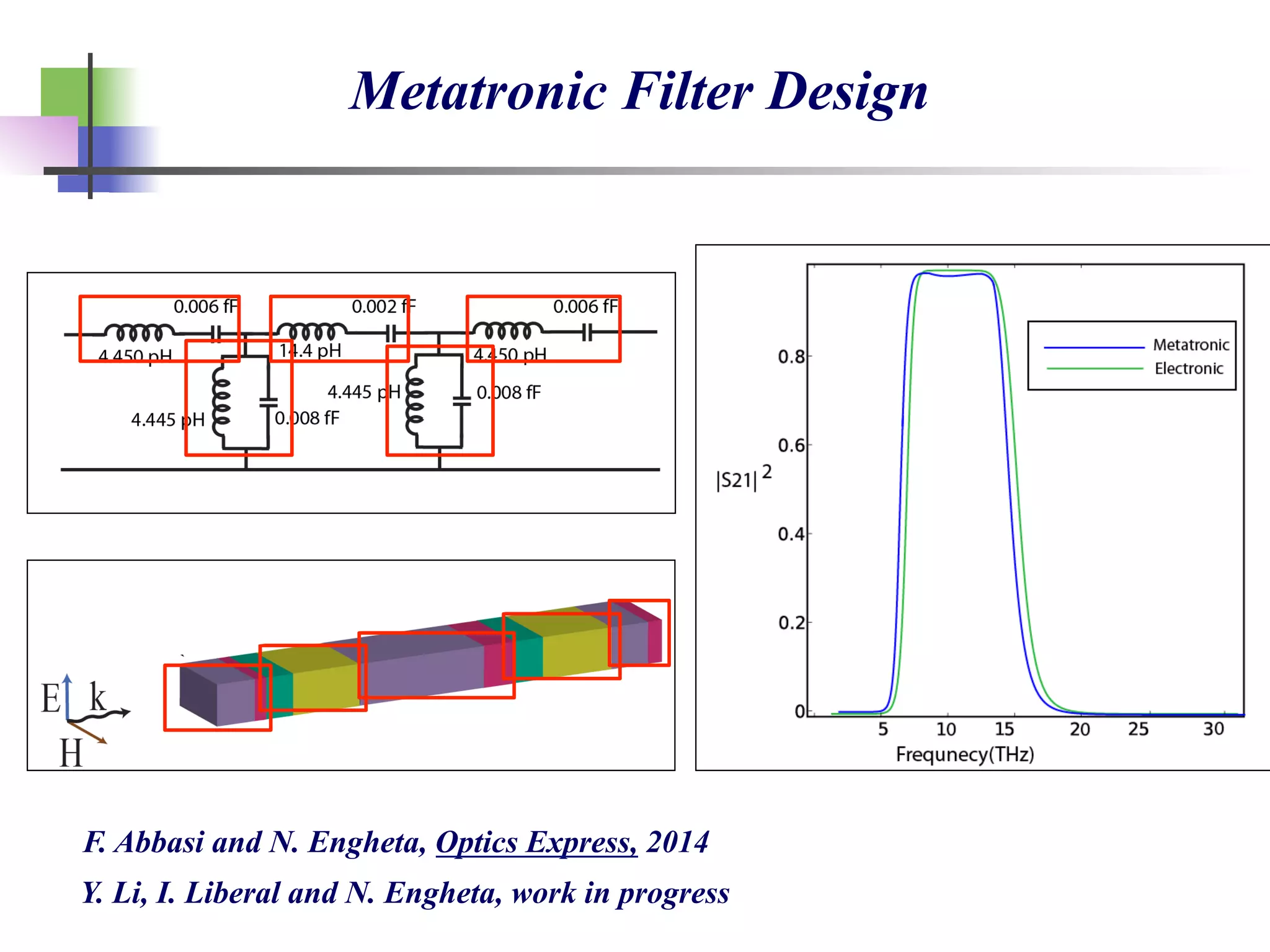
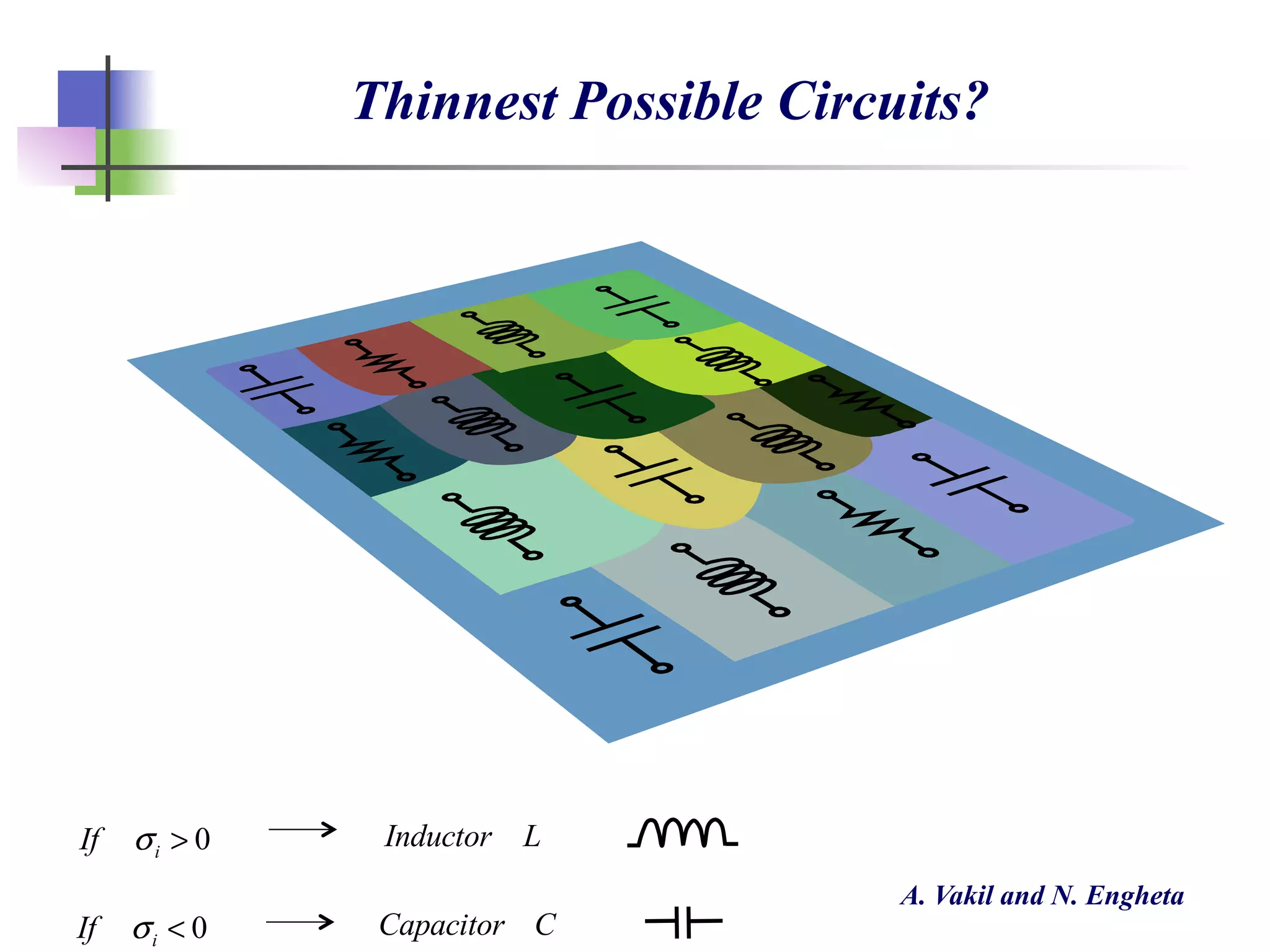
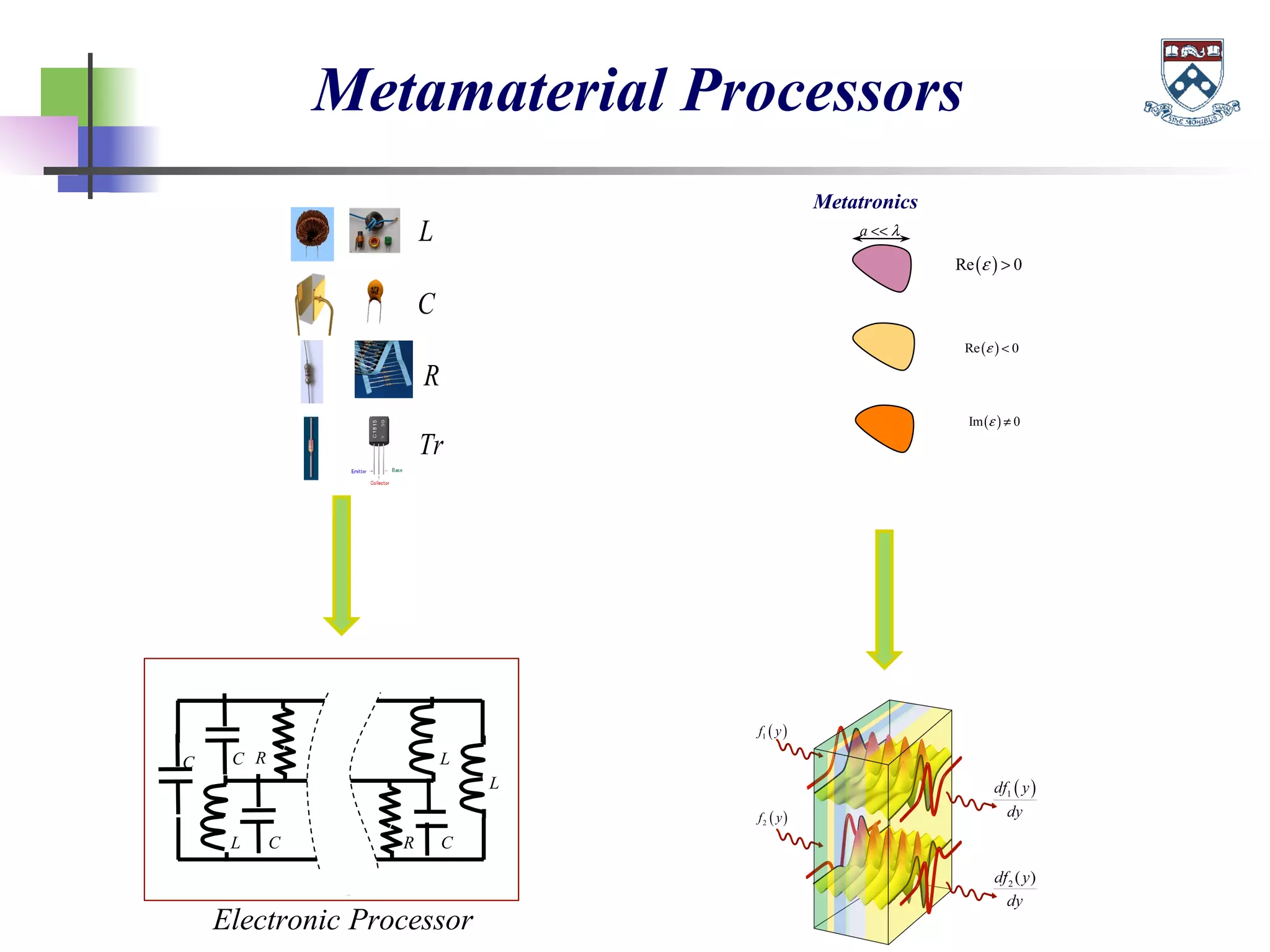
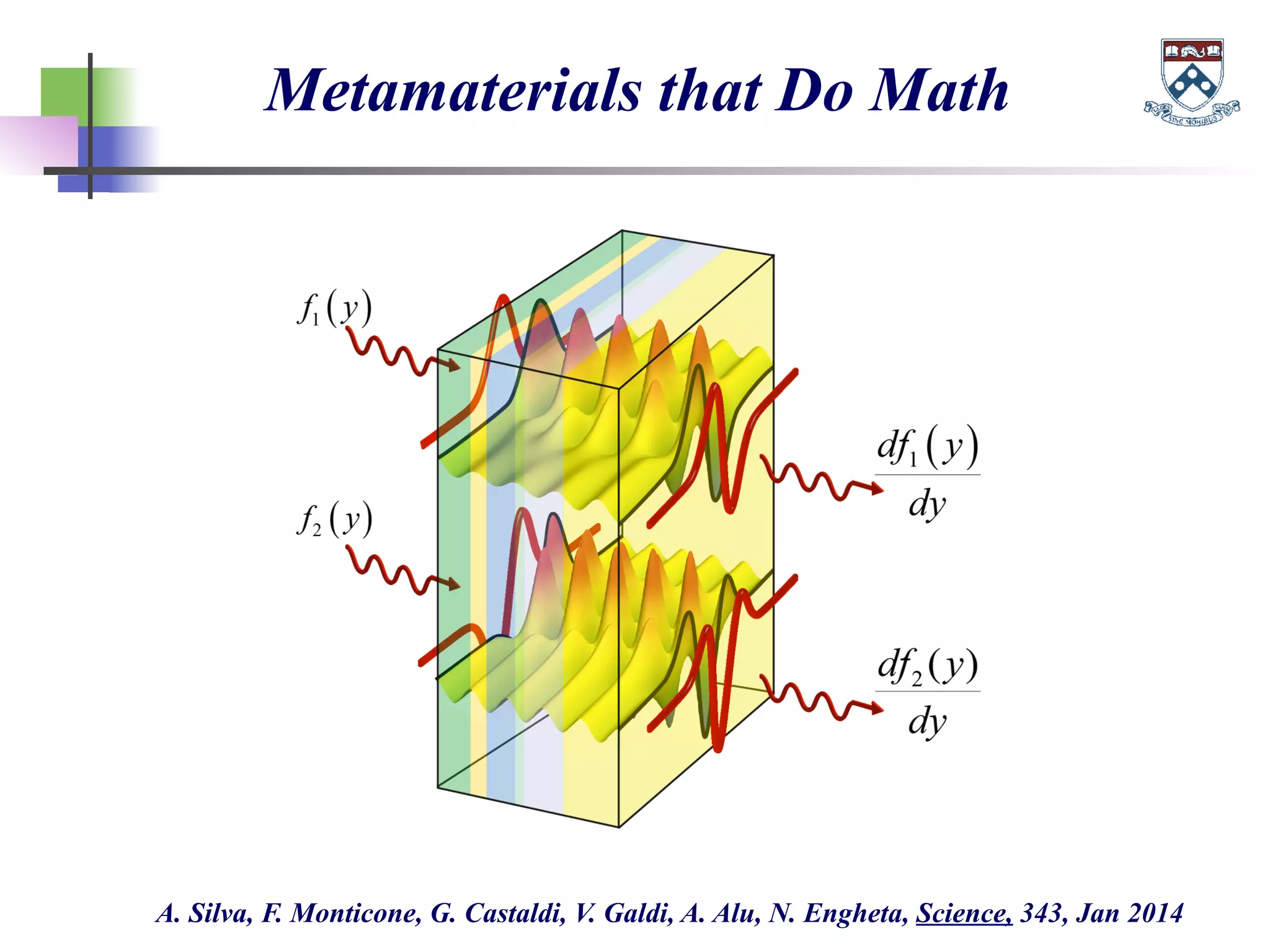
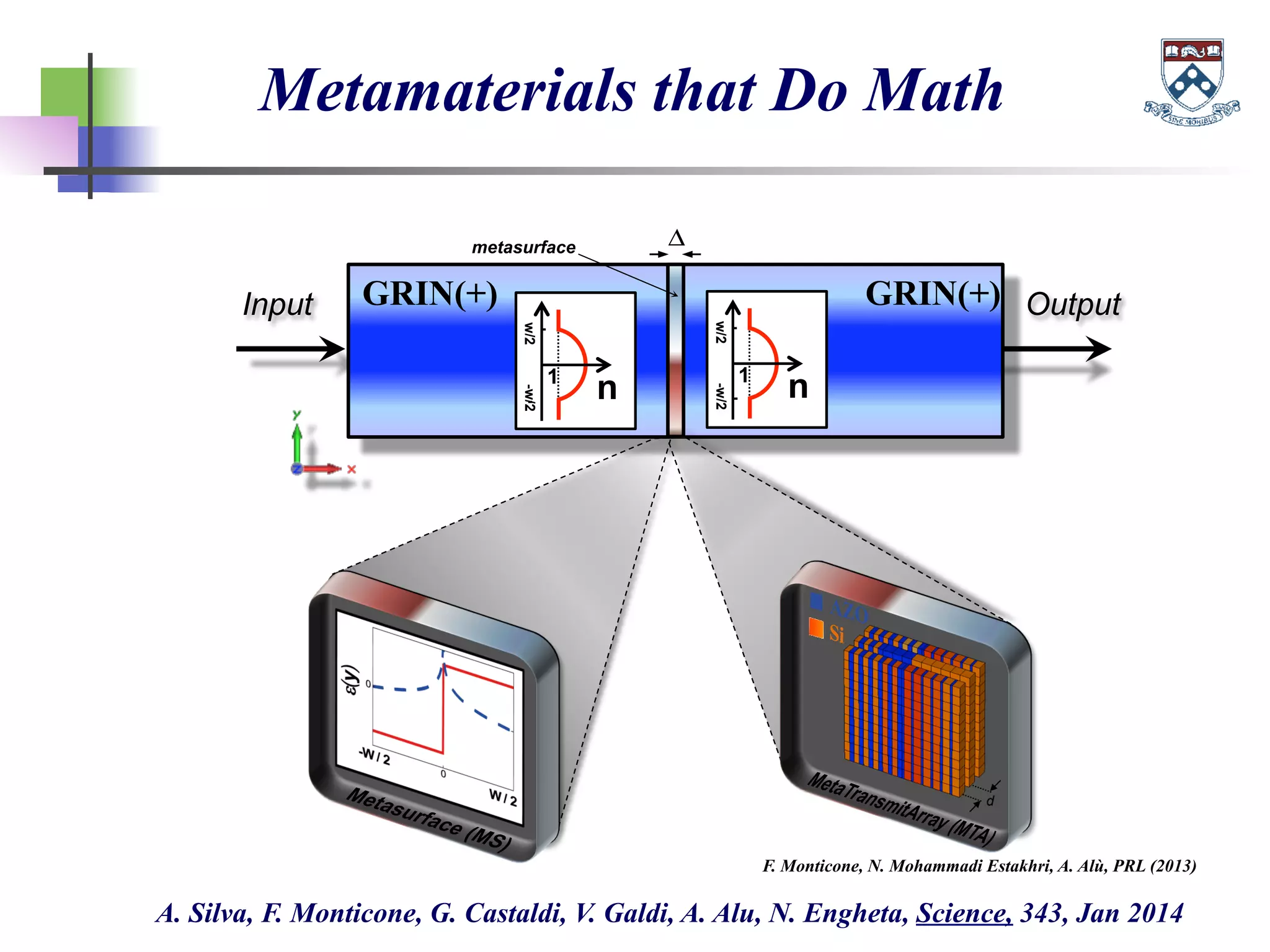
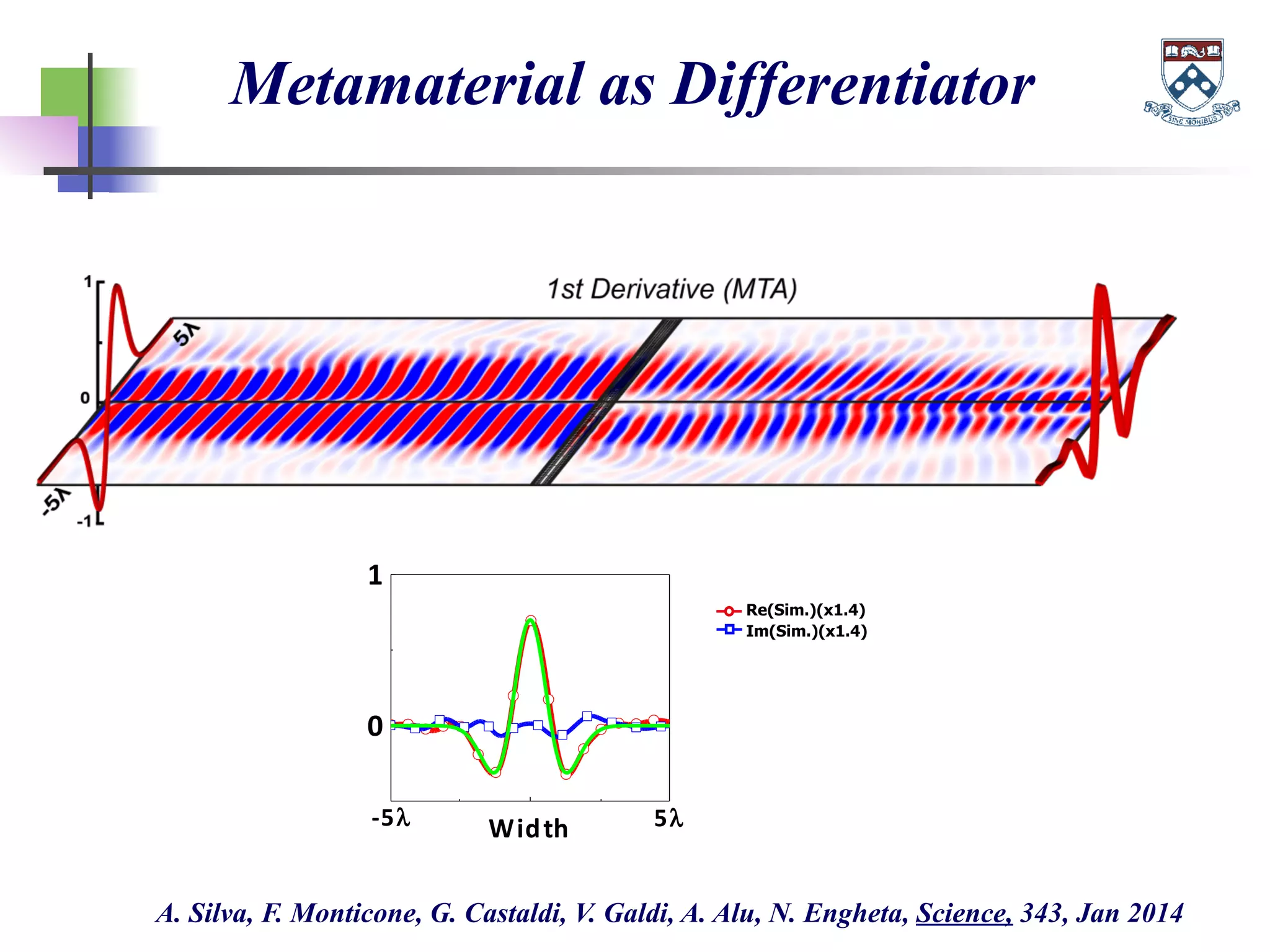
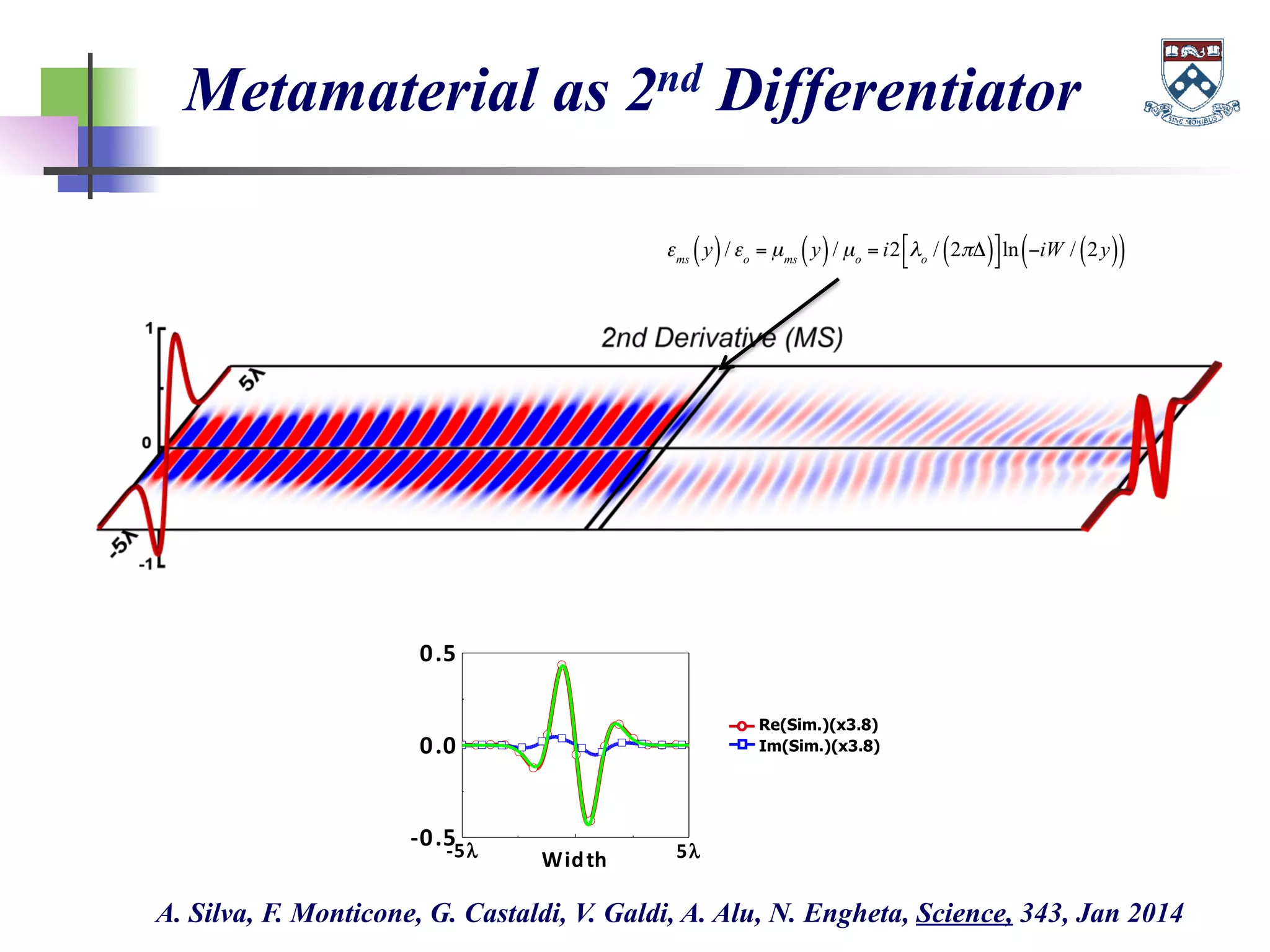
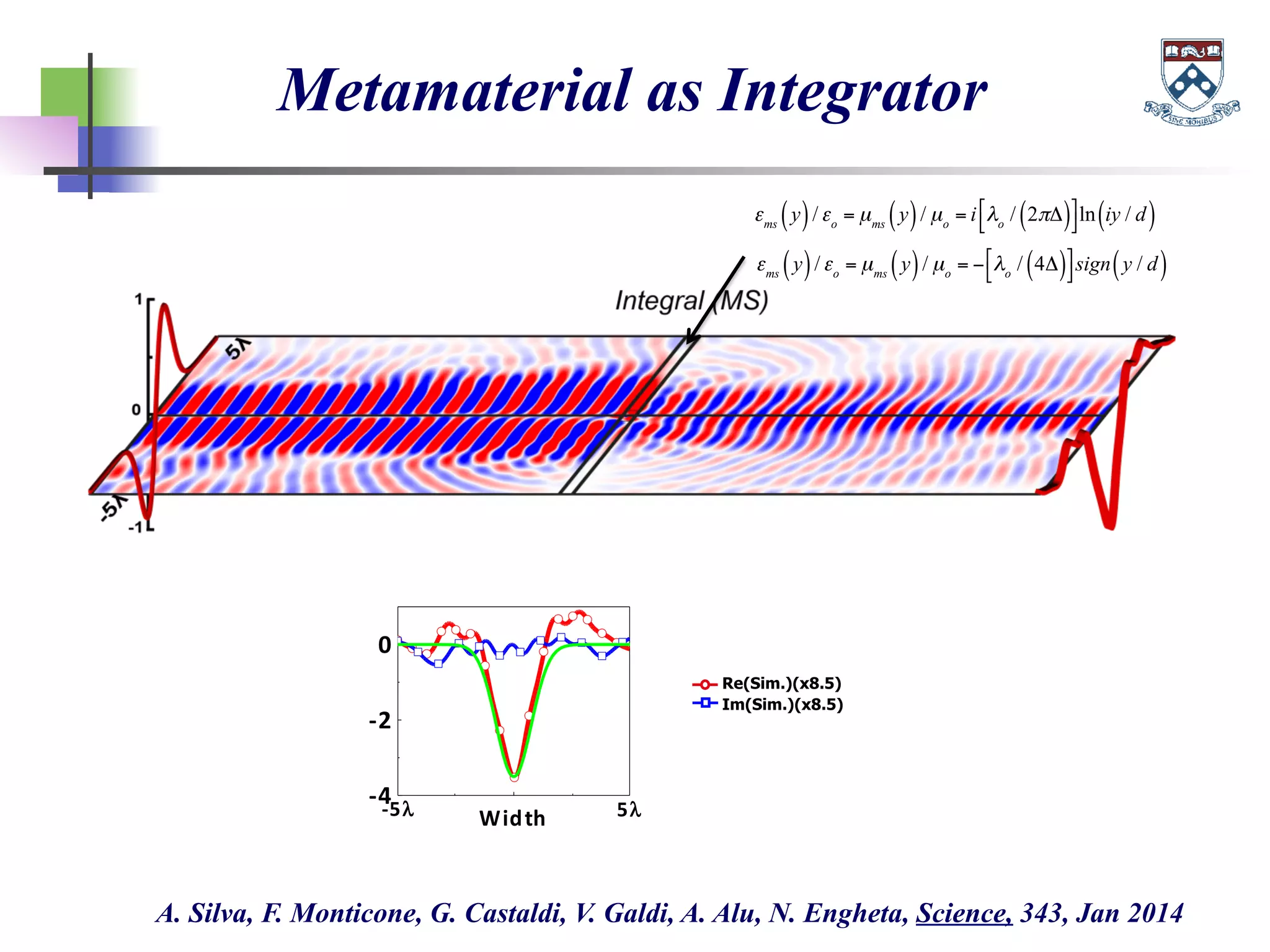
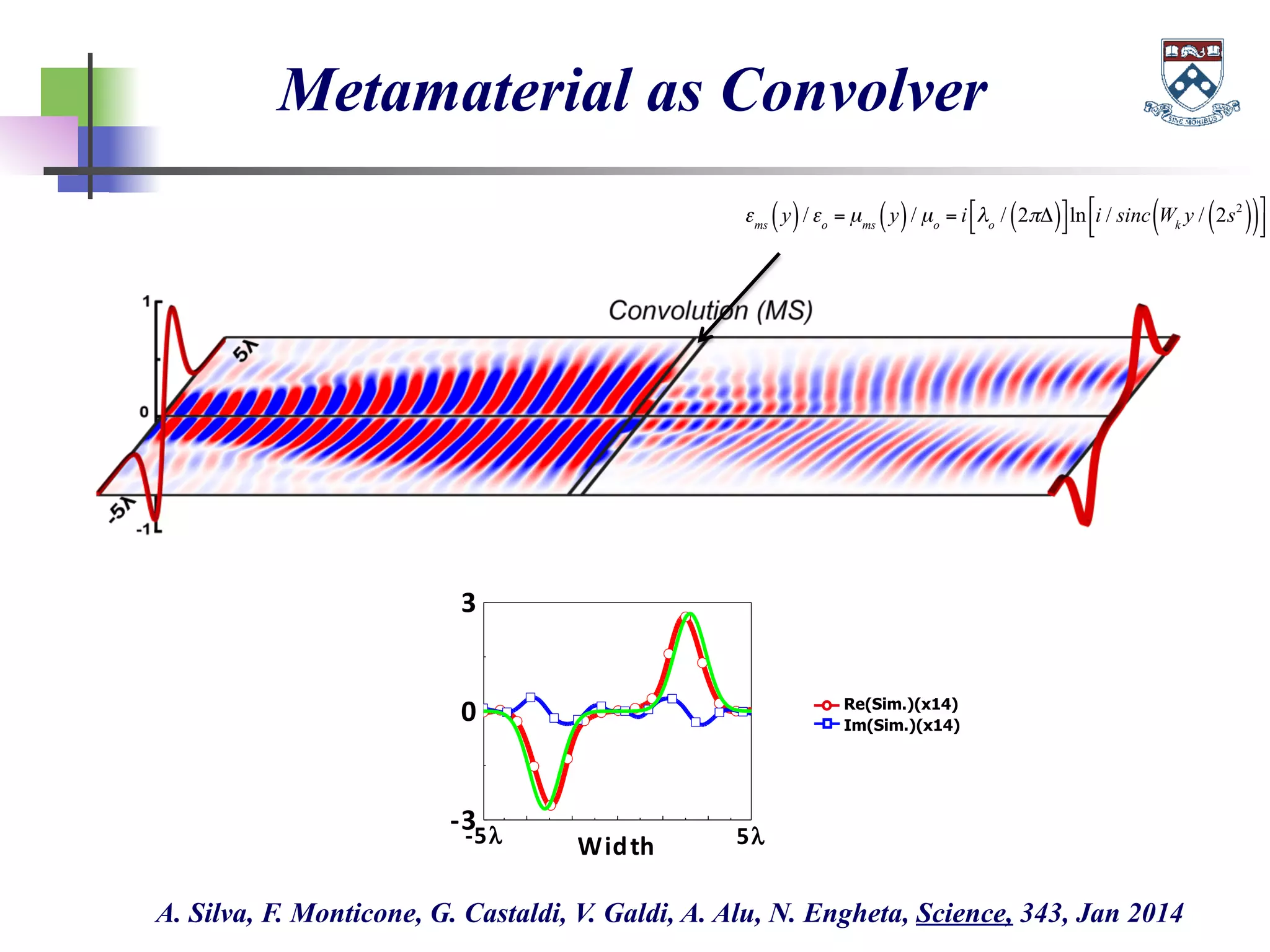
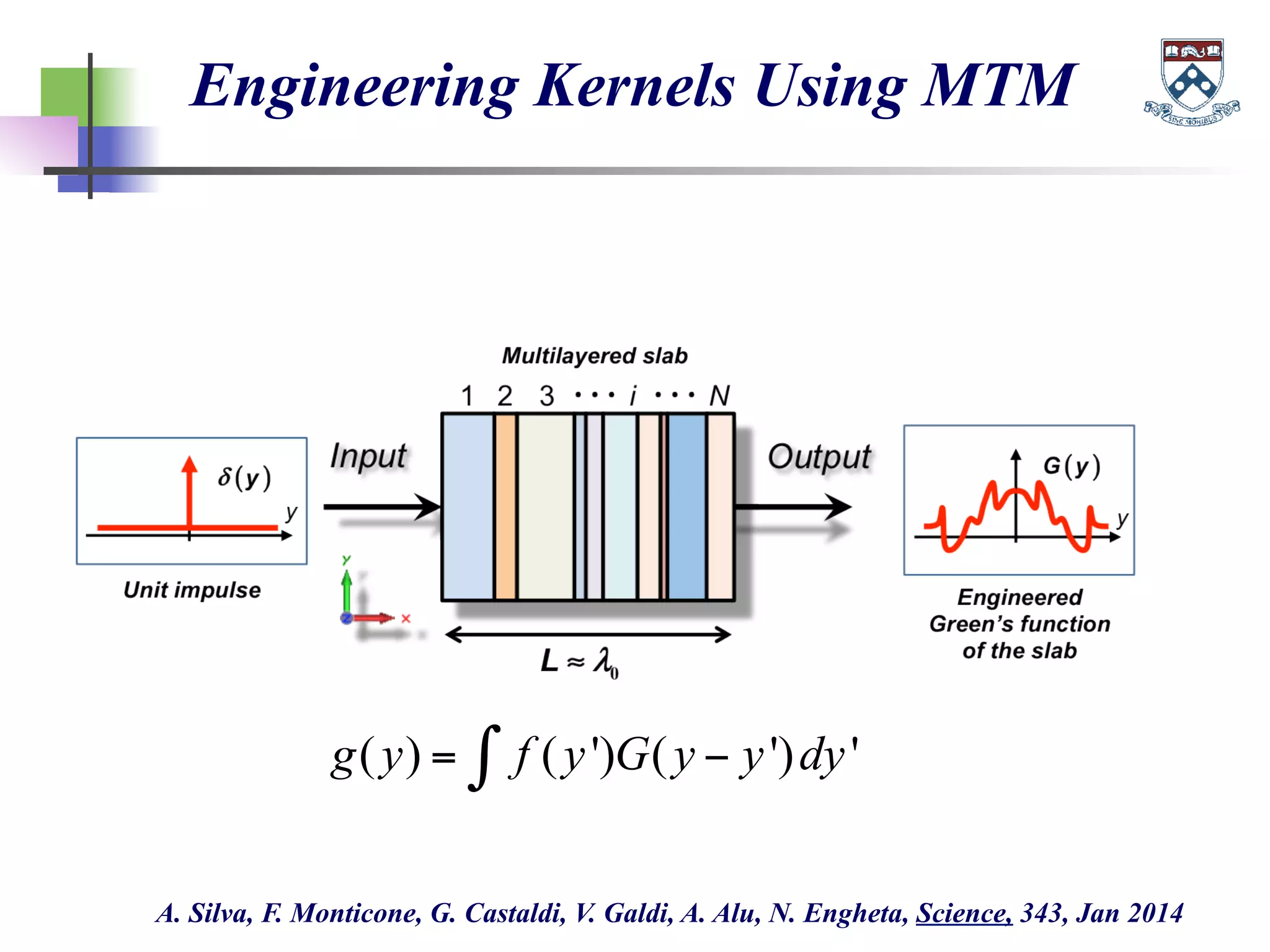
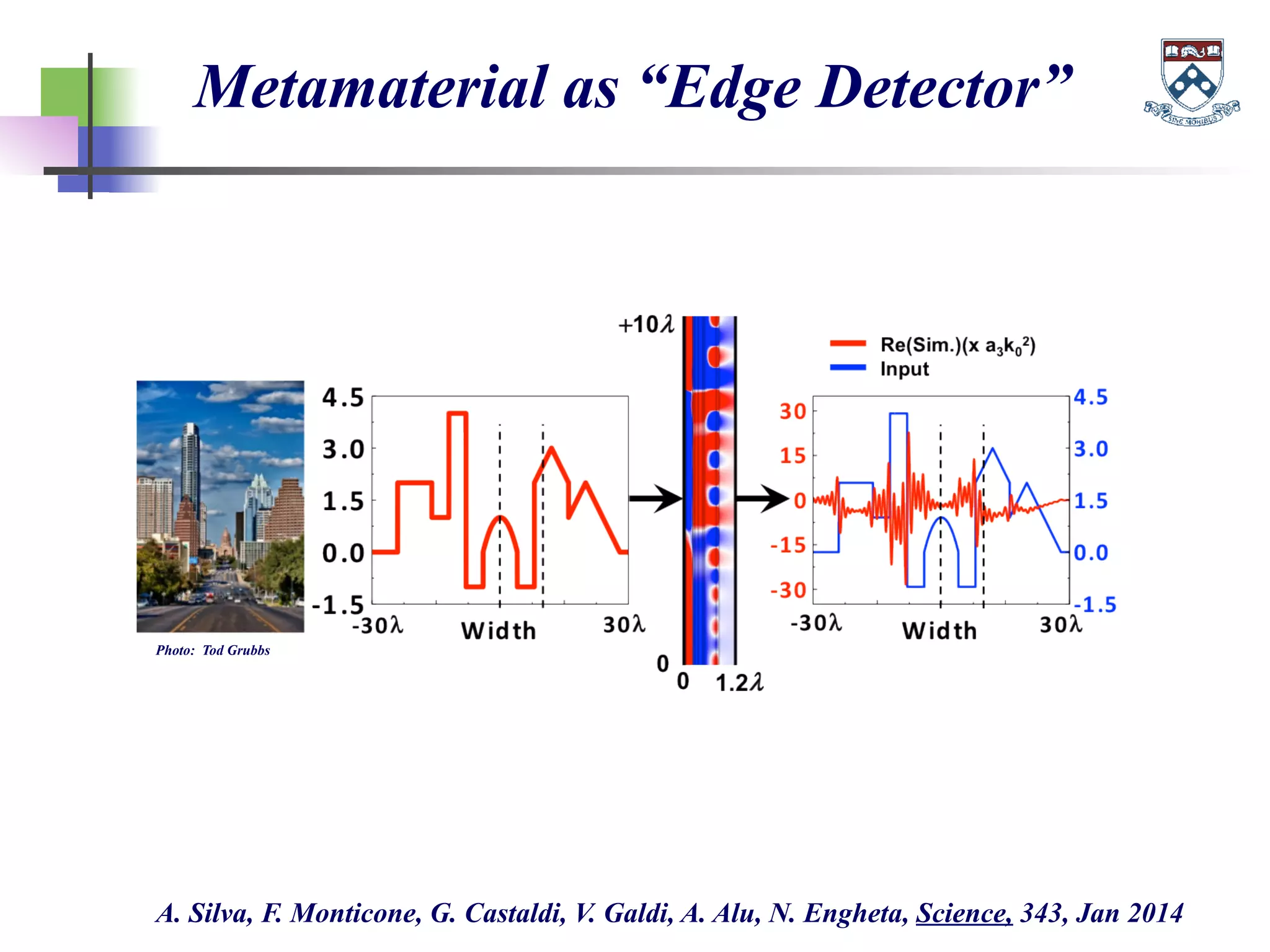
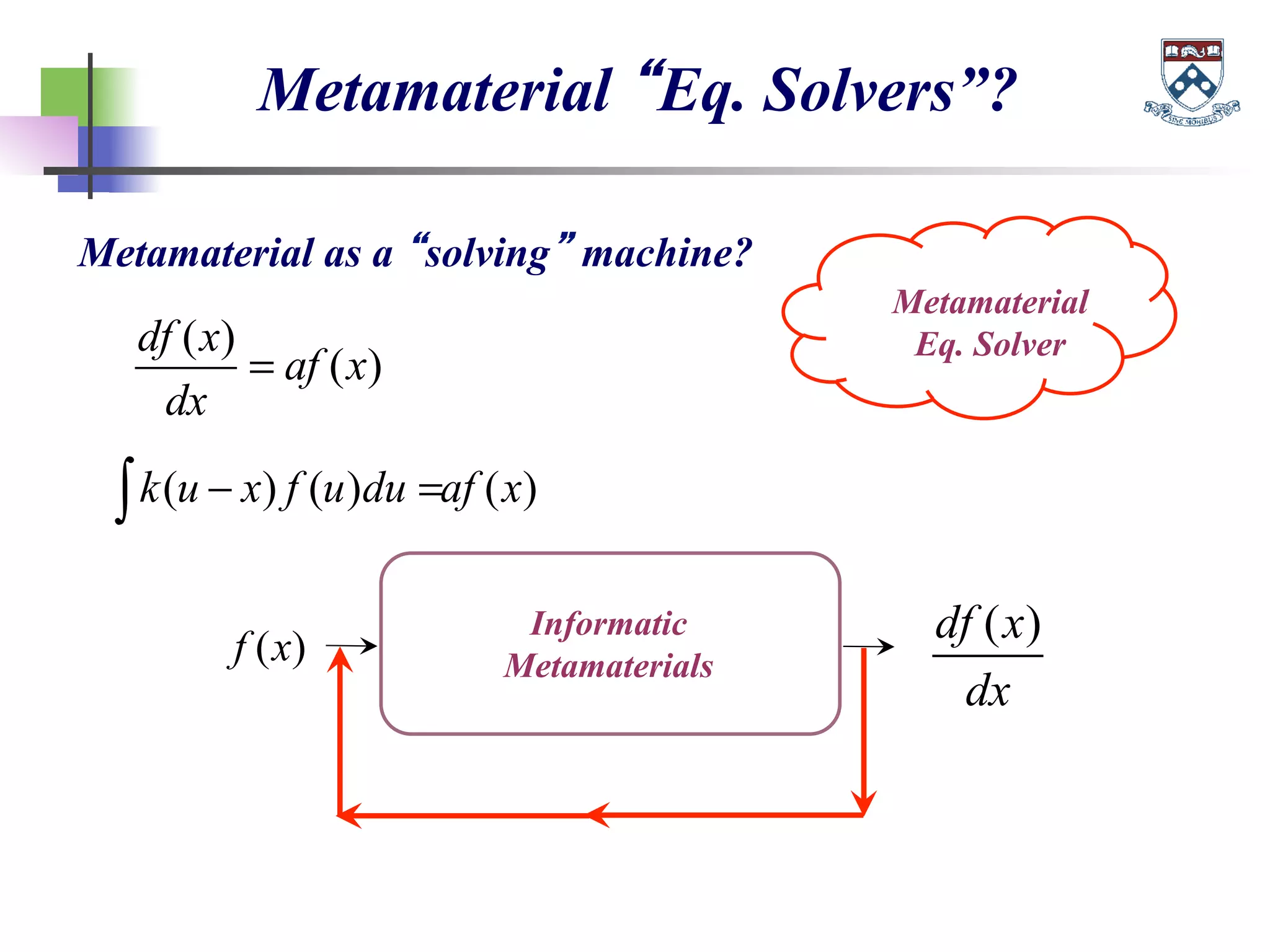
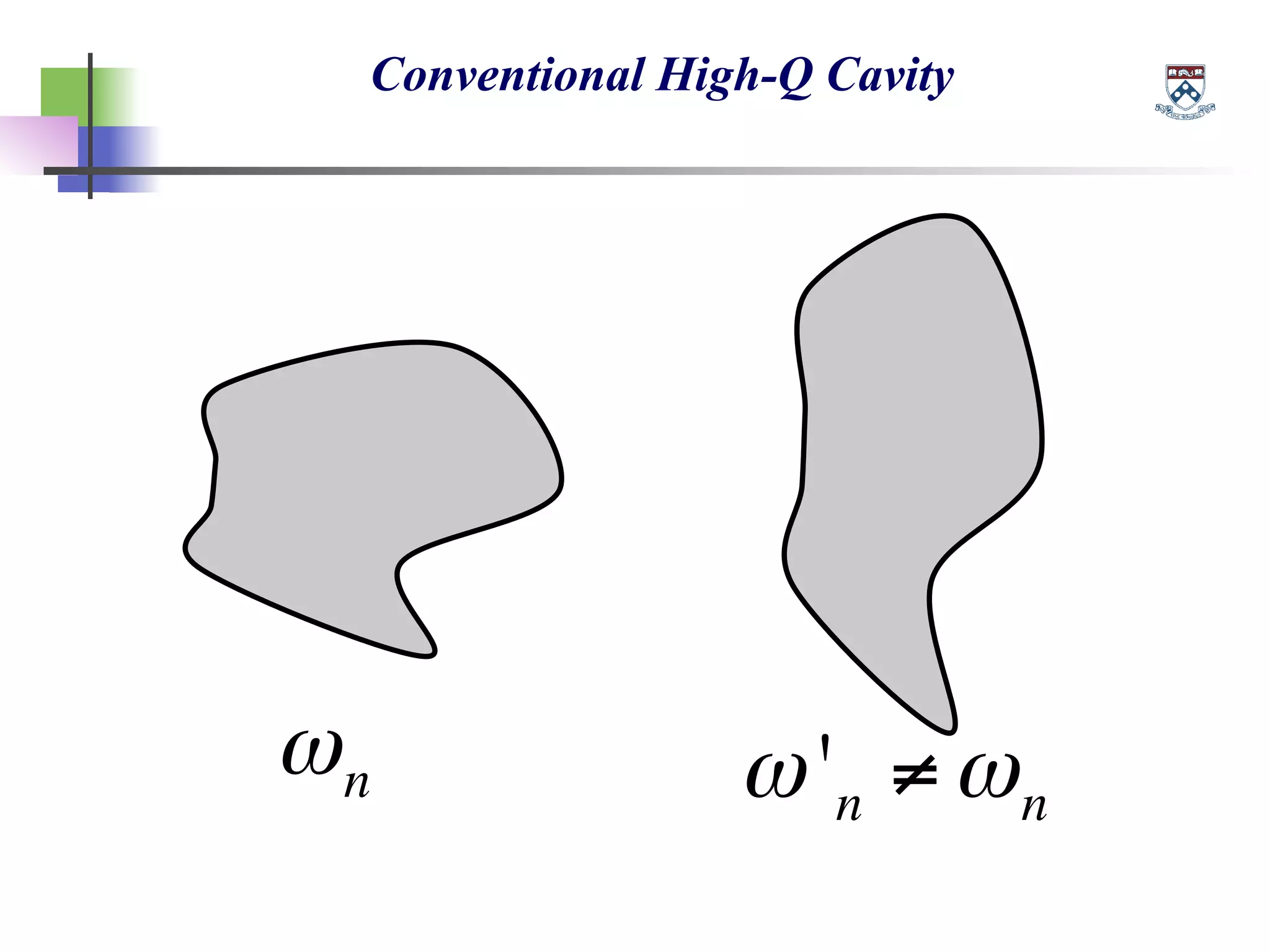
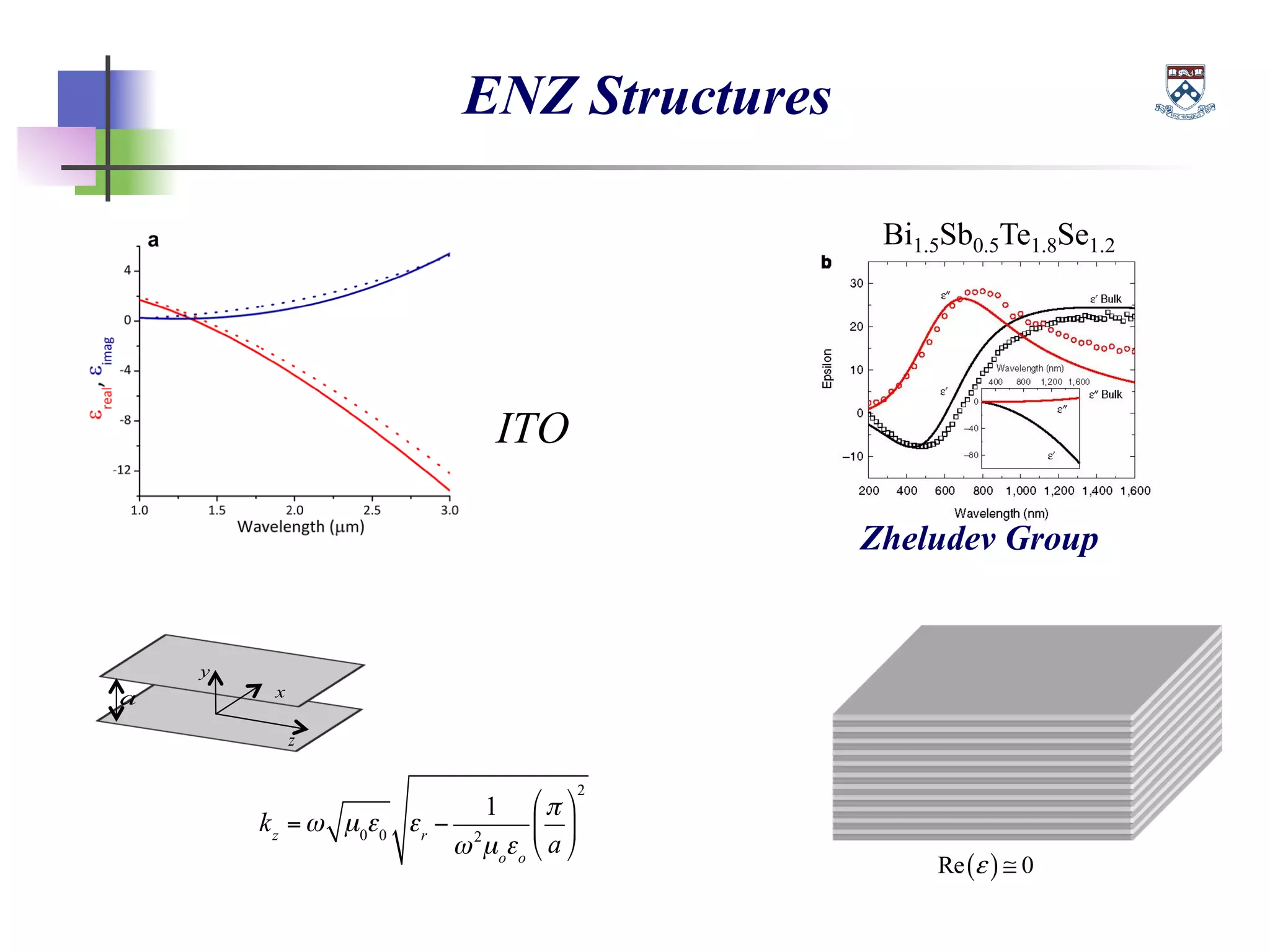
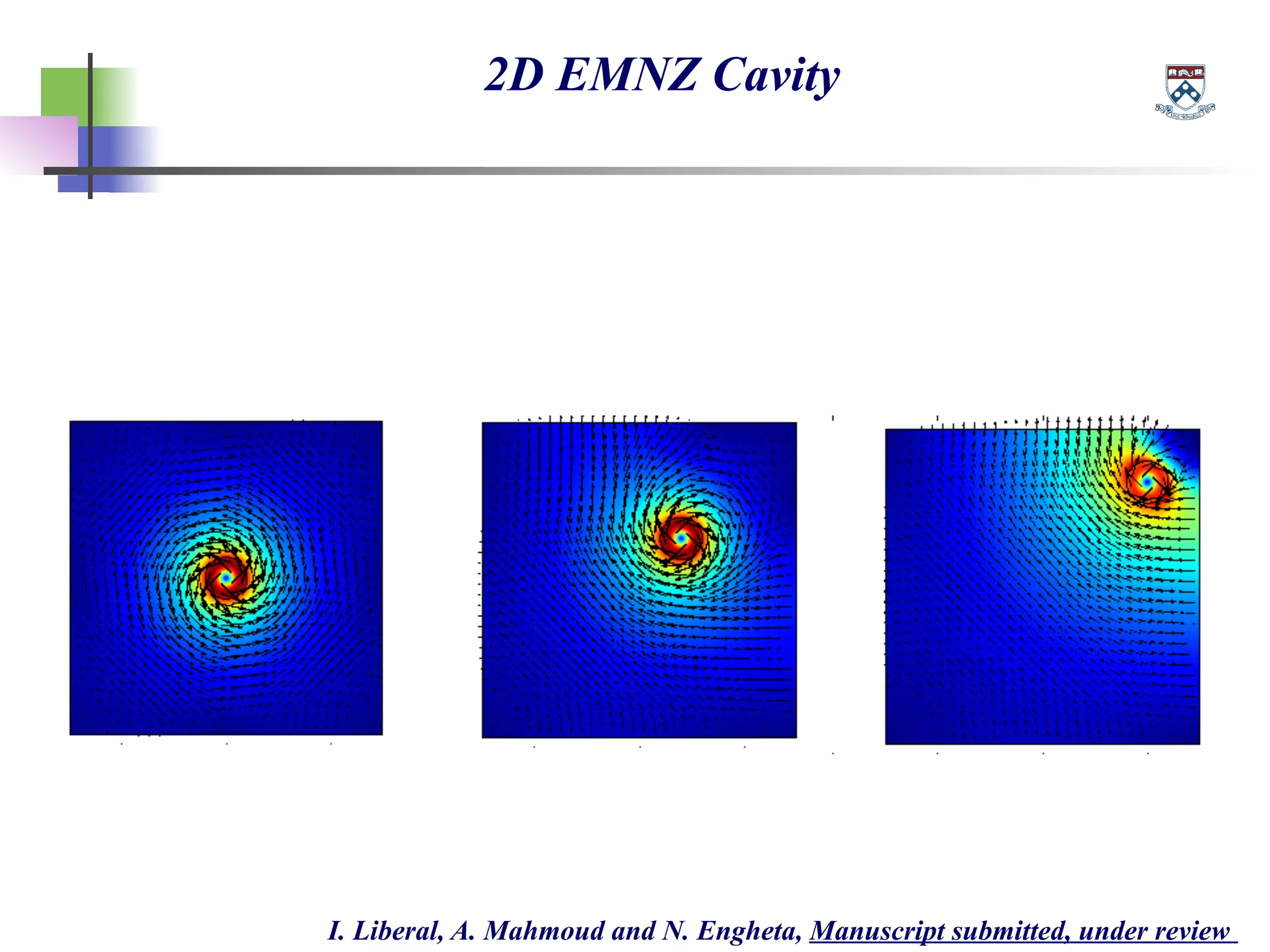
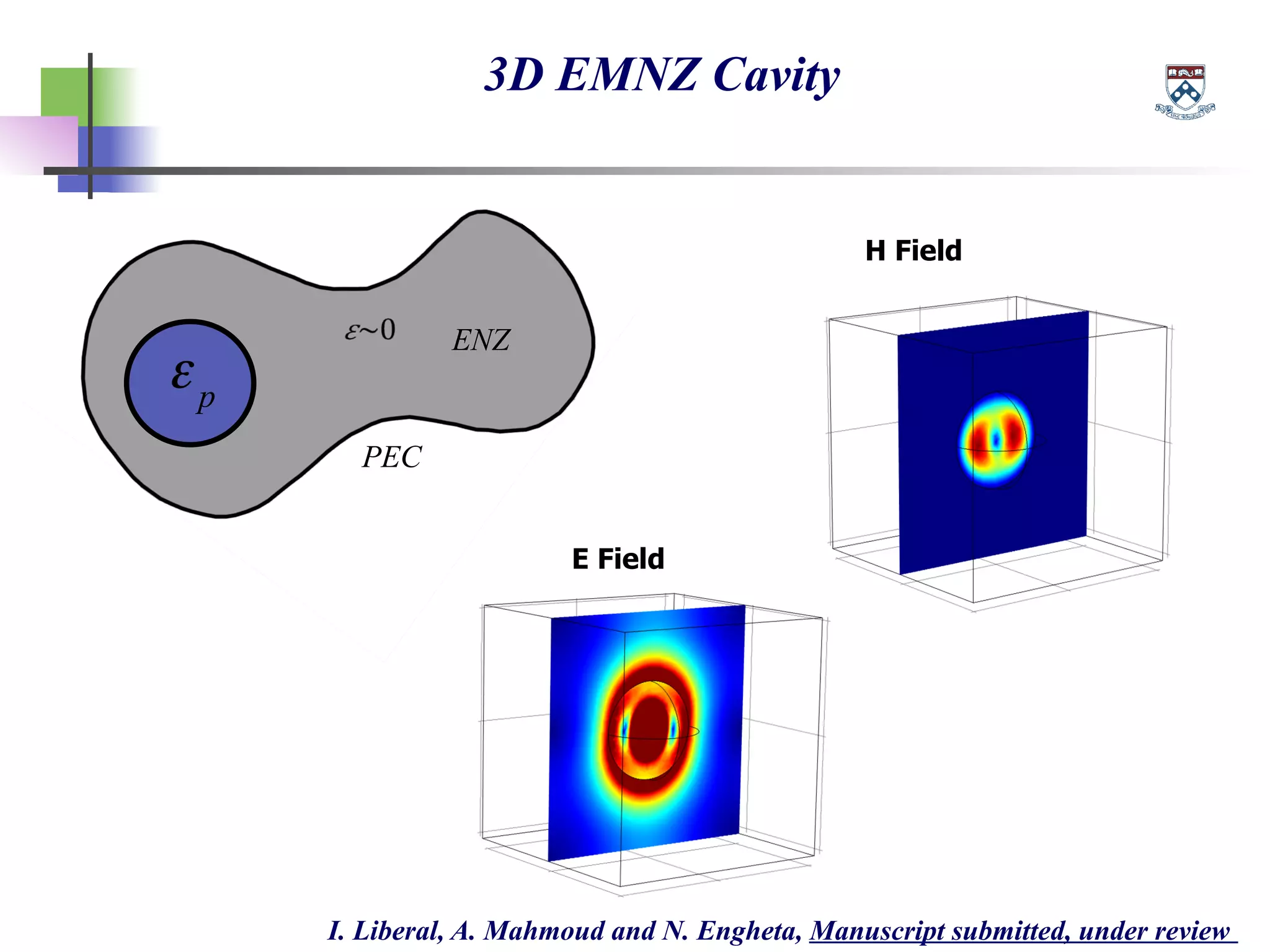
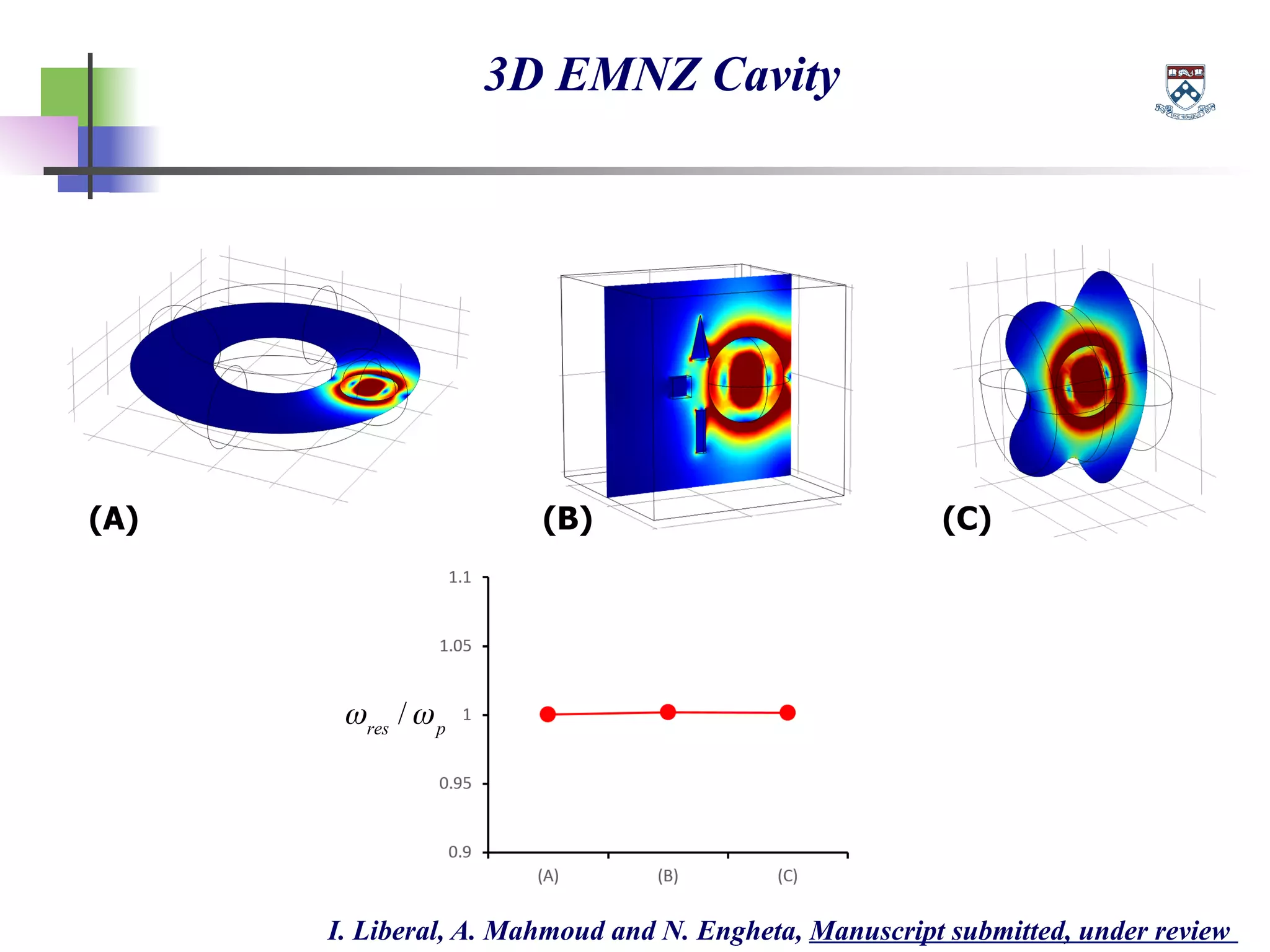
The document discusses the evolution and significance of metamaterials from 2000 to 2015, highlighting their unconventional properties and applications in areas such as cloaking, superlenses, and information processing. It emphasizes the importance of extreme dimensionality in metamaterials and presents various equations that have shaped the understanding of their functionalities. Additionally, it explores potential advancements in quantum electrodynamics and the role of metamaterials in future technological innovations.
More Related Content
Similar to From unconventional to extreme to functional materials.
More from Sociedade Brasileira de Pesquisa em Materiais
From unconventional to extreme to functional materials.
- 1. From Unconventional toExtreme to Functional Materials September 28, 2015 Nader Engheta University of Pennsylvania Philadelphia, PA, USA
- 2. 17 Equations thatChanged the World Ian Stewart, “In Pursuit of the Unknown, 17 Equations that Changed the World”, 2012
- 3. 17 Equations thatChanged the World Ian Stewart, “In Pursuit of the Unknown, 17 Equations that Changed the World”, 2012 Pythagoras’s Theorem a2 +b2 = c2 Pythagoras 530 BC Logarithms log(xy) = log(x)+log(y) Neper, 1610 Calculus df dt = lim f (t + h)− f (t) h |h→0 Newton, 1668 Law of Gravity F = G m1 m2 r2 Newton, 1687 Wave Equation ∂2 u ∂t2 = v2 ∂2 u ∂x2 D’Alambert, 1746
- 4. 17 Equations thatChanged the World Ian Stewart, “In Pursuit of the Unknown, 17 Equations that Changed the World”, 2012 Euler’s Formula for Polyhedra V − E + F = 2 Euler 1751 Normal Distributions Φ(x) = 1 2πσ e − (x−µ)2 2σ 2 Gauss 1810 Fourier Transform F(ω) = f (x)e−2πixω dx −∞ +∞ ∫ Fourier 1822 Navier-Stokes Eq Navier & Stokes, 1845ρ ∂v ∂t + v⋅∇v $ % & ' ( ) = −∇p+ ∇⋅T + f Square Root of -1 Euler, 1750i2 = −1
- 5. 17 Equations thatChanged the World Ian Stewart, “In Pursuit of the Unknown, 17 Equations that Changed the World”, 2012 Maxwell Equations ∇⋅ D = ρ ∇⋅ B = 0 ∇× E = − ∂B ∂t ∇× H = J + ∂D ∂t Maxwell 1865 2nd law of thermodynamic dS ≥ 0 Boltzmann 1874 Relativity E = mc2 Einstein, 1905 Schrodinger’s Eq. i ∂Ψ ∂t = HΨ Schrodinger 1927 Information Theory Shannon, 1949H = −∑ p(x)log p(x)
- 6. 17 Equations thatChanged the World Ian Stewart, “In Pursuit of the Unknown, 17 Equations that Changed the World”, 2012 Chaos Theory xt+1 = kxt (1− xt ) R. May 1975 Black-Scholes Eq. 1 2 σ 2 S2 ∂2 V ∂S2 + rS ∂V ∂S + ∂V ∂t − rV = 0 Black + Scholes 1990
- 7. James Clerk Maxwell’sManuscript Display in Royal Society, London, UK
- 8. James Clerk Maxwell’sManuscript Display in Royal Society, London, UK
- 9. James Clerk Maxwell’sManuscript Display in Royal Society, London, UK
- 10.
- 11.
- 12. “Artificially” Engineered Materials ●Particulate Composite Materials , ,h h r h rn ε µ= , ,c c r c rn ε µ= ● Composition ● Alignment ● Arrangement ● Density ● Host Medium ● Geometry/Shape
- 13. Metamaterials Samples (2000-2015) Smith,Schultz group (2000) Boeing group Capasso group (2011) Wegener group (2009) Zhang group (2008) Atwater group (2007) Engheta group (2012)Giessen group (2008)
- 14. Metamaterial Applications (2000-2015) Cloaking Superlens& Hyperlens Ultrathin Cavities ES AntennasTransformation Optics ENZ & MNZ Metasurfaces Metatronics
- 15. Going to the“Extreme” in Metamaterials
- 16.
- 17. From 3D Metamaterialsto 2D Metasurfaces Shalaev & Boltasseva groups (2012)Capasso group (2011) Alu group (2012) Brongersma & Hasman groups (2014) Maci group (2014) Brenner group (2014)
- 18. Ultimate Metasurface Thinnest Metamaterials http://math.ucr.edu/home/baez/graphene.jpg A.Vakil and N. Engheta, Science, 2011
- 19. One-Atom-Thick Optical Devices ,Region1: 0g iσ > ,Region 2: 0g iσ < 150c meVµ = 65c meVµ = mc =0.15eV mc =0.065eV A. Vakil and N. Engheta, Science, 2011
- 20. Experimental Verification ofMid IR Surface Wave on Graphene Basov group, Nature (2012) Koppens, Hillenbrand and Garcia de Abajo, Nature (2012)
- 21. Graphene-coated dielectric waveguide: HybridGraphene-Dielectric Systems A. Davoyan and N. Engheta, submitted under review 2D 3D “Meta-Tube”
- 22. Squeezing THz energyinto Nanoscale WG Ez 2D taper 3D taper A. Davoyan and N. Engheta, submitted under review
- 23. Information Processing atthe Extreme
- 24. “Modular Blocks” inelectronics L C R
- 25. “Building Blocks” inOptics? Optics Waveguide Lens Mirror from: D. Prather's group
- 26. “Lumped” Circuit Elements inNanophotonics? L C R Nano-Optics ? ? ? ? ? Radio Frequency (RF) electronics
- 27. Optical Metatronics: Materials BecomeCircuits Engheta, Physics Worlds, 23(9), 31 (2010) Engheta, Science, 317, 1698 (2007) Engheta, Salandrino, Alu, Phys. Rev. Lett, (2005) Sun, Edwards, Alu, Engheta, Nature Materials (2012) Electronics a λ<< ( )Re 0ε > C ( )Re 0ε < E H L ( )Im 0ε ≠ E H E H Metatronics R
- 28. Optical Metatronics for InformationProcessing? f x, y,z;t( ) Metastructures g x, y,z;t( )
- 29. Analogy between Electronics andPhotonics Input(y) Output(y) R R C C CL L L C Input (t) Output (t)
- 30. Equivalent C andL 60 nm CSiO2 18 2 10C F− ≈ × 633 nmλ = ( )Re 0ε < L Ag 15 7 10L H− ≈ ×
- 31. First Metatronic Circuitin mid IR Y. Sun, B. Edwards, A. Alu, and N. Engheta, Nature Materials, March 2012 “empty circle”: Experimental data “Thick line”: Circuit theory “Thin line” : Full wave simulation Magenta: w ~ 75 nm, g ~ 75 nm Royal blue: w ~ 125 nm, g ~ 75 nm Red: w ~ 225 nm, g ~ 75 nm 800 1000 1200 30 40 50 60 70 80 90 14 13 12 11 10 9 8 Transmittance(%) 800 1000 1200 30 40 50 60 70 80 90 14 13 12 11 10 9 8 800 1000 1200 14 13 12 11 10 9 8 λ ( µm ) ν ( cm -1 ) 800 1000 1200 14 13 12 11 10 9 8 λ ( µm ) ν ( cm -1 ) 800 1000 1200 30 40 50 60 70 80 90 14 13 12 11 10 9 8 800 1000 1200 30 40 50 60 70 80 90 14 13 12 11 10 9 8 Transmittance(%) ParallelSeries 325nm250nm175nm
- 32. TCO NIR MetatronicCircuits Experimental Results Caglayan, Hong, Edwards, Kagan, Engheta, Phys. Rev. Lett. 111, 073904 (2013)
- 33. “Stereo-Circuits” Different “Circuits” forDifferent “Views” Alu and Engheta, New Journal of Physics, 2009 EH L C E H L C Salandrino, Alu, Engheta, JOSA B, Part 1, 2007 Alu, Salandrino, Engheta, JOSA B, Part 2, 2007
- 34. Integrated Metatronic Circuits(IMC) Inspired by the work of Jack Kilby (1959) Integrated Metatronic Circuits F. Abbasi and N. Engheta, Optics Express, 2014 http://www.cedmagic.com/history/integrated-circuit-1958.html
- 35. Metatronic Filter Design Y.Li, I. Liberal and N. Engheta, work in progress F. Abbasi and N. Engheta, Optics Express, 2014
- 36. Thinnest Possible Circuits? 0iIfσ > Inductor L 0iIf σ < Capacitor C A. Vakil and N. Engheta
- 37. Metamaterial Processors L C R Tr a λ<< ()Re 0ε > ( )Re 0ε < ( )Im 0ε ≠ Metatronics R R C C CL L L C Electronic Processor
- 38. Metamaterials that DoMath A. Silva, F. Monticone, G. Castaldi, V. Galdi, A. Alu, N. Engheta, Science, 343, Jan 2014
- 39. Input OutputGRIN(+) n1 metasurface Δ GRIN(+) w/2-w/2 n1 w/2-w/2 d Metamaterialsthat Do Math A. Silva, F. Monticone, G. Castaldi, V. Galdi, A. Alu, N. Engheta, Science, 343, Jan 2014 F. Monticone, N. Mohammadi Estakhri, A. Alù, PRL (2013)
- 40. Metamaterial as Differentiator 0 1 -‐5λWidth 5λ Re(Sim.)(x1.4) Im(Sim.)(x1.4) 1 0 -1 -5λ 5λ Derivative (MS) A. Silva, F. Monticone, G. Castaldi, V. Galdi, A. Alu, N. Engheta, Science, 343, Jan 2014
- 41. Metamaterial as 2ndDifferentiator -‐0.5 0.0 0.5 -‐5λ Width 5λ Re(Sim.)(x3.8) Im(Sim.)(x3.8) 1 0 -1 -5λ 5λ Derivative (MS) εms y( )/εo = µms y( )/ µo = i2 λo / 2πΔ( )" # $ %ln −iW / 2y( )( ) A. Silva, F. Monticone, G. Castaldi, V. Galdi, A. Alu, N. Engheta, Science, 343, Jan 2014
- 42. Metamaterial as Integrator -‐4 -‐2 0 -‐5λWidth 5λ Re(Sim.)(x8.5) Im(Sim.)(x8.5) 1 0 -1 -5λ 5λ Derivative (MS) εms y( )/εo = µms y( )/ µo = i λo / 2πΔ( )" # $ %ln iy / d( ) εms y( )/εo = µms y( )/ µo = − λo / 4Δ( )# $ % &sign y / d( ) A. Silva, F. Monticone, G. Castaldi, V. Galdi, A. Alu, N. Engheta, Science, 343, Jan 2014
- 43. Metamaterial as Convolver -‐3 0 3 -‐5λWidth 5λ Re(Sim.)(x14) Im(Sim.)(x14) 1 0 -1 -5λ 5λ Derivative (MS) εms y( )/εo = µms y( )/ µo = i λo / 2πΔ( )" # $ %ln i / sinc Wk y / 2s2 ( )( )" #& $ %' A. Silva, F. Monticone, G. Castaldi, V. Galdi, A. Alu, N. Engheta, Science, 343, Jan 2014
- 44. Engineering Kernels UsingMTM g(y) = f (y')G(y − y')dy'∫ A. Silva, F. Monticone, G. Castaldi, V. Galdi, A. Alu, N. Engheta, Science, 343, Jan 2014
- 45. Metamaterial as “EdgeDetector” A. Silva, F. Monticone, G. Castaldi, V. Galdi, A. Alu, N. Engheta, Science, 343, Jan 2014 Photo: Tod Grubbs
- 46. Metamaterial “Eq. Solvers”? Metamaterial Eq.Solver Metamaterial as a “solving” machine? ( ) ( ) df x af x dx = ( ) ( ) ( )k u x f u du af x− =∫ Informatic Metamaterials( )f x ( )df x dx
- 47. “Extreme” Parameters and “Extreme”in Cavity Resonators
- 48. ωn ω'n ≠ωn ConventionalHigh-Q Cavity
- 49.
- 50.
- 51. How do wemake such EMNZ structures?
- 52. ENZ Structures ( )Re0ε ≅ ITO kz =ω µ0 ε0 εr − 1 ω2 µo εo π a ! " # $ % & 2 a z x y Bi1.5Sb0.5Te1.8Se1.2 Zheludev Group
- 53. How do wemake an EMNZ structure? M. Silveirinha and N. Engheta Physical Review B, 75, 075119 (2007) ENZ εi >1 µeff = µo Acell Ah,cell + 2πR2 J1 ki R( ) ki RJ0 ki R( ) ! " # # $ % & & A. Mahmoud and N. Engheta, Nature Communications, Dec 2014 CT Chan’s group Nature Materials, 10, 582-585 (2011)
- 54. 2D EMNZ Cavity I.Liberal, A. Mahmoud and N. Engheta, Manuscript submitted, under review
- 55. 2D EMNZ Cavity I.Liberal, A. Mahmoud and N. Engheta, Manuscript submitted, under review
- 56. 3D EMNZ Cavity εp PEC ENZ HField E Field I. Liberal, A. Mahmoud and N. Engheta, Manuscript submitted, under review
- 57. 3D EMNZ Cavity (A)(B) (C) ωres /ωp I. Liberal, A. Mahmoud and N. Engheta, Manuscript submitted, under review
- 58. EMNZ in QuantumElectrodynamics Superradiance? Subradiance? Long-Range Collective States of Multi-emitters? Long-Range Entanglement? Cavity QED?
- 59. Summary Metamaterials can performprocessing, functionality at the compact scale Metamaterials can play important roles in quantum electrodynamics Sculpting waves using extreme scenarios can play interesting roles Metatronic Processing Quantum MTM One-Atom-Thick Optical Devices !
- 60. Thank you verymuch