This thesis explores advanced traveler information systems (ATIS) for improving road traffic monitoring and routing efficiency while addressing increasing infrastructure demands. It introduces a new non-first-in-first-out (non-FIFO) routing algorithm that balances the fastest travel times with incident risk minimization, along with mathematical models for estimating traffic volumes and incident probabilities. A case study in central Arkansas demonstrates the application of these concepts and the effectiveness of the developed systems.

1. ROAD-TRAFFIC MONITORING AND ROUTING; STOCHASTIC ALGORITHMS FOR SAFETY AND EFFICIENCY By Adeyemi Fowe Masters Degree Thesis Defence Applied Science Department (Engineering Science and Systems) ‏ University of Arkansas at Little rock. Supervisor Dr. Yupo Chan Professor and Founding Chair Systems Engineering Department University of Arkansas at Little Rock.

2. The Transportation Problem Image from: http://www.railway-technology.com/projects/bangkok/bangkok3.html The demand on Infrastructure is on the increase, building more roads will not solve the problem. Hence the need for ITS (Intelligent Transportation Systems). It involves the application of Algorithms & Mathematical Models in describing and solving day-to-day transportation problems. One of the basic need of a driver on The road is Fastest Travel Time.

3. Thesis Outline Problem Description Thesis Contributions ATIS Data Arc Volume Estimation Using Spatial Relationship EM-BS Algorithm Case Study - Col-Glen Road Probability of Incident Risk non-FIFO Routing concept Hu and Chan Algorithm WSDOT Algorithm WSDOT_Risk Algorithm Case Study – Central Arkansas Mini TMC Live Demo Conclusion

4. ATIS ( Advanced Traveler Information System)

6. Thesis Outline Problem Description Thesis Contributions ATIS Data Arc Volume Estimation Using Spatial Relationship EM-BS Algorithm Case Study - Col-Glen Road Probability of Incident Risk non-FIFO Routing concept Hu and Chan Algorithm WSDOT Algorithm WSDOT_Risk Algorithm Case Study – Central Arkansas Mini TMC Live Demo Conclusion

7. Thesis Contributions A new non-FIFO routing algorithm ( WSDOT ) that search for possible wait-times (en-route) in a time-dependent transportation network is developed. (Fall 07) A mathematical model to compute Time-dependent Incident Probabilities from historical traffic and incident data. (Fall 08) An extension of WSDOT algorithm to WSDOT-R ( WSDOT-with-Risk ) algorithm which simultaneously minimizes a driver’s exposure to incident risk even as the fastest travel time is desired. (Summer 08) A mathematical algorithm to estimate traffic volumes in unknown arcs using partial information from upstream/downstream neighbors and entropy maximization. (Spring 09) Finally this thesis presents the application of all the models, their efficiency, and their performance on a real transportation network. Using the Highway Road of Central Arkansas as a case study, we design and present a prototype demo of a mini-TMC (Traffic Management Center). (Spring 08)

8. Thesis Outline Problem Description Thesis Contributions ATIS Data Arc Volume Estimation Using Spatial Relationship EM-BS Algorithm Case Study - Col-Glen Road Probability of Incident Risk non-FIFO Routing concept Hu and Chan Algorithm WSDOT Algorithm WSDOT_Risk Algorithm Case Study – Central Arkansas Mini TMC Live Demo Conclusion

9. Data Collection Systems Inductive Loop Sensors Traffic/Surveillance Cameras Aerial Photos CFVD (Cellular Floating Vehicle Data) Video Vehicle Detection Systems

10. Data is Key to a Functional ATIS Partial Information (incomplete Data) Perfect Information (Complete Data) Static/Persistent Data (Average & non-time dependent). Dynamic Data (Time Dependent) Real-Time Data (Streaming and Complete Time Dependent Data) Have Need

11. Thesis Outline Problem Description Thesis Contributions ATIS Data Arc Volume Estimation Using Spatial Relationship EM-BS Algorithm Case Study - Col-Glen Road Probability of Incident Risk non-FIFO Routing concept Hu and Chan Algorithm WSDOT Algorithm WSDOT_Risk Algorithm Case Study – Central Arkansas Mini TMC Live Demo Conclusion

12. Forecasting

13. Spatial Relationships In both spatial and temporal Dimensions; Closer by neighbors have tendency to be similar than farther away neighbors.

14. Arc Volume Estimation

15. Spatial Matrix First –Order Spatial Arc Neighbors

16. Spatial Matrix Second –Order Spatial Arc Neighbors

17. Spatial Weights

18. Spatial Weights

19. Model Formulation

20. Model Formulation

21. Model Formulation

22. Thesis Outline Problem Description Thesis Contributions ATIS Data Arc Volume Estimation Using Spatial Relationship EM-BS Algorithm Case Study - Col-Glen Road Probability of Incident Risk non-FIFO Routing concept Hu and Chan Algorithm WSDOT Algorithm WSDOT_Risk Algorithm Case Study – Central Arkansas Mini TMC Live Demo Conclusion

23. Arc Volume Estimate Naïve Solution

24. Entropy Maximization - Discrete

25. Entropy Maximization with Binary Search (EMBS)

26. Entropy Maximization with Binary Search (EMBS)

27. Entropy Maximization with Binary Search (EMBS)

28. Complexity Analysis

29. Thesis Outline Problem Description Thesis Contributions ATIS Data Arc Volume Estimation Using Spatial Relationship EM-BS Algorithm Case Study - Col-Glen Road Probability of Incident Risk non-FIFO Routing concept Hu and Chan Algorithm WSDOT Algorithm WSDOT_Risk Algorithm Case Study – Central Arkansas Mini TMC Live Demo Conclusion

35. Thesis Outline Problem Description Thesis Contributions ATIS Data Arc Volume Estimation Using Spatial Relationship EM-BS Algorithm Sample Computation Case Study - Col-Glen Road Probability of Incident Risk non-FIFO Routing concept Hu and Chan Algorithm WSDOT Algorithm WSDOT_Risk Algorithm Case Study – Central Arkansas Mini TMC Live Demo Conclusion

36. Time Dependent Incident Probability

37. Fundamental Diagram of Traffic Flow

38. Time Dependent Incident Probability – Peak vs Off-Peak

39. Poisson – Time Dependent Probability Model

40. Thesis Outline Problem Description Thesis Contributions ATIS Data Arc Volume Estimation Using Spatial Relationship EM-BS Algorithm Case Study - Col-Glen Road Probability of Incident Risk non-FIFO Routing concept Hu and Chan Algorithm WSDOT Algorithm WSDOT_Risk Algorithm Case Study – Central Arkansas Mini TMC Live Demo Conclusion

41. Key Terms Discrete vs Continuous representation of time A system is said to be discrete in time when the total time period T is divided into smaller periodic segments of time with integer increments. While a system is said to be continuous in time when point in the time space has a different value which can be represented by a floating decimal value of time. FIFO vs non-FIFO FIFO (First In First Out) represents a transportation network which follows; early departure  assured early arrival. While non-FIFO represents ; early departure  un-assured early arrival.

42. Non-FIFO Routing Concept

43. Key Questions... When is the best time to depart a particular node as you journey? Which is the optimal next hop node at that time? Which route is less prone to Incident risk ?

44. 3D View of Wait-time Set

45. Thesis Outline Problem Description Thesis Contributions ATIS Data Arc Volume Estimation Using Spatial Relationship EM-BS Algorithm Case Study - Col-Glen Road Probability of Incident Risk non-FIFO Routing concept Hu and Chan Algorithm WSDOT Algorithm WSDOT_Risk Algorithm Case Study – Central Arkansas Mini TMC Live Demo Conclusion

46. Chabini’s DOT (Decrease Order Of Time) Recursion Algorithm  denote the non-negative time required to travel from node j to node i  denote the total travel time associated with the current shortest path from node i to the destination node D at time t.  denote the sets of nodes directly connected to node D.

47. Stage Diagram; Wait time Search

48. Recursive Wait-time Search

49. Sequential Algorithm

50. WSDOT with Risk

51. Thesis Outline Problem Description Thesis Contributions ATIS Data Arc Volume Estimation Using Spatial Relationship EM-BS Algorithm Case Study - Col-Glen Road Probability of Incident Risk non-FIFO Routing concept Hu and Chan Algorithm WSDOT Algorithm WSDOT_Risk Algorithm Case Study – Central Arkansas Mini TMC Live Demo Conclusion

52. Network Graph

55. CFVD

56. Online Service; A mini-TMC

57. ITS metaLab miniTMC Demo http:// syseng.ualr.edu/metalab/research /

59. Conclusion Presented are new concepts that would help power a functional ATIS. We present a non-FIFO type algorithm WSDOT-Risk which would help drivers get faster travel time and simultaneously avoid incident risks en-route to their destination. We developed mathematical models to compute Incident risk as a function of time (either peak & off-peak or continuous). We also discussed the importance of real-time traffic information for an ATIS, should in case there is partial information, traffic information can be estimated in the spatial dimension using upstream and downstream relationship of network arcs. An extension to this could be in the temporal dimension, in which we can forecast some time into the future based on neighboring arcs.

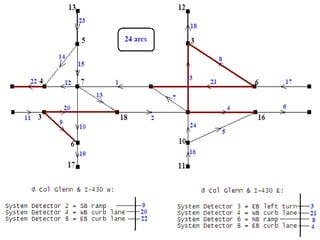
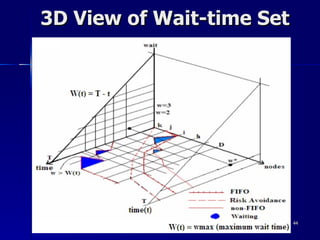
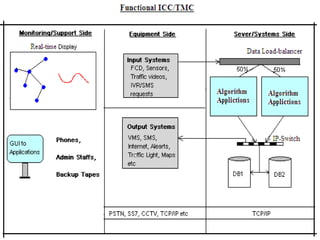
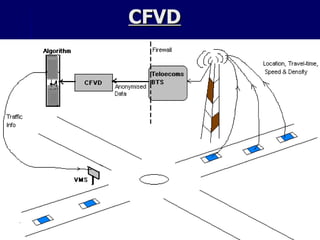
60. References [1] Dynamic Routing to Minimize Travel Time and Incident Risks (J.Hu and Y.Chan). [2] Chabini, I. A new shortest algorithm for discrete dynamic networks, Proceedings of the 8th IFAC Symposium on Transport System, China, Greece, Jun. 16-17, 1997, pp. 551-556 [3] Chabini, I. Discrete dynamic shortest path problems in transportation application: Complexity and algorithms with optimal run time, Transportation Research Record 1645, 1998, pp. 170-175. [4] Ziliaskopoulos, A. K. and Mahmassani, H. S. Design and implementation of a shortest path algorithm with time-dependent arc costs, Proceedings of 5 th advanced technology conference, Washington, D. C., 1992, pp. [5] Ziliaskopoulos, A. K. and Mahmassani, H. S. Time-dependent, shortest-path algorithm for real-time intelligent vehicle highway system applications, Transportation Research Record 1408, 1993, pp 94-100. [6] Chan, Y. Location Transport and Land-Use: Modeling Spatial-Temporal Information. Springer, Berlin – New York, 2005, pp. 506. [7] Farradyne, P. B. et al. Arkansas Statewide Intelligent Transportation Systems (ITS) Strategic Plan, Prepared for Arkansas State Highway & Transportation Department, 2002. [8] Metroplan. Intelligent Transportation System, Central Arkansas Regional Transportation Study, June, 2002. [9] Bellman, R. On a routing problem. Quart. Appl. Mathematics, Vol. 16, 1958, pp. 87-90.