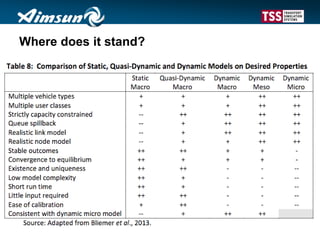
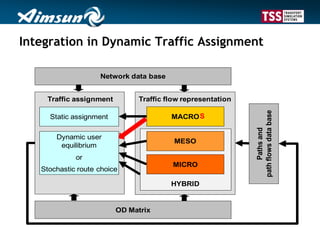
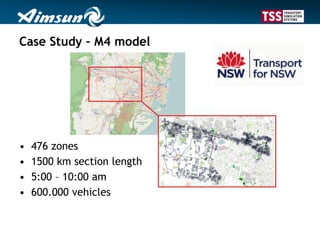
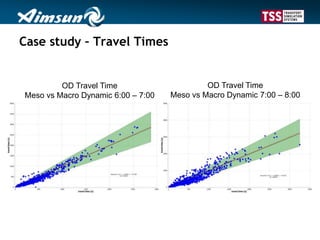
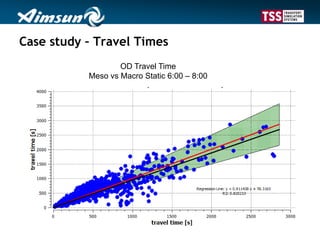
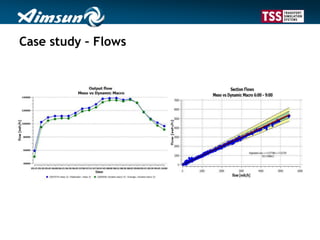
This document describes a dynamic macroscopic traffic model integrated into dynamic traffic assignment. The model uses continuous flow equations to model traffic flow on links between nodes. Nodes route traffic according to conservation and maximization principles. The model is calibrated using a case study network with over 500 zones, showing travel times comparable to a mesoscopic model but with faster computation. While coarse, the dynamic macroscopic model provides an efficient alternative for large-scale dynamic traffic assignment problems.

1. A Dynamic Macroscopic model integrated into Dynamic
Traffic Assignment: advantages and disadvantages
Martijn Breen & Jordi Casas

2. Overview
• Motivation
• Model description
• Isolated examples
• Case study
• Conclusion

3. Motivation
• Travel Demand models require O/D travel times
• Current static models do not capture congestion/queues
spillback
• Vehicle-based dynamic models are more complex

4. Where does it stand?

5. Model – Link model
• Continuous flow model
• Conservation equation:
dρ
dt
+
dq
dx
= 0
• Flux rate function:
q = ϕ ρ

6. Model – link model (ii)
Forward Wave Backward Wave
U t −
L
γ
= V t U t − V t −
L
ω
= KL
Mark P.H. Raadsen, Michiel C.J. Bliemer, Michael G.H. Bell, An efficient and exact event-based algorithm for solving simplified first order dynamic
network loading problems in continuous time

7. Node model
• Generic
• Maximizing flows w.r.t
constraints.
• Conservation of turn
fractions
• Invariance principle.
Tampère C.M.J., Corthout R., Cattrysse D., Immers, L.H. (2011). A Generic Class of First Order Node Models for Dynamic Macroscopic
Simulation of Traffic Flows. Transportation Research Part B: methodological. Volume 45B issue 1, 2011, pp289-309

8. Path propagation (integration with DTA)

9. MACRO
MESO
MICRO
Static assignment
Dynamic user
equilibrium
or
Stochastic route choice
OD Matrix
Network data base
Pathsand
pathflowsdatabase
Traffic flow representationTraffic assignment
HYBRID
Integration in Dynamic Traffic Assignment
S

10. Network input / calibration parameters
• Geometry
• Section
– Free flow speed
– Capacity
– Jam density
• Turn
– Capacity
• Traffic lights control plan

11. Isolated examples - spillback

12. Isolated examples – traffic lights

13. Isolated examples – Give-way node

14. Case Study – M4 model
• 476 zones
• 1500 km section length
• 5:00 – 10:00 am
• 600.000 vehicles

15. Case study – Travel Times
OD Travel Time
Meso vs Macro Dynamic 6:00 – 7:00
OD Travel Time
Meso vs Macro Dynamic 7:00 – 8:00

16. Case study – Travel Times
OD Travel Time
Meso vs Macro Static 6:00 – 8:00

17. Case study – Flows

18. Computational performance
Simulator Link actualization
threshold [%]
Network Loading
[seconds]
Mesoscopic n/a 362
Macro dynamic 5 144
Macro dynamic 10 133
Macro dynamic 20 123

19. Density view mode

20. Conclusions
• Dynamic Macroscopic model integrated in Dynamic
Traffic Assignment
• Travel times comparable under free flow and congested
situations
• O/D travel times are more sensitive to errors for coarse
(higher threshold) simulation
• Dynamic Macroscopic model is easily calibrated due to
few calibration parameters
• Dynamic Macroscopic doesn’t replace the Mesoscopic

21. Future developments
• Improve traffic signal treatment
• Improve computation speed
• Add actions like:
– Metering
– Force turn
– Capacity reduction