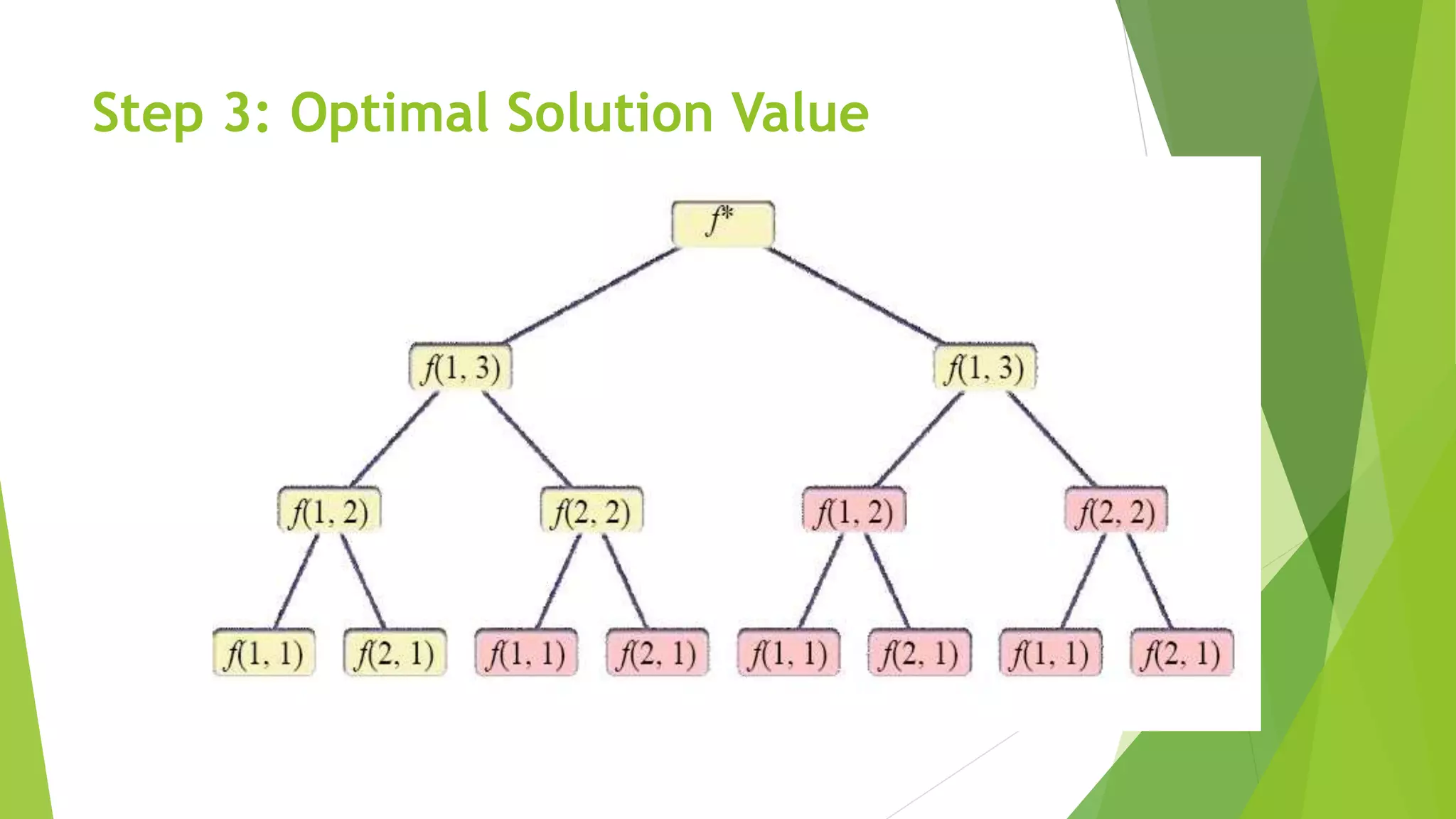
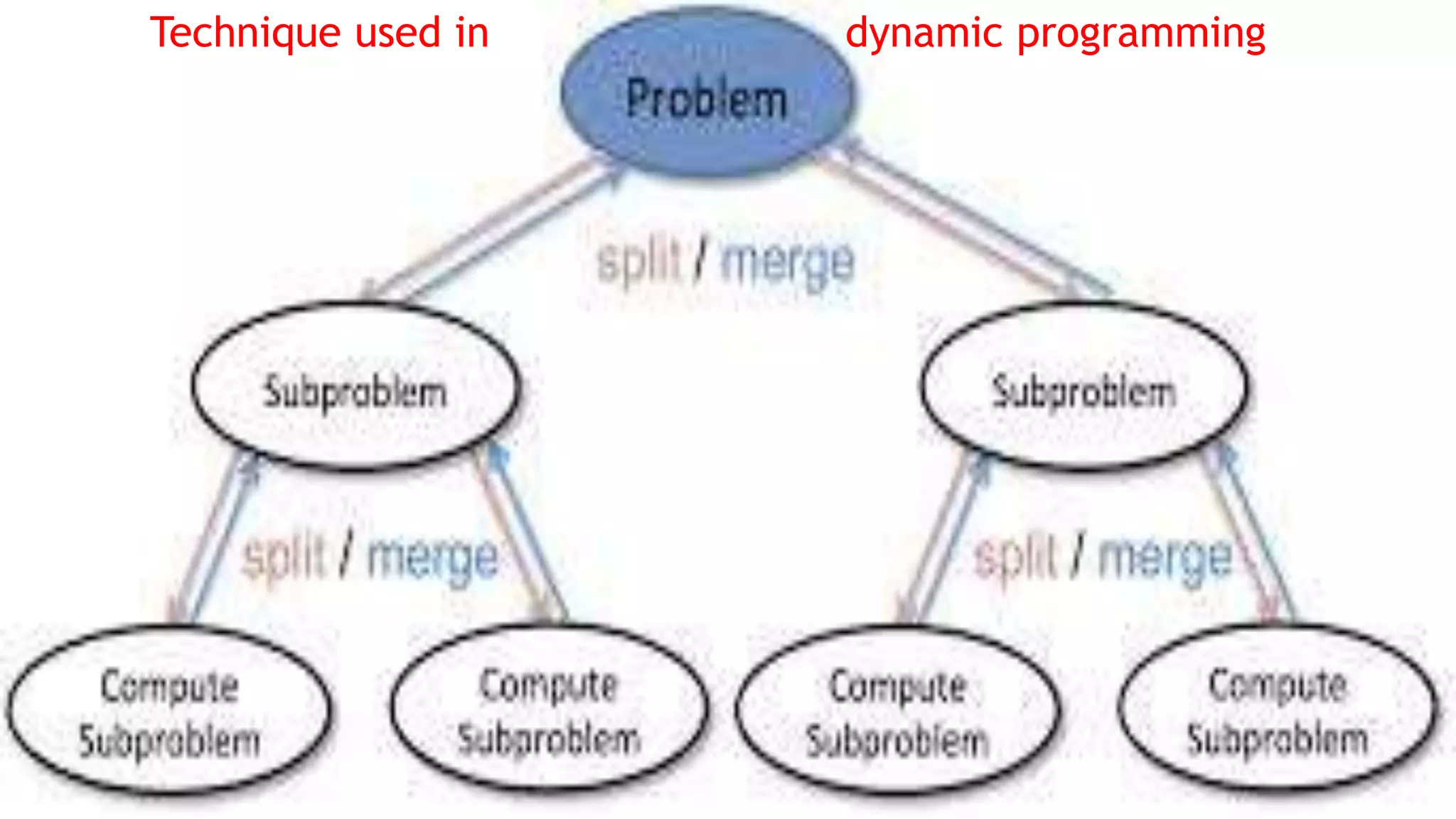
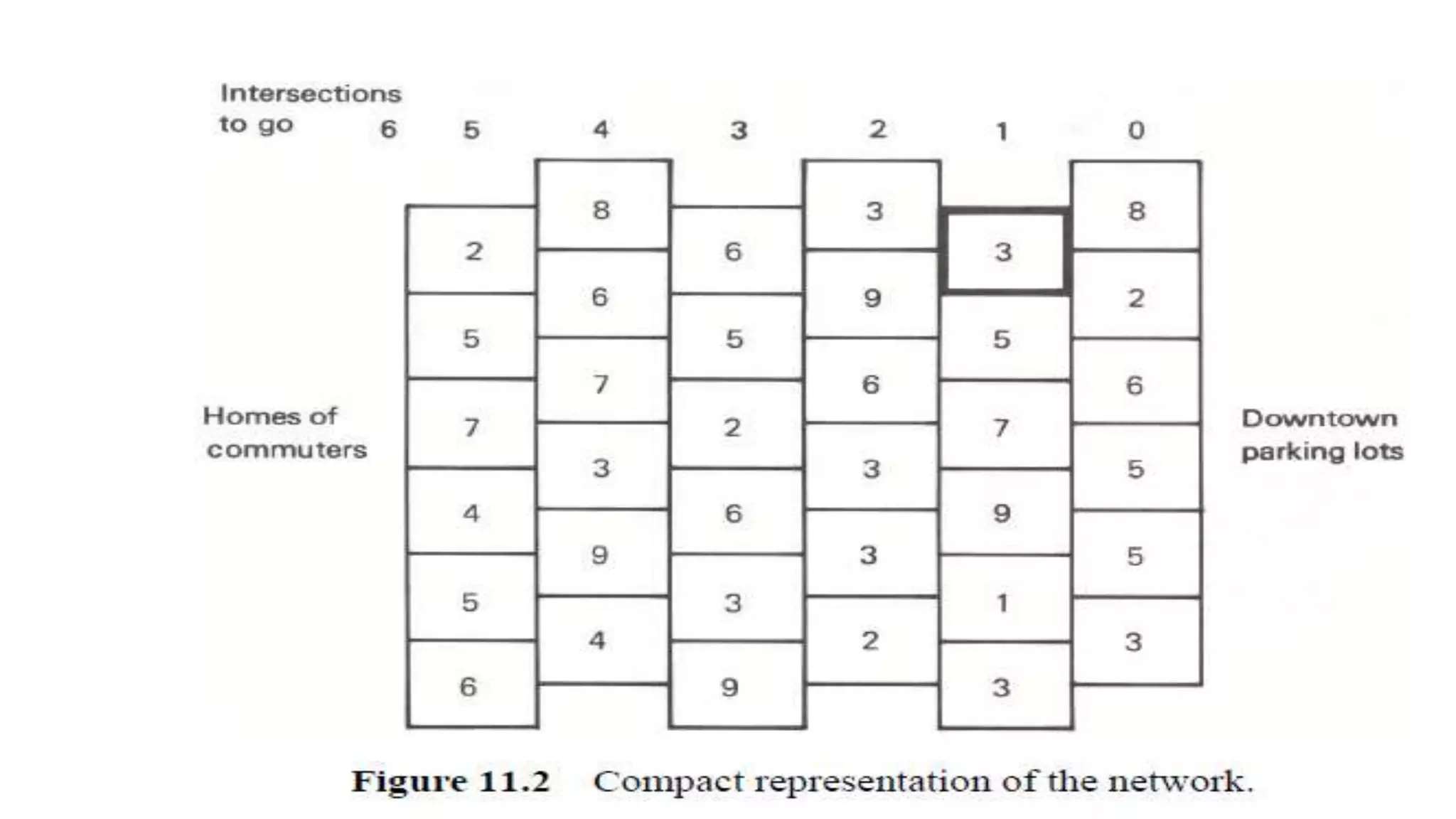
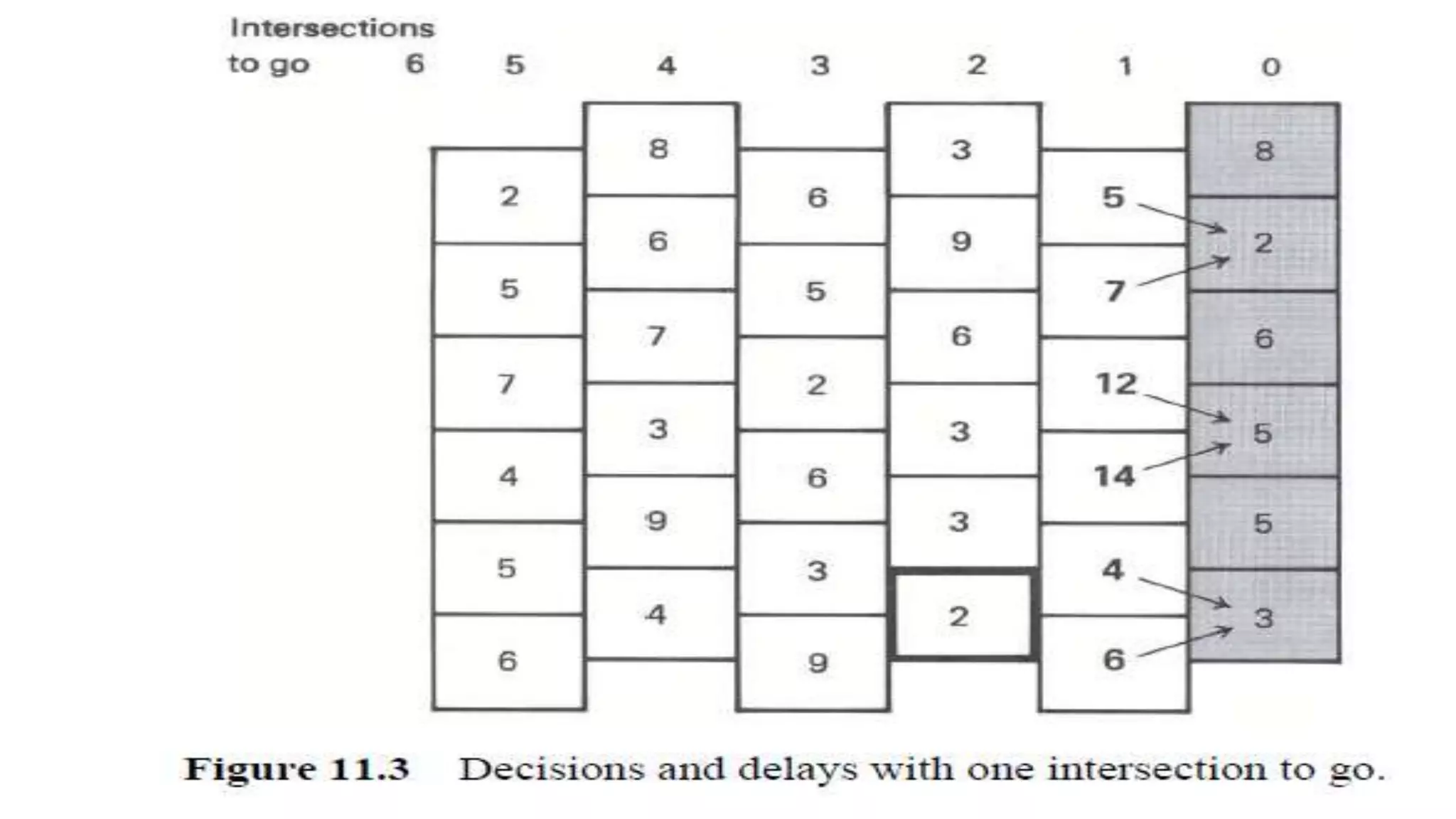
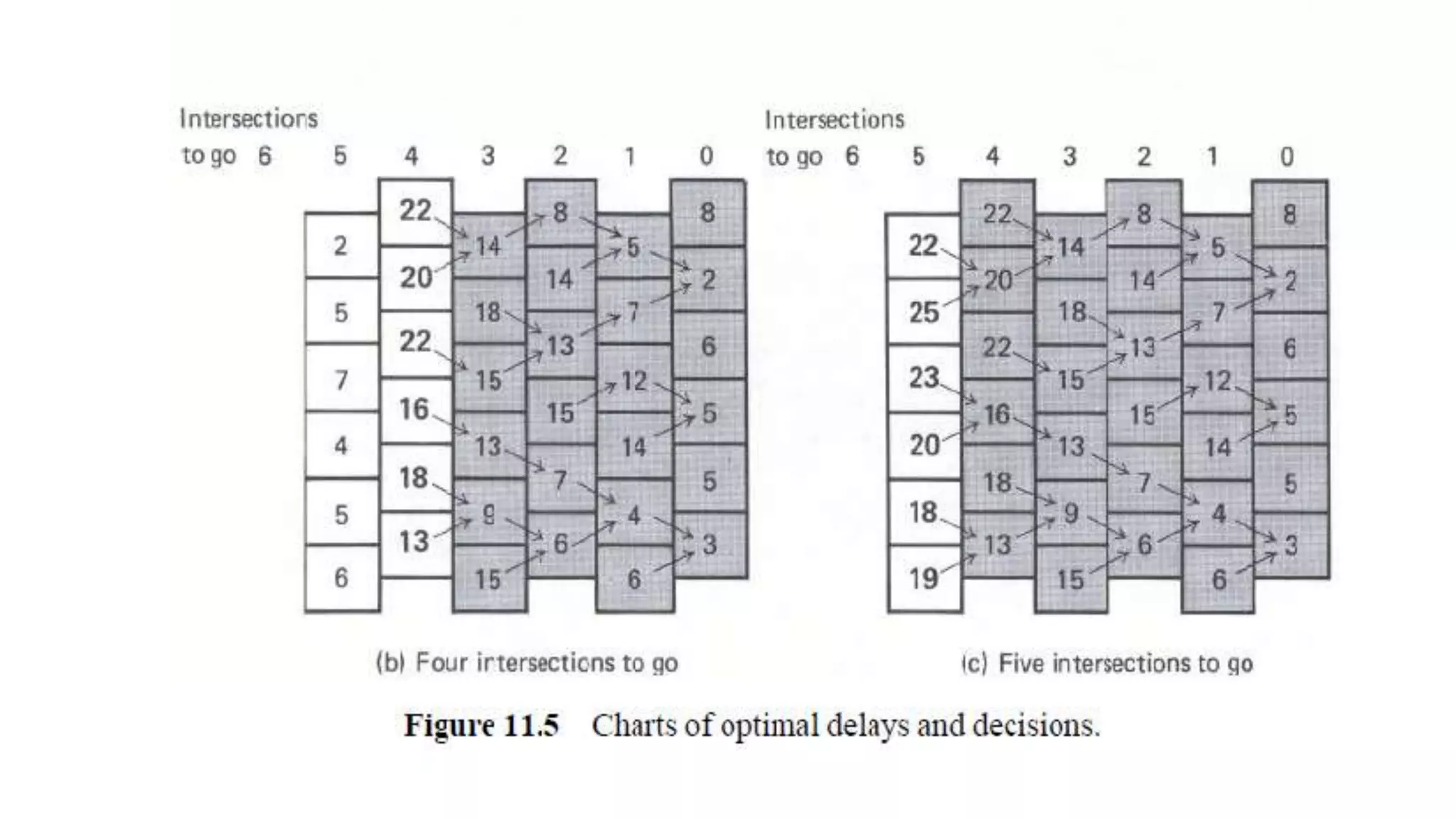
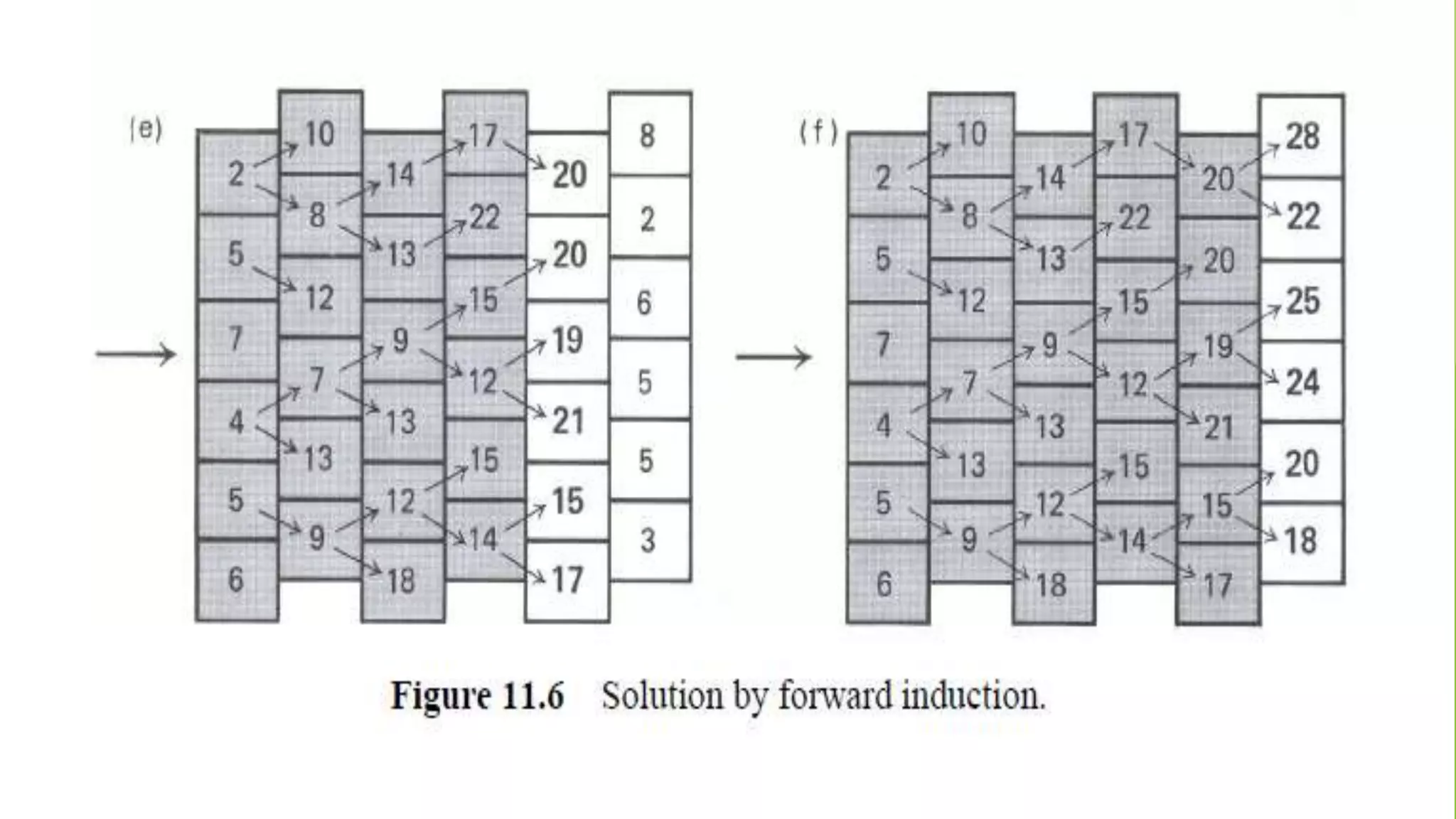
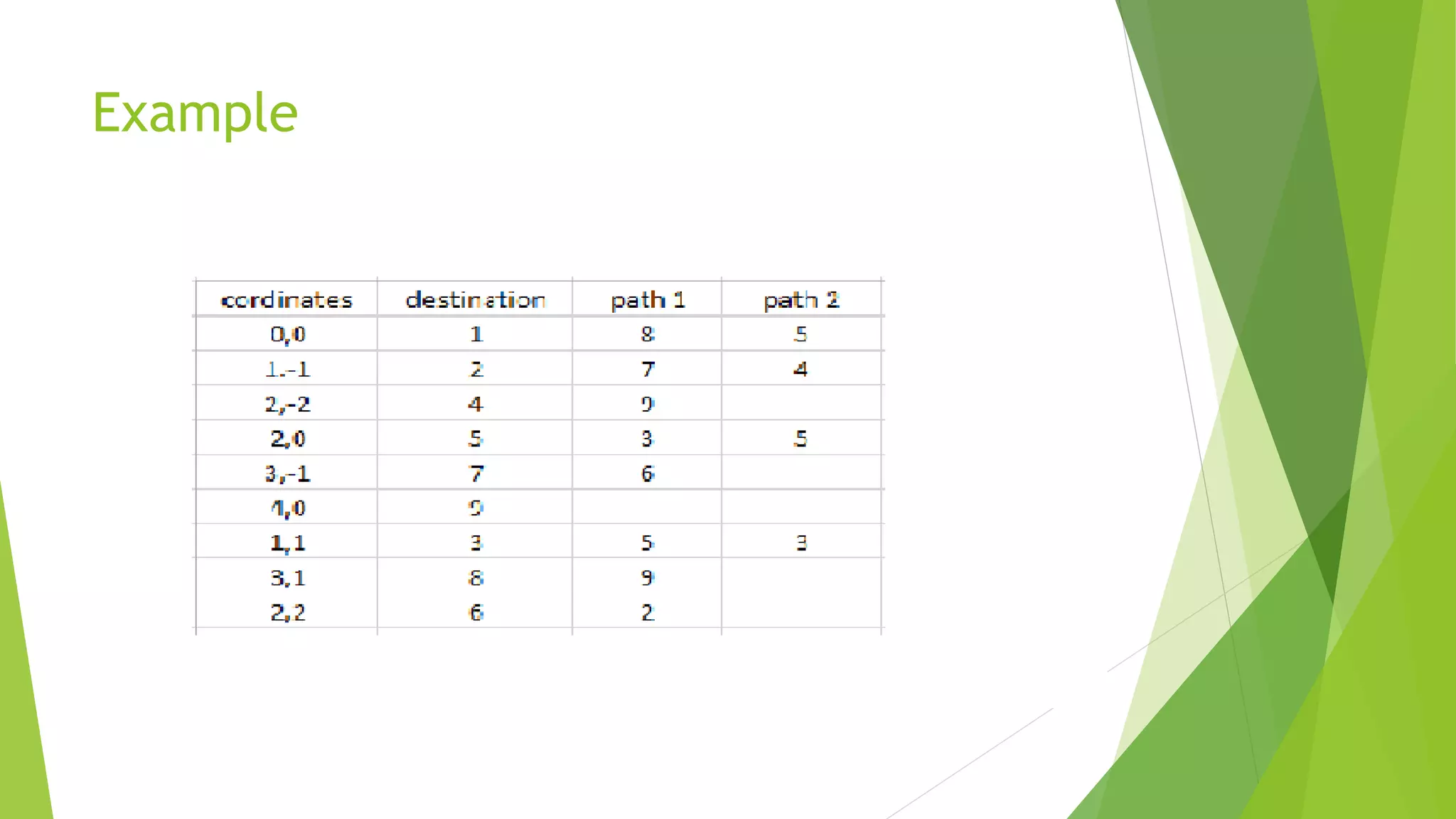
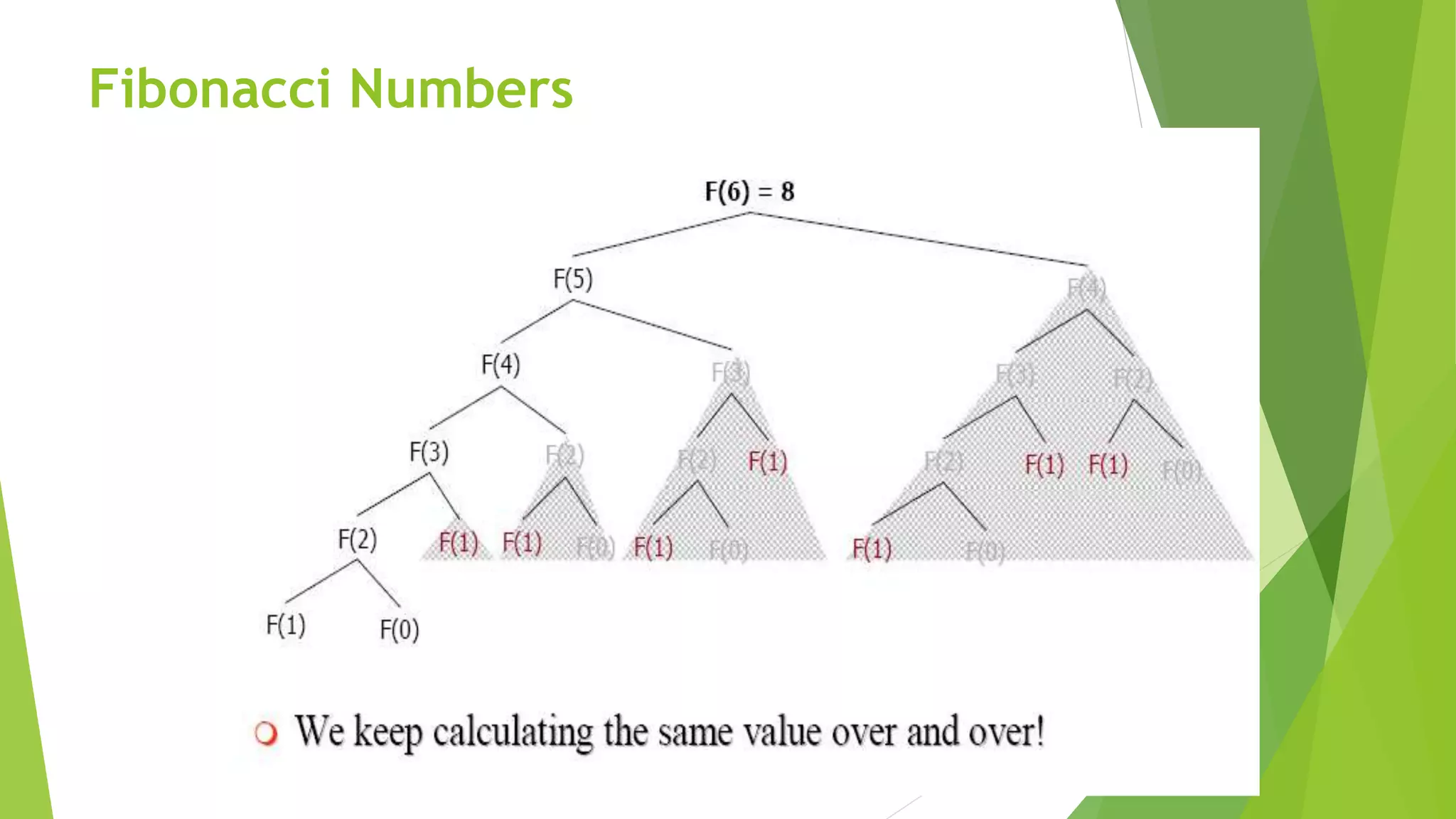
The document discusses dynamic programming, including its meaning, definition, uses, techniques, and examples. Dynamic programming refers to breaking large problems down into smaller subproblems, solving each subproblem only once, and storing the results for future use. This avoids recomputing the same subproblems repeatedly. Examples covered include matrix chain multiplication, the Fibonacci sequence, and optimal substructure. The document provides details on formulating and solving dynamic programming problems through recursive definitions and storing results in tables.

1. Start with the name of ALLAH the
Most merciful and the most
beneficial

2. Dynamic Programming
Prepared by :-

3. Contents:
 Meaning
 Defination
 What is dynamic programming used for
 Technique used in it
 Divide and Conquer Strategy
 General Divide and Conquer recurrence
 Common example
 Approaches of dynamic programming
 Elements of Dynamic Programming
 Dynamic Programming and Chain Matrix Multiplication
 Fibonacci Numbers
 Steps for problem solving
 Advantages and Disadvantages
 Good bye :p :p

4. What does Dynamic Mean ??

5. Characterized by continuous change activity
Characterized by much activity and vigor, especially
in bringing about change energetic and forceful

7. The designing, scheduling, or planning of a program
Ref http://www.thefreedictionary.com

8. So Combine Meaning Of Dynamic Programming is :
Change and Schedule a Solution for a problem

9. Defination :
 Dynamic Programming refers to a
very large class of algorithms. The
idea is to break a large problem
down (if possible) into incremental
steps so that, at any given stage,
optimal solutions are known to sub-
problems.
Ref :- Monash University
DEFINATION :

10. Use of dynamic programming
 Dynamic programming is used for problems requiring a sequence of interrelated
decision. This means that to take another decision we have to depend on the
previous decision or solution formed.

11. Technique used in dynamic programming

13. The Divide and Conquer Algorithm
• Divide_Conquer(problem P)
• {
• if Small(P) return S(P);
• else {
• divide P into smaller instances P1, P2, …, P k , k1;
• Apply Divide_Conquer to each of these sub problems;
• return Combine(Divide_Conquer(P1),
Divide_Conquer(P2),…, Divide Conquer(P k));
• }
• }

14. Divide Conquer recurrence relation
 The computing time of Divide Conquer is
 T(n) is the time for Divide Conquer on any input size n.
 g(n) is the time to compute the answer directly (for small inputs)
 f(n) is the time for dividing P and combining the solutions.
14





)()(...)()(
)(
)(
21 nfnTnTnT
ng
nT
k
n small
otherwise

15. 15
General Divide and Conquer recurrence
The Master Theorem
T(n) = aT(n/b) + f (n), where f (n) ∈ Θ(n k)
1. a < bk T(n) ∈ Θ(n k)
2. a = bk T(n) ∈ Θ(n k lg n )
3. a > bk T(n) ∈ Θ(n log b a)
the time spent on solving a sub problem of size n/b.
the time spent on dividing the problem
into smaller ones and combining their solutions.

16. Difference between DP and Divide-and-
Conquer
 Using Divide-and-Conquer to solve these problems is inefficient because
the same common sub problems have to be solved many times.
 DP will solve each of them once and their answers are stored in a table
for future use.

25. i) Backward Recursion
ii) Forward Recursion
Two Approach of Dynamic Programming

27. It Contains Sequence of “n” decisions.
Each “n” corresponding to one of the decision.
Each stage of analysis is described by a set of elements
decision, input state, output state and return.
Then symbolic representation of n stages of analysis using
backward recursion so we can formalize the notation
Backward recursion
Cumulative return = Direct return + Cumulative return
through stage from stage through stage i-1

28.  We use sb to denote the previous state
 Tb determines the state that came before s when the decision made to reach state s is d
 Db(s) is the set of decisions that can be used to enter state s
sb = Tb(s, d), //where d belongs to Db(s)
Backward recursion formula

30.  Approach takes a problem
 Decomposed into a sequence of n stages
 Analyzes the problem starting with the first stage
in the sequence
 Working forward to the last stage
 it is also known as deterministic probability
approach
Forward recursion

31. Example

33. Elements of Dynamic Programming
i) Optimal substructure
ii) Overlapping sub problem
iii) Memoization

34.  a problem is said to have optimal substructure if an optimal solution can be
constructed efficiently from optimal solutions of its sub problems. This property is
used to determine the usefulness of dynamic programming
ref : wikipedia

36. Optimal Substructure
 This is the necessary property , if this property is not present we cant use
dynamic programming.
 a problem p , with sub problems p1,p2.
Solution of problem p is s , and s1 is the optimum solution of sub problem p1,and
s2 is the optimum solution of sub problem p2.
 Claim “s” is the optimal solution ,if both solution of the sub problems are
optimal only then the final solution is optimal.

41. Dynamic
Programming
Chain
Matrix
Multiplication

42. Dynamic Programming and
Chain Matrix Multiplication
In mathematics or computer science, Dynamic
Programming is a method for solving complex problems
by breaking them down into simpler sub-problems. So,
Matrix chain multiplication is an ideal example that
demonstrates utility of dynamic programming.
Engineering applications often have to multiply a large
chain of matrices with large dimensions, for example: 100
matrices of dimension 100×100. We can multiply this chain
of matrices in many different ways, but we will go for that
way which takes lower computations.

43. Dynamic Programming of Chain Matrix
Multiplication
For example, we are going to multiply 4 matrices:
M1 = 2 x 3
M2 = 3 x 4
M3 = 4 x 5
M4 = 5 x 7
And we have conditions for multiplying matrices:
• We can multiply only two matrices at a time.
• When we go to multiply 2 matrices, the number of columns of 1st matrix should
be same as the number of rows of 2nd matrix.

44. M1 = 2 x 3
M2 = 3 x 4
M3 = 4 x 5
M4 = 5 x 7
( M1 M2 )( M3 M4 ) = 220
(( M1 M2 ) M3 ) M4 = 134
M1 ( M2 ( M3 M4 ) = 266
( M1 ( M2 M3 ) M4 = 160
M1 (( M2 M3 ) M4 ) = 207
We can multiply the chain of matrices by following those
conditions in these ways:
Numbers of the rightmost side is number of total scalar
multiplication. So we have realized that we can reduce
the number of total multiplication and this reduced
time is a fact for a large chain of matrices.

45. Algorithm and Mechanism
Renaming matrices as Mi and dimensions as Pi - 1 x Pi , we have got:
M1 = P0 x P1
M2 = P1 x P2
M3 = P2 x P3
M4 = P3 x P4
| | |
Mi = Pi – 1 x Pi

46. We will use a formula:
Where C i, j means Mi to Mj .
i.e.: C 1, 4 means M1 to M4 .
And we will use a variable 'k' as follows:
M1 |k=1 M2 M3 M4
M1 M2 |k=2 M3 M4
M1 M2 M3 |k=3 M4

47. The thing we’re going to do is to apply above formula for every 'k' in the range 'i' to
'j' and pick the lowest value every step.
C 1 , 4 = min ( C1 , 1 + C2 , 4 + P0 * P1 * P4 , C1 , 2 + C3 , 4 + P0 * P2 * P4 , C1 , 3 + C4 , 4 + P0 *
P3 * P4 ) = min ( 207, 220, 134 ) = 134
C 2, 4 = min ( C2 , 2 + C3 , 4 + P1 * P2 * P4 , C2 , 3 + C4 , 4 + P1 * P3 * P4 ) = min ( 224, 165 )
= 165
C 1, 3 = min ( C1 , 1 + C2 , 3 + P0 * P1 * P3 , C1 , 2 + C3 , 3 + P0 * P2 * P3 ) = min ( 90, 64 ) =
64
C 1, 2 = P0 * P1 * P2 = 24
C 2, 3 = P1 * P2 * P3 = 60
C 3, 4 = P2 * P3 * P4 = 140

48. Pseudocode
1. int Chain( int i, int j )
2. {
3. int min = 10000, value, k;
4. if( i == j ){
5. return 0;
6. }
7. else{
8. for( k = i; k < j; k++ ){
9. value = (Chain(i, k) + Chain(k + 1, j) + (dimensions[i-1] *
dimensions[k] * dimensions[j]));
10. if( min > value ){
11. min = value;
12. mat[i][j] = k;
13. }
14. }
15. }
16. return min;

49. 1. int main(void)
2. {
3. int result, i;
4. printf("Enter number of matrices: ");
5. scanf("%d", &n);
6. printf("Enter dimensions : ");
7. for( i = 0; i <= n; i++ ){
8. scanf("%d", &dimensions[i]);
9. }
10. result = Chain(1, n);
11. printf("nTotal number of multiplications: %d andn", result);
12. printf("Multiplication order is: ");
13. PrintOrder( 1, n );
14. printf("n");
15. }

50. Input and Output in Console App

51. Fibonacci Numbers

52. Fibonacci Numbers
 Fn= Fn-1+ Fn-2 n ≥ 2
 F0 =0, F1 =1
 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
 Straightforward recursive procedure is slow!
 Let’s draw the recursion tree

53. Fibonacci Numbers

54. Fibonacci Numbers
 How many summations are there? Using Golden Ratio
 As you go farther and farther to the right in this sequence, the ratio of a term to the one
before it will get closer and closer to the Golden Ratio.
 Our recursion tree has only 0s and 1s as leaves, thus we have 1.6n summations
 Running time is exponential!

55. Fibonacci Numbers
 We can calculate Fn in linear time by remembering solutions to the solved
subproblems – dynamic programming
 Compute solution in a bottom-up fashion
 In this case, only two values need to be remembered at any time

57. Steps for problem solving
 There are four steps of problem solving
 Optimal Solution Structure
 Recursive Solution
 Optimal Solution Value
 Optimal Solution

58. Problem Definition
 Problem: Given all these costs, what stations should be chosen from line 1
and from line 2 for minimizing the total time for car assembly.
 “Brute force” is to try all possibilities.
 requires to examine Omega(2n) possibilities
 Trying all 2n subsets is infeasible when n is large.
 Simple example : 2 station  (2n) possibilities =4
start end

59. Step 1: Optimal Solution Structure
optimal substructure : choosing the best path to Sij.
 The structure of the fastest way through the factory (from
the starting point)
 The fastest possible way to get through Si,1 (i = 1, 2)
 Only one way: from entry starting point to Si,1
 take time is entry time (ei)

60. Step 1: Optimal Solution Structure
 The fastest possible way to get through Si,j (i = 1, 2) (j = 2, 3, ..., n).
Two choices:
 Stay in the same line: Si,j-1  Si,j
 Time is Ti,j-1 + ai,j
 If the fastest way through Si,j is through Si,j-1, it must have taken a fastest way through Si,j-1
 Transfer to other line: S3-i,j-1  Si,j
 Time is T3-i,j-1 + t3-i,j-1 + ai,j
 Same as above

61. Step 1: Optimal Solution Structure
 An optimal solution to a problem
 finding the fastest way to get through Si,j
 contains within it an optimal solution to sub-problems
 finding the fastest way to get through either Si,j-1 or S3-i,j-1
 Fastest way from starting point to Si,j is either:
 The fastest way from starting point to Si,j-1 and then directly from Si,j-1 to
Si,j
or
 The fastest way from starting point to S3-i,j-1 then a transfer from line 3-i to
line i and finally to Si,j
 Optimal Substructure.

62. Example

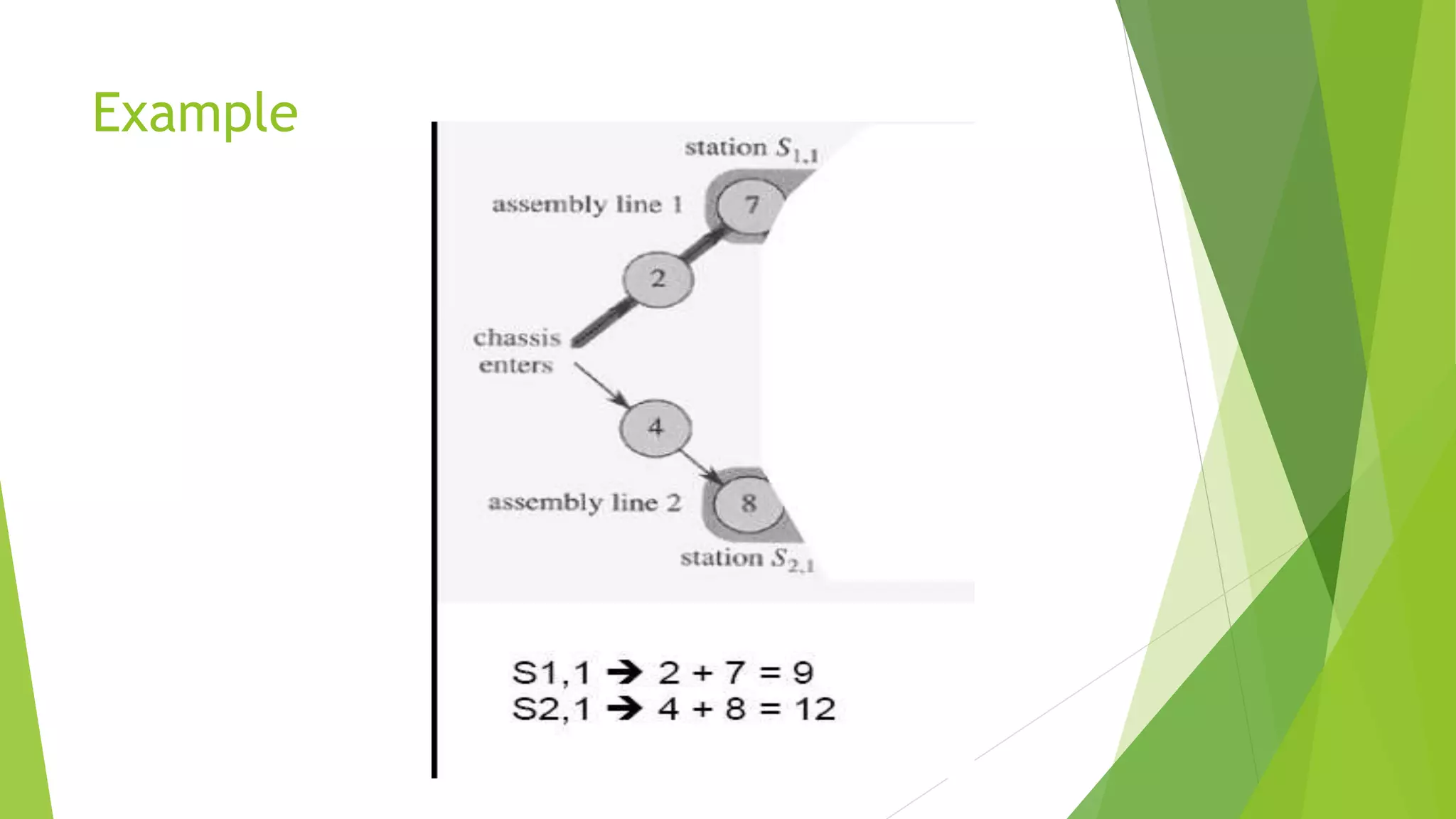
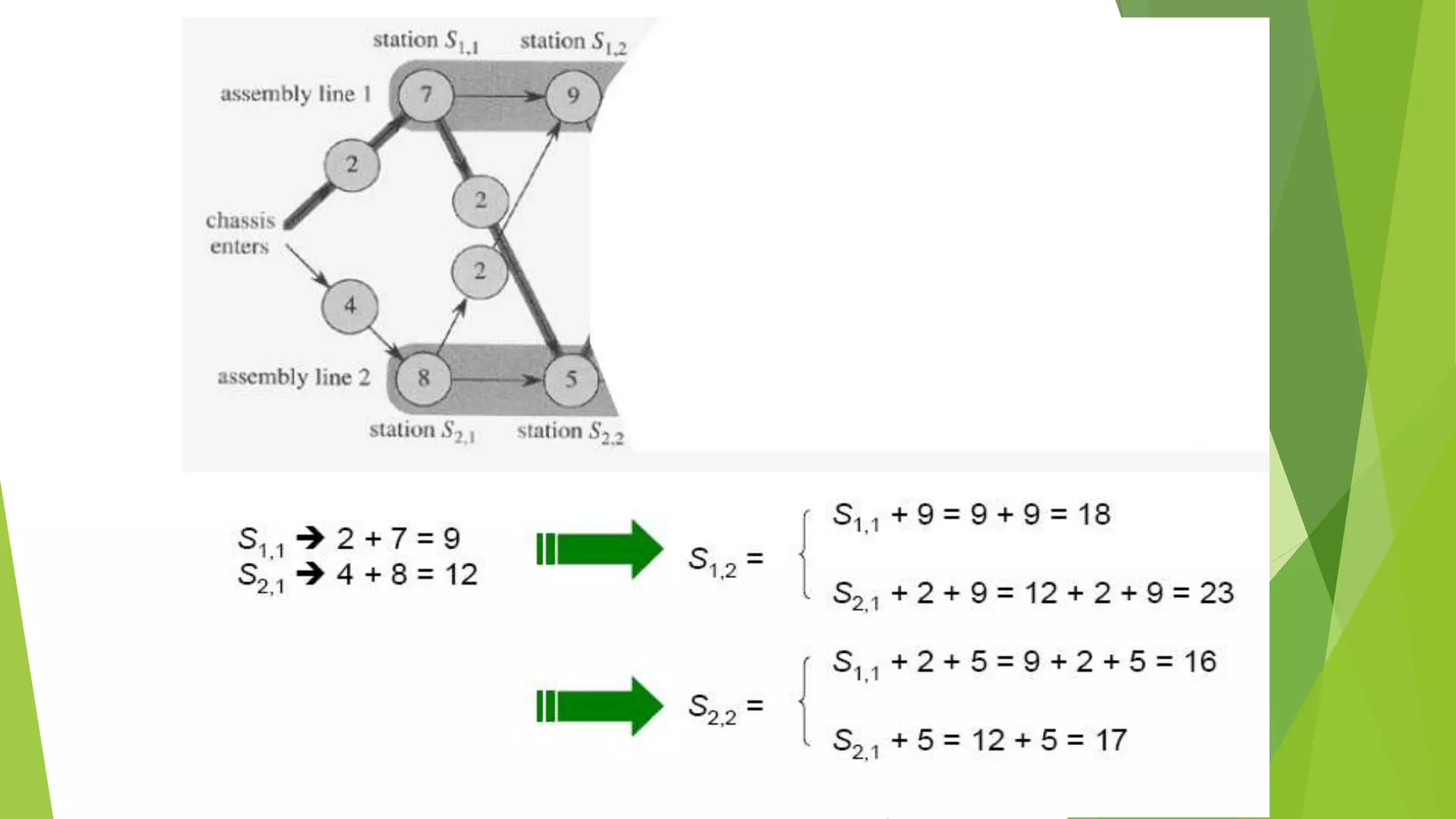
65. Step 2: Recursive Solution
 Define the value of an optimal solution recursively in terms of the
optimal solution to sub-problems
 Sub-problem here
 finding the fastest way through station j on both lines (i=1,2)
 Let fi [j] be the fastest possible time to go from starting point through Si,j
 The fastest time to go all the way through the factory: f*
 x1 and x2 are the exit times from lines 1 and 2, respectively

66. Step 2: Recursive Solution
 The fastest time to go through Si,j
 e1 and e2 are the entry times for lines 1 and 2

67. Example

68. Example

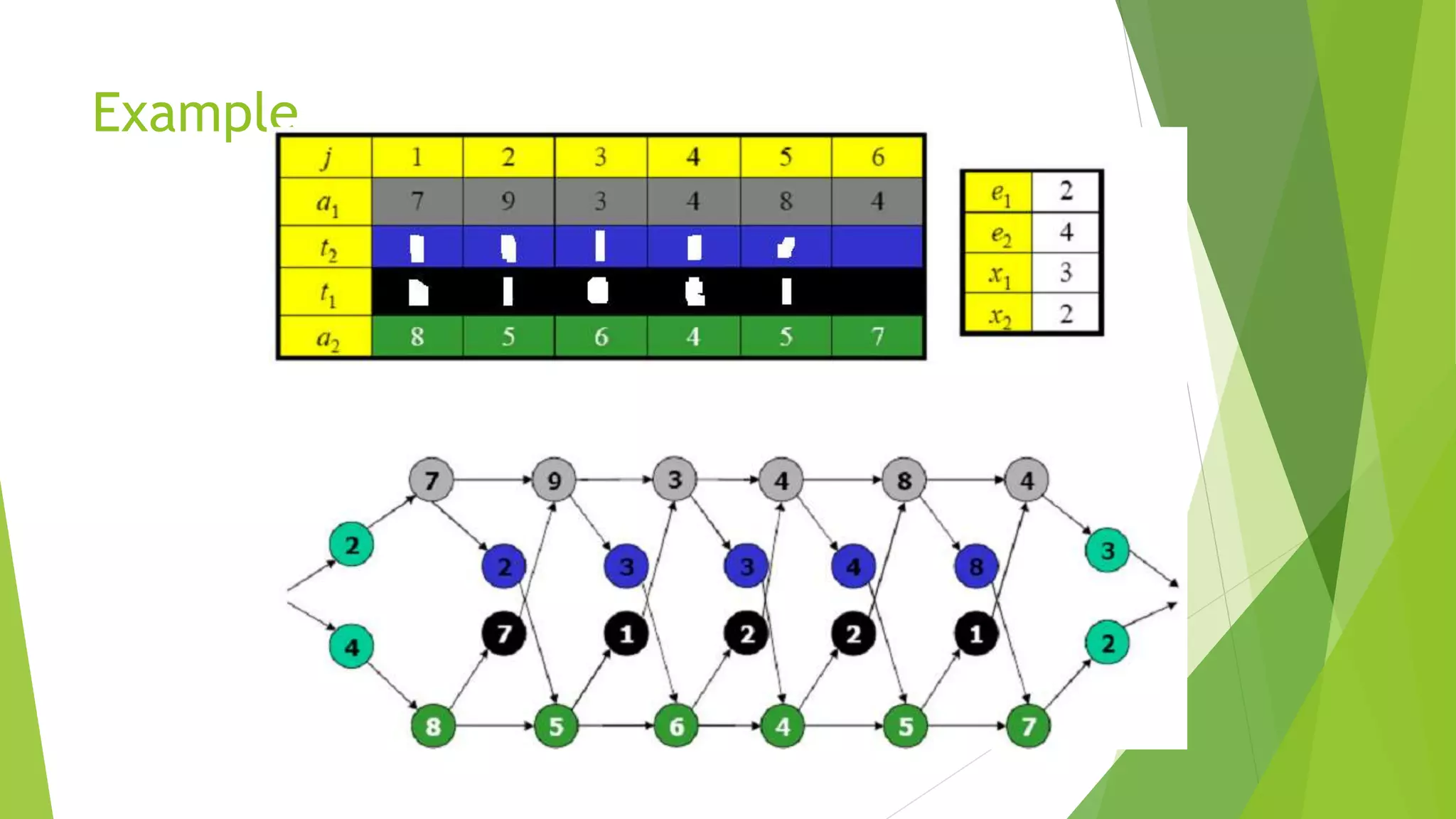
69. Step 2: Recursive Solution
 To help us keep track of how to construct an optimal solution, let us define
 li[j ]: line # whose station j-1 is used in a fastest way through Si,j (i = 1, 2, and j =
2, 3,..., n)
 we avoid defining li[1] because no station precedes station 1 on either lines.
 We also define
 l*: the line whose station n is used in a fastest way through the entire factory

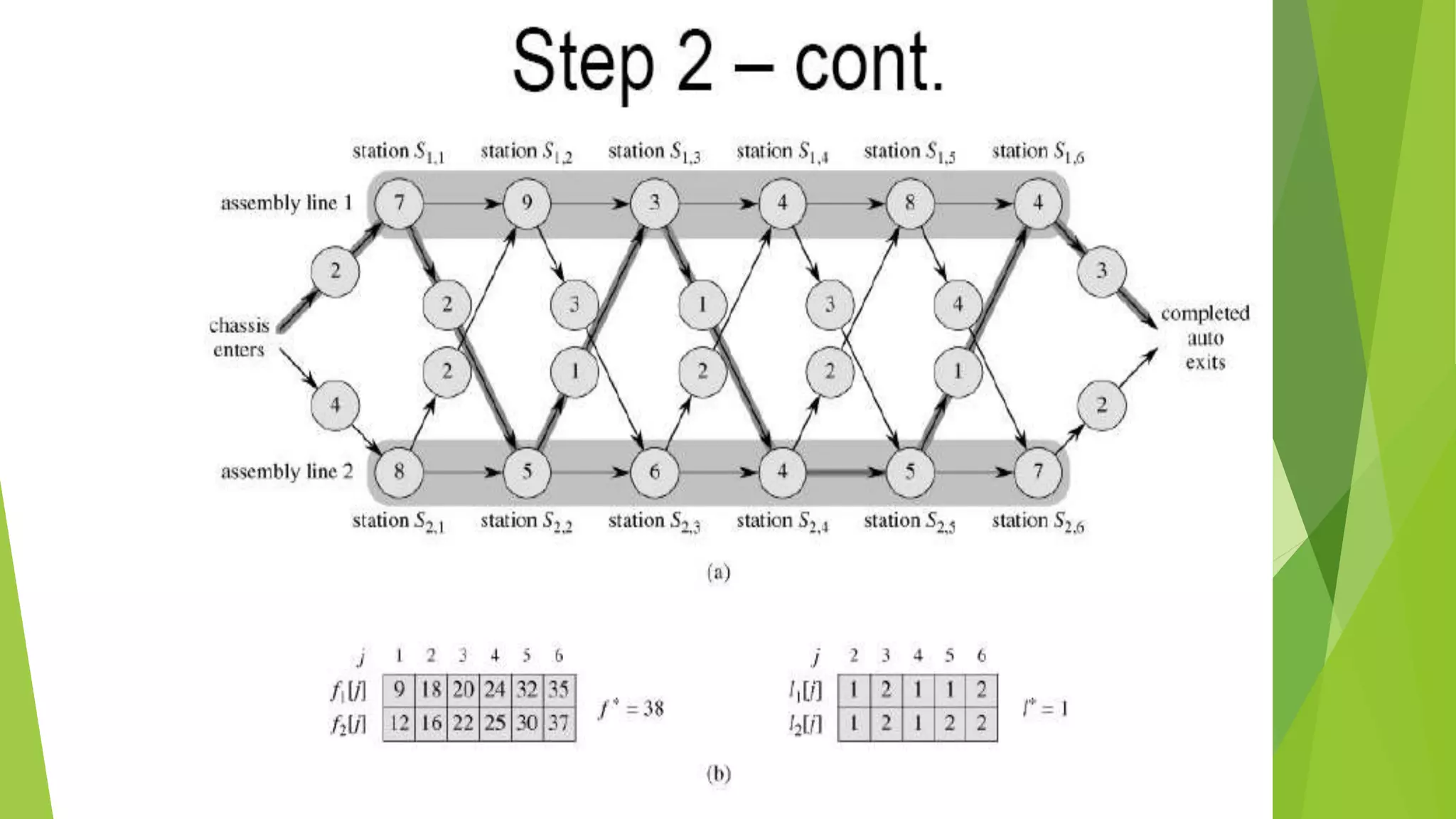
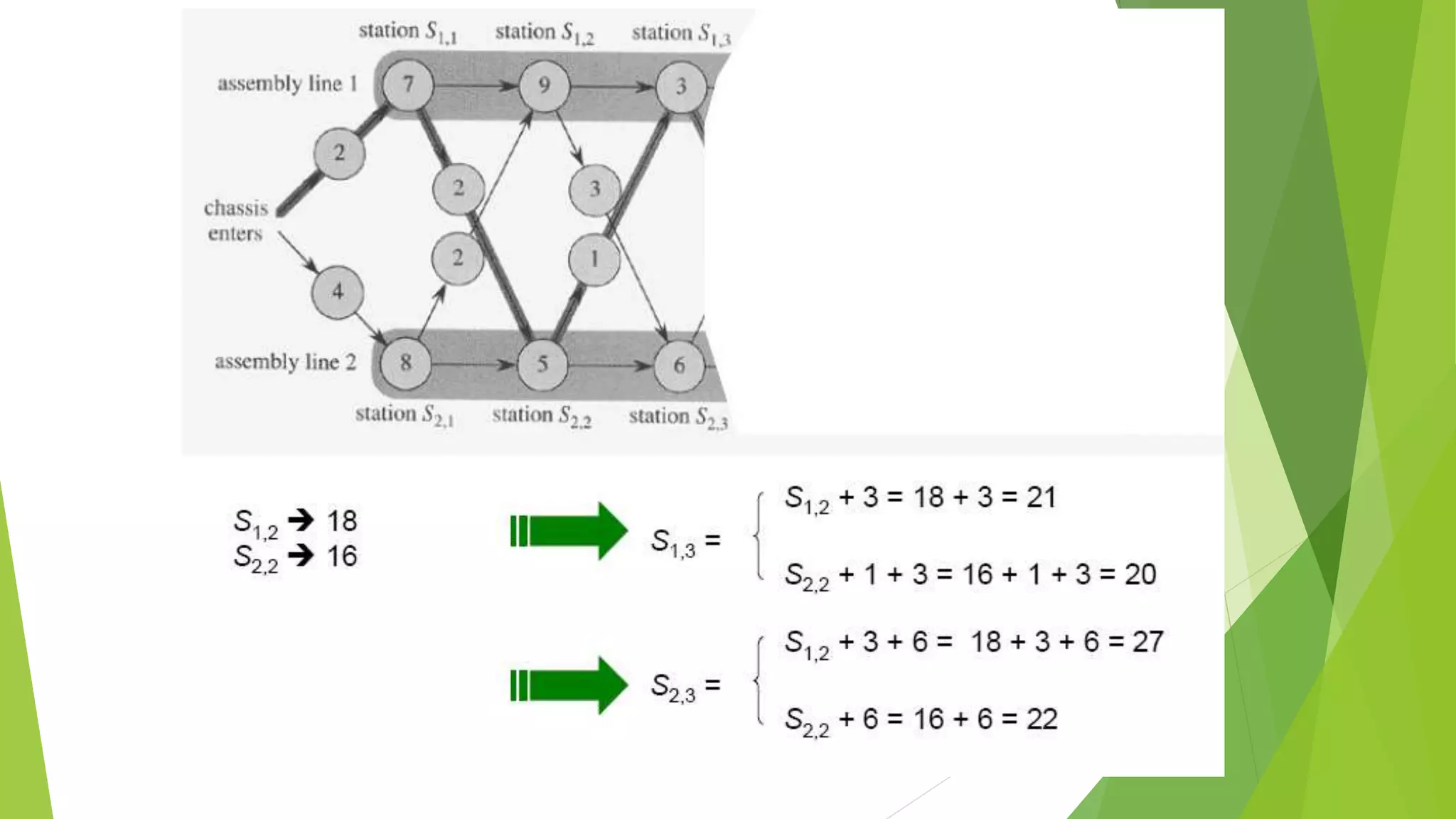
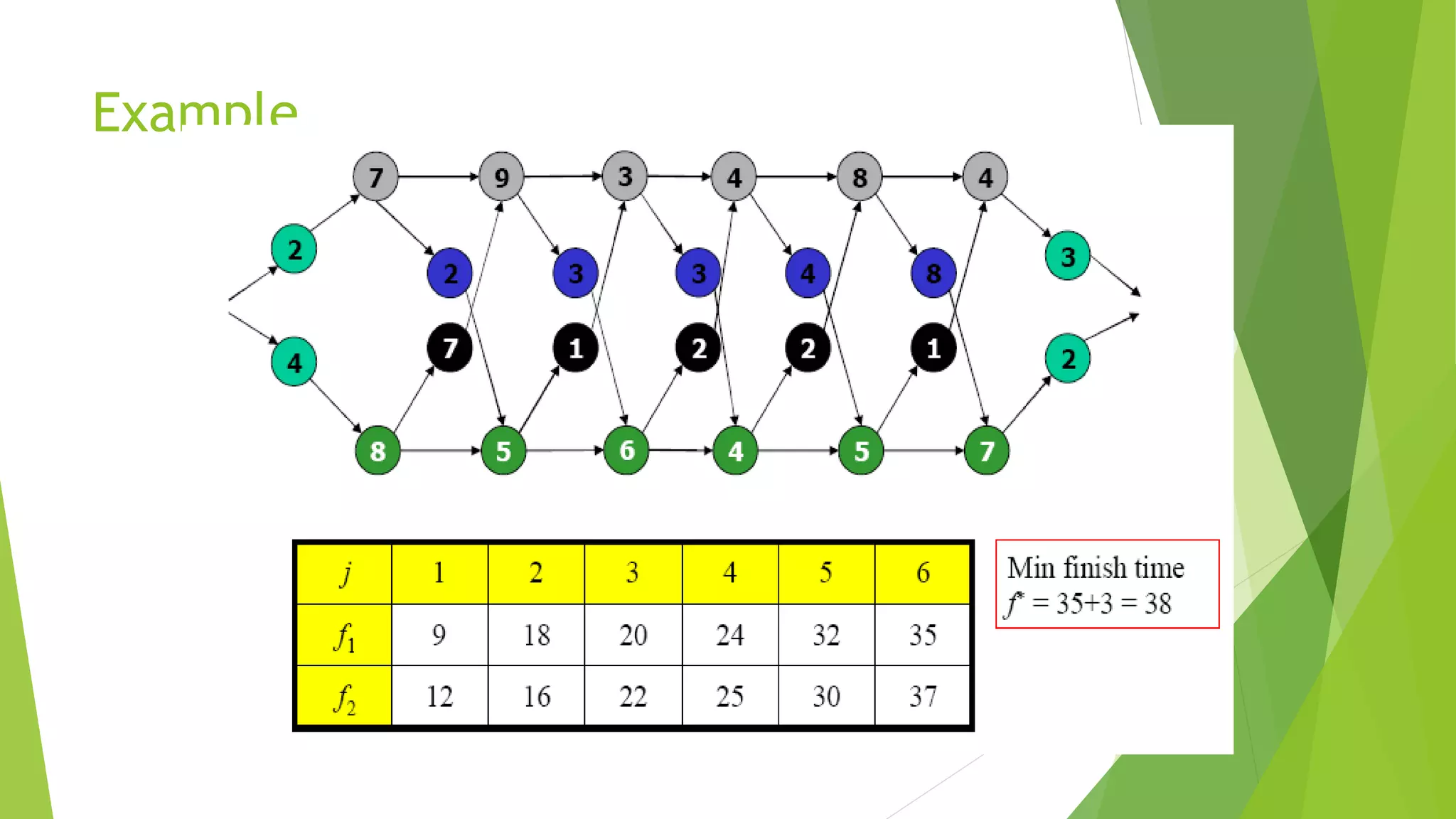
70. Step 2: Recursive Solution
 Using the values of l* and li[j] shown in Figure (b) in next slide, we would trace a
fastest way through the factory shown in part (a) as follows
 The fastest total time comes from choosing stations
 Line 1: 1, 3, & 6 Line 2: 2, 4, & 5

72. Step 3: Optimal Solution Value

73. Step 3: Optimal Solution Value

74. Step 3: Optimal Solution Value

75. Step 3: Optimal Solution Value

76. Step 3: Optimal Solution Value

77. Step 3: Optimal Solution Value

78. Step 3: Optimal Solution Value

79. Step 3: Optimal Solution Value

80. Step 4: Optimal Solution
 Constructing the fastest way through the factory

82. 1)`the process of breaking down a complex problem into
a series of interrelated sub problems often provides
insight into the nature of problem
2) Because dynamic programming is an approach to
optimization rather than a technique it has flexibility
that allows application to other types of mathematical
programming problems
3) The computational procedure in dynamic programming
allows for a built in form of sensitivity analysis based
on state variables and on variables represented by
stages
4)Dynamic programming achieves computational savings
over complete enumeration.

83. 1.)more expertise is required in solving dynamic programming problem then
using other methods
2.)lack of general algorithm like the simplex method. It restricts computer
codes necessary for inexpensive and widespread use
3.)the biggest problem is dimensionality. This problems occurs when a
particular application is characterized by multiple states. It creates lot of
problem for computers capabilities & is time consuming
Di