Flattening filter Free

Principal knowledge for commissioning of Linac
using FFF
Francisco J. Hern´andez Flores
franciscohernandez f2010@hotmail.com
MMP Student 2015 - 2016
May 26, 2016
Francisco J. Hern´andez Flores (Arcispedale Santa Anna, Ferrara Italy)Radiation Therapy May 26, 2016 1 / 22

1 Purpose
2 Introduction
3 Aspect of commissioning
4 Proﬁle normalization
5 Dosimetric ﬁeld size
6 Penumbra
7 Slope
8 The peak Position
9 Conclusion
10 References

Purpose
To investigate dosimetric characteristics of a new linear accelerator designed
to deliver flattened, as well as flattening filter-free (FFF), beams. To evaluate the
accuracy of beam modeling under physical conditions.[4]

Purpose
To know the possible deﬁnitions and suggestions for some dosimetric
parameters for use in quality assurance of FFF beams generated by medical
linacs in radiation therapy.

Purpose
To compare the dosimetric accuracy of advanced dose calculation algorithms
for ﬂattened (FF) and unﬂattened (FFF) photon beams.[5]

Purpose
To compare the dosimetric accuracy of advanced dose calculation algorithms
for flattened (FF) and unflattened (FFF) photon beams.[5]
We must to know the Dose calculation accuracy using Flattening filter free (FFF)
in Advanced treatment techniques, such as IMRT, VMAT and SBRT.

Introduction
In recent years, the clinical use of flattening filter free (FFF) beams is growing fast.
Among the reasons, the very high dose rate achieved (up to four times the dose rate
of the standard flattened (FF) beams plays a decisive role.
This allowed for stereotactic radiotherapy deliveries of very high dose per fraction (as
20 to 25 Gy) in very short treatment times, comparable with the conventional fraction-
ation time slots.
FFF beams have been extensively investigated and characterized before their intro-
duction in the clinical practice.[1]

Introduction
Flattening Filter
Conventional medical linear accelerators delivering photon beams are equipped
with a flattening filter (FF) in order to allow delivery of homogeneous dose
distributions with broad beams.
The differences between FFF and FF in terms of quality assurance is mainly
related to beam dosimetry, and not to mechanical characteristics of the linear
accelerator, for which the standard quality assurance procedures still hold.
Flattening Filter contribute to scattered, reduce dose rate, leakage from the
treatment head, beam hardening and also neutron fluence for high energy of X
ray used in Linac.[2]

Flattening Filter free beneﬁts
Increase the dose rate and reduce treatment time small treatment time less
patient movement.
Reduce leakage from the treatment head, they have 50% to 60% reduced
collimator and treatment head scatter.
reduced ”out of ﬁeld” dose obserbed to be less than 10% at 2 cm for a 6MeV
beams FFF, up to 20% reduced neutron contamination for 18MeV Beams [2]

Flattening Filter free beneﬁts
Increase the dose rate and reduce treatment time small treatment time less
patient movement.
Reduce leakage from the treatment head, they have 50% to 60% reduced
collimator and treatment head scatter.
reduced ”out of ﬁeld” dose obserbed to be less than 10% at 2 cm for a 6MeV
beams FFF, up to 20% reduced neutron contamination for 18MeV Beams [2]
Flattening Filter free Problem
Ion chamber and EPID saturation.
Inter leaf leakage, very high dose per pulse,
FFF can deposit dose of 1 Gy in 2.5 second inadvertent dose to critical
structures can be dangerous in extremely short time so therapist and patient
must be educated (24 Gy/min)

Quality Assurance of FFF beams
Flattening Filter Free (FFF)
FFF beams are used in the linac without FF in place of carousel. FFF delivered with
conventional medical linear accelerator have the conical flattening filter removed and
replaced by a thin foil.[2]
This foil is introduced for two reason:
For safety. It will stop the electron beam reaching the patient if the target
collapses.
Producing enough signal in the ion chamber by producing electrons.[1]
The main advantages of removing the flattening filter are an increased dose
rate, reduced scatter, reduced leakage and reduced out-of-field doses.[1]

Spectrum of two energy using FF and FFF
(a) spectrum of 6 MeV (b) spectrum of 10 MeV
Figure: Photon spectra for 6 MV FFF and 6 MV (left), and 10 MV FFF and 10 MV
(Right).

Profile normalization
The inflection point
Ponisch et al [3] suggested the use of the inflection point at the field edge to
renormalize a FFF beam to the same dose level of a FF beam. From this
renormalized profile it is then possible to evaluate penumbra and the field size.
The correct evaluation of the inflection point position is critical, being located
by definition at the point of the highest dose gradient. [1]
The re-normalization value
The use of a renormalization factor, compared to the inflection point procedure,
allows for a location of the normalization point in a less critical position, at the
profile shoulder, where the FF and the corresponding FFF profiles start to differ,
and it is located at the second maximum point of the third derivative of the
profile.
Renorm Factor =
a + b ∗ FS + c ∗ depth
1 + d ∗ FS + e ∗ depth
(1)

Profile normalization
Based on the fact that FFF beams deliver higher dose to the central axis, FFF and FF
beams should be mutually renormalized to superimpose the profile fall-off. Two meth-
ods can be followed: the inflection point or the renormalization value. Both methods
hold only for symmetric beams.
(a) Renormalization Point (b) Infection Point
Figure: Renormalization point obtained through the profile third derivative [1]

Dosimetric field size
Once the FFF beams are renormalized as above, the concept of dosimetric field size
as the distance between the 50% dose levels can be used for FFF beams, as for FF
beams [generally the full width half maximum (FWHM) is used for standard FF beams
normalized to 100% at central beam axis].
Alternatively, as suggested by Pnisch et al.[3] the distance between the left and right
inflection points could be used

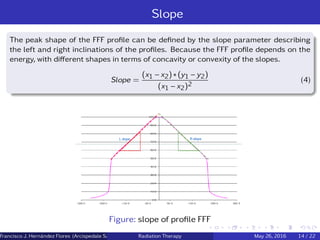
Penumbra
For conventional flattened-beam profiles, the definition of the penumbra is based on
the 80-20% dose values. This is not applicable in the unflattened case. Therefore, the
penumbra of the unflattened profile were derived from the spatial distance between
the positions where the doses were 20 and 80 % of the normalized dose Dn
Dn =
Du
Df
∗ DCAX (2)
Figure: Normalization of an unflattened profile of a measured 6-MV photon
beam. [3]

Flattened region and field region
The flatness is based on the flattened region definition, and should be applied to a
”field region” in a way that it could be used for both beam modalities. Once renormal-
ized as above, the ”field region” can be defined as the region within a certain defined
percentage of the field. The percentage could be the same for all field sizes, or it can
be changed.
Flatness and Unflatness
Unflatness is the parameter relative to FFF beams corresponding to flatness for FF
beams. Unflatness can be defined as the ratio between the dose level at the beam
central axis and the dose level at a predefined distance from the central axis as a
function of field size, or at the edge of the field region.
Unflatness =
Dosecentral axis
Doseoff axis
(3)

Slope
The peak shape of the FFF profile can be defined by the slope parameter describing
the left and right inclinations of the profiles. Because the FFF profile depends on the
energy, with different shapes in terms of concavity or convexity of the slopes.
Slope =
(x1 − x2) ∗ (y1 − y2)
(x1 − x2)2
(4)
Figure: slope of profile FFF

The peak Position
The peak of the FFF profile is the indication of the forward direction of the beam.
Intuitively this peak should be located on the beam central axis. The peak
position parameter is defined as the off-axis position of the intersection point of
the left and right slopes, as follows:
peakposition =
IL − IR
SR − Sl
(5)
where IL and IR are the left and right intercepts and SL and SR are the left and
right slopes,
I = y2 − x2 ∗
(x1 − x2) ∗ (y1 − y2)
(x1 − x2)2
(6)

Symmetry
Symmetry, as a parameter checking the equality level between left and right sides of a
profile, can be defined as usual for standard FF beams, with the only difference that the
evaluation area should be within the field region for FFF beams instead of the flattened
region commonly used in FF beams.[1]
The maximum dose ratio :
Dx
D−x max
(7)
The maximum Variation : (Dx − D−x)max (8)
where Dx and D−x are the doses at x and -x positions (symmetric relative to central
axis).
The area ratio :
LeftIntegral − RightIntegral
LeftIntegral + RightIntegral
(9)
where LeftIntegral and RightIntegral are the areas bounded by the profile on the left
and right of the beam central axis.

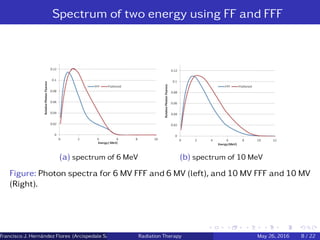
Energy spectrum and quality index
FFF beams present an energy spectrum significantly different from FF beams
since the thick conical shaped attenuator is removed.[1]
Despite the differences in the FFF spectrum with respect to the corresponding FF
beam, there is no reason to change quality index definitions that can be.[1]
QI = 1.2661 ∗
D20cm
D10cm
− 0.0595. (10)

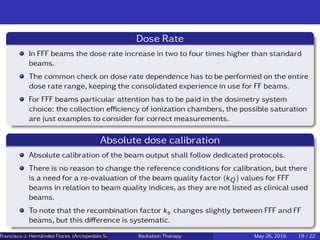
Surface Dose
Due to different electron contamination and lower photon energy spectrum, surface
doses of FFF are expected to be different from FF beams.18 The surface dose param-
eter Ds is defined here as the relative dose at d = 0.5 mm with respect to the dose
at dmax.Due to different electron contamination and lower photon energy spectrum,
surface doses of FFF are expected to be different from FF beams. The surface dose
parameter Ds is defined here as the relative dose at d = 0.5 mm with respect to the
dose at dmax.[1]
Output Factor
The head scatter component of a FFF beam relative to the corresponding FF
beam is markedly different. Variation in output factors is then less pronounced
for FFF beams due to the head scatter component.[1]
Output factor definitions are kept identical for both FFF and FF beams.[1]
In both setup conditions the output factors of FFF fields are less spread, in
particular for in air evaluation, confirming the lower head scatter component for
such fields.[1]

Dose Rate
In FFF beams the dose rate increase in two to four times higher than standard
beams.
The common check on dose rate dependence has to be performed on the entire
dose rate range, keeping the consolidated experience in use for FF beams.
For FFF beams particular attention has to be paid in the dosimetry system
choice: the collection eﬃciency of ionization chambers, the possible saturation
are just examples to consider for correct measurements.

Dose Rate
In FFF beams the dose rate increase in two to four times higher than standard
beams.
The common check on dose rate dependence has to be performed on the entire
dose rate range, keeping the consolidated experience in use for FF beams.
For FFF beams particular attention has to be paid in the dosimetry system
choice: the collection eﬃciency of ionization chambers, the possible saturation
are just examples to consider for correct measurements.
Absolute dose calibration
Absolute calibration of the beam output shall follow dedicated protocols.
There is no reason to change the reference conditions for calibration, but there
is a need for a re-evaluation of the beam quality factor (kQ ) values for FFF
beams in relation to beam quality indices, as they are not listed as clinical used
beams.
To note that the recombination factor ks changes slightly between FFF and FF
beams, but this diﬀerence is systematic.

Conclusion
Removing the flattening filter improved the characteristics of the accelerator in terms
of smaller penumbras especially for the 18-MV mode, reduced MLC leakage, and less
variation in the total scatter factors.[3]
Although the FFF beams provide much high dose rate at the treatment target, the ion
recombination effect of the Farmer, PinPoint, and plane-parallel chamber in the FFF
photons is not significantly different from the flattened photons. These ion chambers
are suitable in the quality assurance and exposure measurement for the FFF beams
regarding their negligible ion recombination and sufficient collection efficiency.
We have presented ideas regarding the quality controls (QC) that have to be consid-
ered during the establishment of a quality assurance program (QA) when introducing
FFF beams into a clinical setting.

References
A.Fogliata et al, Definition of parameters for quality assurance of flattening
filter free (FFF) photon beams in radiation therapy, Oncology Institute of
Southern Switzerland, 3 October 2012
Dhuruvan Viswanathan, flattening Filter Free LINAC, RPD 331 Hales , 17 August
2014
Falk Pnisch, Properties of unflattened photon beams shaped by a multileaf
collimator, Houston Texas 77030, 08 April 2006
JAN HRBACEK, Commissioning of the photon beams of flattening filter-free linear
accelerator and the accuracy of beam modeling using an anisotropic analytical
algorithm, Department of Radiation Oncology, University Hospital Zurich, Zurich,
Switzerland, Elsevier, 2011.
Gabriele Kragl et al, Radiation therapy with unflattened photon beams:
Dosimetric accuracy of advanced dose calculation algorithms,Article from
Department of Radiotherapy Medical University of Vienna, 23 July 2011

Many thanks for your kind attention

Flattening filter Free

More Related Content

What's hot

Viewers also liked

Similar to Flattening filter Free

More from Centro Nacional de Radioterapia Nora Astorga

Recently uploaded

Flattening filter Free