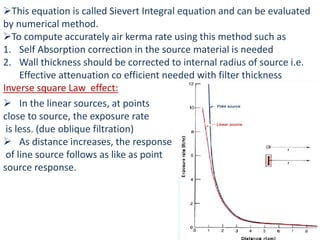
This document discusses brachytherapy dosimetry using the TG-43 formulation. It begins by introducing brachytherapy and the sources commonly used, such as iridium-192 and iodine-125. It then covers how sources are specified and calibrated, including using exposure rate constants, air kerma rate constants, and apparent activity. Methods for source calibration include air ionization chambers, well chambers, and solid phantoms. Dose distribution around sources is also discussed, including using the Sievert integral for line sources. The TG-43 formalism provides a standardized method for calculating dose around brachytherapy sources.

1. Brachytherapy Dosimetry
(TG 43 Formulation)
SABARI KUMAR P
M.Sc. Radiation Physics

2. OUTLINE
Introduction
Sources used in Brachy
Source Specification and its relation
Source Calibration Methods
Exposure Rate Method
Well type chamber Method
Solid Phantom Method
 Dose Distribution around sources
TG 43 Formulation

3. Introduction
Brachytherapy also named as Curie Therapy or Radium Therapy
It is a special type of Radiotherapy treatment technique in which
irradiation happen by placing radio nuclide inside or near the tumor
A high dose can be delivered locally to the tumor with rapid dose
falloff in the surrounding tissues
It generates highly conformal dose distribution in the target volume
Mainly two types of sources are used such as:
Sealed sources: Two sources with same activity may emit different
amount of energy due to encapsulation. Hence dose rate may differ.
 Unsealed sources: Due to no encapsulation, two sources with same
activity emit same amount of energy. Hence dose rate becomes same.

4. Based on source placement,
different classifications done in
Brachytherapy such as
 Intracavitary Brachytherapy :
- source is placed in body cavities
 Interstitial Brachytherapy
- source is inserted into tumor
 Surface Mould
- source is placed externally near the tumor
 Intra Luminal & Intra Vascular
- sub classification of Intracavitary

5. Based on dose rate used to treat tumor again Brachytherapy classified
as
Low dose rate (LDR) : <2Gy/h dose rate
Medium Dose rate (MDR): >2Gy/h to <10Gy/h dose rate
High Dose rate(HDR) : >10Gy/h dose rate
Pulse Dose rate (PDR) : <1Gy/h HDR becomes used as PDR
Based on source used in Brachytherapy, again two techniques
introduced such as
Permanent Implantation : Au-198, I-125, Pd-103
Temporary Implantation : Cs-137, Ir-192, Co-60 and Ra-226

6. Desirable Properties of Brachytherapy Sources:
 Source may be naturally available or artificially obtained
 Optimum Gamma ray emission should be high enough to avoid
increased energy deposition in bone and to minimize scatter. At the
same time, it must be low to meet protection requirements
 Long Half life is required for permanent storage and decay correction
should minimum
 Charged Particle emission should be absent
 Should not be gaseous disintegration product
 should have high specific activity
 Possible to available in different shapes, sizes
 should be insoluble, nontoxic and not in powder form

7. Sources used in Brachytherapy
1. Radium -226: First source used in Brachytherapy. It is a naturally
available source. It decays to Pb-206 by emitting 0.83MeV (Average)
energy. Due to high exposure, hazardous bi-product (Radon – 222)
and low specific activity ( 0.98 Ci/g) present usage stopped
permanently.
2. Cesium 137: Cs- 137 is a nuclear fission by product and decays to
Ba -137 by emitting 0.662MeV gamma energy. Its low specific
activity (50Ci/g) limited this usage in LDR only.
3. Cobalt – 60: Co-60 is a neutron activated product, which decays to
Ni-60 by emitting 1.25MeV (Average) energy. High specific activity
(200 Ci/g) makes its wide usage in Brachy earlier. But due to short
half life (5.26Y) and cost effective, no longer used at present in
Brachy.
4. Gold – 198: Au-198 is produced by nuclear activation and it decays
to Hg-138 by emitting 0.412MeV energy. Short half life ( 2.6days)
makes this usage in permanent implantation technique.

8. 5. Iodine – 125: It decays via Electron Capture to Te-125 and emits
0.35MeV gamma energy. Relatively longer half life (59.4 days),
gained more advantage in permanent implant technique over
Au-198, Rn-222. But dosimetry is much more complex due to
complex energy spectrum.
6. Palladium – 103: It is the substitute for I-125. It decays to Rh-103 via
electron capture and emits 0.021MeV energy. Having short half life
(17 days) compared to I-125, it may provide biologic advantage in
permanent implants.
7. Iridium -192: It is more popular as a replacement of Ra-226. It
decays to Pt-192 by emitting 0.361MeV (Average) energy. High
Specific activity ( 400 Ci/g) and short half life (73.8 days) makes this
source more popular in temporary implantation in HDR.
8. with all above, few of other Radioactive isotopes such as
Ytterbium – 169, Thulium – 170, Phosphor – 32, Yttrium - 90 and
Californium – 252 also used in Brachytherapy.

9. Source Specification
Each Brachy source has a specified source strength that is used to
calculate dose rate.
Source strength can be stated in terms of one of several interrelated
physical quantities such as – Radium Equivalent Mass, Apparent Activity,
Air Kerma Rate (RAKR), Air kerma Strength, Exposure Rate .
Radium Equivalent Mass:
Ra-226 was predominant source in Brachy in early days. So source
strength was defined by Mass of Ra
For non Radium sources, strength can be specified by Ra Eq. Mass
Relation between mg Ra Eq and its activity is
1 mg Ra Eq = 1 mCi of Ra

10. Exposure Rate Constant:
The exposure rate constant defines as the Exposure at a unit distance
from the point source of activity A
gamma
Here Ʈδ = Exposure Rate constant (R–m2/Ci – hr (or) R-cm2/mCi - hr)
r = Distance from source and Measurement point (P) (m2)
X(P) = Exposure at point P (R)
A = Activity of source (Ci)
Conditions :
1. Source should be a bare point source
2. The photon fluence is neither attenuated nor scattered in the
distance ‘r’
3. When δ = 0, the exposure rate constant includes all the photons
emitted by the radionuclide
A
)P(X.r2


11. Air Kerma Rate Constant:
From the relation between exposure (X), air kerma (Ka) and Exposure
rate constant,
Here Ka is expressed in μGy/hr
Units: μGy – m2/Ci – hr
Reference Air Kerma Rate (RAKR):
If Air kerma rate is defined at 1 meter distance and corrected for air
attenuation and scattering, then it becomes Reference Air Kerma Rate
(RAKR).
It is indicated by KR(dref)
Units: Gy/Sec
a
2
k, K
A
r


12. Apparent Activity:
Basically, the source is not bare point source. It is encapsulated by
filter material which introduces an attenuation. Thus reduction in air
kerma rate happens. To compensate this attenuation effect, Apparent
Activity is introduced.
If the source is calibrated under Air kerma rate conditions, the source
strength may be specified as Apparent Activity or Effective Activity.
Here Aeff = A x Katt
Katt – source encapsulation attenuation
Thus, Apparent activity can be determined by dividing measured air
kerma with Air kerma rate constant (or) exposure rate with exposure
rate constant.
Ka
a
2
eff
)P(K.r
A



13. Air Kerma Strength:
This was introduced by AAPM in 1987 to replace exposure rate.
The product of air kerma rate in free space and the square of the
distance of calibration point from the source centre is called as Air
kerma Strength.
Sak = Ka x r2 (or) Ʈak x Kattn x A
Units: μGy m2/hr
 For linear sources, Ka is measured at a point along the mid
perpendicular line of the source at a distance very much larger than
active length of the source.
1 μGy – m2/hr = 0.138 mg Ra Eq
 AAPM 43 recommends a shorthand
notation for air kerma strength as “U”
1 U = 1 μGy – m2/hr

14. Standardization of Brachytherapy Sources
As like external beam therapy measurements, Brachytherapy
measurements should also be traceable to the Primary standardization
lab.
In Brachy, sources are standardized in terms of RAKR or Air kerma
Strength.
Based on the source strength, three methods are developed.
1. Measurement using air setup with ion chamber
2. Measurement using well type ion chamber
3. Measurement using Solid Phantom of well defied geometry
In Air measurement setup

15. Measurement using Air setup:
The arrangement consists of a large source to ion chamber distance
relative to source and detector dimensions.
 For this a calibrated large volume chamber can be used for low
activity sources.
Calibration method for large volume chamber in Lab :
Ka at 1 meter (at point P) for working standard : X Gy/h
current at P for the large volume chamber : Y pA
Air kerma calibration factor NK = (X/Y) Gy/pA . hr
For a source to be calibrated , consider the current reading Y’ at point
P, then
Ka of the source at P = NK . Y’ Gy/h
After applying Air attenuation factor (Kattn) and Scatter Radiation
correction factor (Kscatt) and non uniformity correction factor (Kn)
the KR becomes
KR = NK. Kattn . Kscatt . Kn . Y’

16. Corrected Reading Y’ = M . Ku. Kt. KP. KTP. Kion. Kv. Kwall. Kappl
M – Meter Reading (pA)
Ku – Unit conversion factor from air to water/medium
Kt – Transit time correction factor
KP – Polarity correction factor
KTP – Temperature and Pressure correction factor
Kion – Ion recombination factor
Kv – chamber volume correction factor
Kwall – chamber wall attenuation & scattering correction factor
Kappl – Applicator attenuation correction factor
Generally NK – air kerma calibration factor for Co-60 and Cs-137 can
provided by PSDL or SSDL. For other than these sources, Interpolation
between two neighboring calibration point is used.
 For low energy radio nuclides ( I-125 and Pd-103) large volume
chambers are required at the same time, for routine clinical procedures,
this method is not practical.

17. Well chamber Measurement:
Most widely used method for calibration sources of any radio nuclide
by using Well type ion chamber (or) 4πr-chamber (or) isotope calibrator
(or) Re-entrant type ion chamber.
Calibration of well chamber is made either
1. with source previously calibrated using air setup
2. with source of the same radio nuclide calibrated by a PSDL
These chambers are calibrated in terms
of RAKR or Air kerma Strength.
Source Strength of a Brachy source by using
well chamber is determined from,
KR = NKR . M . KP . KTP . Kion. Kappl
Here,
NKR – RAKR calibration factor of chamber

18. Cont..
Due to thicker walls of well type chamber, the energy and source type
dependence of the response of well type chambers are much more
pronounced.
Energy dependence of the chamber arises from absorption and
scattering of photons and secondary electrons in the chamber walls and
the gas.
The oblique filtration through the source encapsulation affects the
chamber response by photon absorption and thus produces change in
the energy spectrum.
Source dimensions and source position in well chamber also affects
the chamber response.

19. Measurement using Solid Phantom:
Phantom Measurement is superior than air measurement and
equivalent to well type chamber measurement.
 The RAKR or Air Kerma Strength depends on phantom specific
geometry, material and radio nuclide to be used.
 The generalized formula for all sources and
all solid phantom designs published by DGMP as
KR = NK . M . KαP . Kph
Here
NK – Chamber Calibration Factor
M – corrected Meter Reading
KαP - Perturbation correction factor
(Medium changing from air to Phantom)
Kph - Phantom correction factor density correction factor
from water to water equivalent meterial
 To minimize the source position dependence,
a plastic SF catheter is used.

20. Dose Distribution of Brachy sources
In early days the treatment were purely empirical based on trail and
error i.e certain amount of Ra (mg) is placed for certain (hours) to treat
various types of tumors. This was popular as “mgh” method. But at
present, new techniques came for dose distribution calculations around
the source.
The kerma rate at a point in air or in tissue from seed can be
calculated using Air kerma Rate Constant
The dose at a point from line source can be determined using Sievert
Integral Method.
For ideal Point source:
1. The air kerma rate can be calculated based on the RAKR and inverse
square law, at point of interest in air becomes
Ka(r) = Kr (r0/r)2
2. The absorbed dose rate to air in air becomes
Da(r) = Kcol,a(r)
= Ka(r) . (1.- g) = Kr . (1- g) . (r0/r)2

21. 3. The absorbed dose rate to water in air medium becomes
Dw(r) = Da(r) . (μen/ρ)a,w
= Kr . (1- g) . (r0/r)2 . (μen/ρ)a,w
4. The absorbed dose rate to water in water medium becomes
Dw(r) = Kr . (1- g). (r0/r)2 . (μen/ρ)a,w . fas,w(r)
In terms of Air kerma strength,
Dw(r) = Sk. (1- g). (1/r)2 . (μen/ρ)a,w . fas,w(r)
From the above equation, one can conclude that the absorbed dose is
depends on emitted photon energy spectrum (radio nuclide ) , distance,
absorption and scattering on medium , g value and mass energy
absorption coefficient.
But Practically g values are zero for Brachytherapy sources. The mass
energy absorption coefficient for high energy radio nuclides is
insensitive to source designs. Thus the photon spectra changes due to
source design only. So the above equation can re-written as
Dw(r) = Kr . (r0/r)2 . (μen/ρ)a,w . fas,w(r)

22. For Line source: (In air)
In real situation, the source is not a point source. Sources have finite
dimensions. At This condition, the total source length is dividing into
small elementary sources and applying Inverse Square Law and
filtration corrections to each
Consider a source of active Length ‘L’ and filtration ‘t’.
The kerma rate Ka at point ‘P’ contributed by
the source element dx length is given by,
Here
A – Activity
Ʈka – Air Kerma rate constant
μ’ – Effective attenuation co-efficient for filter
By integrating the above equation and taking account of θ1 and θ2


 



de
L
dx
Y
A
)P(K
2
1
/
tSec.ka
a

 tSec.
2
ka
a
/
e
L
dx
r
A
)P(dK

23. This equation is called Sievert Integral equation and can be evaluated
by numerical method.
To compute accurately air kerma rate using this method such as
1. Self Absorption correction in the source material is needed
2. Wall thickness should be corrected to internal radius of source i.e.
Effective attenuation co efficient needed with filter thickness
Inverse square Law effect:
 In the linear sources, at points
close to source, the exposure rate
is less. (due oblique filtration)
 As distance increases, the response
of line source follows as like as point
source response.

24. In Medium:
 For calculation of the dose in water or medium, the perturbation
correction (WPC) for this distance, WPC(Y Secθ) should be
incorporated in the integral expression.
Here
WPC – (Kattn)w.(Kscat)w
Limitations:
The Sievert Integral method will not account for filtration in the paraxial
regions (A & A’) (introduces significant errors and practically break
downs in the extreme oblique directions)
A A’
)YSec(WPC.de
L
dx
Y
A
)P(K
2
1
/
tSec.ka
a 

 




25. Modular Dose Calculation Model : TG 43
In 1995, AAPM – TG 43 taken calculation model proposed by ICWG
and published recommendations on dosimetry formalism and dosimetry
parameters for Interstitial Brachytherapy sources.
Primarily, these were considered only for LDR sources. But later,
virtually implemented to HDR and PDR also.
Previous dose calculations were based on apparent activity,
Eq. Mass of Ra, Exposure Rate constants and tissue attenuation
coefficients. These did not account for source to source differences in
active core constructions and encapsulation design.
The TG 43 introduced and incorporated dose rate constants and
specific source design dosimetric parameters.
TG 43 is simple to implement and small number of parameters are
used which can easily extract form Monte Carlo calculated dose rate
distribution around the sources in a water equivalent medium.

26. For the reference point of TG 43 formalism becomes,
Dw(r0,θ0) = Kr . G(r0,θ0) . (μen/ρ)a,w . fas,w(r0,θ0) -----------(1)
For the point of interest, TG 43 formalism becomes,
Dw(r,θ) = Kr . G(r,θ) . (μen/ρ)a,w . fas,w(r,θ) -----------(2)
From the above equations,
Dw(r,θ) = Dw(r0,θ0). G(r,θ)/ G(r0,θ0) . fas,w(r,θ)/ fas,w(r0,θ0)
= Sk . Dw(r0,θ0)/Sk . G(r,θ)/ G(r0,θ0) . fas,w(r,θ)/ fas,w(r0,θ0)
Finally , the equation can re written as,
Dw(r,θ) = Sk . Λ . G(r,θ)/ G(r0,θ0) . g(r) . F(r,θ)
Where,
Λ = Dw(r0,θ0)/Sk (dose rate constant)
g(r) . F(r,θ) = fas,w(r,θ)/ fas,w(r0,θ0)
P
R
θ
θ

27. Reference Medium :Water (Homogeneous medium)
Reference Data : Monte Carlo Simulation data
Source Geometry : All Clinically approved source dimensions
Reference Dose calculation
point : A point lying on the transverse
bisector of the source at a distance
of 1cm from its center that’s why r0
Point of Measurement : Dose rate at point which is on radial line
at an angle w.r.to source
Formalism: Dose = S x dose rate constant x inverse square law factor x
absorption/scatter correction factor in the medium x
absorption/scattering correction factor in the source
Here Sak – Air kerma strength in U
G(r,θ) – geometric function at radial distance r and polar angle θ
for point source ==> G(r,θ) = 1/r2
for line source ==>G(r,θ) = (θ -θ )/LY
),r(F)r(g
),r(G
),r(G
S),r(D
00
ak 




28. G(r0,θ0) – geometric function at reference point (r0 = 1 cm and θ0 =900)
g(r) – Radial dose function which depends on photon absorption and
scatter in the medium along the transverse axis
F(r,θ) – anisotropy function that considers the effects of absorption and
scatter of the photons within the source active core and
encapsulation material.
It is defined as The angular dependence of the dose rate value
for a given radial distance r, corrected for the distance related effect
using the effective inverse square law correction.
)90,cm1r(G)90,cm1r(D
)90,cm1r(G)90,r(D
)r(g 0
00
0
00
0
00
0



),r(G)90,cm1r(D
)90,cm1r(G),r(D
),r(F 0
00
0
00




29. Λ (Lamda) – Dose rate constant
It is defined as the dose rate to water in water at the reference
point (1cm, 00) per unit air kerma strength Sk.
This will depends on both the radionuclide and source design.
If source is a point source then,
Φan – distance dependent average anisotropy function
φan = 4π average dose rate /dose rate along the transverse axis
ak
0
00
S
)90,cm1r(D 

an2ak )r(g
r
1
S)r(D 

30. THANKYOU…
Need to better well