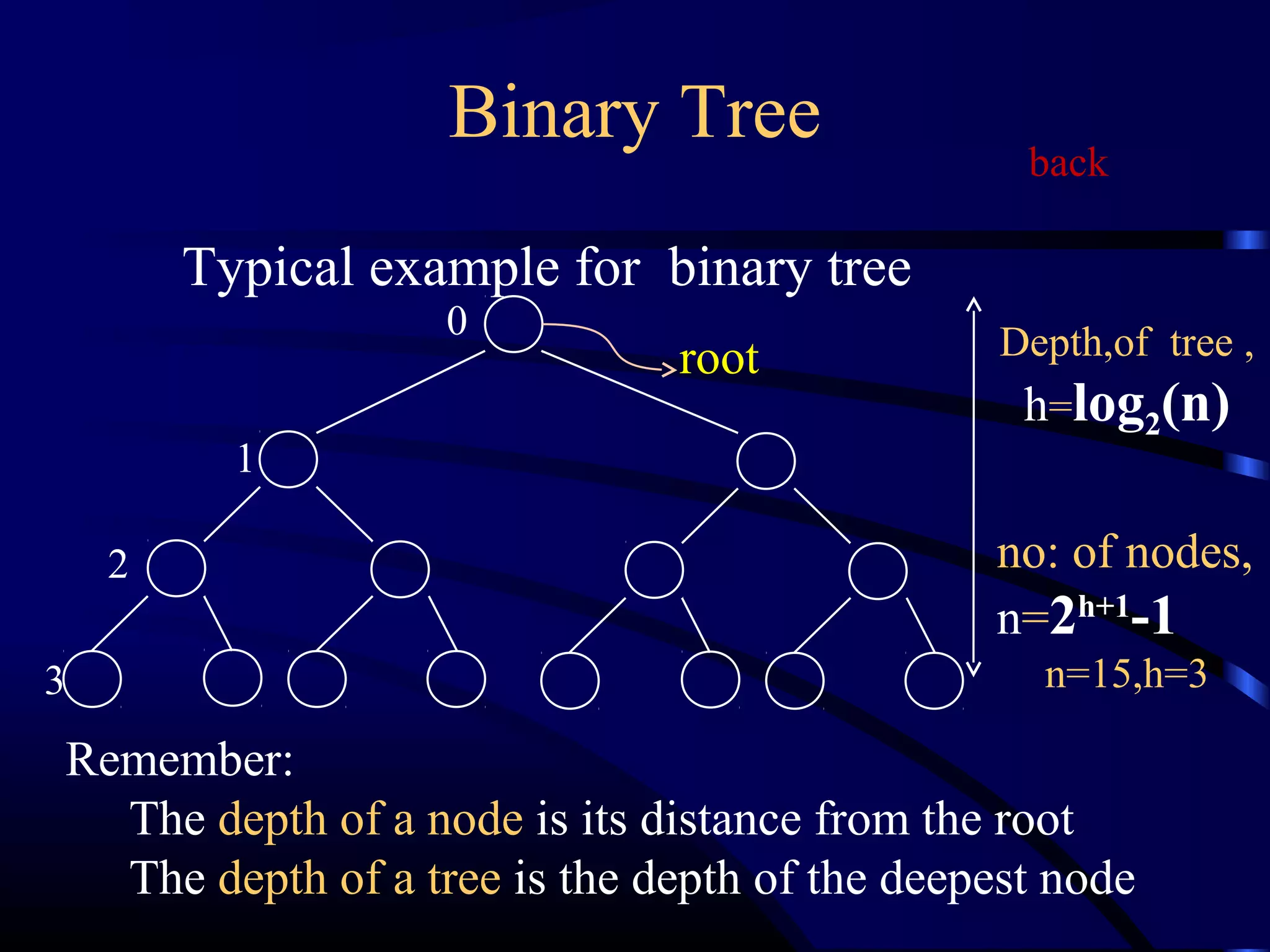
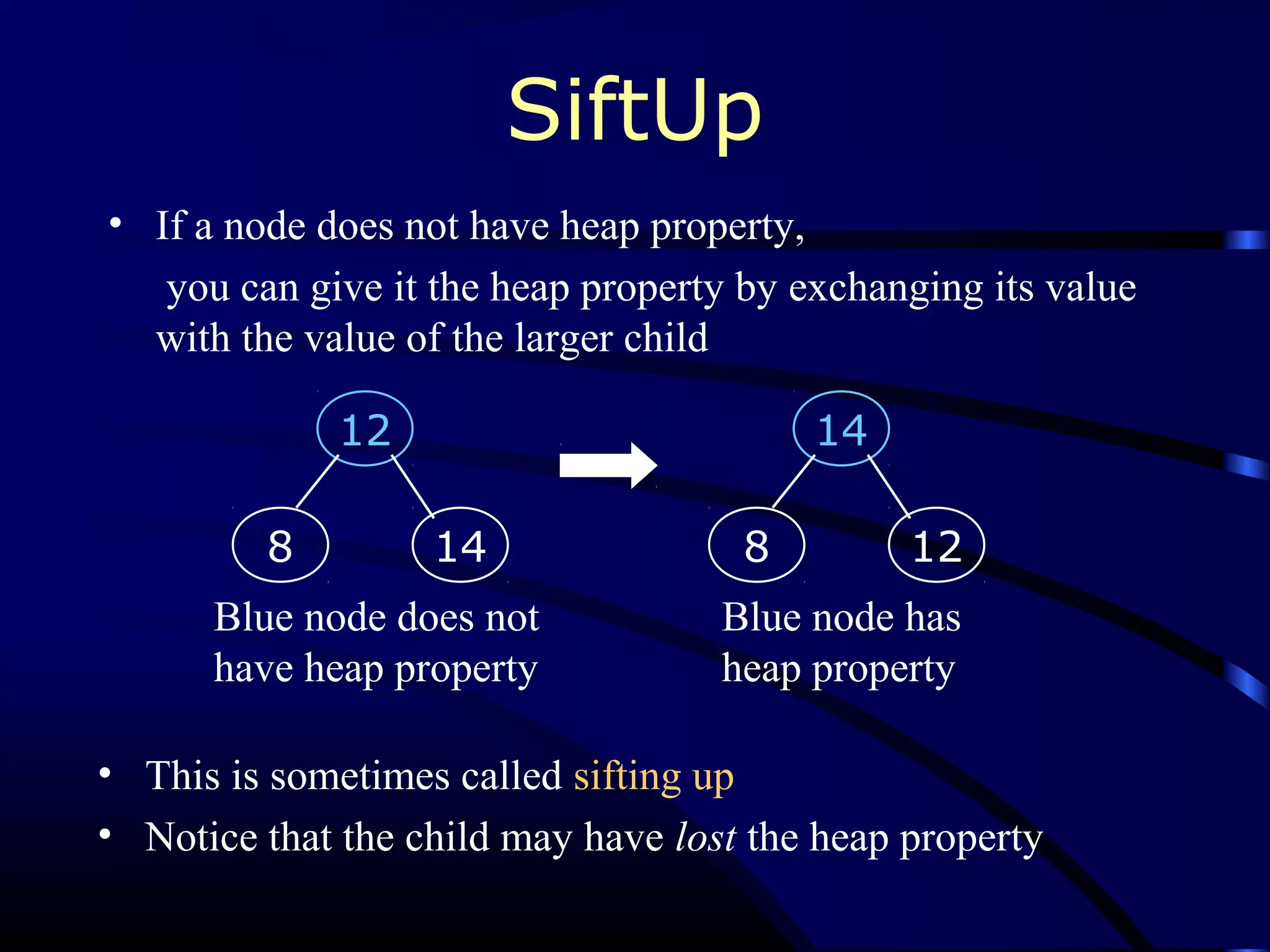
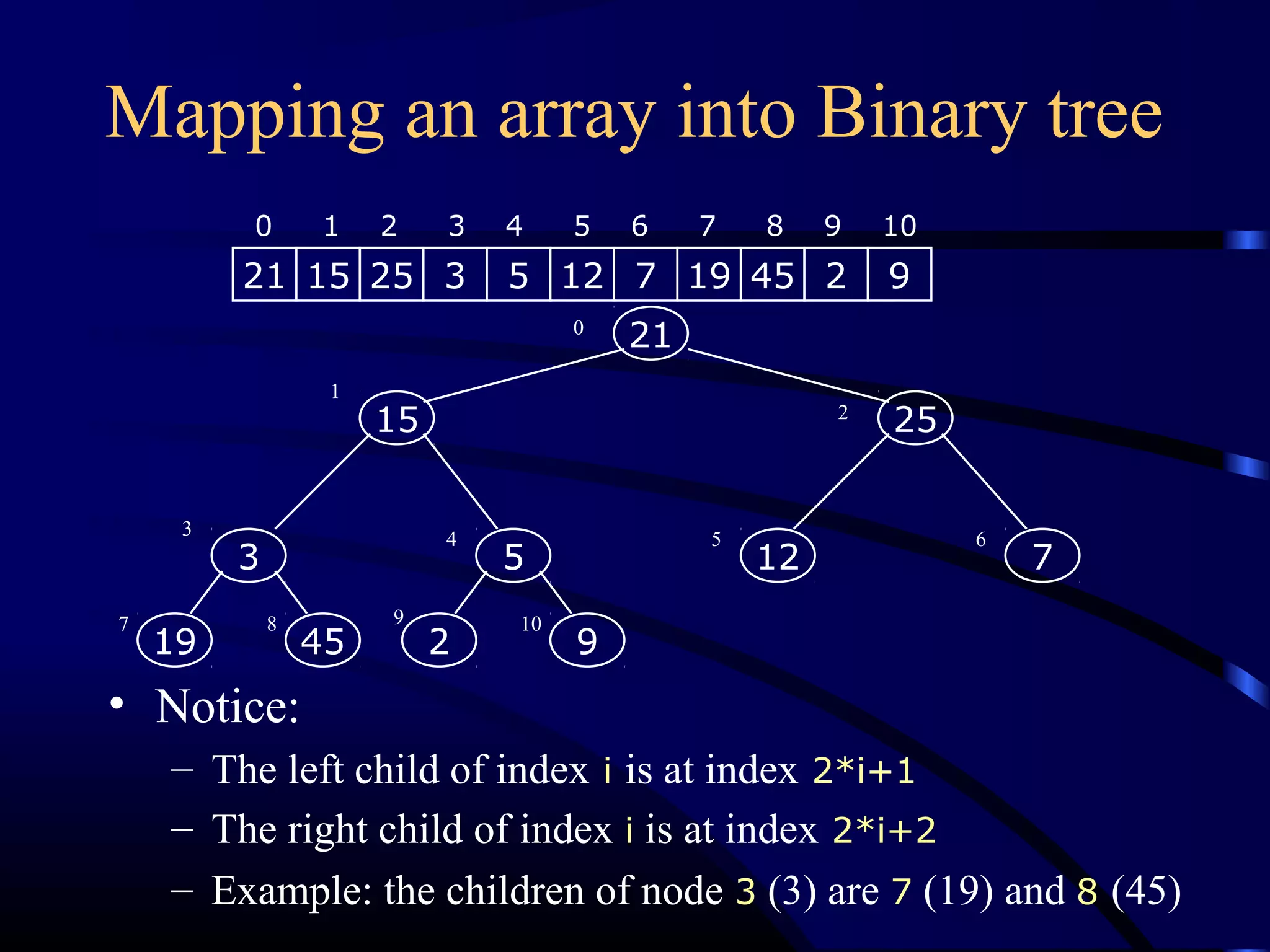
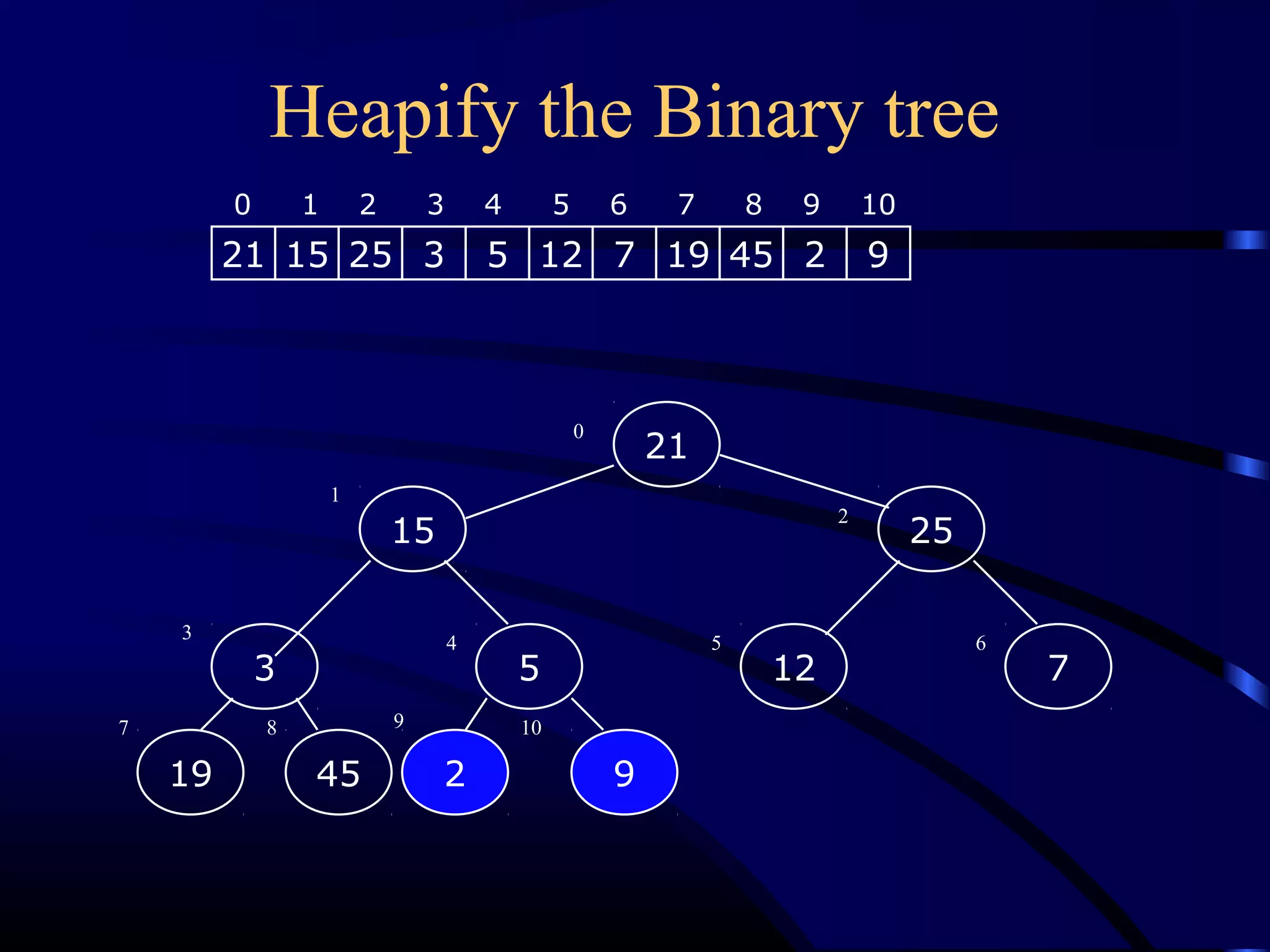
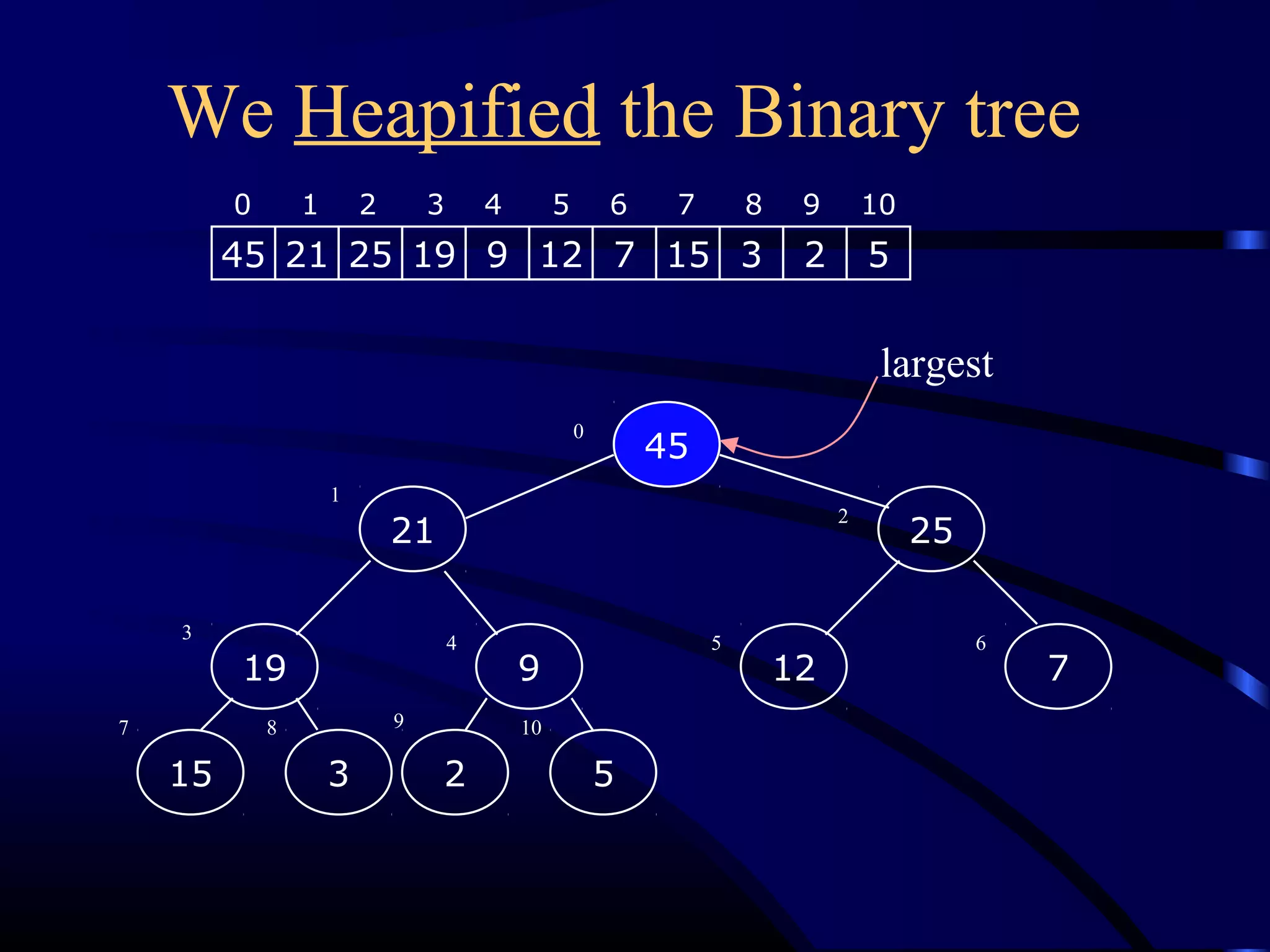
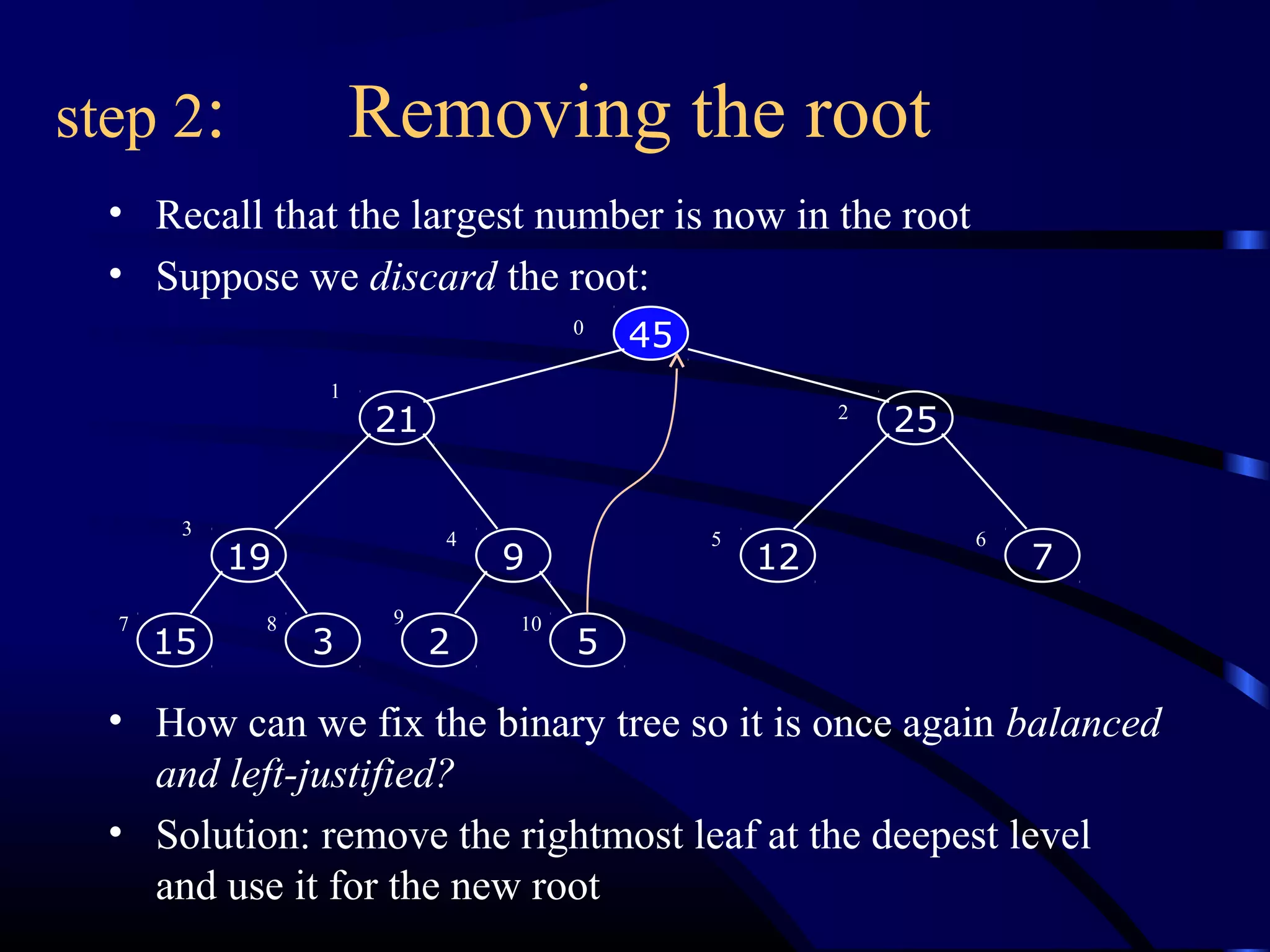
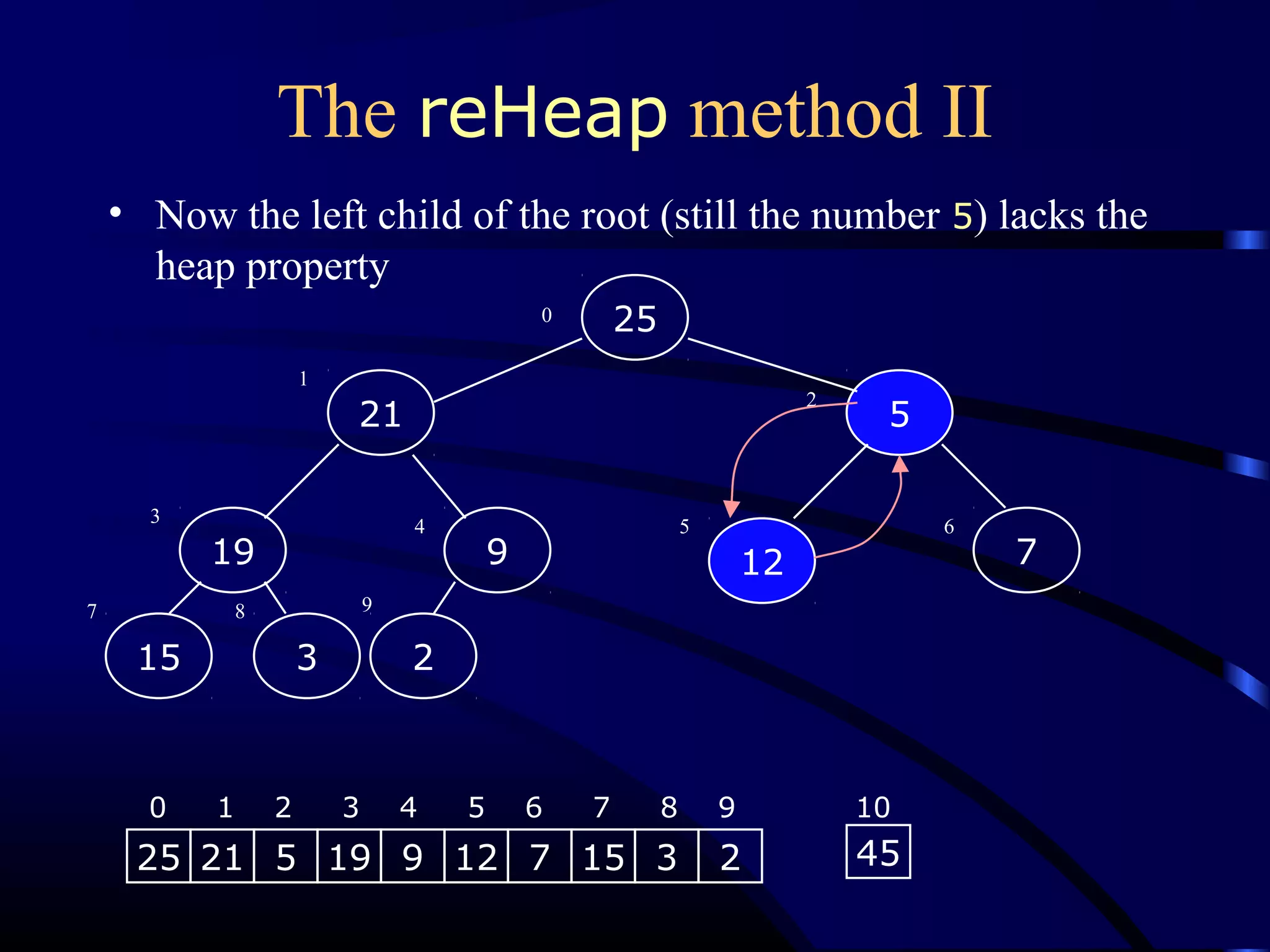
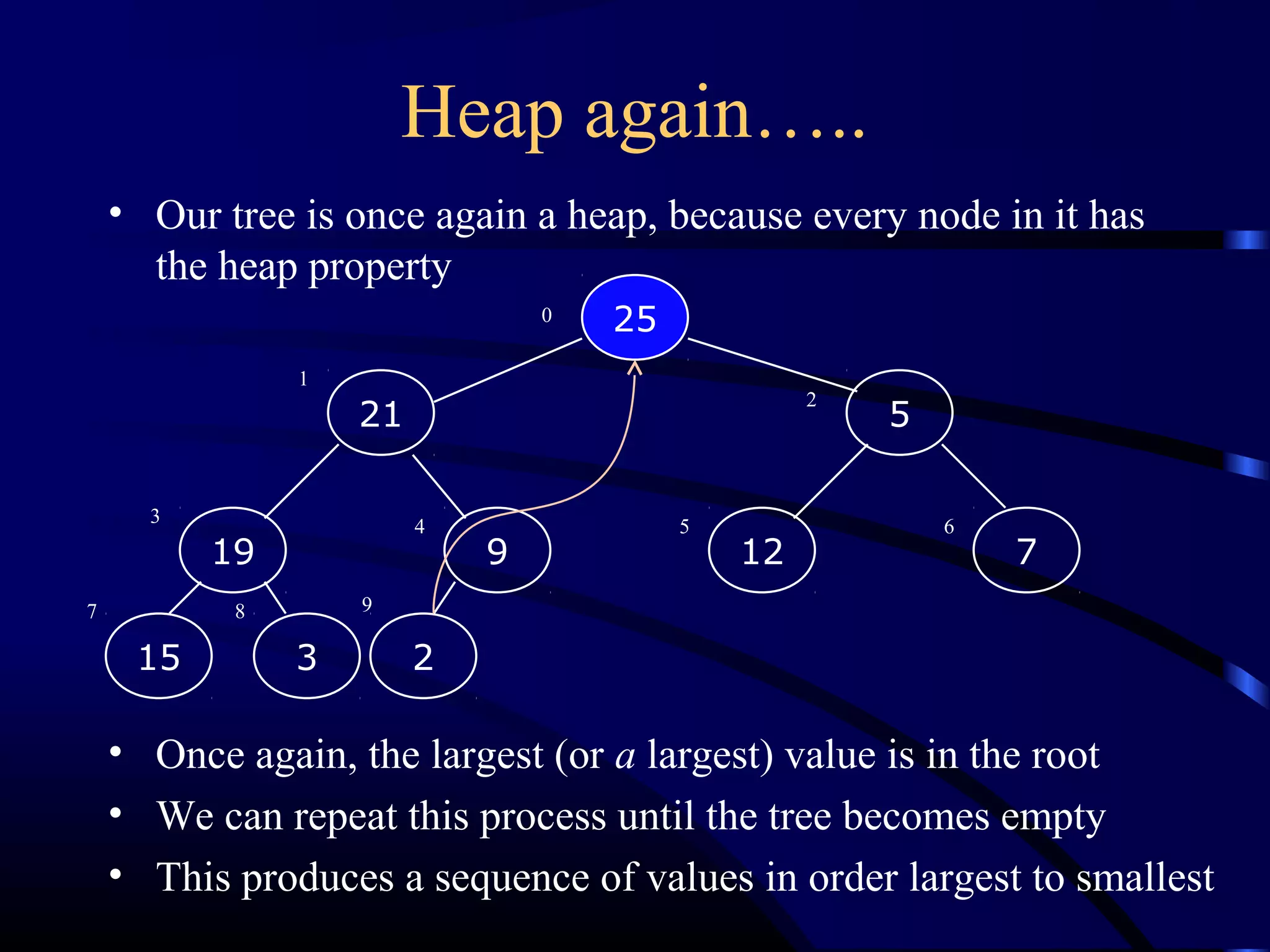
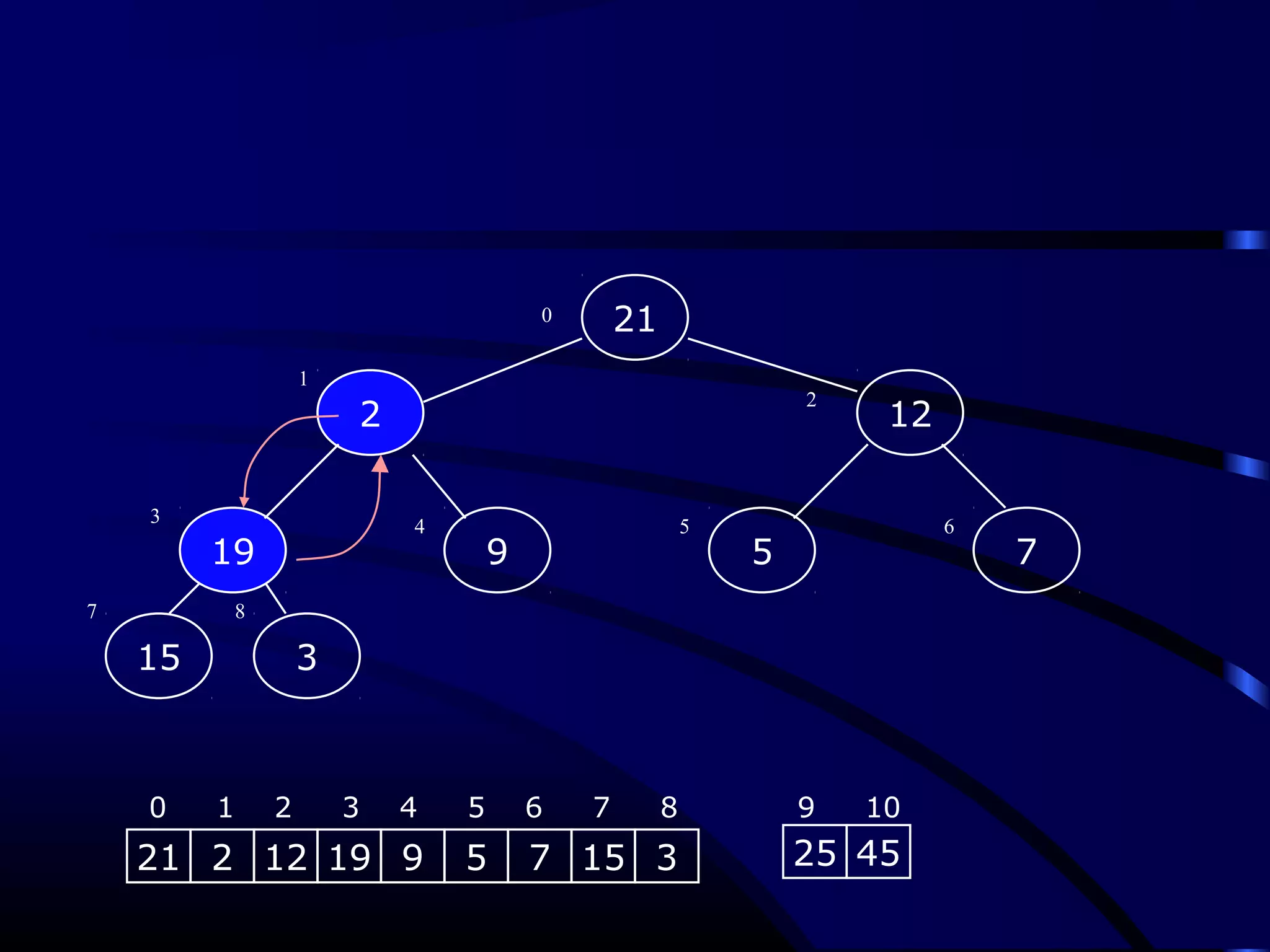
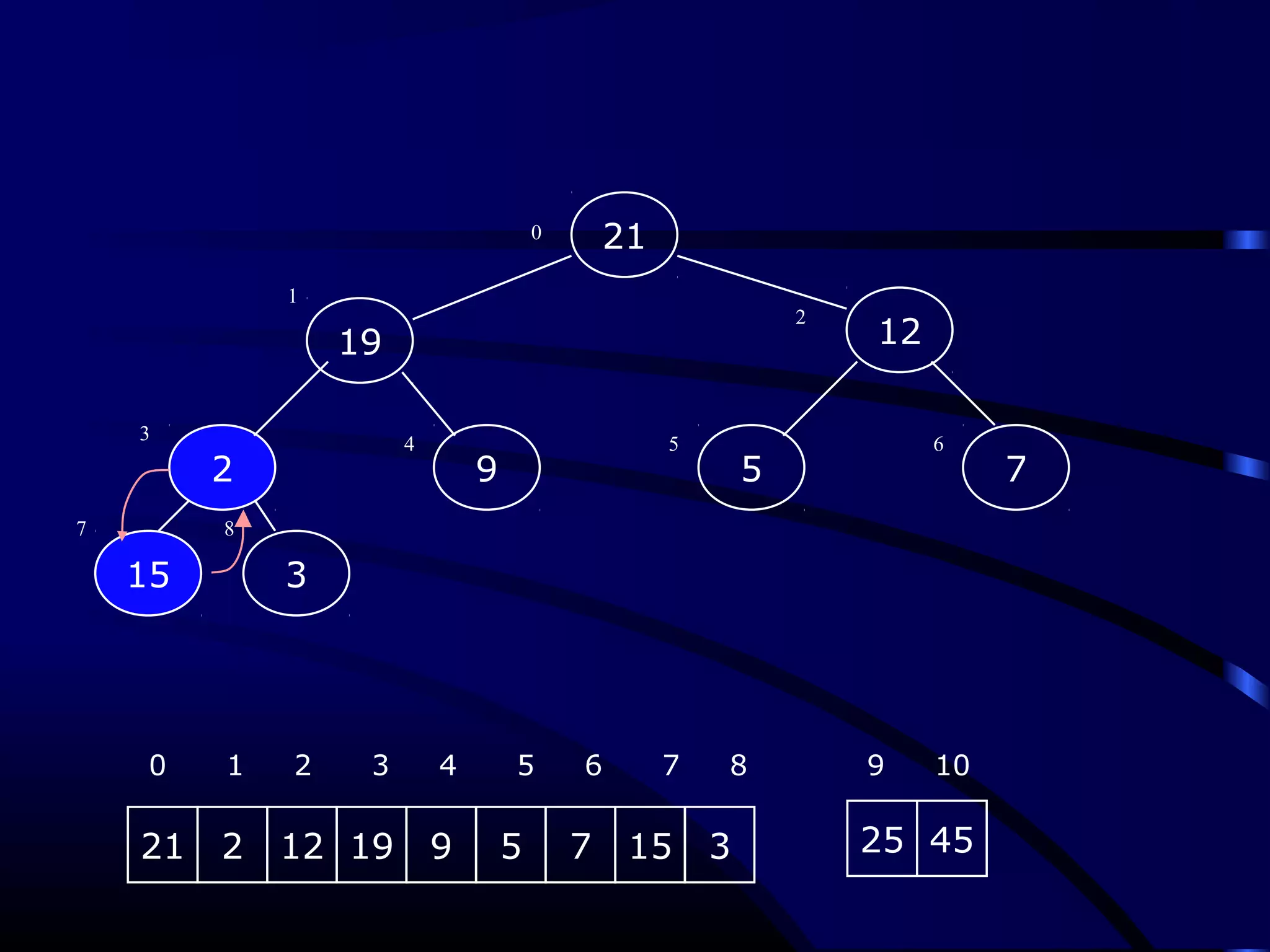
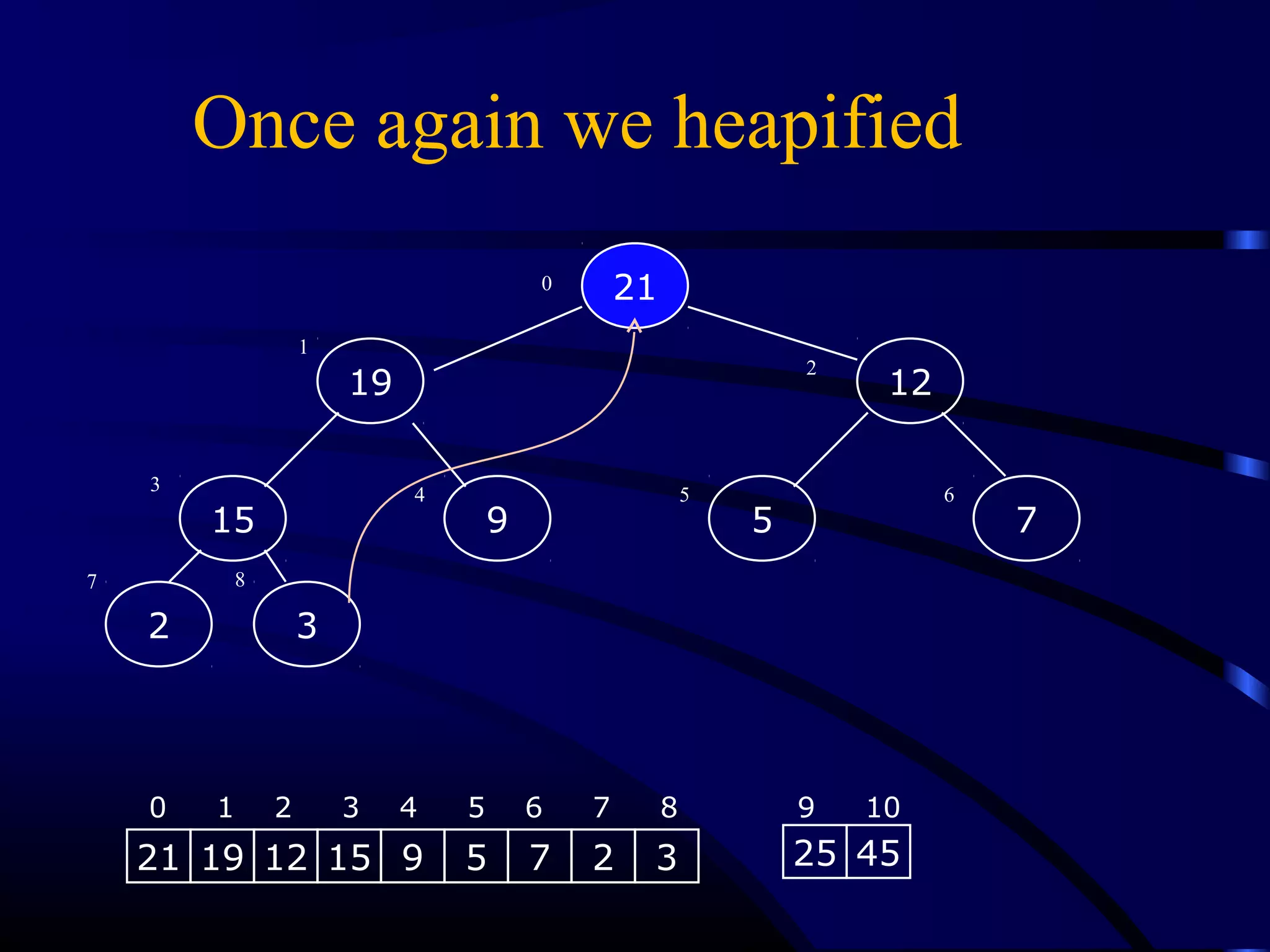
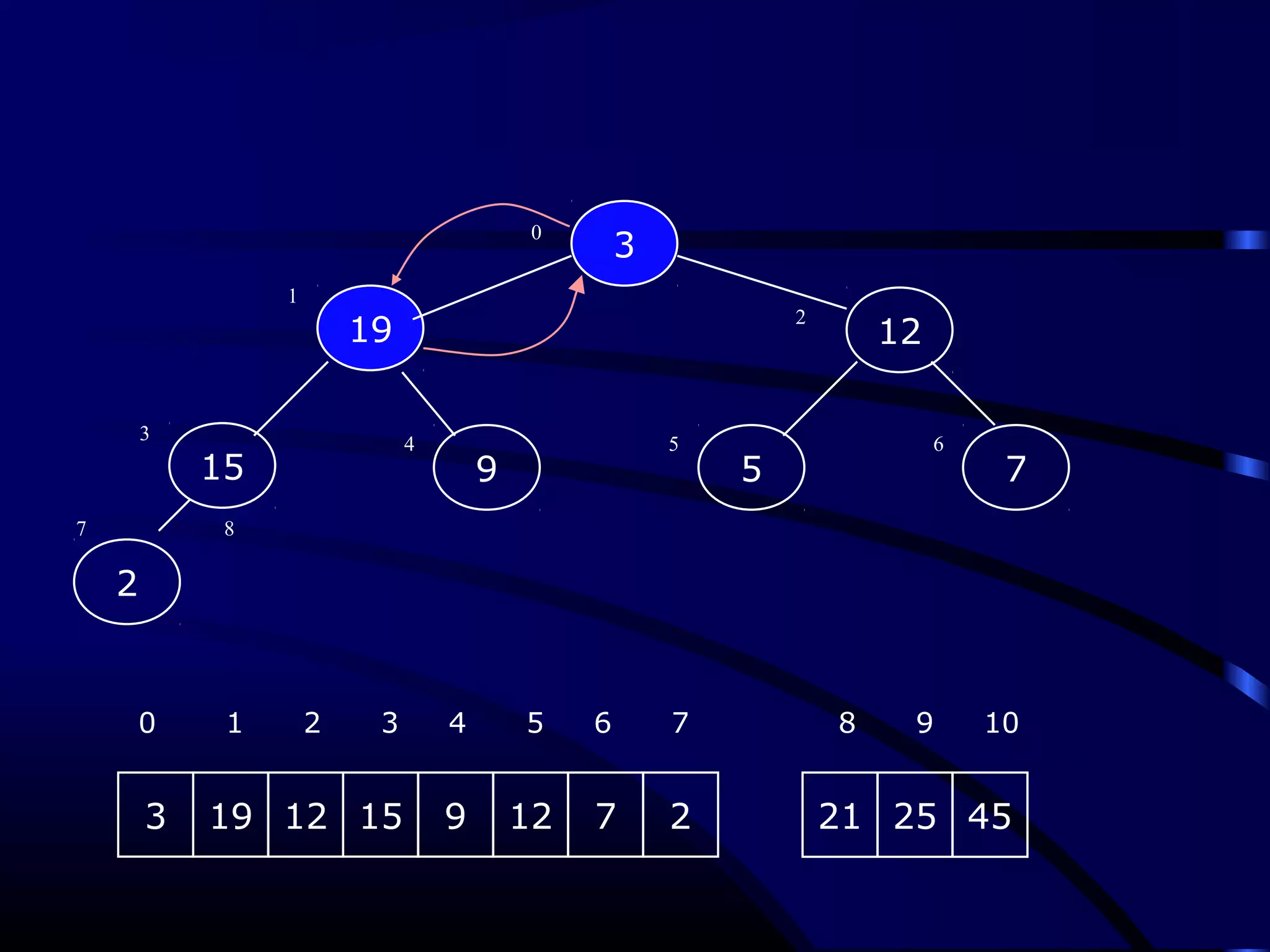
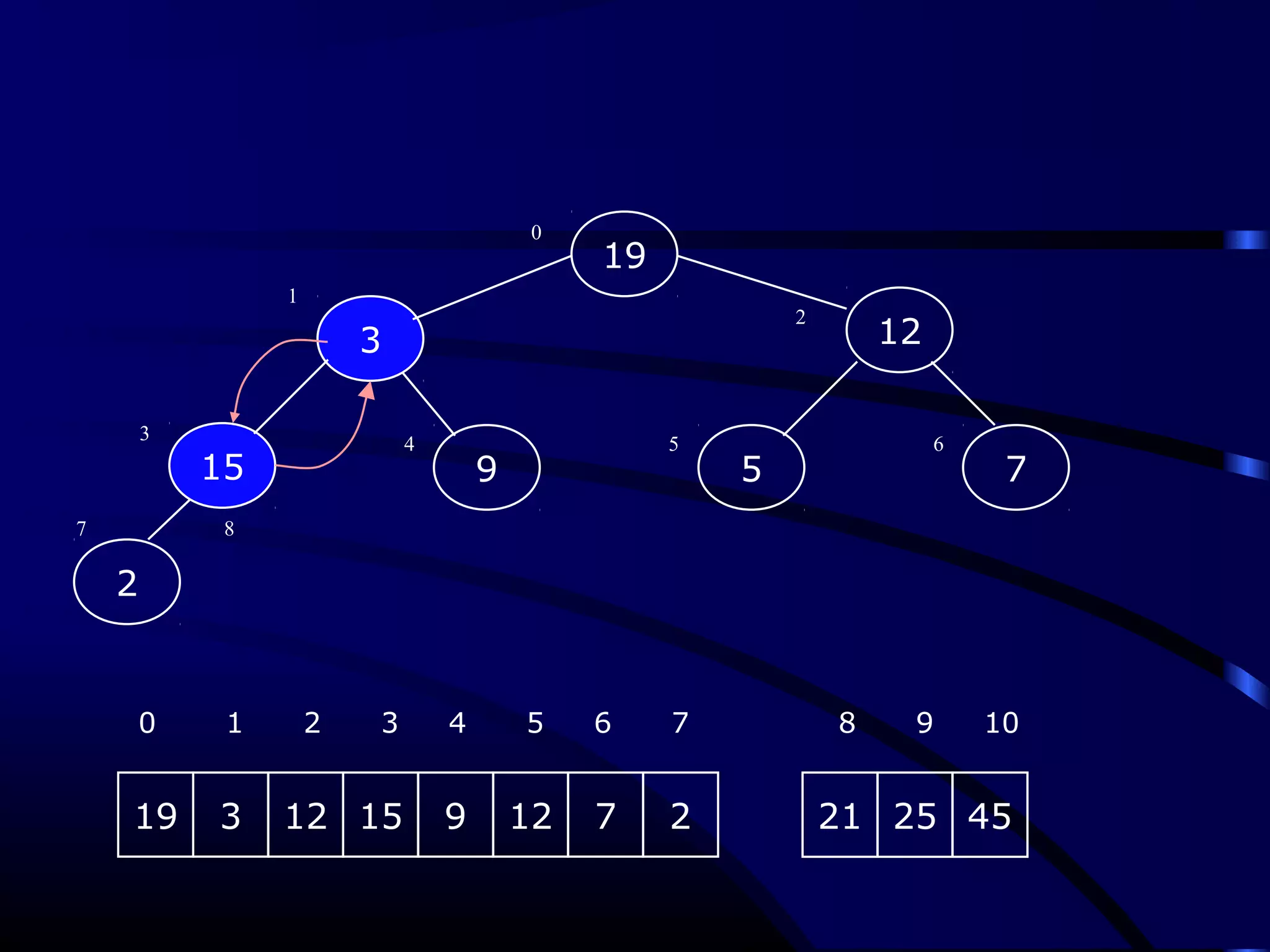
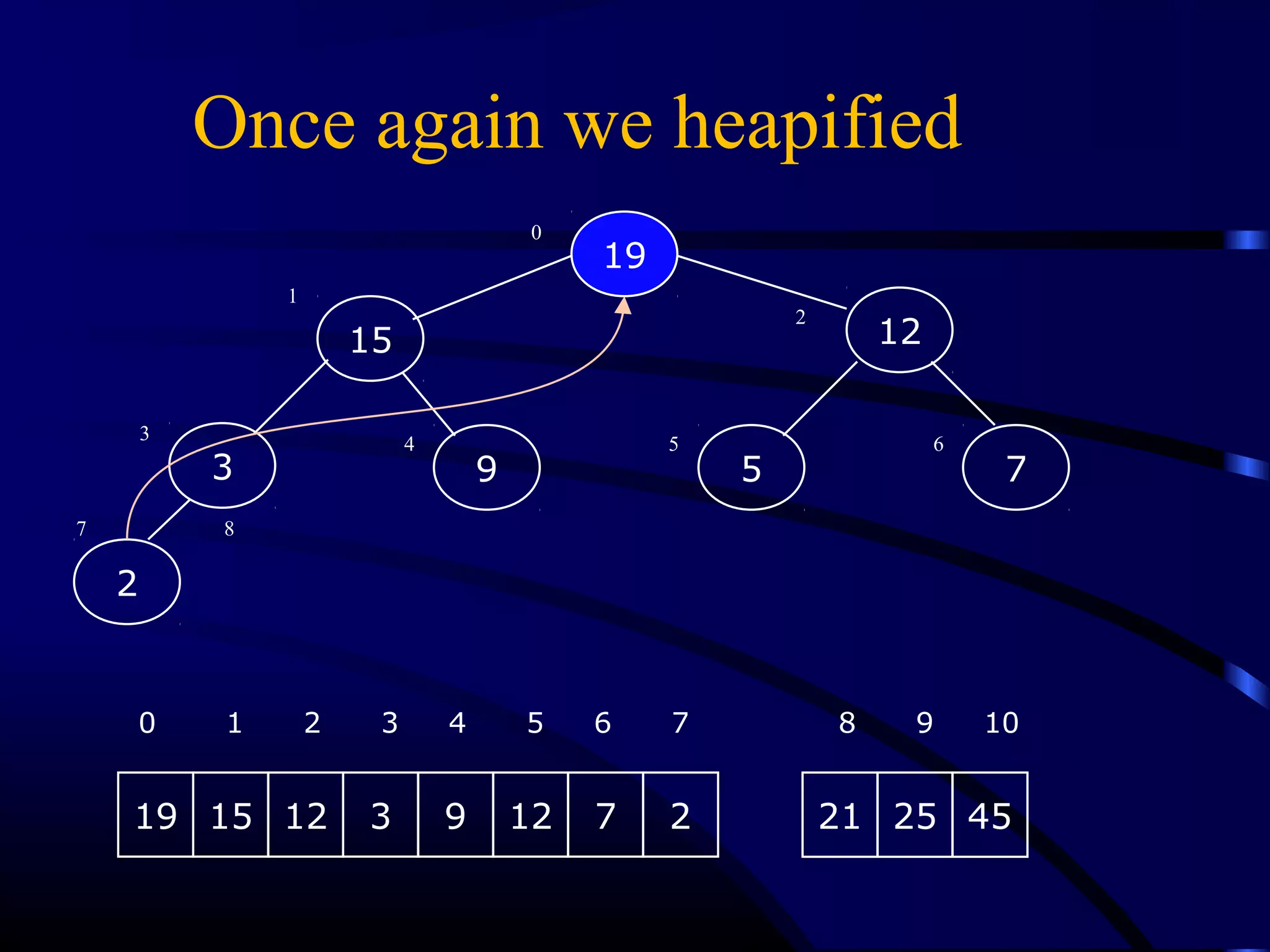
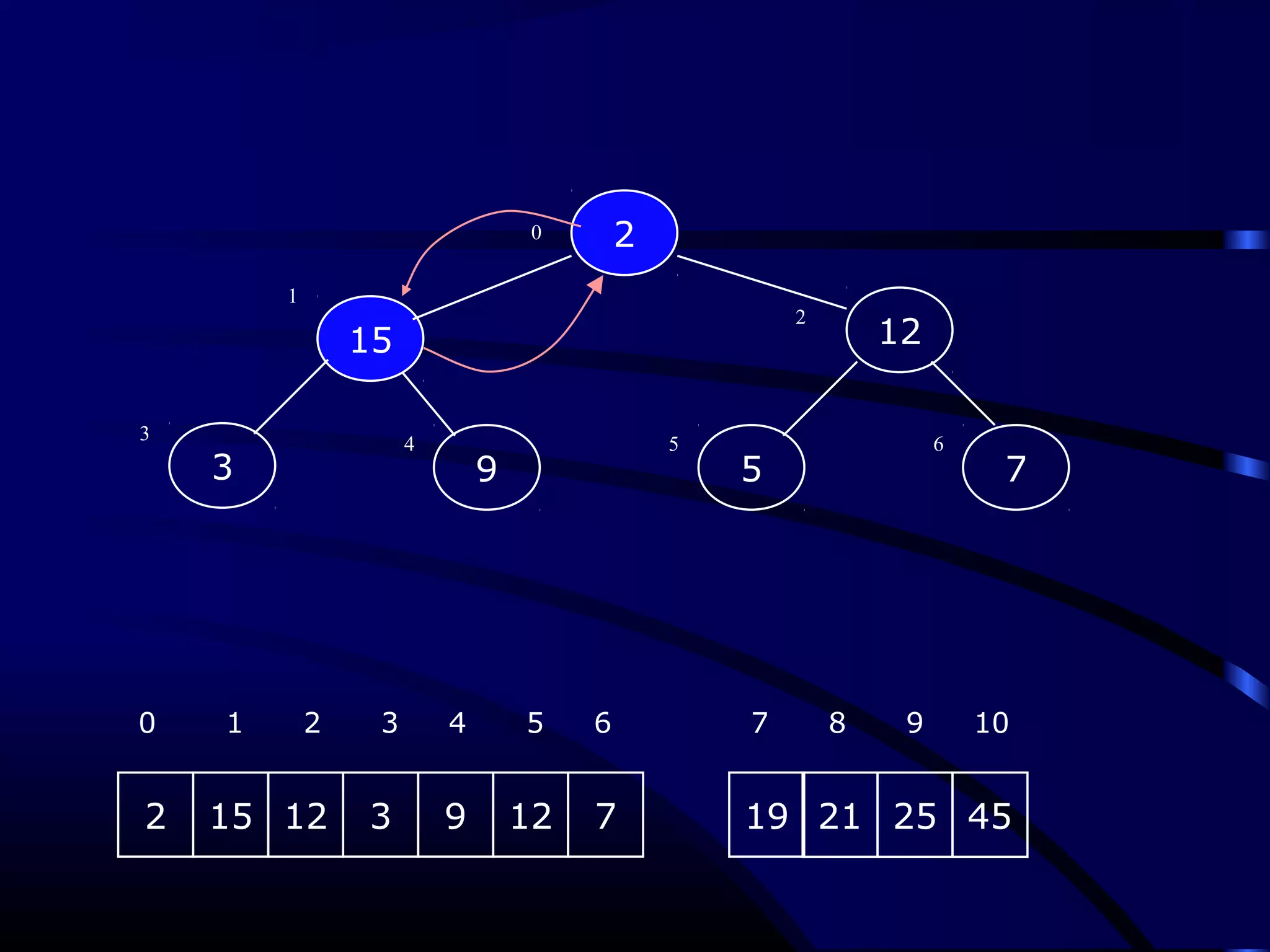
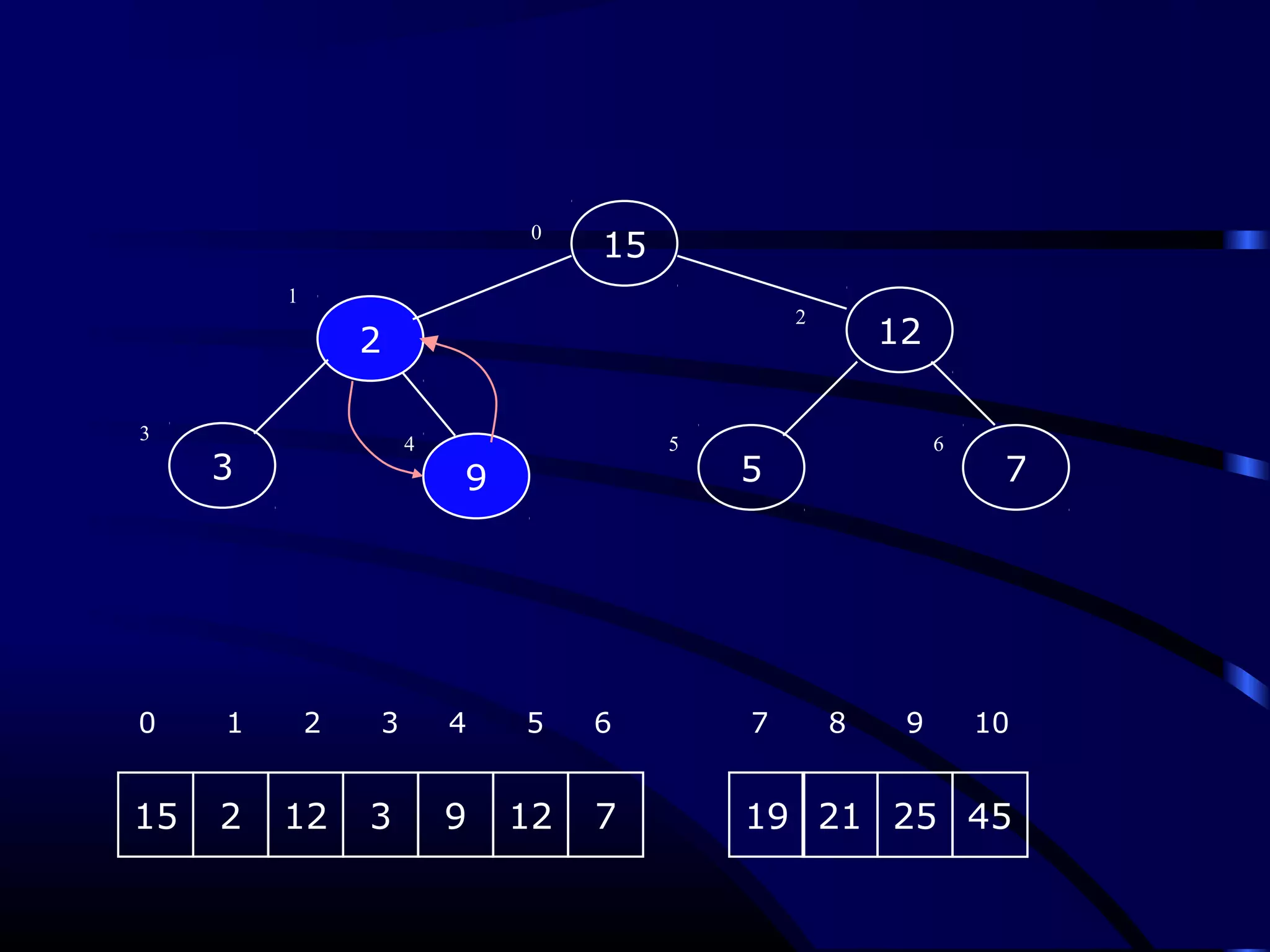
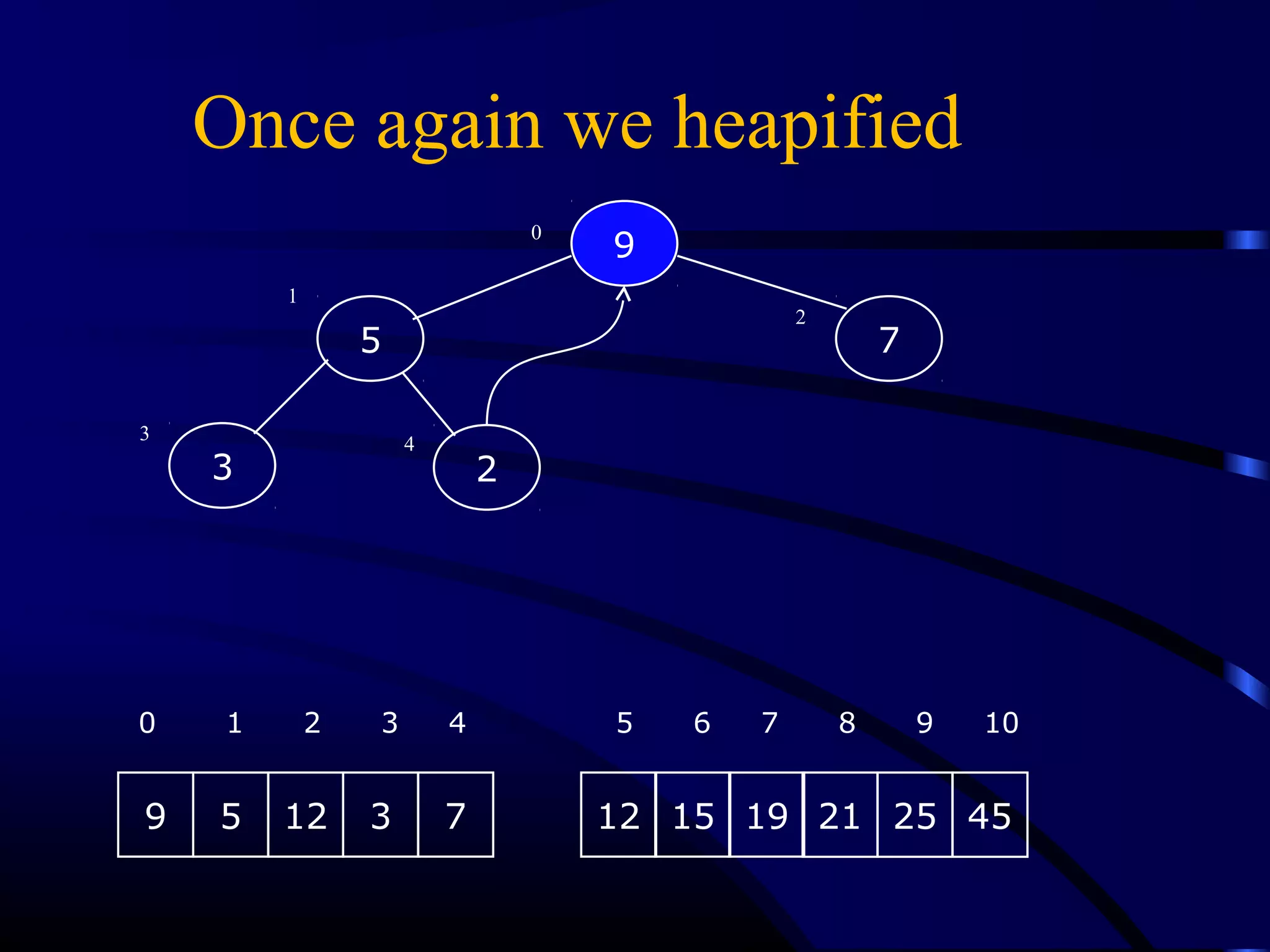
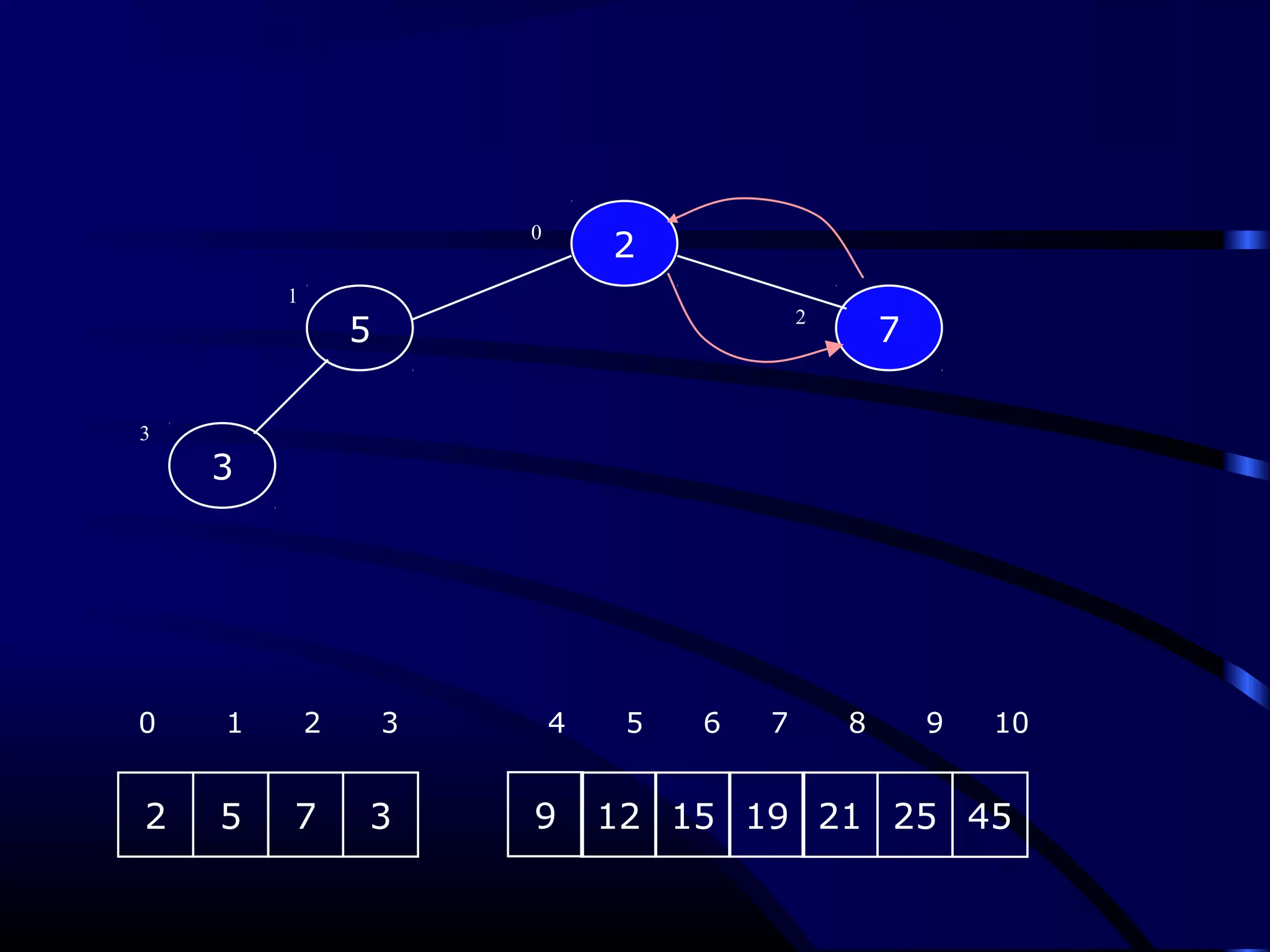
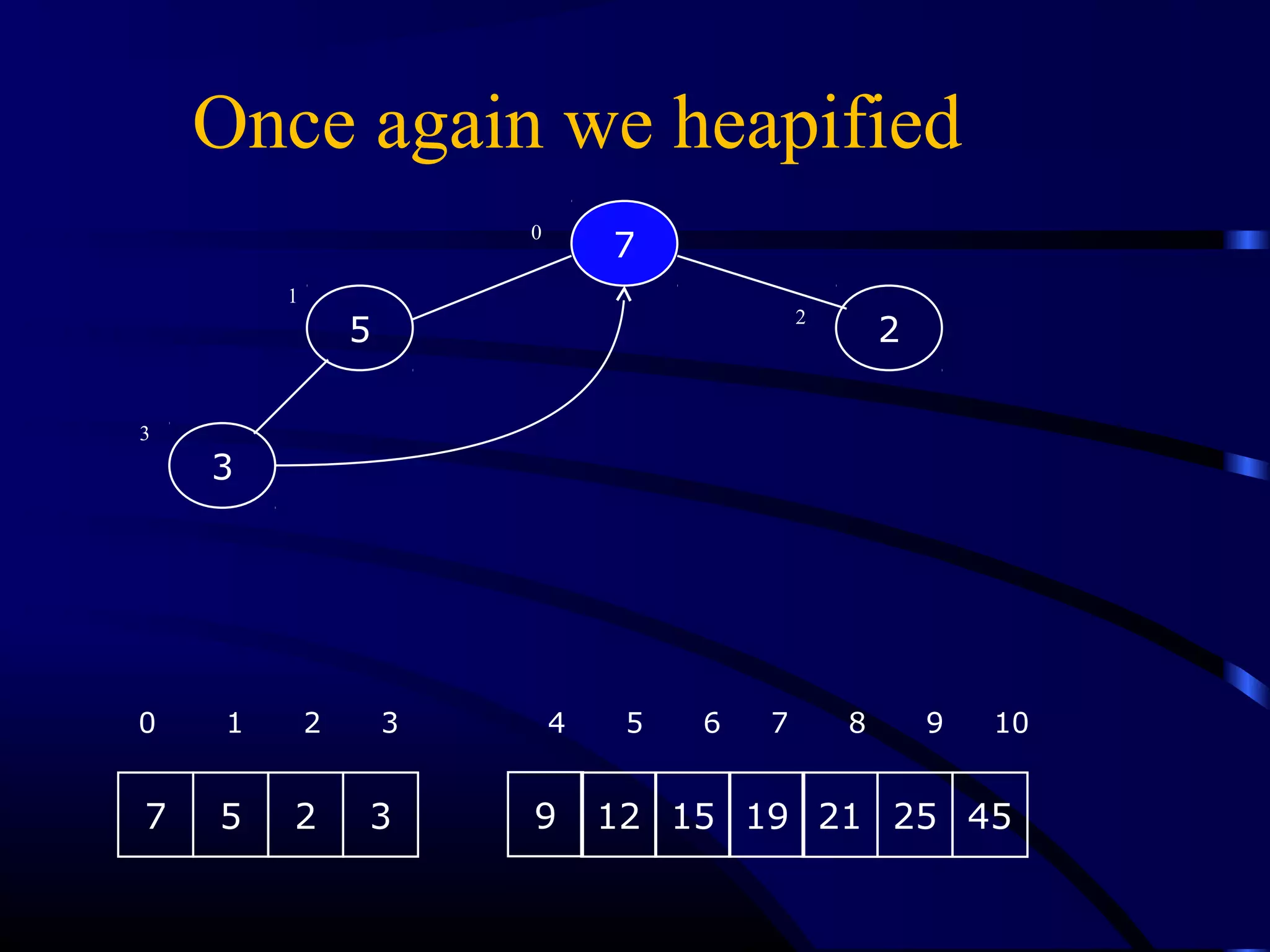
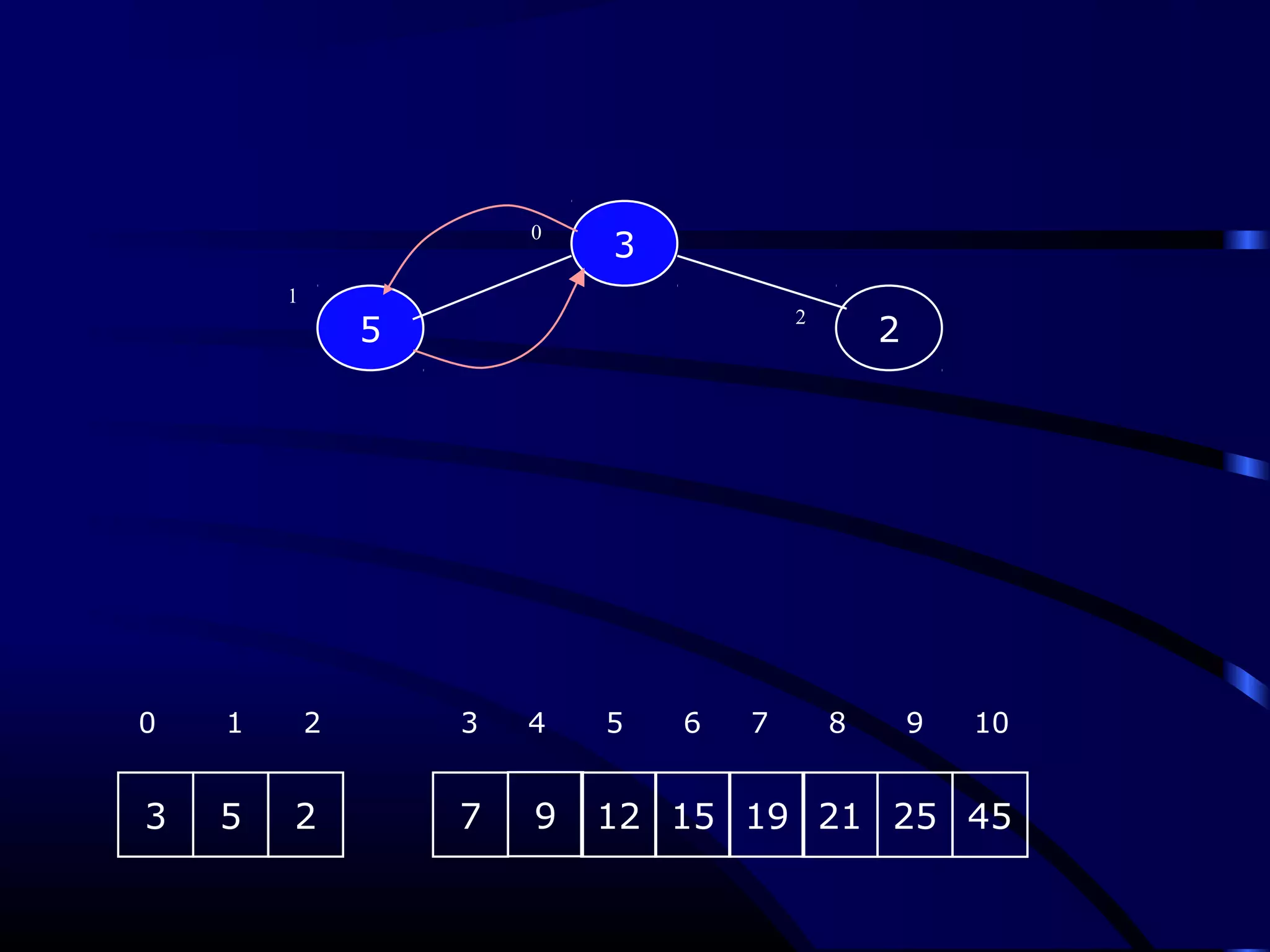
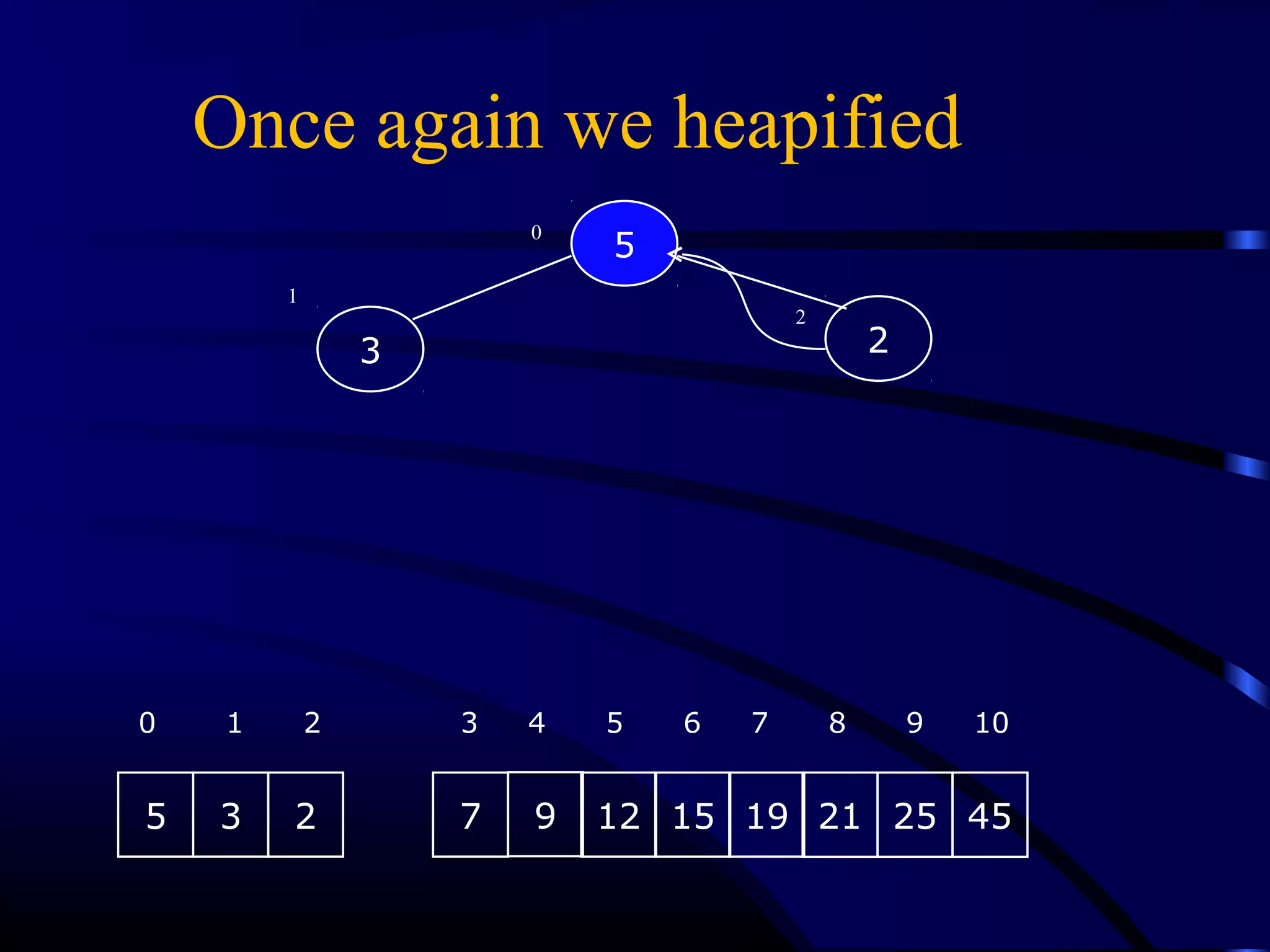
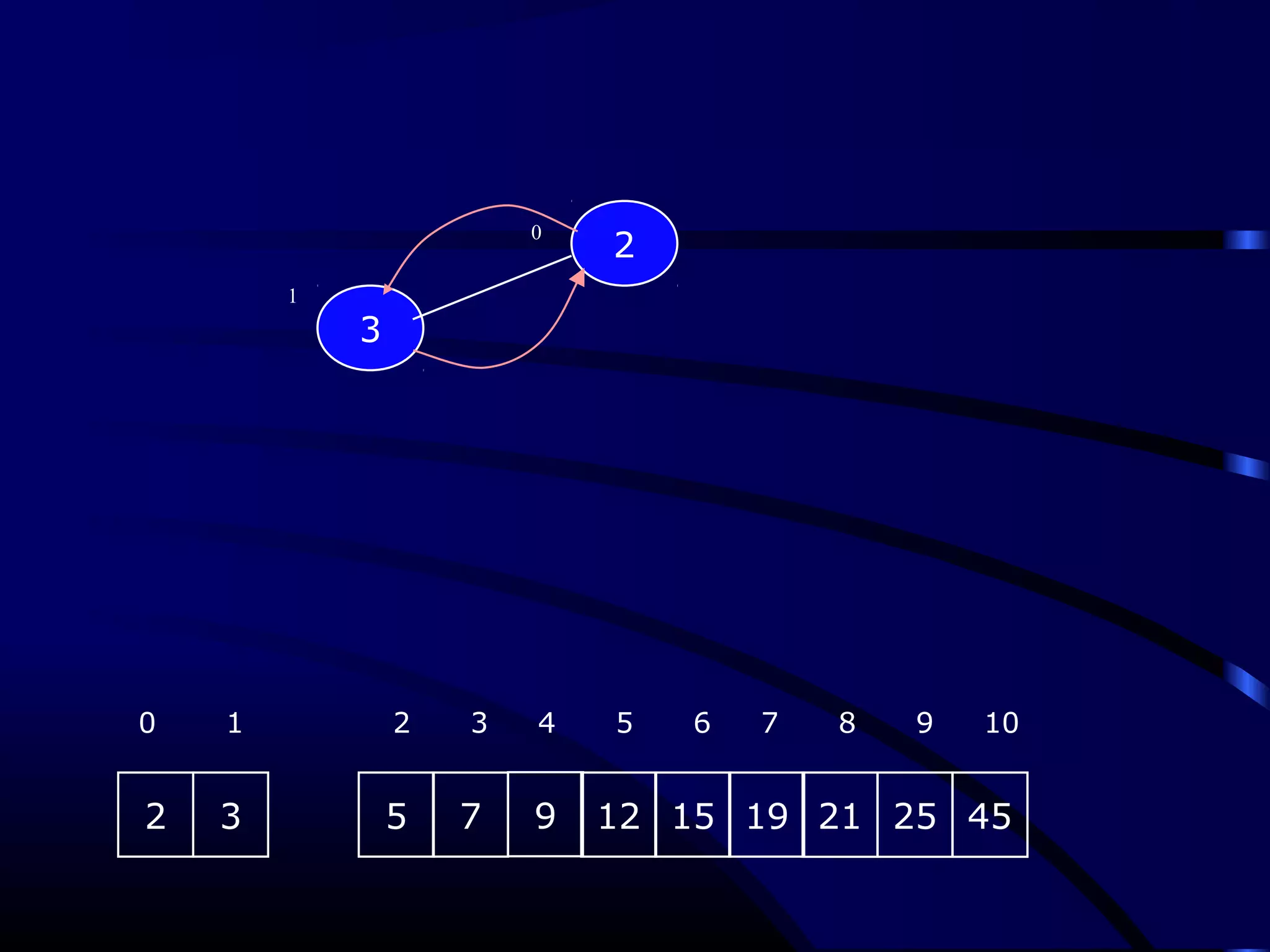
Heapsort is an O(n log n) sorting algorithm that uses a heap data structure. It works by first converting the input array into a max heap, where the largest element is stored at the root. It then repeatedly removes the largest element from the heap and inserts it into the sorted end of the array. This process continues until the heap is empty, resulting in a fully sorted array. The document provides detailed explanations and examples of how to construct a max heap from an array and how to remove and re-heapify elements during the sorting process.

1. Heapsort

2. Why we study Heapsort?
• It is a well-known, traditional sorting
algorithm you will be expected to know
• Heapsort is always O(n log n)
– Quicksort is usually O(n log n) but in the worst
case slows to O(n2
)
– Quicksort is generally faster, but Heapsort is
better in time-critical applications
• Heapsort have really cool algorithm!

3. What is a “heap”?
• Definitions of heap:
1. A large area of memory from which the
programmer can allocate blocks as needed, and
deallocate them (for ex:“new and delete”) when
no longer needed
2. A balanced, left-justified binary tree in which
no node has a value greater than the value in its
parent(heap property)
• These two definitions have little in common
• Heapsort uses the second definition

4. Binary Tree
Typical example for binary tree
Remember:
The depth of a node is its distance from the root
The depth of a tree is the depth of the deepest node
Depth,of tree ,
h=log2(n)
no: of nodes,
n=2h+1
-1
n=15,h=3
0
3
2
1
root
back

5. Balanced binary trees
• A binary tree of depth n is balanced if all the
nodes at depths 0 through n-2 have two children
Balanced Balanced Not balanced
n-2
n-1
n
back

6. Left-justified binary trees
• A balanced binary tree is left-justified if:
– all the leaves are at the same depth, or
– all the leaves at depth n+1 are to the left of all
the nodes at depth n
(nodes must be filled from left)
Left-justified
Not left-justified left-justified

7. The heap property
• A node has the heap property if the value in the
node is as large as or larger than the values in its
children
• A binary tree is a heap if all nodes in it have the
heap property
12
8 3
Blue node has
heap property
12
8 12
Blue node has
heap property
12
8 14
Blue node does not
have heap property

8. SiftUp
• If a node does not have heap property,
you can give it the heap property by exchanging its value
with the value of the larger child
• This is sometimes called sifting up
• Notice that the child may have lost the heap property
14
8 12
Blue node has
heap property
12
8 14
Blue node does not
have heap property

9. Constructing a heap
• A tree consisting of a single node is automatically
a heap
• We construct a heap by adding nodes one at a
time:
– Add the node just to the left of the leftmost node in the
deepest level
– If the deepest level is full, start a new level
• Examples: Add a new
node here
Add a new
node here

10. Before turn on to sorting
Remember
Sift up=Trickle down
Array Binary tree
Binary tree Heapifying Heap
Heap must be always balanced &
left justified
For a heap largest value will be in the
root

11. Sorting
• What do heaps have to do with sorting an array?
• The answer is:
– Because the binary tree is balanced and left justified, it
can be represented as an array
– All our operations on binary trees can be represented as
operations on arrays
– To sort:
heapify the array;
while the array isn’t empty {
remove and replace the root;
re-heap the new root node;
}

12. 21 15 25 3 5 12 7 19 45 2 9
0 1 2 3 4 5 6 7 8 9 10
Mapping an array into Binary tree
• Notice:
– The left child of index i is at index 2*i+1
– The right child of index i is at index 2*i+2
– Example: the children of node 3 (3) are 7 (19) and 8 (45)
3
4519
5
2
12
9
7
21
2515
0
1
2
3
4 5 6
7 8 9 10

13. Heapify the Binary tree
3
4519
5
2
12
9
7
21
2515
21 15 25 3 5 12 7 19 45 2 9
0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4 5 6
7 8 9 10

14. Heapify the Binary tree
3
4519
5
2
12
9
7
21
2515
21 15 25 3 5 12 7 19 45 2 9
0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4 5 6
7 8 9 10

15. Heapify the Binary tree
9
519
3
2
12
45
7
21
2515
21 15 25 3 9 12 7 19 45 2 5
0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4 5 6
7 8 9 10

16. Heapify the Binary tree
9
519
15
2
1245 7
21
25
3
21 15 25 45 9 12 7 19 3 2 5
0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4 5 6
7 8 9 10

17. Heapify the Binary tree
9
5
45
15
2
12
19
7
21
25
3
21 45 25 15 9 12 7 19 3 2 5
0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4 5 6
7 8 9 10

18. Heapify the Binary tree
9
515
21
2
12
45
719
25
3
21 45 25 19 9 12 7 15 3 2 5
0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4 5 6
7 8 9 10

19. We Heapified the Binary tree
9
515
45
2
12
21
719
25
3
45 21 25 19 9 12 7 15 3 2 5
0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4 5 6
7 8 9 10
largest

20. step 2: Removing the root
• Recall that the largest number is now in the root
• Suppose we discard the root:
• How can we fix the binary tree so it is once again balanced
and left-justified?
• Solution: remove the rightmost leaf at the deepest level
and use it for the new root
19
315
9
2
12
5
7
45
2521
0
1
2
3
4 5 6
7 8 9 10

21. Removing and replacing the root
• The “root” is the first element in the array
• The “rightmost node at the deepest level” is the last
element
• Swap them...
• ...And pretend that the last element in the array no longer
exists—that is, the “last index” is 9 (2)
45 21 25 19 9 12 7 15 3 2 5
0 1 2 3 4 5 6 7 8 9 10
5 21 25 19 9 12 7 15 3 2 45
0 1 2 3 4 5 6 7 8 9 10

22. 9
15
5
2
12
25
719
21
3
0
1
2
3 4 5 6
7 8 9
The reHeap method I
• Our tree is balanced and left-justified, but no longer a heap
• However, only the root lacks the heap property
• We can siftUp() the root
• After doing this, one and only one of its children may have
lost the heap property
5 21 25 19 9 12 7 15 3 2 45
0 1 2 3 4 5 6 7 8 9 10

23. The reHeap method II
• Now the left child of the root (still the number 5) lacks the
heap property
9
15
12
2
25
5
719
21
3
0
1
2
3 4 5 6
7 8 9
25 21 5 19 9 12 7 15 3 2 45
0 1 2 3 4 5 6 7 8 9 10

24. Heap again…..
• Our tree is once again a heap, because every node in it has
the heap property
• Once again, the largest (or a largest) value is in the root
• We can repeat this process until the tree becomes empty
• This produces a sequence of values in order largest to smallest
9
15
12
2
25
5
719
21
3
0
1
2
3 4 5 6
7 8 9

25. reHeap method
• Now the left child of the root (still the number 2) lacks the
heap property
9
15
21
5
2
719
12
3
0
1
2
3 4 5 6
7 8
2 21 5 19 9 12 7 15 3 25 45
0 1 2 3 4 5 6 7 8 9 10

26. 9
15
2
519 7
21
12
3
0
1
2
3 4 5 6
7 8
21 2 12 19 9 5 7 15 3 25 45
0 1 2 3 4 5 6 7 8 9 10

27. 9
19
15
52 7
21
12
3
0
1
2
3
4 5 6
7 8
21 2 12 19 9 5 7 15 3 25 45
0 1 2 3 4 5 6 7 8 9 10

28. 9
2
19
515 7
21
12
0
1
2
3 4 5 6
7 8
21 19 12 15 9 5 7 2 3 25 45
0 1 2 3 4 5 6 7 8 9 10
Once again we heapified
3

29. 9
2
19
5
3
7
12
15
0
1
2
3
4 5 6
7 8
3 19 12 15 9 12 7 2
0 1 2 3 4 5 6 7 8 9 10
21 25 45

30. 9
2
15 5
3
7
12
19
0
1
2
3
4 5 6
7 8
19 3 12 15 9 12 7 2
0 1 2 3 4 5 6 7 8 9 10
21 25 45

31. 9
2
3 5
15
7
12
19
0
1
2
3
4 5 6
7 8
21 25 45
Once again we heapified
19 15 12 3 9 12 7 2
0 1 2 3 4 5 6 7 8 9 10

32. 93
15
5
2
7
12
0
1
2
3
4 5 6
2 15 12 3 9 12 7 19
0 1 2 3 4 5 6 7 8 9 10
21 25 45

33. 3
15
9 5
2
7
12
0
1
2
3
4 5 6
15 2 12 3 9 12 7 19
0 1 2 3 4 5 6 7 8 9 10
21 25 45

34. 23 5
9
7
12
15
0
1
2
3
4 5 6
Once again we heapified
15 9 12 3 2 5 7 19
0 1 2 3 4 5 6 7 8 9 10
21 25 45

35. 2
7
5
12
3
9
0
1
2
3
4 5
7 9 12 3 2 5 15 19
0 1 2 3 4 5 6 7 8 9 10
21 25 45

36. 2
12
5
9
3
7
0
1
2
3
4 5
12 9 7 3 2 5 15 19
0 1 2 3 4 5 6 7 8 9 10
21 25 45
Once again we heapified

37. 2
5
79
3
0
1
2
3
4
5 9 12 3 7 12 15 19
0 1 2 3 4 5 6 7 8 9 10
21 25 45

38. 2
5 7
9
3
0
1
2
3
4
9 5 12 3 7 12 15 19
0 1 2 3 4 5 6 7 8 9 10
21 25 45
Once again we heapified

39. 2
5 7
3
0
1
2
3
2 5 7 3 9 12 15 19
0 1 2 3 4 5 6 7 8 9 10
21 25 45

40. 7
5 2
3
0
1
2
3
7 5 2 3 9 12 15 19
0 1 2 3 4 5 6 7 8 9 10
21 25 45
Once again we heapified

41. 3
25
0
1
2
3 5 2 7 9 12 15 19
0 1 2 3 4 5 6 7 8 9 10
21 25 45

42. 5
3 2
0
1
2
5 3 2 7 9 12 15 19
0 1 2 3 4 5 6 7 8 9 10
21 25 45
Once again we heapified

43. 2
3
0
1
2 3 5 7 9 12 15 19
0 1 2 3 4 5 6 7 8 9 10
21 25 45

44. 3
2
0
1
3 2 5 7 9 12 15 19
0 1 2 3 4 5 6 7 8 9 10
21 25 45
Once again we heapified

45. 2
2
0
3 5 7 9 12 15 19
1 2 3 4 5 6 7 8 9 10
21 25 45
0
2 3 5 7 9 12 15 19 21 25 45
0 1 2 3 4 5 6 7 8 9 10

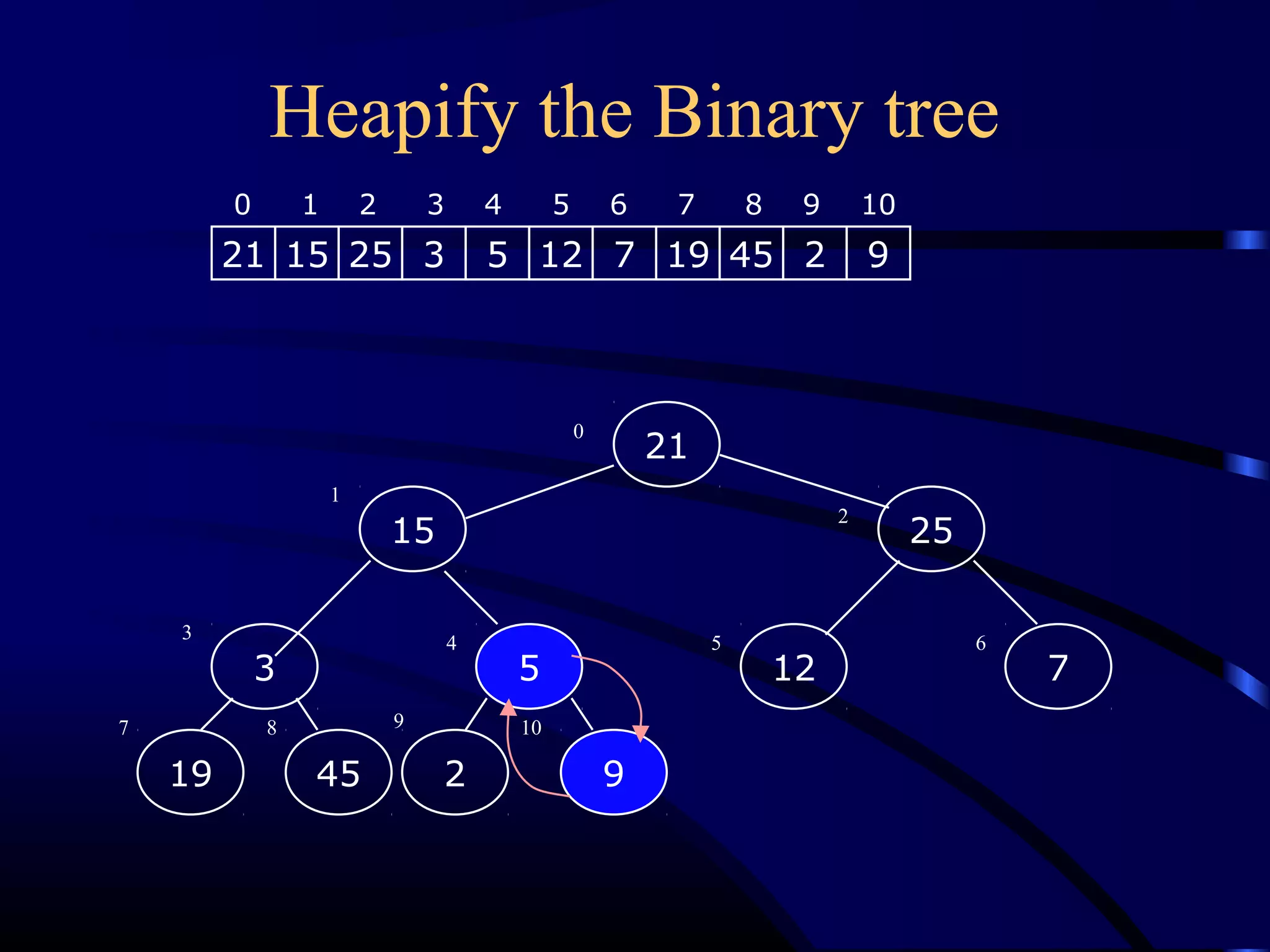
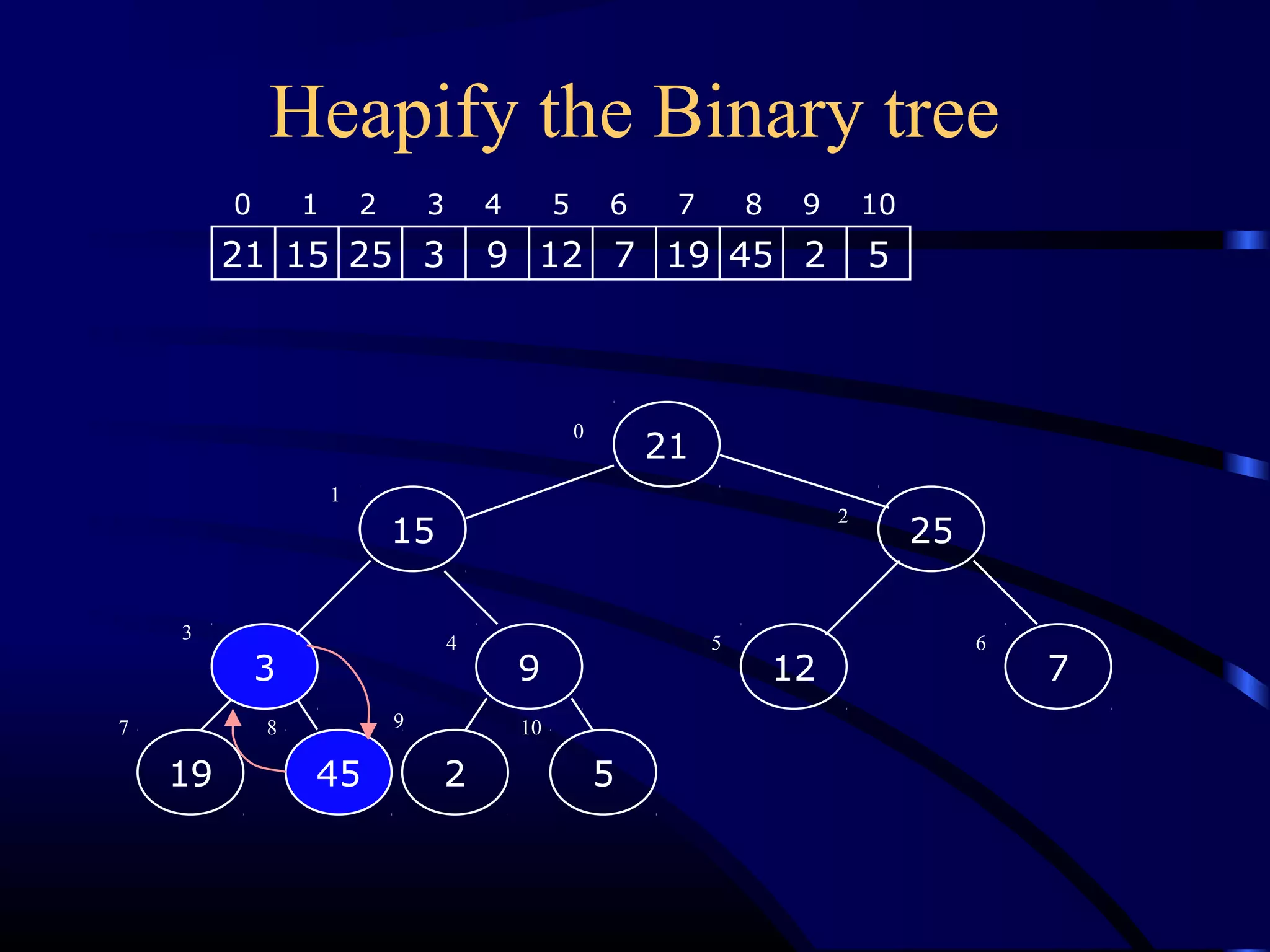
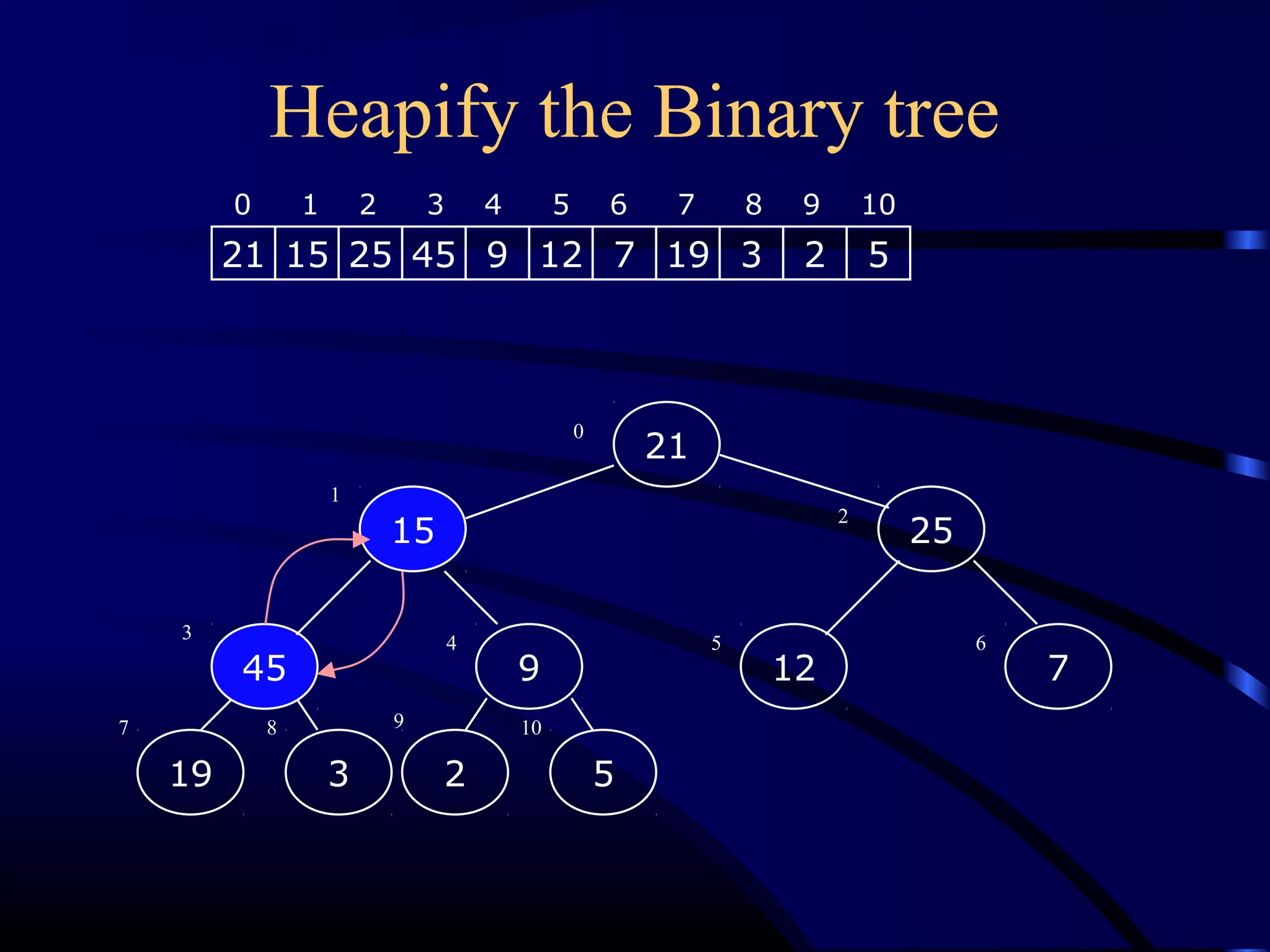
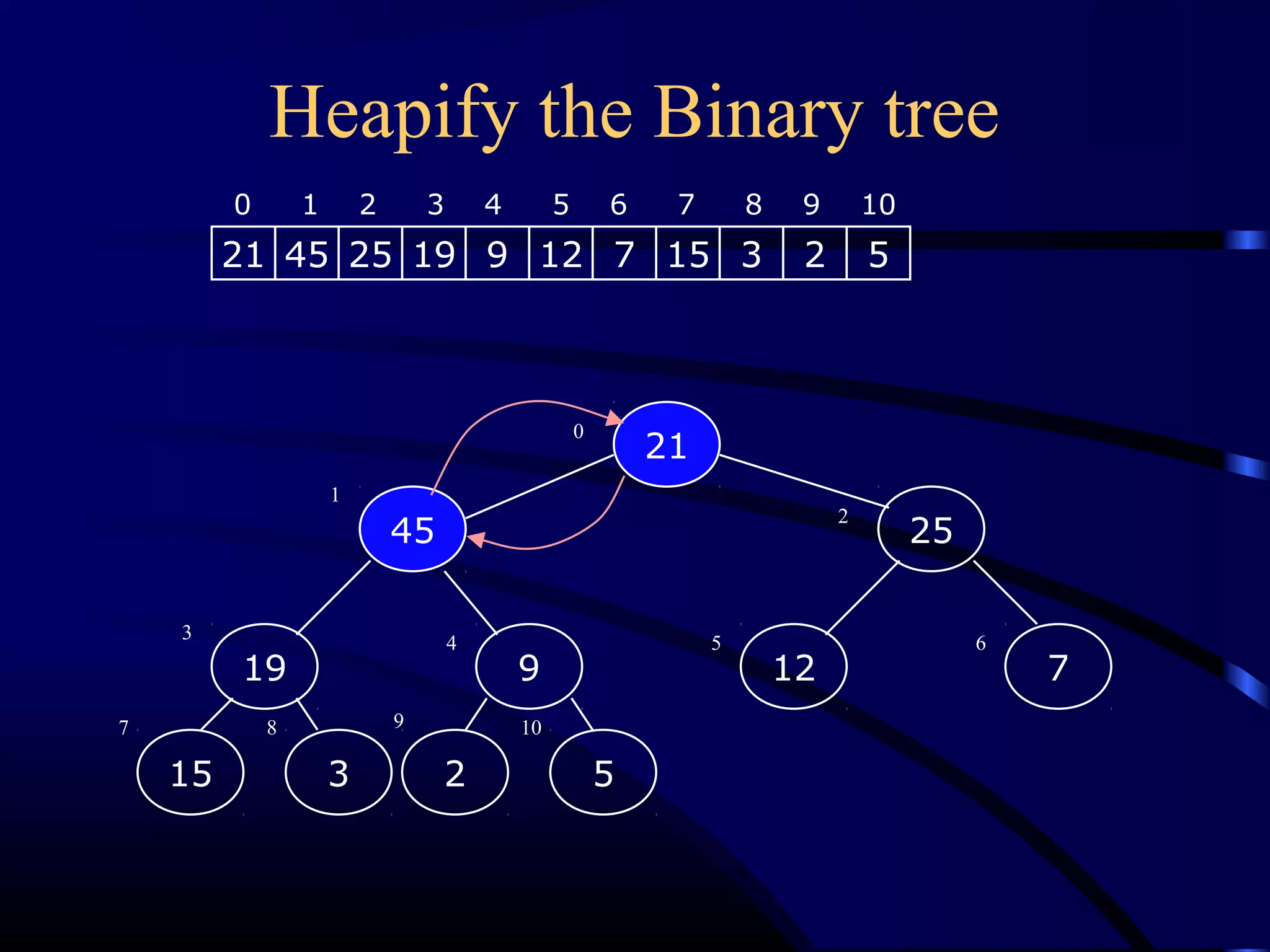
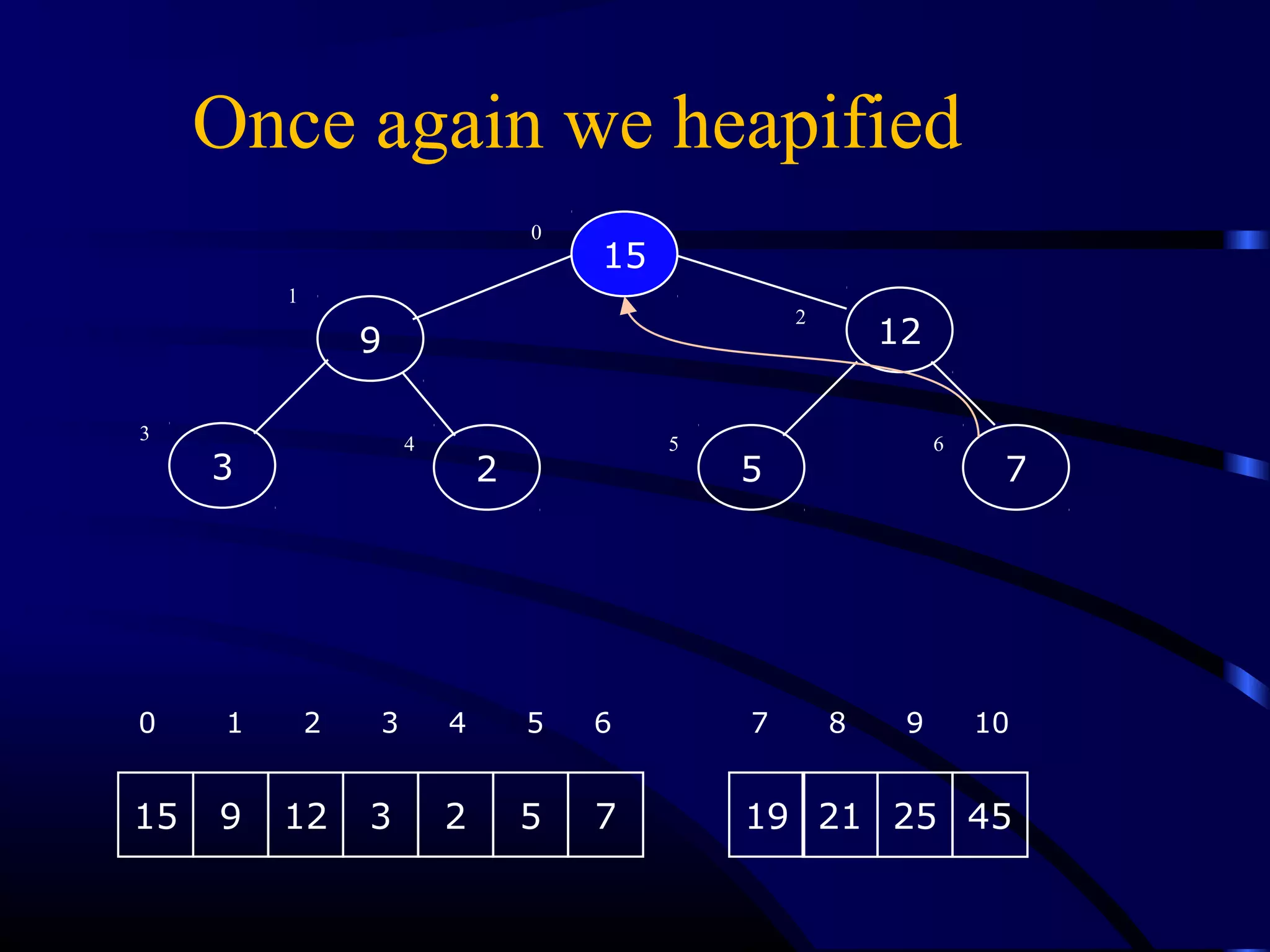
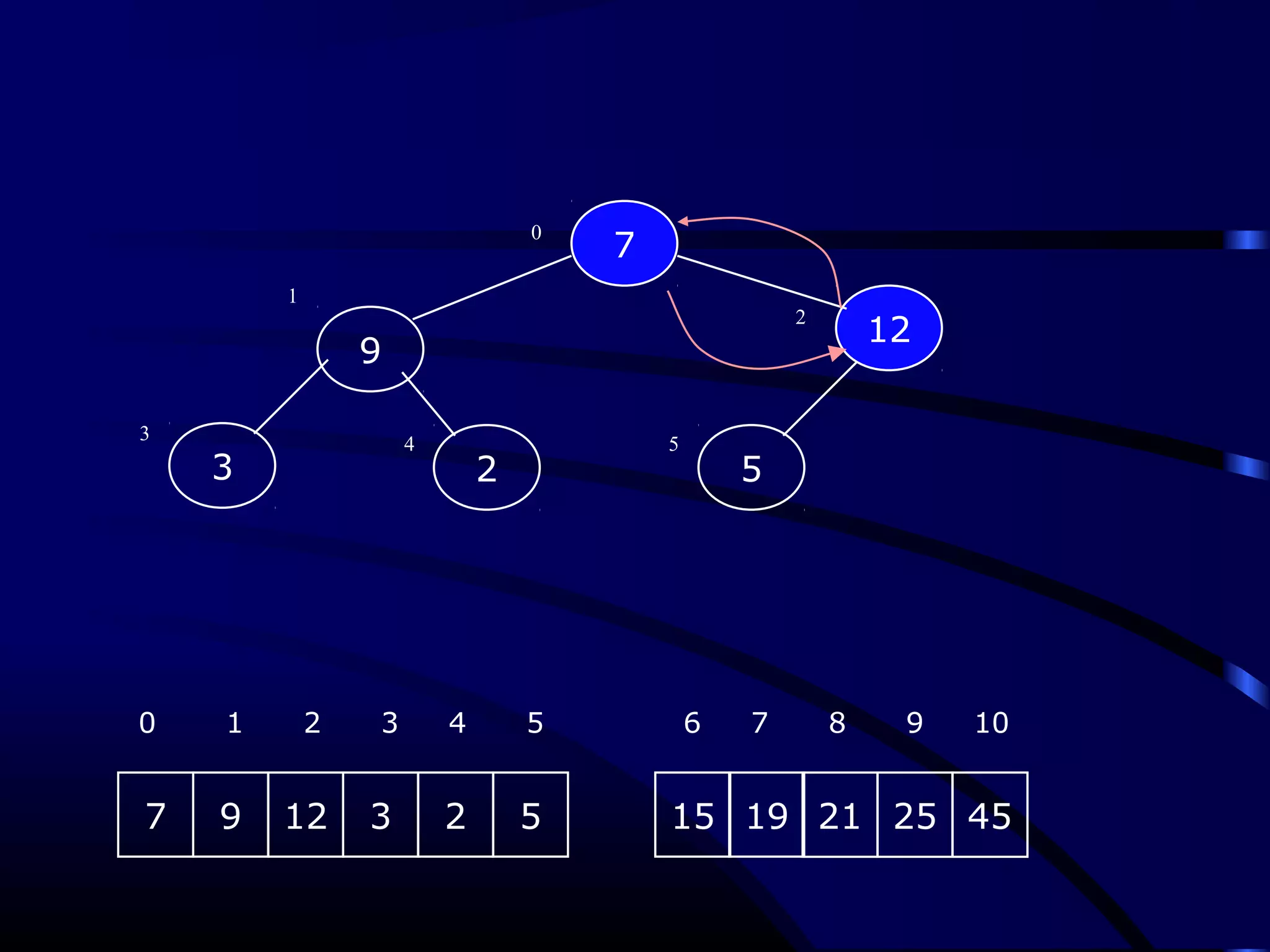
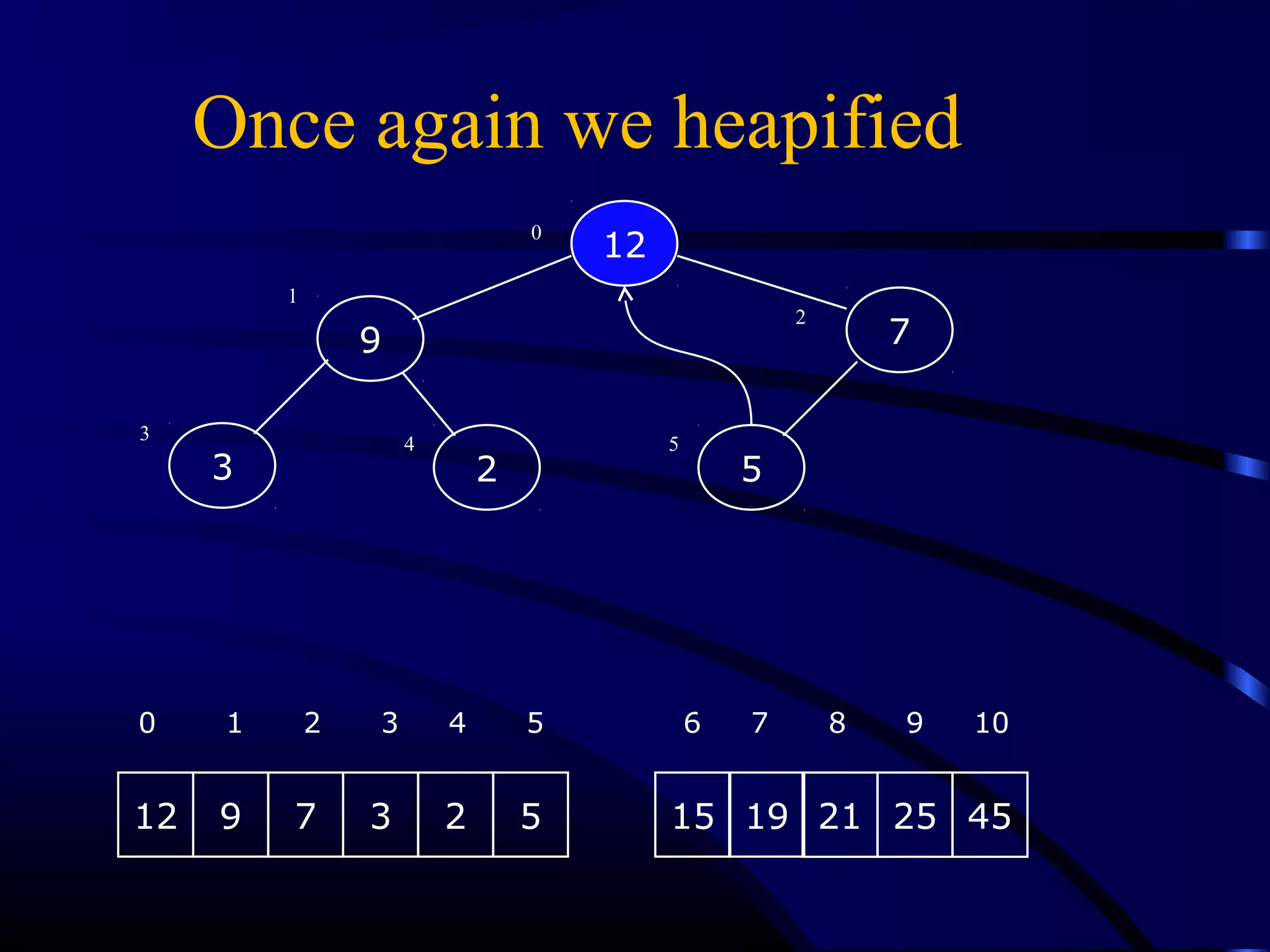
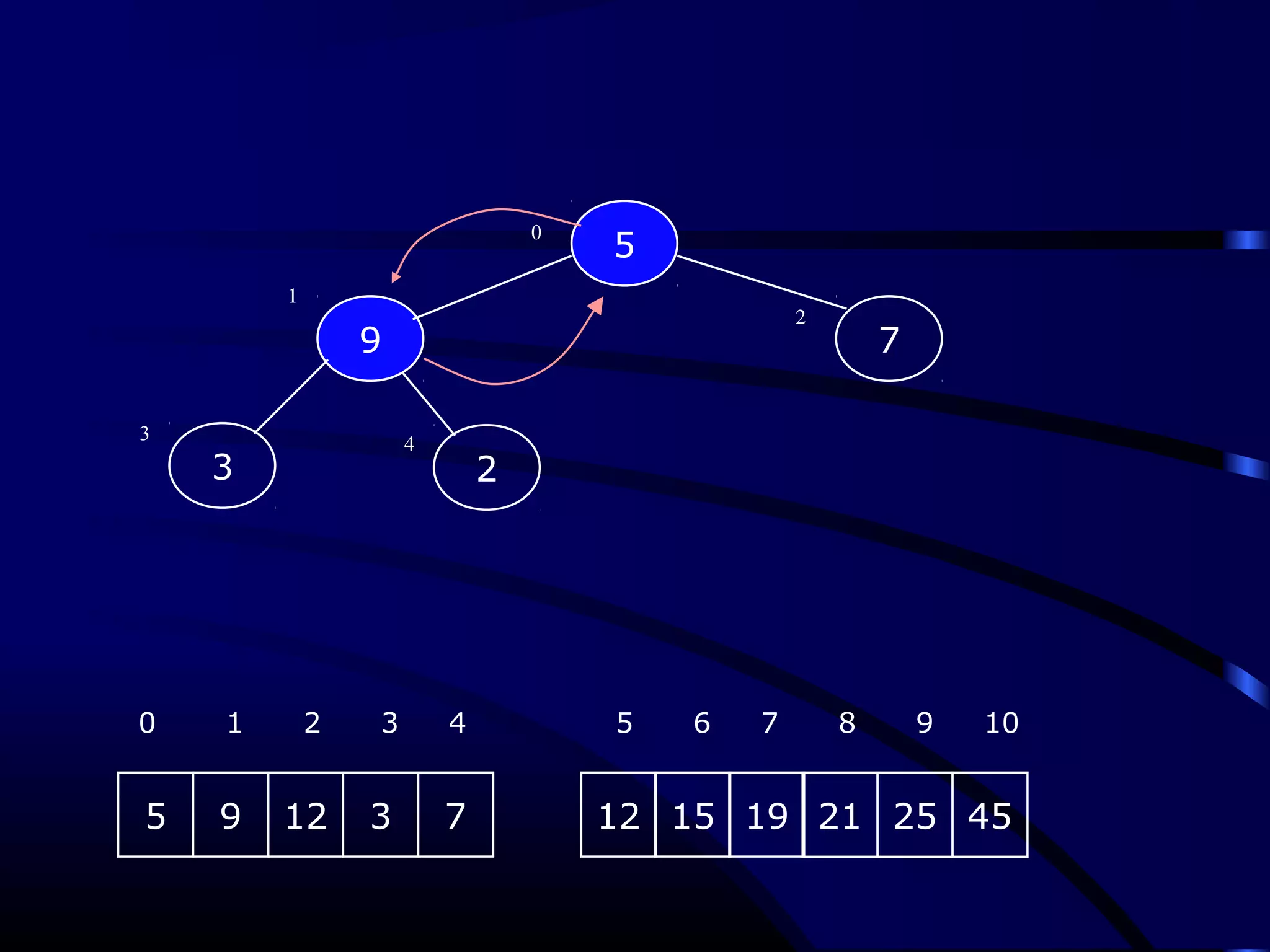
46. Heapify (Heapify (AA,, ii))
1. l ← left [i]
2. r ← right [i]
3. if l ≤ heap-size [A] and A[l] > A[i]
4. then largest ← l
5. else largest ← i
6. if r ≤ heap-size [A] and A[i] > A[largest]
7. then largest ← r
8. if largest ≠ i
9. then exchange A[i] ↔ A[largest]
10. Heapify (A, largest)

47. Void CreateHeap(int arr[],int size)
{ int i,father,son;
for(i=1;i<size;i++)
{ int element=arr[i];
son=i;
father=floor(son/2);
while((son>0)&&(arr[father]<element))
{ arr[son]=arr[father];
son=father;
father=floor(son/2);
} arr[son]=element;
}
CODE 4 HEAPIFYING

48. Heap sort make 2 standard heap
operations: insertion & root deletion.
We delete the maximum,We delete the maximum,
Swap it with the last elementSwap it with the last element
Pretend that the last element in the array no longer existsPretend that the last element in the array no longer exists
ThenThen
Sort root of the heap.Sort root of the heap.
Heapify the remaining binary tree.Heapify the remaining binary tree.
Repeat it until the tree became emptyRepeat it until the tree became empty

49. void root_deletion( )
{
for ( int i = count - 1 ; i > 0 ; i-- )
{
int temp = arr[i] ;last value
arr[i] = arr[0] ;passing the root value
arr[0]=temp;
makeheap(i);
}
}
Root deletion program
implementation

50. Analysis I
• Here’s how the algorithm starts:
heapify the array;
• Heapifying the array: we compare each of n
nodes
– Each node has to be sifted up, possibly as far as
the root
• Since the binary tree is perfectly balanced,
sifting up a single node takes O(log n)
time
– Since we do this n times, heapifying takes
n*O(log n) time, that is, O(n log n) time

51. Analysis II
• Here’s the rest of the algorithm:
while the array isn’t empty {
remove and replace the root;
reheap the new root node;
}
• We do the while loop n times (actually, n-1 times),
because we remove one of the n nodes each time
• Removing and replacing the root takes O(1) time
• Therefore, the total time is n times however long it
takes the reheap method

52. Analysis III
• To reheap the root node, we have to follow one
path from the root to a leaf node (and we might
stop before we reach a leaf)
• The binary tree is perfectly balanced
• Therefore, this path is O(log n) long
– And we only do O(1) operations at each node
– Therefore, reheaping takes O(log n) times
• Since we reheap inside a while loop that we do n
times, the total time for the while loop is
n*O(log n), or O(n log n)

53. Analysis IV
• Here’s the algorithm again:
heapify the array;
while the array isn’t empty {
remove and replace the root;
reheap the new root node;
}
• We have seen that heapifying takes O(n log n) time
• The while loop takes O(n log n) time
• The total time is therefore O(n log n) + O(n log n)
• This is the same as O(n log n) time

54. The End

56. Jinsha
Jinsha
M
idhun
M
idhun
Navya
Navya
Remesha
Remesha
Shybin
Shybin

58. WelcomeWelcome
JinshaJinsha
MidhunMidhun
NavyaNavya
Remesha
Remesha
ShybinShybin