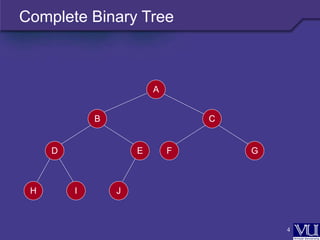
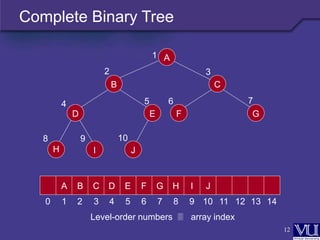
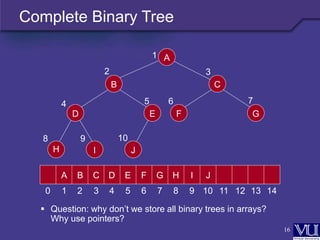
- A complete binary tree is a tree that is completely filled, with the possible exception of the bottom level, which is filled from left to right.
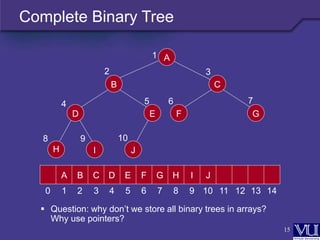
- Such a tree can be stored efficiently in an array, with the left and right children and parent of each node calculable from its array position.
- A heap is a complete binary tree that follows the heap property - a parent node's key is always greater than or equal to its children's keys. Heaps allow efficient insertion and deletion of minimum/maximum elements.