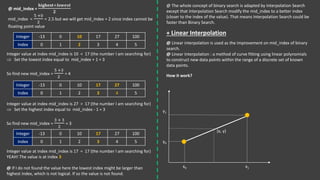
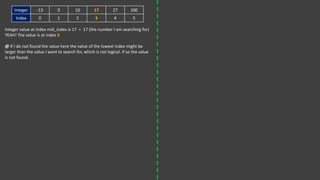
Interpolation search is an algorithm for searching sorted arrays that estimates the position of the search key. It improves on binary search by using linear interpolation to calculate a mid-point index closer to where the key may be found. Linear interpolation uses the difference between two known data points to estimate a value between them. Interpolation search first calculates a mid-point index based on the key's value relative to the array's minimum and maximum. It then adjusts the search range based on comparing the key to the value at the mid-point before recalculating a new mid-point. This allows it to potentially find the key in fewer comparisons than binary search, with a time complexity of O(log log n).

1. Interpolation Search
By: 3Algo

2. Interpolation ?
@ Interpolation (mathematic) : a type of estimation , a method of
constructing new data points within the range of a discrete set of known
data points.
Interpolation Search ?
@ Interpolation Search : An algorithm for searching for a key in an array that
has been ordered (sorted) by numerical values assigned to the key (key
values). It was first described by W.W Peterson in 1957.
### HAPPY NOTE ### : “Interpolation Search” is very similar to “Binary
Search” but it could be much faster since it could estimate the closest or
might be the right index of the “KEY”, that we want to search for.
Story Begin
To completely understand about the “Interpolation Search”, here are the
topics to learn.
+ Binary Search
+ Linear Interpolation
+ Interpolation Search
+ Binary Search
@ Both “Binary Search” and “Interpolation Search” only work with sorted
array of values because it does not know where to search if the array is not
sorted.
@ The expected result from the search algorithm is FOUND or NOT FOUND
@ Time Complexity of Binary Search : log2 (n)
How it work?
Example: I have a sorted array (ascending) of integer like this
-13, 0, 10, 17, 27, 100
Let find index of number “17”
Solution:
Integer -13 0 10 17 27 100
Index 0 1 2 3 4 5
Step to find it:
1. Find middle index of the array if the lowest index is less than or equal to
highest index otherwise => Ops! Not found
2. Compare the value of the middle index
| if it is equal to the number I am searching for => Yeah! I found it
| if it is less than the number I am searching for => It might be in the
higher index so set my smallest index = the middle index + 1; then redo it
from step one
| if it is higher than the number I am searching for => set highest index =
the middle index -1; then redo

3. Integer -13 0 10 17 27 100
Index 0 1 2 3 4 5
@ mid_index =
𝐡𝐢𝐠𝐡𝐞𝐬𝐭+𝒍𝒐𝒘𝒆𝒔𝒕
𝟐
mid_index =
5 +0
2
= 2.5 but we will get mid_index = 2 since index cannot be
floating point value
Integer value at index mid_index is 10 < 17 (the number I am searching for)
 Set the lowest index equal to mid_index + 1 = 3
So find new mid_index =
5 +3
2
= 4
Integer -13 0 10 17 27 100
Index 0 1 2 3 4 5
Integer value at index mid_index is 27 > 17 (the number I am searching for)
 Set the highest index equal to mid_index - 1 = 3
So find new mid_index =
3 + 3
2
= 3
Integer -13 0 10 17 27 100
Index 0 1 2 3 4 5
Integer value at index mid_index is 17 = 17 (the number I am searching for)
YEAH! The value is at index 3
@ If I do not found the value here the lowest index might be larger than
highest index, which is not logical. If so the value is not found.
@ The whole concept of binary search is adapted by Interpolation Search
except that Interpolation Search modify the mid_index to a better index
(closer to the index of the value). That means Interpolation Search could be
faster than Binary Search.
+ Linear Interpolation
@ Linear interpolation is used as the improvement on mid_index of binary
search.
@ Linear Interpolation : a method of curve fitting using linear polynomials
to construct new data points within the range of a discrete set of known
data points.
How it work?
(x, y)
x0 x1
y0
y1

4. @ The graph means that it has 2 known points and I want to estimate
another point by assume the value is linear. So the value I want to find is
somewhere between the two known points.
@ From the point that I want to find to point 0 (x0, y0) and to point 1 (x1, y1)
is a the same line so the slope of the two line is the same or equal.
y − y0
x −x0
=
y1− y0
x1− x0
Let say I want to find the “x” when I know “y”
 x = x0 + (x1 – x0) ×
y− y0
y1− y0
@ This interpolation formula will be used in the interpolation search to find
a better mid_index.
+ Interpolation Search
@ The expected result from the search algorithm is FOUND or NOT FOUND
@ Time Complexity of Binary Search : O (log log n))
Since the improvement in on mid_index, so the better mid_index is
mid_index =
lowest + (highest – lowest) ×
integer I am searching −lowest interger
highest integer −lowest interger
How it work?
Example: I have a sorted array (ascending) of integer like this
-13, 0, 10, 17, 27, 100
Let find index of number “17” now using interpolation search instead of
binary search
Solution:
Integer -13 0 10 17 27 100
Index 0 1 2 3 4 5
mid_index = 0 + (5 – 0)
17 −(−13)
100 −(−13)
= 1.32743363 but we will get
mid_index = 1 since index cannot be floating point value
Integer value at index mid_index is 0 < 17 Set the lowest index equal to
mid_index + 1 = 2
So find new mid_index = 2 + (5 – 2)
17 − 0
100 − 0
= 2.51 so take mid_index = 2
Integer -13 0 10 17 27 100
Index 0 1 2 3 4 5
Integer value at index mid_index is 10 < 17 Set the lowest index equal to
mid_index + 1 = 3
So find new mid_index = 3 + (5 – 3)
17 −10
100 −10
= 3.15151515 so take
mid_index = 3

5. Integer -13 0 10 17 27 100
Index 0 1 2 3 4 5
Integer value at index mid_index is 17 = 17 (the number I am searching for)
YEAH! The value is at index 3
@ If I do not found the value here the value of the lowest index might be
larger than the value I want to search for, which is not logical. If so the value
is not found.

6. Reading Materials
• https://en.wikipedia.org/wiki/Interpolation
• https://en.wikipedia.org/wiki/Linear_interpolation
• https://en.wikipedia.org/wiki/Binary_search_algorithm