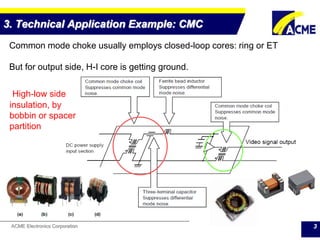
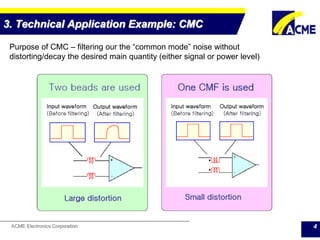
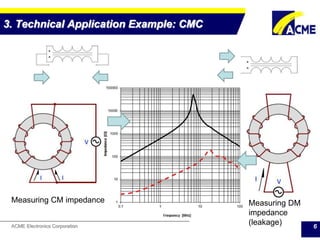
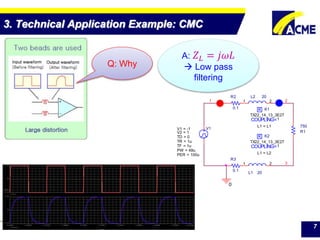
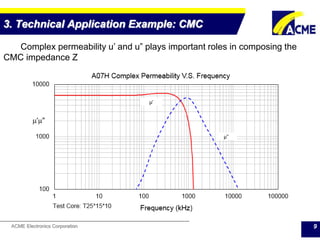
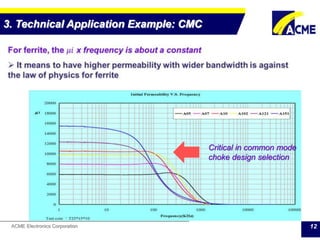
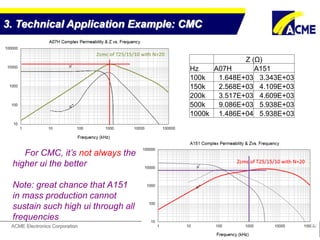
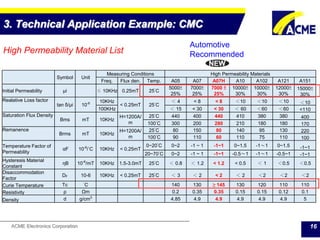
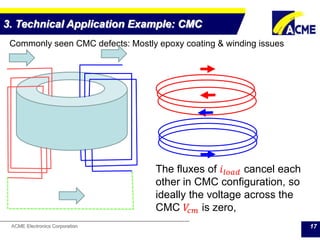
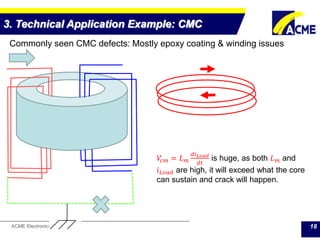
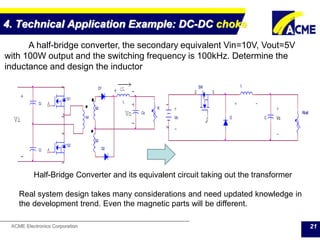
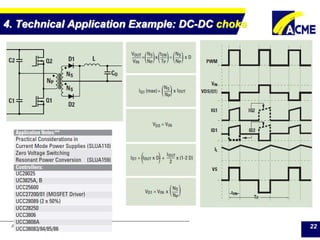
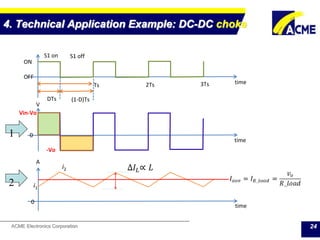
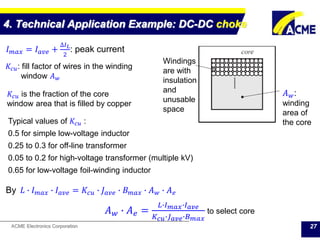
The document summarizes technical applications of ferrites, including common mode chokes and DC-DC chokes. It describes how common mode chokes use ferrite cores to filter out common mode noise without affecting the main signal or power. It also explains how to design an inductor for a DC-DC converter circuit based on specifications like output voltage, current, and allowed voltage variation. The document provides examples of ferrite material properties and considerations for designing chokes and inductors to meet power requirements while avoiding saturation or overheating of the ferrite core.