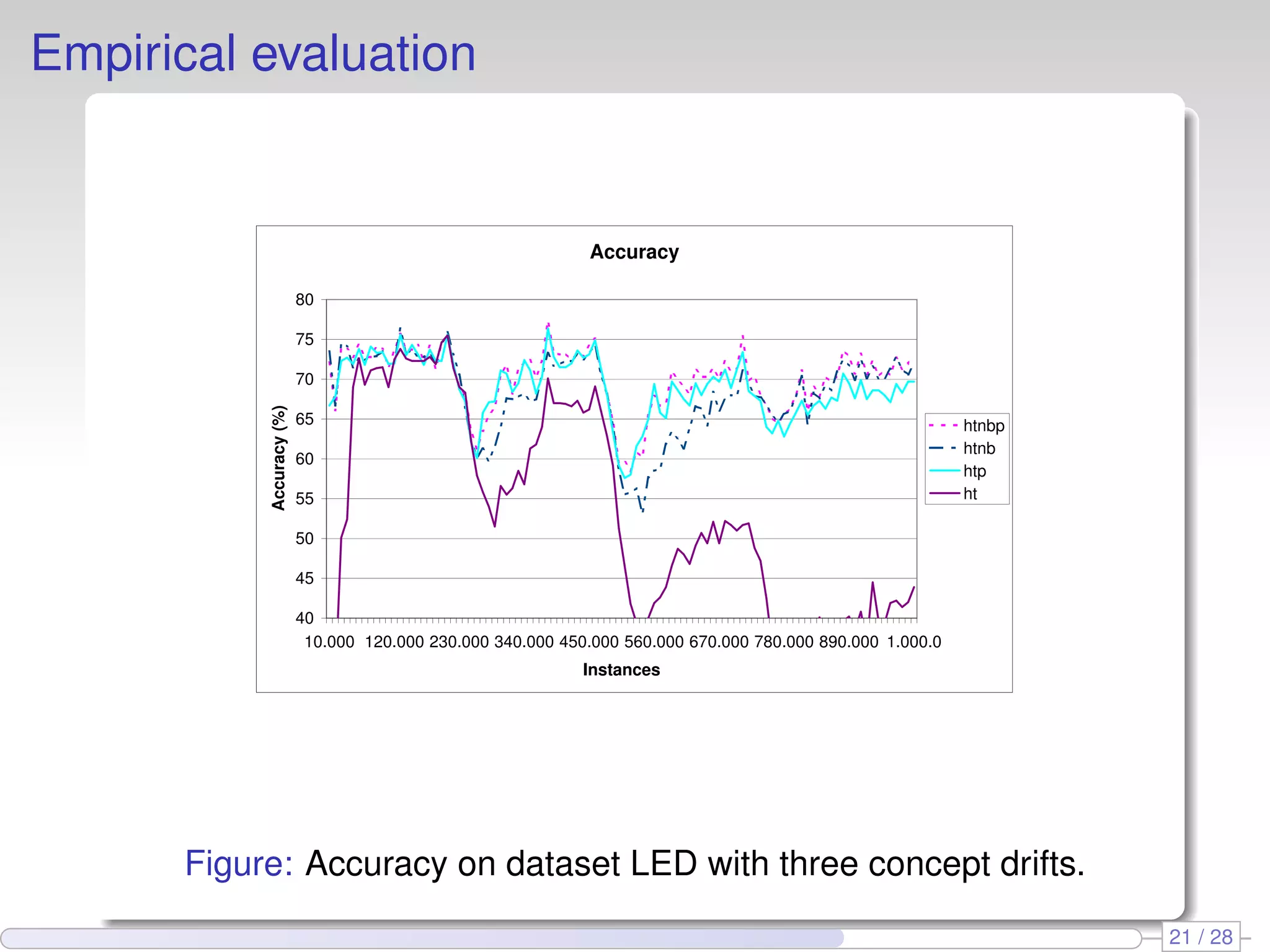
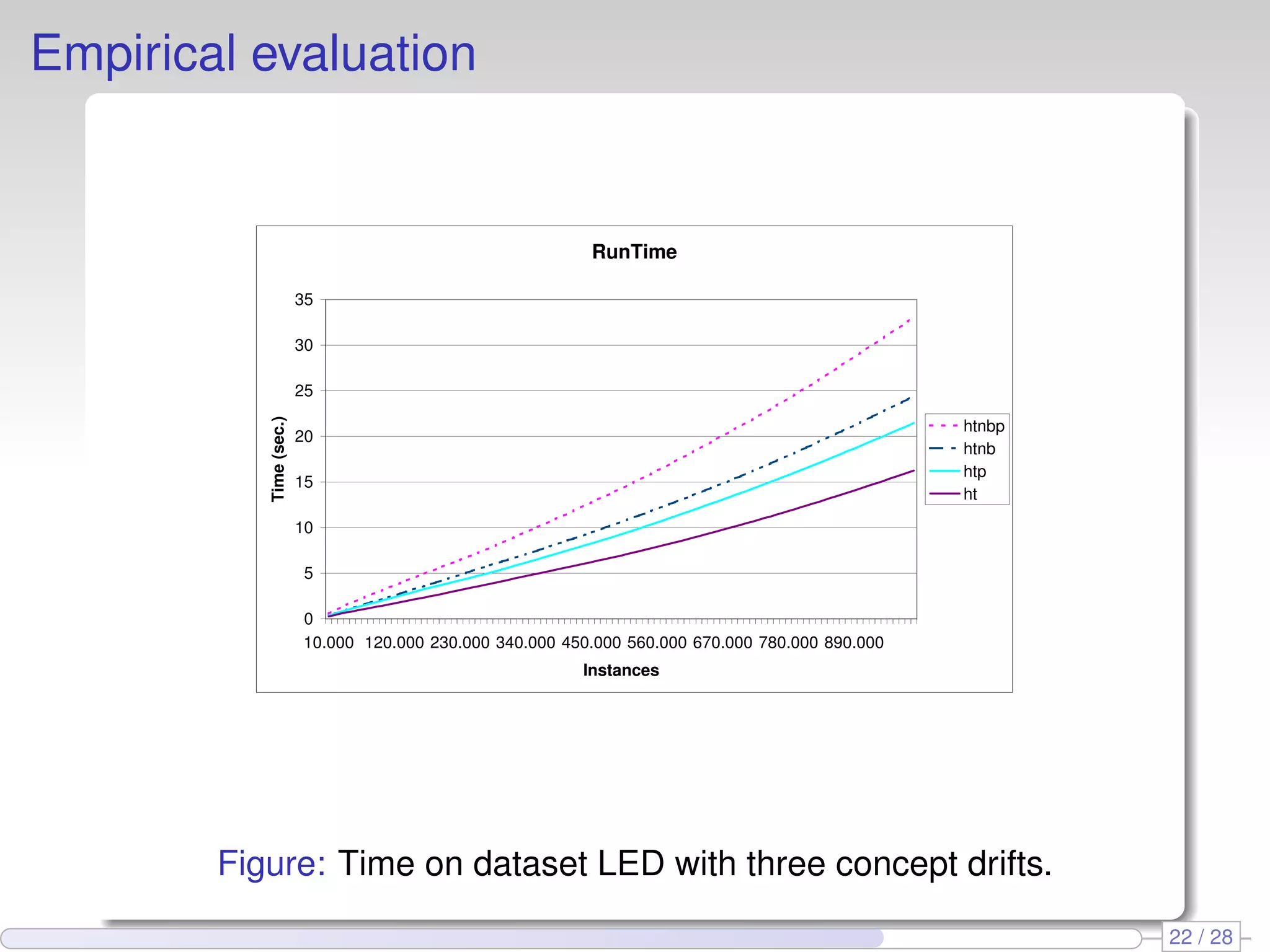
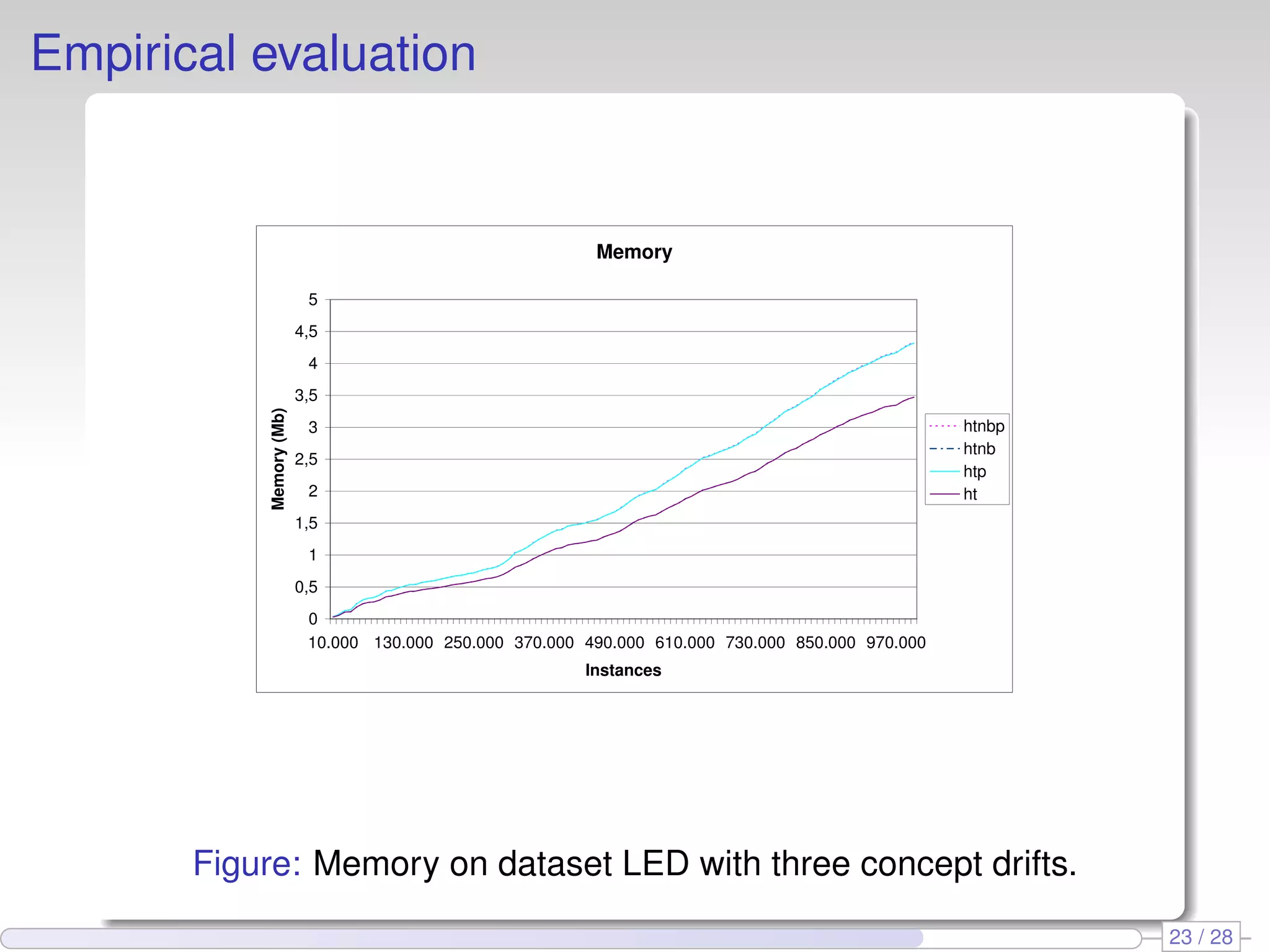
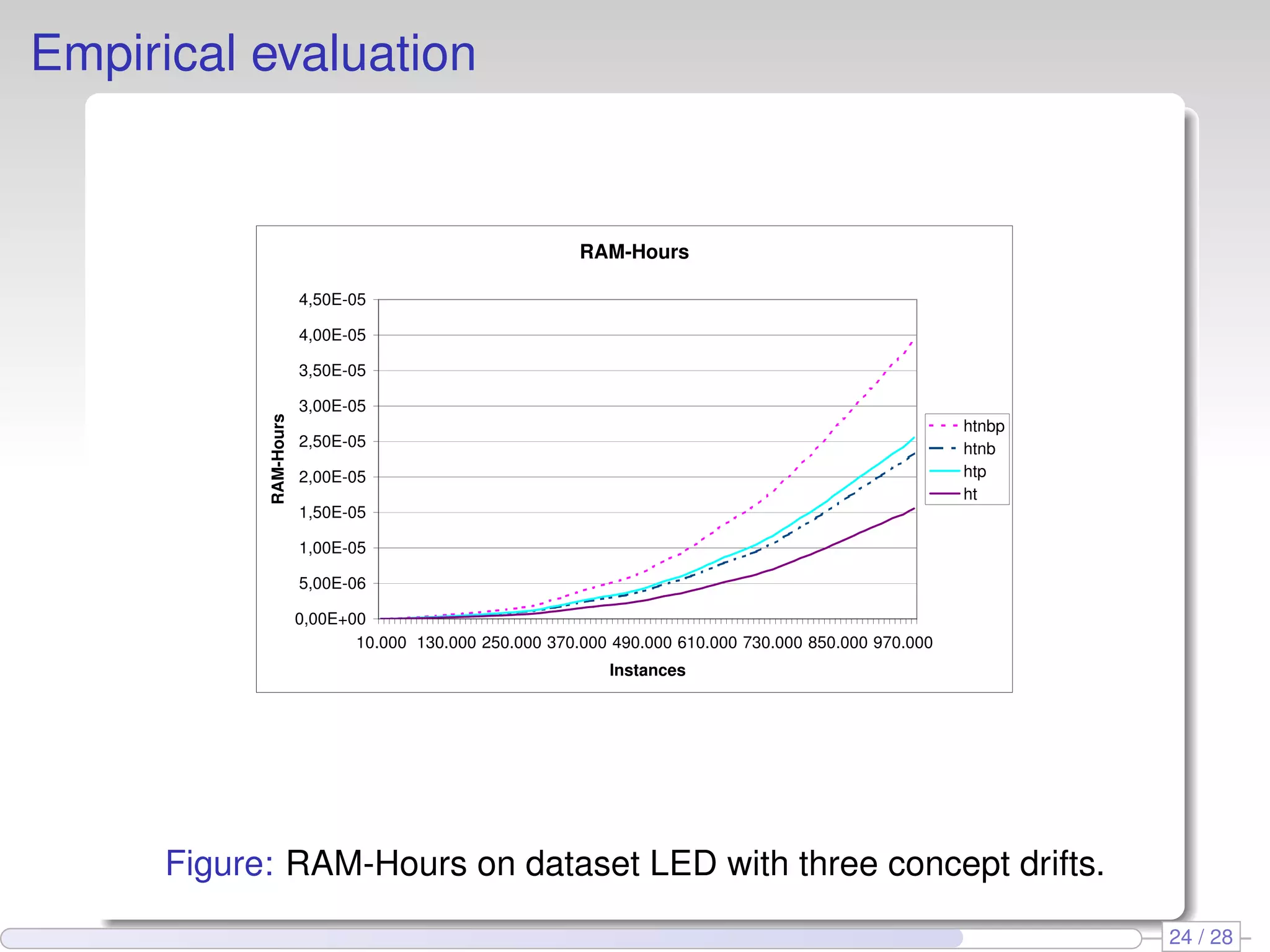
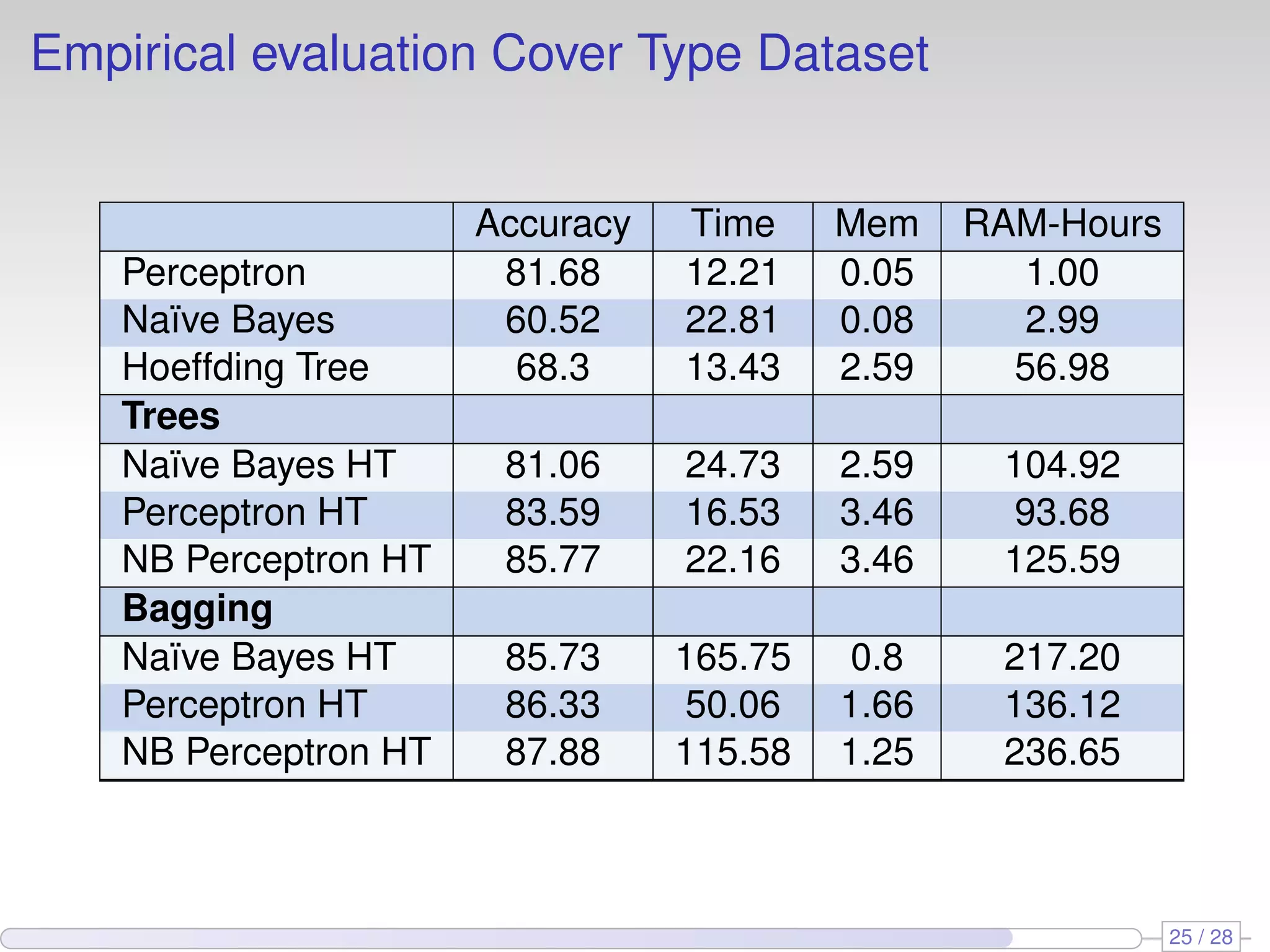
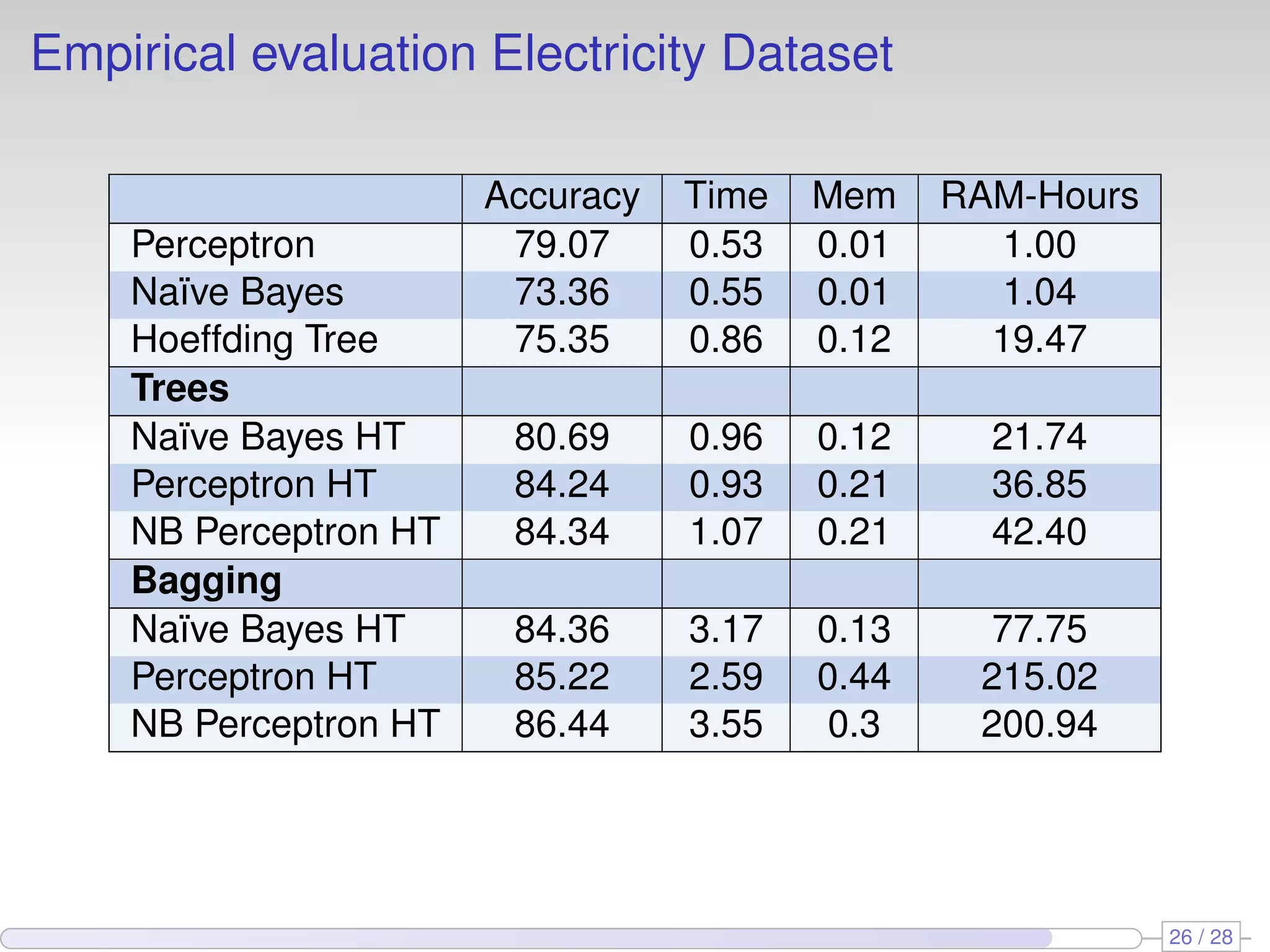
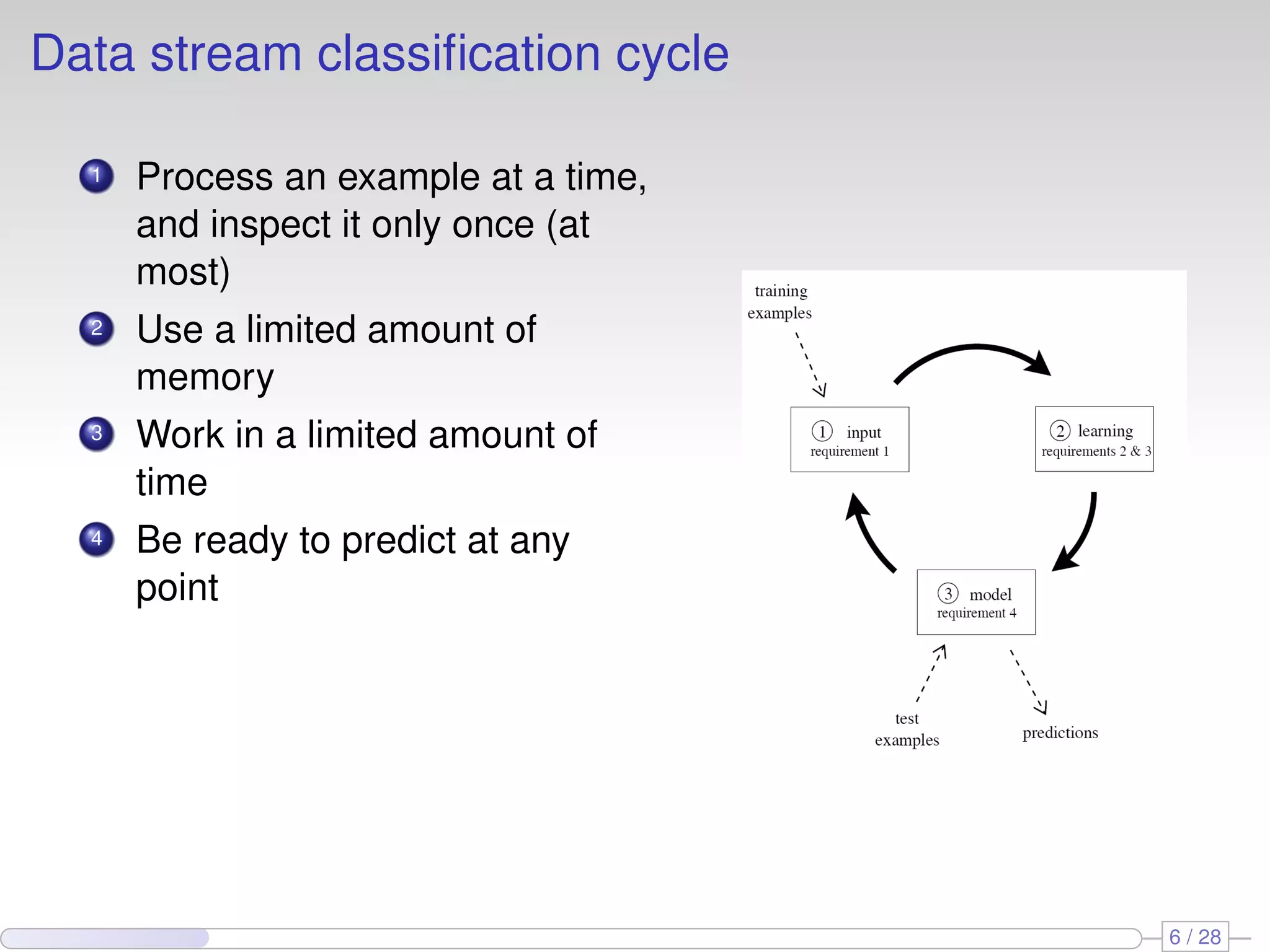
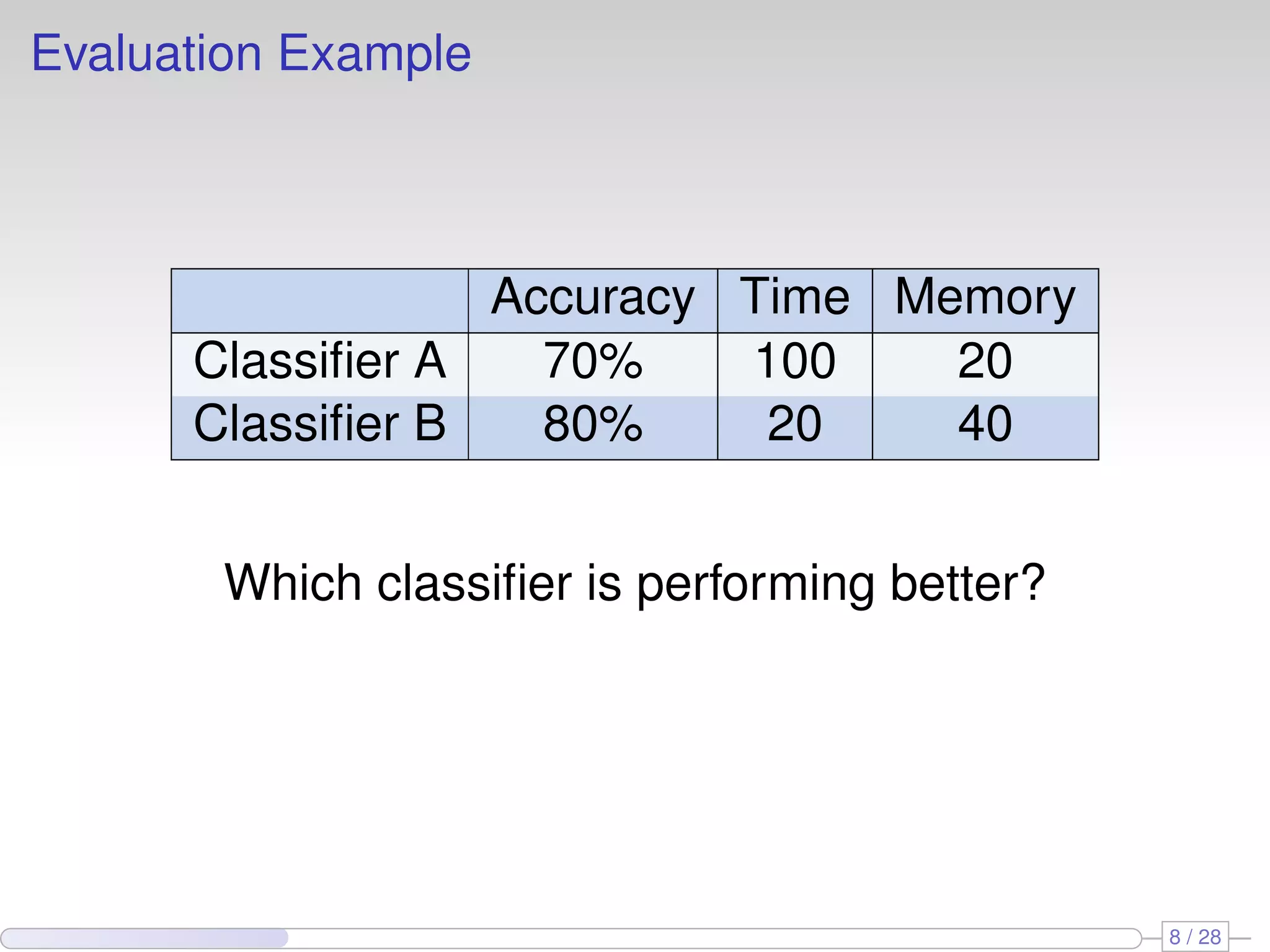
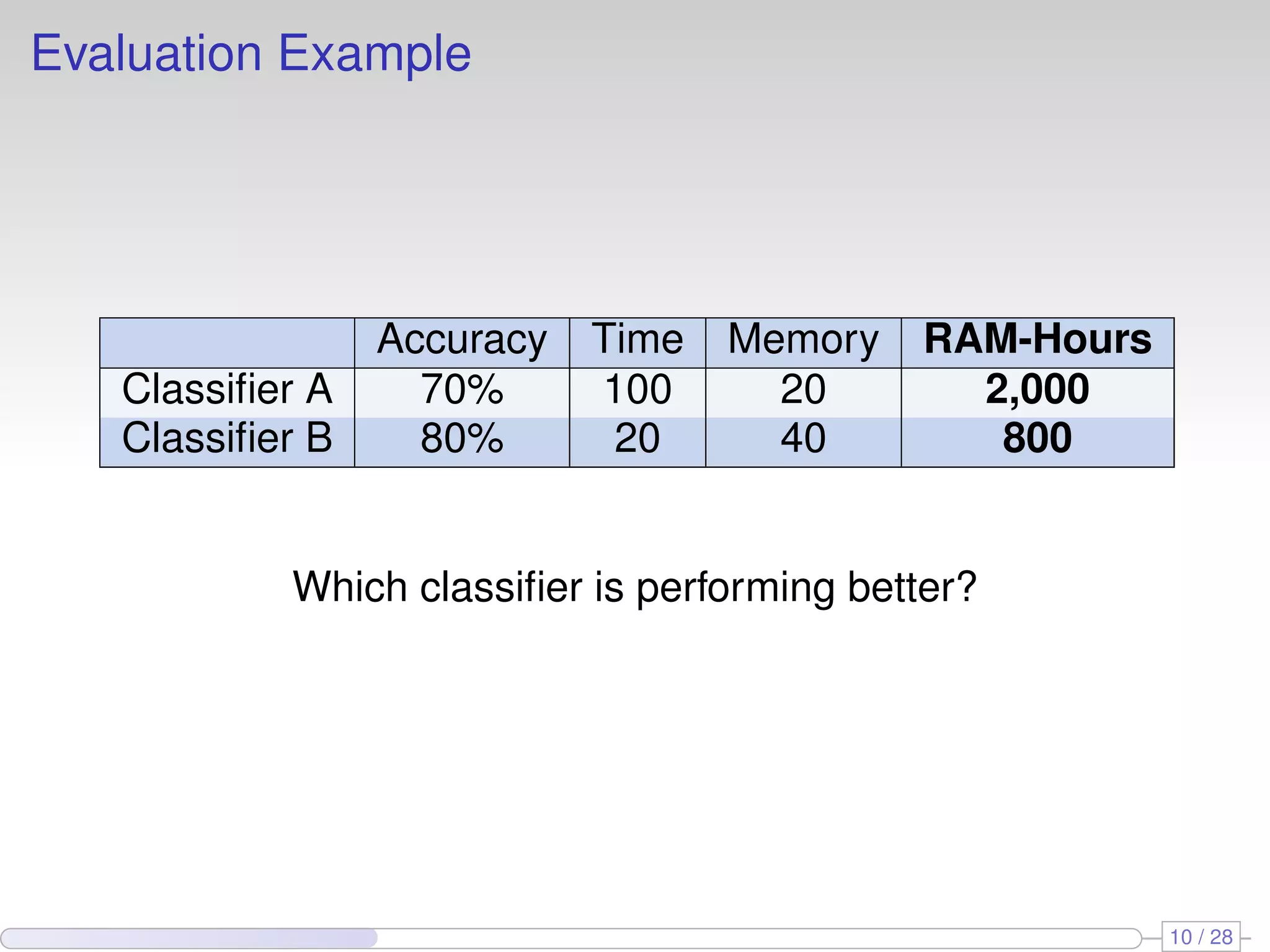
The document proposes using perceptron learners at the leaves of Hoeffding decision trees to improve performance on data streams. It introduces a new evaluation metric called RAM-Hours that considers both time and memory usage. The authors empirically evaluate different classifier models, including Hoeffding trees with perceptron and naive Bayes learners at leaves, on several datasets. Results show that hybrid models like Hoeffding naive Bayes perceptron trees often provide the best balance of accuracy, time and memory usage.

1. Fast Perceptron Decision Tree Learning
from Evolving Data Streams
Albert Bifet, Geoff Holmes, Bernhard Pfahringer, and Eibe Frank
University of Waikato
Hamilton, New Zealand
Hyderabad, 23 June 2010
14th Pacific-Asia Conference on Knowledge Discovery and Data Mining
(PAKDD’10)

2. Motivation
RAM Hours
Time and Memory in one measure
Hoeffding Decision Trees with Perceptron Learners at
leaves
Improve performance of classification methods for data
streams
2 / 28

3. Outline
1 RAM-Hours
2 Perceptron Decision Tree Learning
3 Empirical evaluation
3 / 28

4. Mining Massive Data
2007
Digital Universe: 281 exabytes (billion gigabytes)
The amount of information created exceeded available
storage for the first time
Web 2.0
106 million registered users
600 million search queries per day
3 billion requests a day via its API.
4 / 28

5. Green Computing
Green Computing
Study and practice of using computing resources efficiently.
Algorithmic Efficiency
A main approach of Green Computing
Data Streams
Fast methods without storing all dataset in memory
5 / 28

6. Data stream classification cycle
1 Process an example at a time,
and inspect it only once (at
most)
2 Use a limited amount of
memory
3 Work in a limited amount of
time
4 Be ready to predict at any
point
6 / 28

7. Mining Massive Data
Koichi Kawana
Simplicity means the achievement of maximum effect with
minimum means.
time
accuracy
memory
Data Streams
7 / 28

8. Evaluation Example
Accuracy Time Memory
Classifier A 70% 100 20
Classifier B 80% 20 40
Which classifier is performing better?
8 / 28

9. RAM-Hours
RAM-Hour
Every GB of RAM deployed for 1 hour
Cloud Computing Rental Cost Options
9 / 28

10. Evaluation Example
Accuracy Time Memory RAM-Hours
Classifier A 70% 100 20 2,000
Classifier B 80% 20 40 800
Which classifier is performing better?
10 / 28

11. Outline
1 RAM-Hours
2 Perceptron Decision Tree Learning
3 Empirical evaluation
11 / 28

12. Hoeffding Trees
Hoeffding Tree : VFDT
Pedro Domingos and Geoff Hulten.
Mining high-speed data streams. 2000
With high probability, constructs an identical model that a
traditional (greedy) method would learn
With theoretical guarantees on the error rate
Time
Contains “Money”
YES
Yes
NO
No
Day
YES
Night
12 / 28

13. Hoeffding Naive Bayes Tree
Hoeffding Tree
Majority Class learner at leaves
Hoeffding Naive Bayes Tree
G. Holmes, R. Kirkby, and B. Pfahringer.
Stress-testing Hoeffding trees, 2005.
monitors accuracy of a Majority Class learner
monitors accuracy of a Naive Bayes learner
predicts using the most accurate method
13 / 28

14. Perceptron
Attribute 1
Attribute 2
Attribute 3
Attribute 4
Attribute 5
Output hw (xi)
w1
w2
w3
w4
w5
Data stream: xi,yi
Classical perceptron: hw (xi) = sgn(wT xi),
Minimize Mean-square error: J(w) = 1
2 ∑(yi −hw (xi))2
14 / 28

15. Perceptron
Attribute 1
Attribute 2
Attribute 3
Attribute 4
Attribute 5
Output hw (xi)
w1
w2
w3
w4
w5
We use sigmoid function hw = σ(wT x) where
σ(x) = 1/(1+e−x
)
σ (x) = σ(x)(1−σ(x))
14 / 28

16. Perceptron
Minimize Mean-square error: J(w) = 1
2 ∑(yi −hw (xi))2
Stochastic Gradient Descent: w = w +η∇Jxi
Gradient of the error function:
∇J = −∑
i
(yi −hw (xi))∇hw (xi)
∇hw (xi) = hw (xi)(1−hw (xi))
Weight update rule
w = w +η ∑
i
(yi −hw (xi))hw (xi)(1−hw (xi))xi
14 / 28

17. Perceptron
PERCEPTRON LEARNING(Stream,η)
1 for each class
2 do PERCEPTRON LEARNING(Stream,class,η)
PERCEPTRON LEARNING(Stream,class,η)
1 £ Let w0 and w be randomly initialized
2 for each example (x,y) in Stream
3 do if class = y
4 then δ = (1−hw (x))·hw (x)·(1−hw (x))
5 else δ = (0−hw (x))·hw (x)·(1−hw (x))
6 w = w +η ·δ ·x
PERCEPTRON PREDICTION(x)
1 return argmaxclass hwclass
(x)
15 / 28

18. Hybrid Hoeffding Trees
Hoeffding Naive Bayes Tree
Two learners at leaves: Naive Bayes and Majority Class
Hoeffding Perceptron Tree
Two learners at leaves: Perceptron and Majority Class
Hoeffding Naive Bayes Perceptron Tree
Three learners at leaves: Naive Bayes, Perceptron and Majority
Class
16 / 28

19. Outline
1 RAM-Hours
2 Perceptron Decision Tree Learning
3 Empirical evaluation
17 / 28

20. What is MOA?
{M}assive {O}nline {A}nalysis is a framework for online
learning from data streams.
It is closely related to WEKA
It includes a collection of offline and online methods as well
as tools for evaluation:
boosting and bagging
Hoeffding Trees
with and without Na¨ıve Bayes classifiers at the leaves.
18 / 28

21. What is MOA?
Easy to extend
Easy to design and run experiments
Philipp Kranen, Hardy Kremer, Timm Jansen, Thomas
Seidl, Albert Bifet, Geoff Holmes, Bernhard Pfahringer
RWTH Aachen University, University of Waikato
Benchmarking Stream Clustering Algorithms within the
MOA Framework
KDD 2010 Demo
18 / 28

22. MOA: the bird
The Moa (another native NZ bird) is not only flightless, like the
Weka, but also extinct.
19 / 28

23. MOA: the bird
The Moa (another native NZ bird) is not only flightless, like the
Weka, but also extinct.
19 / 28

24. MOA: the bird
The Moa (another native NZ bird) is not only flightless, like the
Weka, but also extinct.
19 / 28

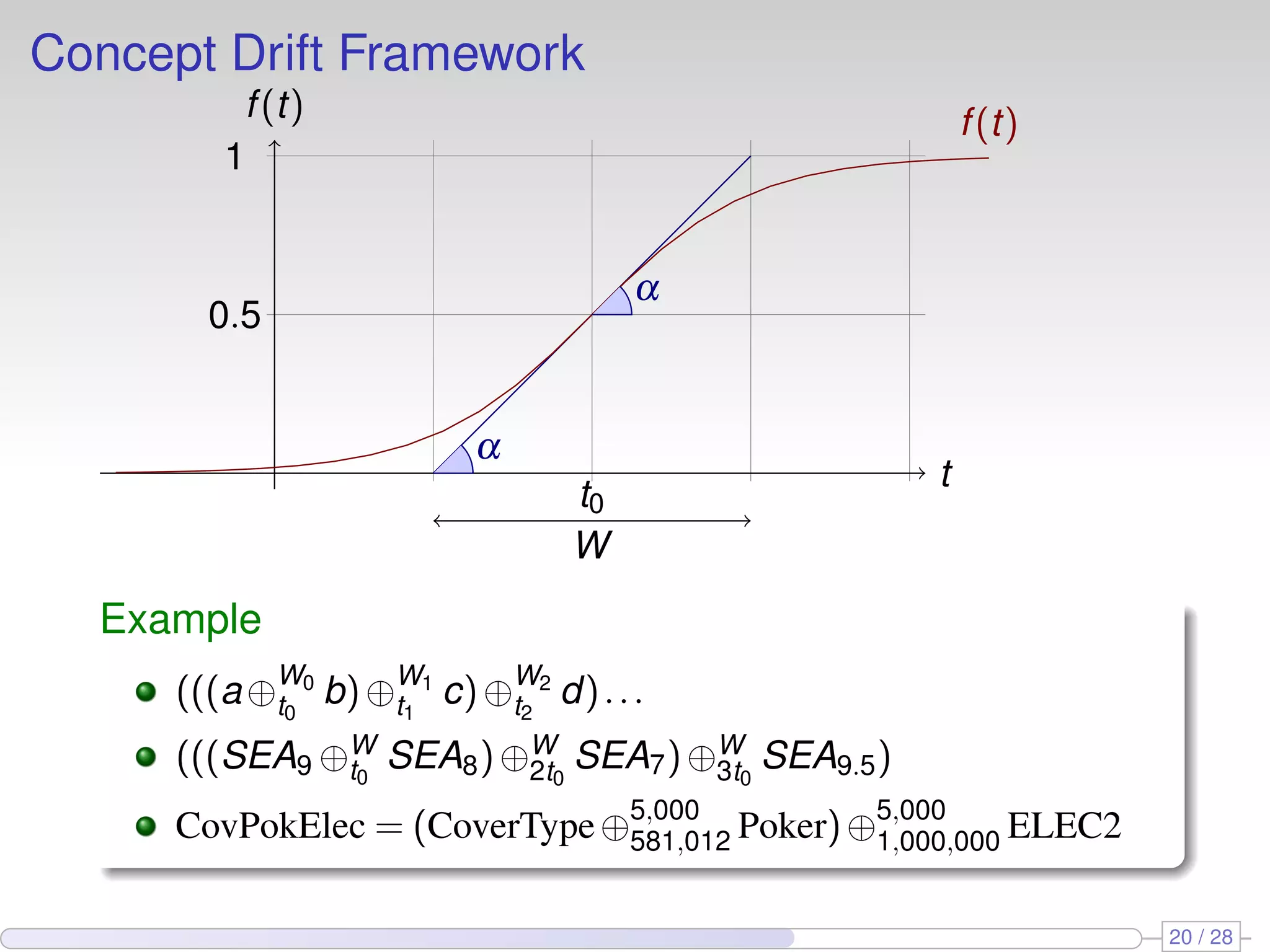
25. Concept Drift Framework
t
f(t) f(t)
α
α
t0
W
0.5
1
Definition
Given two data streams a, b, we define c = a⊕W
t0
b as the data
stream built joining the two data streams a and b
Pr[c(t) = b(t)] = 1/(1+e−4(t−t0)/W ).
Pr[c(t) = a(t)] = 1−Pr[c(t) = b(t)]
20 / 28

26. Concept Drift Framework
t
f(t) f(t)
α
α
t0
W
0.5
1
Example
(((a⊕W0
t0
b)⊕W1
t1
c)⊕W2
t2
d)...
(((SEA9 ⊕W
t0
SEA8)⊕W
2t0
SEA7)⊕W
3t0
SEA9.5)
CovPokElec = (CoverType⊕5,000
581,012 Poker)⊕5,000
1,000,000 ELEC2
20 / 28

27. Empirical evaluation
Accuracy
40
45
50
55
60
65
70
75
80
10.000 120.000 230.000 340.000 450.000 560.000 670.000 780.000 890.000 1.000.0
Instances
Accuracy(%)
htnbp
htnb
htp
ht
Figure: Accuracy on dataset LED with three concept drifts.
21 / 28

28. Empirical evaluation
RunTime
0
5
10
15
20
25
30
35
10.000 120.000 230.000 340.000 450.000 560.000 670.000 780.000 890.000
Instances
Time(sec.)
htnbp
htnb
htp
ht
Figure: Time on dataset LED with three concept drifts.
22 / 28

29. Empirical evaluation
Memory
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
10.000 130.000 250.000 370.000 490.000 610.000 730.000 850.000 970.000
Instances
Memory(Mb)
htnbp
htnb
htp
ht
Figure: Memory on dataset LED with three concept drifts.
23 / 28

30. Empirical evaluation
RAM-Hours
0,00E+00
5,00E-06
1,00E-05
1,50E-05
2,00E-05
2,50E-05
3,00E-05
3,50E-05
4,00E-05
4,50E-05
10.000 130.000 250.000 370.000 490.000 610.000 730.000 850.000 970.000
Instances
RAM-Hours
htnbp
htnb
htp
ht
Figure: RAM-Hours on dataset LED with three concept drifts.
24 / 28

31. Empirical evaluation Cover Type Dataset
Accuracy Time Mem RAM-Hours
Perceptron 81.68 12.21 0.05 1.00
Na¨ıve Bayes 60.52 22.81 0.08 2.99
Hoeffding Tree 68.3 13.43 2.59 56.98
Trees
Na¨ıve Bayes HT 81.06 24.73 2.59 104.92
Perceptron HT 83.59 16.53 3.46 93.68
NB Perceptron HT 85.77 22.16 3.46 125.59
Bagging
Na¨ıve Bayes HT 85.73 165.75 0.8 217.20
Perceptron HT 86.33 50.06 1.66 136.12
NB Perceptron HT 87.88 115.58 1.25 236.65
25 / 28

32. Empirical evaluation Electricity Dataset
Accuracy Time Mem RAM-Hours
Perceptron 79.07 0.53 0.01 1.00
Na¨ıve Bayes 73.36 0.55 0.01 1.04
Hoeffding Tree 75.35 0.86 0.12 19.47
Trees
Na¨ıve Bayes HT 80.69 0.96 0.12 21.74
Perceptron HT 84.24 0.93 0.21 36.85
NB Perceptron HT 84.34 1.07 0.21 42.40
Bagging
Na¨ıve Bayes HT 84.36 3.17 0.13 77.75
Perceptron HT 85.22 2.59 0.44 215.02
NB Perceptron HT 86.44 3.55 0.3 200.94
26 / 28

33. Summary
http://moa.cs.waikato.ac.nz/
Summary
Sensor Networks
use Perceptron
Handheld Computers
use Hoeffding Naive Bayes Perceptron Tree
Servers
use Bagging Hoeffding Naive Bayes Perceptron Tree
27 / 28

34. Summary
http://moa.cs.waikato.ac.nz/
Conclusions
RAM-Hours as a new measure of time and memory
Hoeffding Perceptron Tree
Hoeffding Naive Bayes Perceptron Tree
Future Work
Adaptive learning rate for the Perceptron.
28 / 28