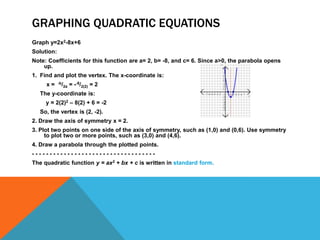
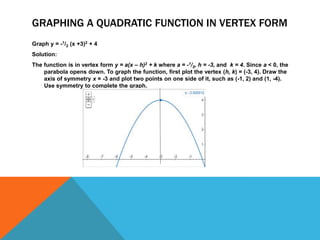
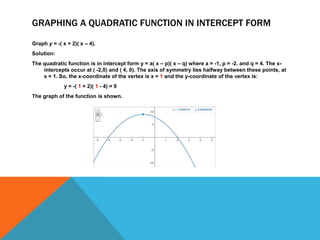
The document provides instructions for graphing and solving various types of quadratic equations. It defines standard form, vertex form, and intercept form of quadratics. It explains how to graph quadratics by finding the vertex and intercepts. Methods covered include factoring, taking square roots, completing the square, and using the quadratic formula. Examples are included to demonstrate each process.

2. GRAPHING QUADRATIC EQUATIONS
Graph y=2x2-8x+6
Solution:
Note: Coefficients for this function are a= 2, b= -8, and c= 6. Since a>0, the parabola opens
up.
1. Find and plot the vertex. The x-coordinate is:
x= -b/ = --8/2(2) = 2
2a
The y-coordinate is:
y = 2(2)2 – 8(2) + 6 = -2
So, the vertex is (2, -2).
2. Draw the axis of symmetry x = 2.
3. Plot two points on one side of the axis of symmetry, such as (1,0) and (0,6). Use symmetry
to plot two or more points, such as (3,0) and (4,6).
4. Draw a parabola through the plotted points.
-----------------------------------
The quadratic function y = ax2 + bx + c is written in standard form.

3. GRAPHING A QUADRATIC FUNCTION IN VERTEX FORM
Graph y = -1/2 (x +3)2 + 4
Solution:
The function is in vertex form y = a(x – h)2 + k where a = -1/2, h = -3, and k = 4. Since a < 0, the
parabola opens down. To graph the function, first plot the vertex (h, k) = (-3, 4). Draw the
axis of symmetry x = -3 and plot two points on one side of it, such as (-1, 2) and (1, -4).
Use symmetry to complete the graph.

4. GRAPHING A QUADRATIC FUNCTION IN INTERCEPT FORM
Graph y = -( x + 2)( x – 4).
Solution:
The quadratic function is in intercept form y = a( x – p)( x – q) where a = -1, p = -2. and q = 4. The x-
intercepts occur at ( -2,0) and ( 4, 0). The axis of symmetry lies halfway between these points, at
x = 1. So, the x-coordinate of the vertex is x = 1 and the y-coordinate of the vertex is:
y = -( 1 + 2)( 1 - 4) = 9
The graph of the function is shown.

5. WRITING QUADRATIC FUNCTIONS IN STANDARD FORM
Write the quadratic function in standard form.
a. Y = -( x+4)( x – 9) b. y = 3( x – 1)2 +8
Solution:
a. y = -( x +4)( x – 9) Write original function.
= -( x2 – 9x +4x – 36) Multiply by using FOIL.
= -( x2 – 5x – 36) Combine like terms.
= -x2 + 5x +36 Use distributive property.
b. y = 3( x – 1)2 +8 Write original function.
= 3( x – 1)( x – 1) + 8 Rewrite ( x - 1)2.
= 3(x2 - x – x + 1) + 8 Multiply using FOIL.
= 3( x2 – 2x + 1) +8 Combine like terms.
= 3x2 – 6x + 3 + 8 Use distributive property.
= 3x2 – 6x + 11 Combine like terms.

6. SOLVING QUADRATIC EQUATIONS WITH FACTORING
( X + 3)( X + 5) can be written as x2 + 8x + 15. The expressions x + 3 and x + 5 are
binominals because they have two terms. The expression x2 + 8x + 15 is a
trinomial because it has three terms. You can use factoring to write a trinomial as
a product of binominals. To factor x2 + bx + c, find integers m and n such that:
x2 + bx + c = ( x + m)( x + n)
= x2 + ( m + n)x + mn
So, the sum of m and n must equal b and the product of m and n must equal c.
Factoring Shortcuts:
Difference of Two Squares: a2 – b2 = (a + b)(a – b), Example: x2 – 9 = ( x + 3)( x –
3)
Perfect Square Trinomial: a2 + 2ab + b2 = ( a + b)2, Example: x2 +12x + 36 = ( x
+6)2
a2 - 2ab + b2 = ( a - b)2, Example: x2 – 8x + 16 = ( x – 4)2

7. FACTORING A TRINOMIAL OF THE FORM X2 + BX + C
Factor x2 - 12x – 28
Solution:
You want x2 – 12x – 28 = ( x + m)(x + n) where mn = -28 and m + n = -12.
Factors of -28 -1, 28 1, -28 -2, 14 2, -14 -4, 7 4, -7
(m, n)
Sum of factors 27 -27 12 -12 3 -3
( m + n)
The table shows that m = 2 and n = -14. So, x2 – 12x – 28 = ( x + 2)( x – 14).

8. FACTORING A TRINOMIAL OF THE FORM AX2 + BX + C
Factor 3x2 – 17x + 10.
Solution:
You want 3x2 – 17x + 10 = ( kx + m)( lx + n ) where k and l are factors of 3 and m and n
are (negative) factors of 10. Check possible factorization by multiplying.
( 3x – 10)( x – 1) = 3x2 – 11x + 10 ( 3x – 1)( x – 10) = 3x2 – 31x + 10
( 3x – 5)( x – 2) = 3x2 – 11x + 10 ( 3x – 2)( x – 5) = 3x2 – 17x + 10 
Correct
The correct factorization is 3x2 – 17x + 10 = ( 3x – 2)( x – 5).

9. SOLVING QUADRATIC EQUATIONS BY FINDING SQUARE ROOTS
A number r is a square root of a number s if r2 = . A positive number s has two square
roots denoted by √s and - √s. The symbol √ is a radical sign, the number s beneath
the radical sign is the radicand, and the expression √s is a radical. For
example, since 32 = 9 and ( -3)2 = 9, the two square roots of 9 are √9 = 3 and - √9 = -
3. You can use a calculator to approximate √s when s is not a perfect square. For
instance, √2 ≈ 1,414.
Example: Using Properties of Square Roots
Simplify the expression:
a. √24 = √4 * √6 = 2 √6 b. √6 * √15 = √90 = √9 * √10 = 3 √16
c. √7/16 = √7/√16 = √7/4 d. √7/2 = √7/√2 * √2/√2 = √14/2
In part (d) of this example, the square root in the denominator of 7/2 was eliminated by
multiplying both the numerator and denominator by √2. This process is called
rationalizing the denominator. You can use square roots to solve some types of
quadratic equations.

10. SOLVING A QUADRATIC EQUATION (√)
Solve 2x2 + 1 = 17
Solution:
Begin by writing the equation in the form x2 = s.
2x2 + 1 = 17 Write original equation.
2x2 = 16 Subtract 1 from each side.
x2 = 8 Divide each side by 2.
x = +/- √8 Take square roots of each side.
x = +/- 2 √2 Simplify.
The solutions are 2√2 and -2√2.

11. SOLVING A QUADRATIC EQUATION (√)
Solve 1/3( x + 5)2 = 7
Solution:
1/ x + 5)2 = 7
3( Write original equation.
( x + 5)2 = 21 Multiply each side by 3
x + 5 = +/- √21 Take square roots of each side.
x = -5 +/- √21 Subtract 5 from each side.
The solutions are -5 + √21 and -5 - √21.

12. COMPLETING THE SQUARE
Completing the square is a process that allows you to write an expression of the form
x2 + bx as the square of a binomial. This process can be illustrated by using an
area model too.
Example: Completing The Square
Find the value of c that makes x2 – 7x + c, note that b = -7, therefore:
c = (b/2)2 = (-7/2)2 = 49/4
Use this value of c to write x2 – 7x + c as a perfect square trinomial, and then as the
square of a binomial.
x2 – 7x + c = x2 – 7x + 49/4 Perfect square trinomial.
= ( x – 7/2)2 Square of a binomial: ( x + b/2)2

13. SOLVING A QUADRATIC EQUATION IF THE COEFFICIENT OF X2 IS NOT 1
Solve 3x2 – 6x + 12 = 0 by completing the square.
Solution:
3x2 – 6x + 12 = 0 Write original equation.
x2 – 2x + 4 = 0 Divide each side by the coefficient of x2.
x2 – 2x = -4 Write the left side in the form of x2 + bx.
x2 – 2x + (-1)2 = -4 + 1 Add (-2/2)2 = (-1)2 = 1 to each side.
( x – 1)2 = -3 Write the left side as a binomial squared.
x – 1 = +/- √-3 Take square roots of each side.
x = 1 +/- √-3 Solve for x
x = 1 +/- i√3 Write in terms of imaginary unit i.
The solutions are 1 + i√3 and 1 - i√3.
Because these solutions are imaginary, you cannot check them graphically. However, you can check
the solutions algebraically by substituting them back into the original equation.

14. SOLVING A QUADRATIC EQUATION IF THE COEFFICIENT OF X2 IS 1
Solve x2 + 10x – 3 = 0 by completing the square.
Solution:
x2 + 10x – 3 = 0 Write original equation.
x2 + 10x = 3 Write the left side in the form x2 + bx.
x2 + 10x +52 = 3 + 25 Add (10/2)2 = 52 = 25 to each side.
( x + 5)2 = 28 Write the left side as a binomial squared.
x + 5 = +/- √28 Take square roots of each side.
x = -5 +/- √28 Solve for x.
x = -5 +/- 2 √7 Simplify.
The solutions are -5 + 2 √7 and -5 - 2 √7.

15. QUADRATIC FORMULA AND DISCRIMINANT
The Quadratic Formula:
Let a, b, and c be real numbers such that a ≠ 0. The solutions of the quadratic
equation ax2 + bx + c = 0 are:
x = -b +/- √b2 – 4ac/ 2a
Remember that before you apply the quadratic formula to a quadratic equation, you
must write the equation in standard form, ax2 + bx + c = 0.

16. SOLVING A QUADRATIC EQUATION WITH TWO REAL SOLUTIONS
Solve 2x2 + x = 5
Solution:
2x2 + x = 5 Write original equation.
2x2 + x – 5 = 0 Write in standard form.
2 – 4ac
x = -b +/- √b / 2a Quadratic formula
x = -1 +/- √12 – 4(2)(-5)/ 2(2) a = 2, b = 1, c = -5
x = -1 +/- √41/4 Simplify.
The solutions are x = -1 +/- √41/4 ≈ 1.35, and x = -1 +/- √41/4 ≈ 1.85