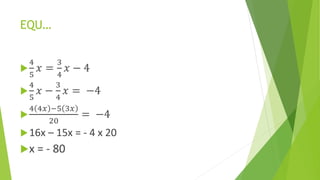This document provides an introduction to linear equations, including definitions, examples of solving different types of linear equations (e.g. one-step, two-step, fractional), and exponential equations. It defines an equation as a statement that two expressions are equal. Examples are provided to demonstrate solving single-variable linear equations algebraically by adding or subtracting the same quantity to both sides of the equation to isolate the variable. The document also covers solving equations with fractions, as well as exponential equations by equating exponents or bases as appropriate. Practice problems with solutions are provided.

1. LINEAR EQUATIONS: AN
INTRODUCTION (G9)
DEFINITION AND EXAMPLES

2. DEFINITION
AN EQUATION: is a statement that says that 2
expressions are equal.
For example two R5 coins is equivalent to R10
we can write it down as 2(R5) = R10

3. What you do on the left should be done on
the right to keep the equation balanced
2(R5) = R10
2(R5) – R1 = R10 –R1
2(R5) + R20 = R10 + R20
X + 3 = 5

4. X + 3 = 5
x+3-3 = 5 -3
x = 2
(2) + 3 = 5

5. X + 6 = 15
x +6 -6 = 15 -6
x = 9
2x + 3 = 13

6. 2x + 3 = 13
2x +3 -3 = 13 -3
2x = 10
2x/2 = 10/2
x = 5
2(x +4) =20

7. 2(x +4) = 20
2x + 8 =20
2x +8 – 8 = 20 -8
2x = 12
2x/2 = 12/2
x = 6
2(x+4) = 20
2(x+4)/2 = 20/2
X + 4 = 10
X = 10-4
X= 6

8. 2x -3 = 4x -6
2x – 4x = 3-6
-2x = -3
-2x/-2 = -3/-2
x= 3/2
2x +10 = 3x - 4

9. 2x +10 = 3x – 4
2x -3x = -4-10
-x = -14
-x/-1 =-14/-1
x = 14
X squared -9 = 0
(x +3)(x -3) = 0
(x+3) = 0 or (x-3) = 0
X= -3 or x = 3

10. DIFFERENCE OF TWO SQUARES (DOTS)
X2 – 9 = 0
(x +3)(x-3) =0
x+3 = 0 or x – 3 = 0
x = 3 or x = -3

11. X2 – 25 = 0
(x+5)(x-5) = 0
x+5 = 0 or x- 5 = 0
x = -5 or x = 5
2x2 – 2 = 0
2(x2 -1) = 0 (divide both sides by 2)
x2 -1 = 0
(x+1)(x-1) =0
x+1 = 0 or x-1 =0
x= -1 or x = 1

12. 25(x2 – 4) = 0 (divide both sides by 25)
x2 – 4 = 0
(x-2)(x+2) = 0
x-2 = 0 or x+2 =0
x = 2 or x = -2
X2 – 7 = 9
x2 – 7-9 =0
x2-16 = 0
(x-4)(x+4) = 0
x- 4 = 0 or x+4 =o
x= 4 or x = -4

13. X3 – x = 0
x(x2-1) =0
x(x+1)(x-1) = 0
x= 0 or x+1 = 0 or x-1 =0
x=0 or x= -1 or x= 1
the power of x tells us how many values
of x will make up our solution.

14. EXERCISE
 SOLVE FOR X IN THE FOLLOWING EQUATIONS
 1. x + 1 = 6 x = 5
 2. x – 6 = 1 x = 7
 3. 2x + 4 = 10 x = 3
 4. 3x – 6 = 14 -2x x = 4
 5. X2 – 81 = 0 x = 9 or x = -9
 6. X2 – 4 = 0 x = 2 or x = -2
 7. 2x2 – 32 = 0 x = 4 or x = -4
 8. 25x2 – 1 = 0 x = 1/5 or x = -1/5

15. TRINOMIAL EQUATIONS
 1. (x-2)(x-3) = 0 x2 -5x + 6 = 0
 x-2 =0 or x-3 = 0 (2x2)-5(2) +6 = 4-10+6
 X = 2 or x = 3 = -6+6 =0
 2. (x-4)(x+5) = 0 x2 + x -20 = 0
 X- 4 = 0 or x + 5 = 0 (x -4 )(x+5 ) = 0
 X = 4 or x= - 5

16. 3. (x+2)(x+6) = 0 x2 + 8x + 12 = 0
x+2 = 0 or x+6 = 0
x= -2 or x = -6

17. (x-3)(x+4) = -6
x2 + x – 12 = -6
X2 + x -12 + 6 = 0
X2 +x – 6 = 0
(x +3)(x-2) = 0
X2 – 25 =0

18. EXERCISE
Solve for x in the following
1. x + 4 = 10 x = 6
2. x -15 = 3 x = 18
3. 2x + 5 = 3x- 10 x = 15
4. X2 = 25 x= 5 or x = -5
5. X2 +10 = 11 x = 1 or x = -1
6. 3x2 + 6 = 18 x = -2 or x = 2
7. (x+3)(x+6) = 0 x = -3 or x = -6
8. X2 + 4x – 12 = 0 x = -6 or x = 2
9. X2 + 5x = -6 x = -2 or x = -3

19. SOLUTIONS
1. x + 4 = 10
x = 10 – 4
x = 6
2. x -15 = 3
x = 3 + 15
x = 18
3. 2x + 5 = 3x- 10
5+10 = 3x -2x
15 = x
x = 15

20. X2 + 4x – 12 = 0
(x +6)(x-2) = 0
x = -6 or x = 2
X2 + 5x = -6
X2 + 5x +6 = 0
(x+2)(x+3) = 0
x = -2 or x = -3

21. EQUATIONS WITH FRACTIONS

1
2
𝑥 = 10
X = 10 x 2
X= 20

22. EQU…

3
5
𝑥 = 15
3x = 15 x 5
3x = 75
x = 75/3
x= 25

23. EQU…

4
5
𝑥 =
3
4
𝑥 − 4

4
5
𝑥 −
3
4
𝑥 = −4

4 4𝑥 −5 3𝑥
20
= −4
16x – 15x = - 4 x 20
x = - 80

24. CLASSWORK: solve for x
1.
1
3
𝑥 = 9 x = 27
2.
2
5
𝑥 = 10 x = 25
3.
7
8
𝑥 = 1 x = 8/7
4.
1
2
𝑥 +
1
3
𝑥 = 5 x = 6
5.
3
4
𝑥 − 4 = 0 x = 16/3
6.
3
7
𝑥 + 2 =
1
4
𝑥 − 3 x = -28
7. X2-
1
4
= 0 x = ½ or x= -1/2

25. EXPONENTIAL EQUATIONS
 EXAMPLES
1. 2X = 27
X = 7
2. 5X = 56
x= 6
3. X4 = 34
x = 3
2 is the base
7 is the exponent
When the basis are the same, then equate the
powers. If powers are the same, then equate
the bases.

26. Expo…
1. 2x3 = 54
x3 = 27
x3 = 33
x = 3
2. (3x)3 = 3
33x = 31
3x = 1
x = 1/3
Write 27 as a power of
3
Don’t multiply a base and a coefficient.
NOTES

27. Expo..
1. 2x – 25 = -17
2x = -17 +25
2x = 8
2x = 23
x= 3

28. CLASSWORK
1. 2x = 128 x = 7
2. 5x = 53 x = 3
3. 7x = 343 x = 3
4. 2x + 9 = 25 x = 4
5. 27(3x) = 3 x = -2
6. 7x – 9 = -8 x = 0
7. 8x-8 = 8 x = 9
8. 4x + 7 = 23 x = 2