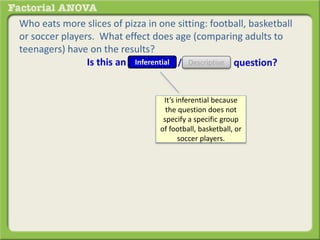
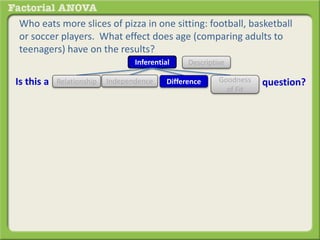
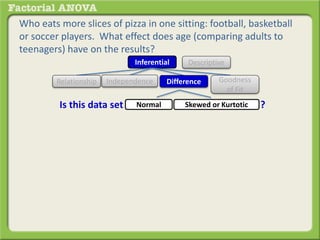
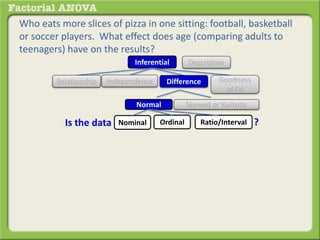
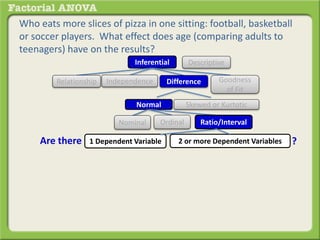
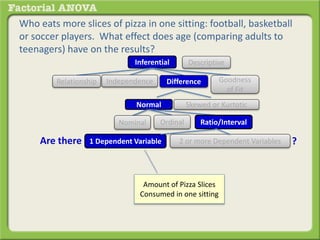
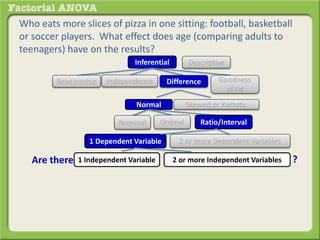
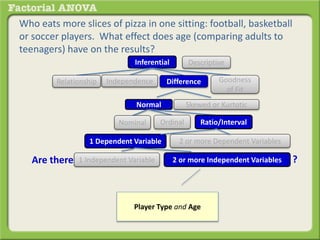
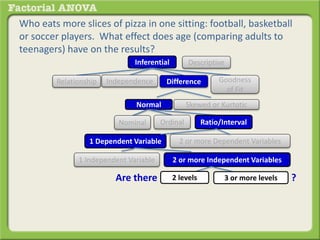
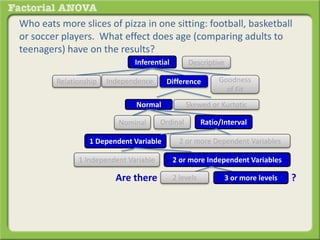
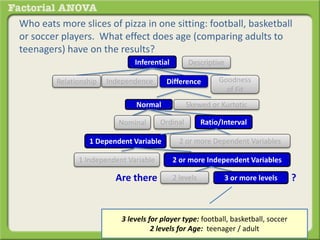
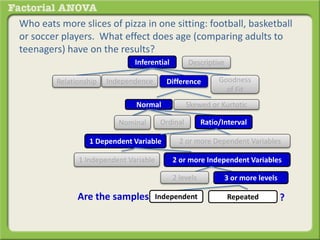
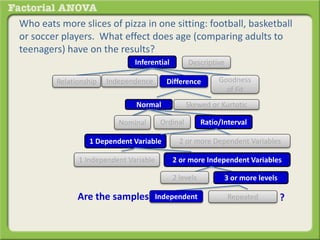
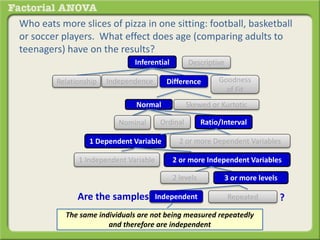
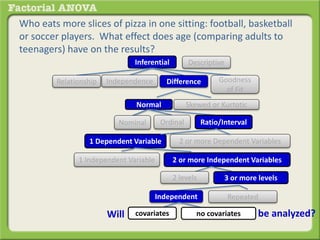
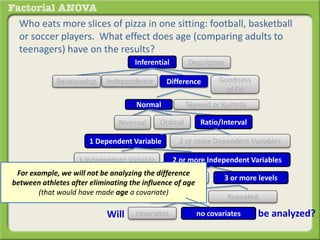
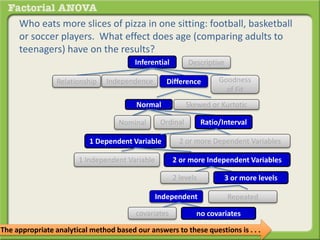
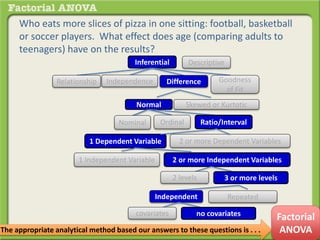
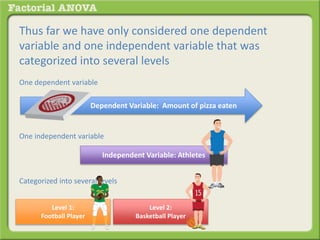
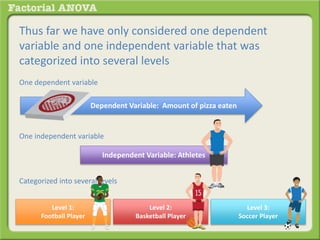
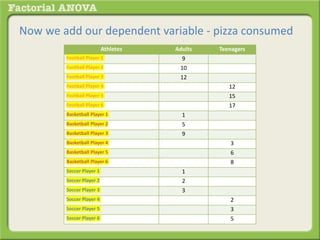
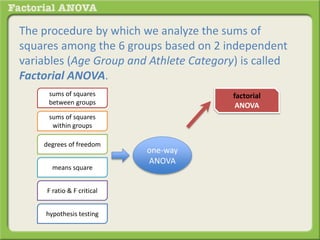
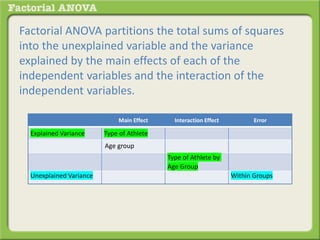
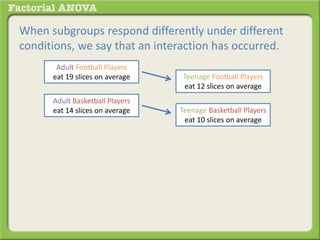
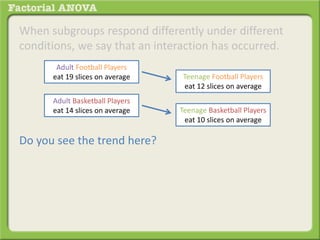
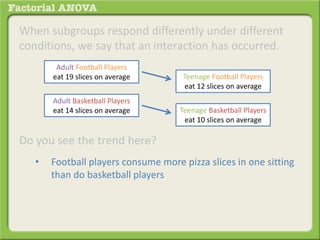
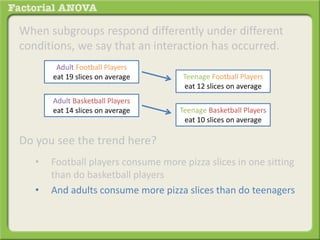
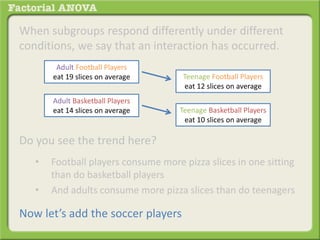
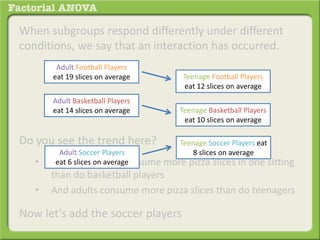
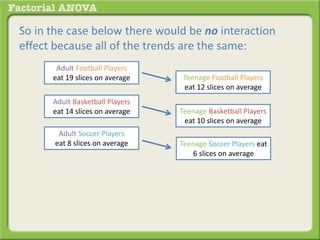
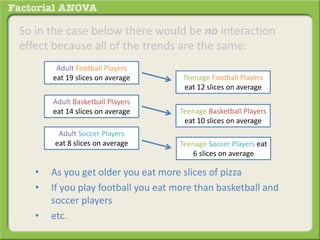
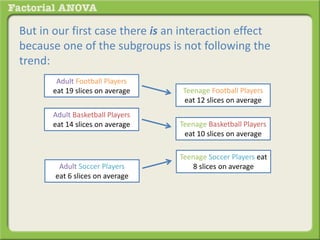
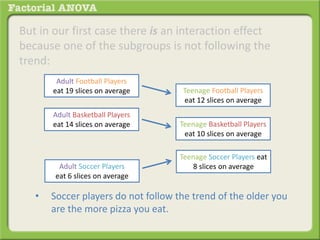
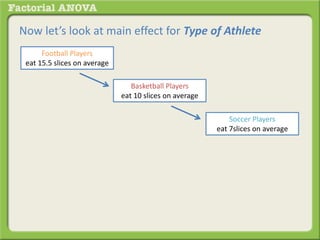
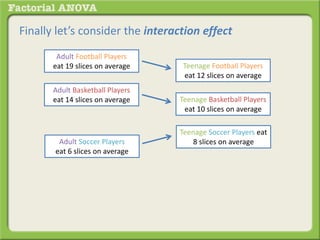
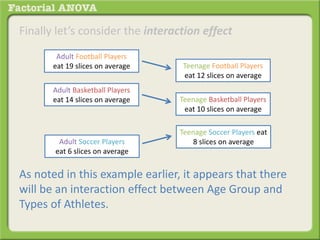
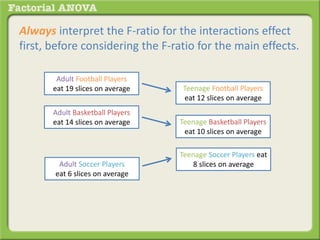
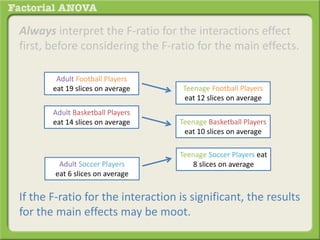
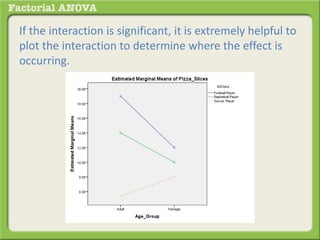
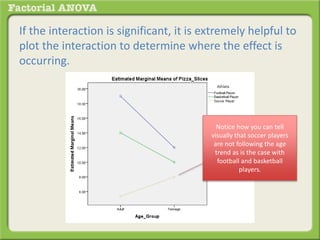
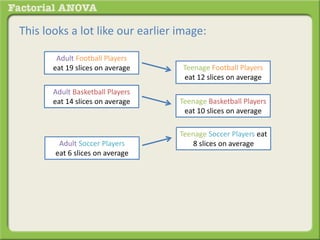
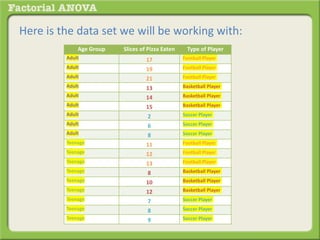
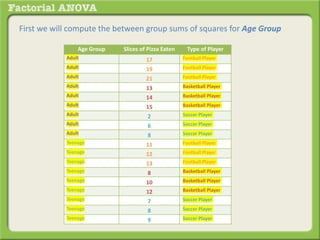
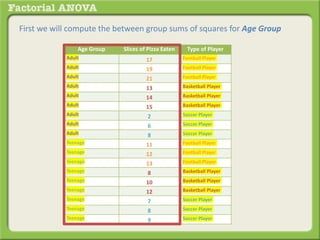
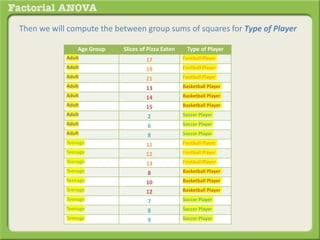
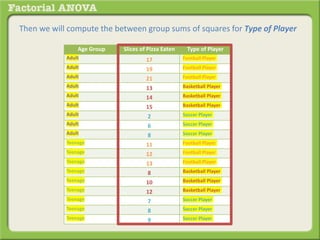
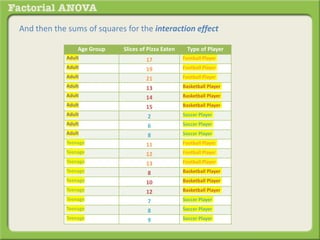
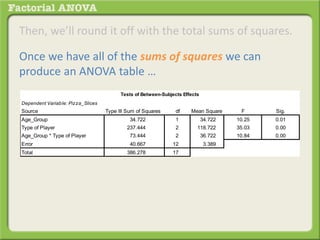
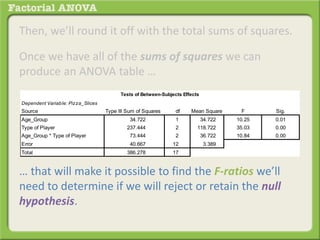
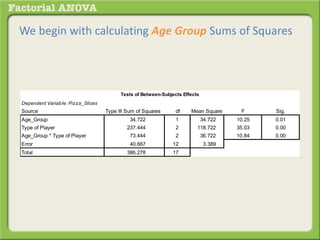
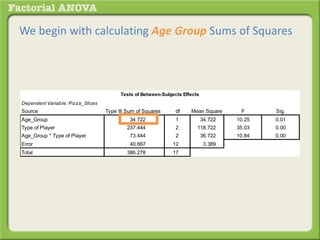
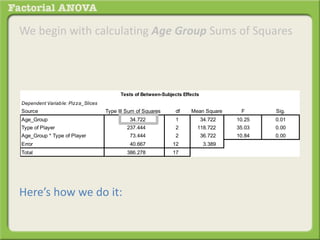
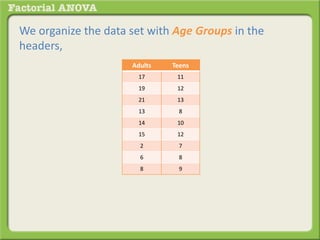
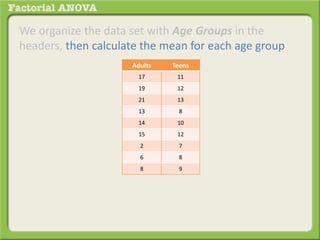
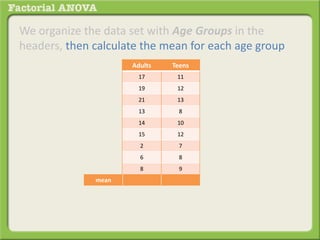
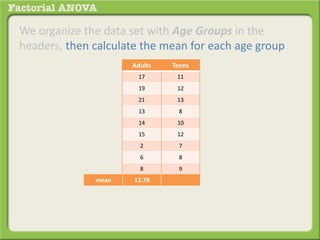
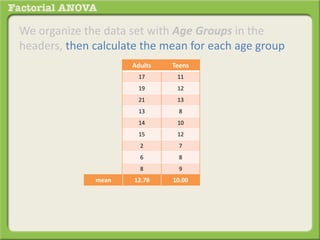
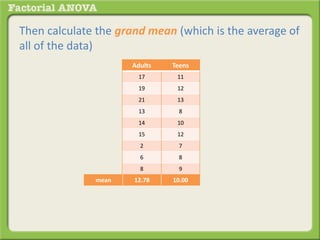
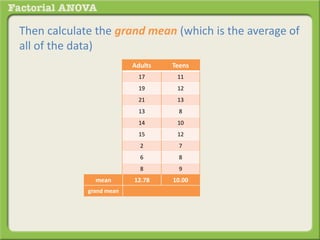
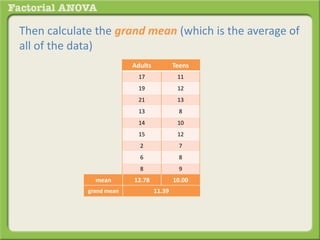
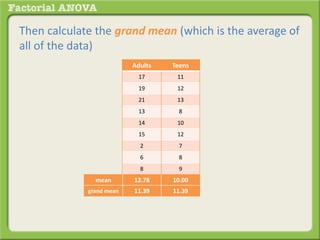
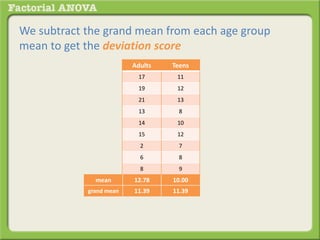
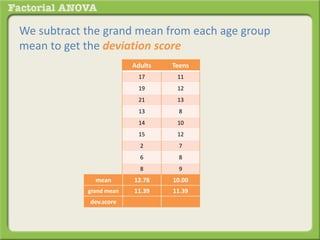
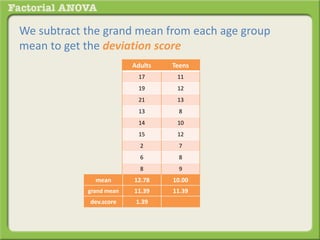
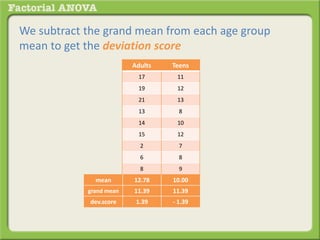
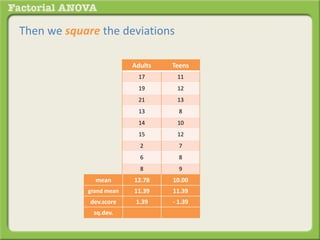
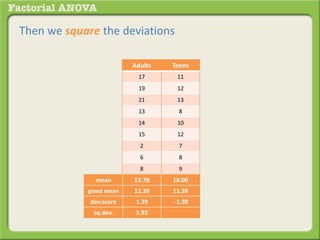
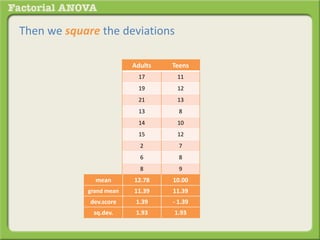
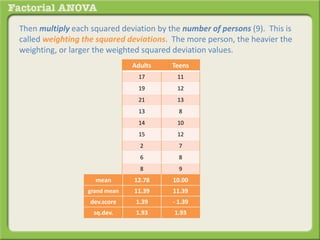
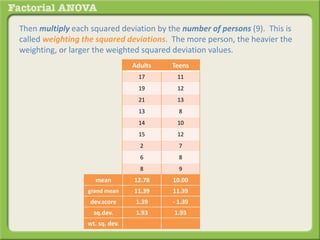
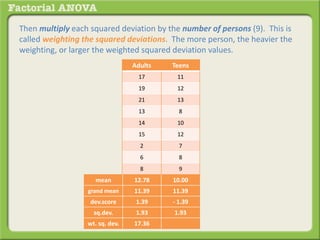
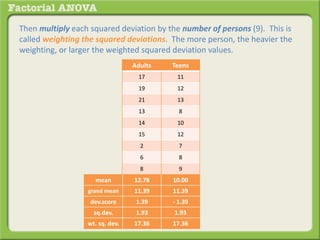
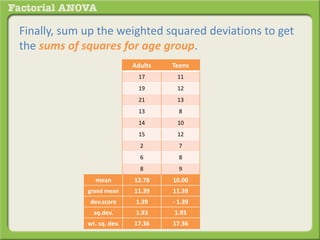
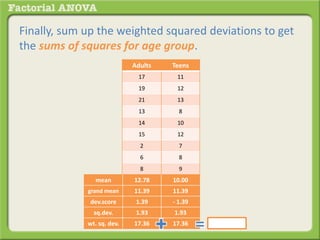
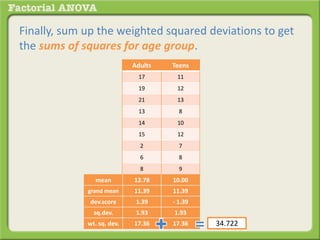
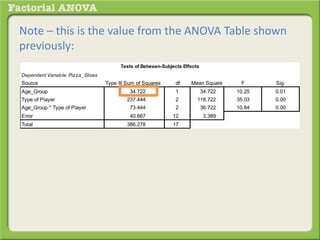
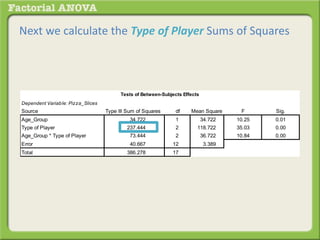
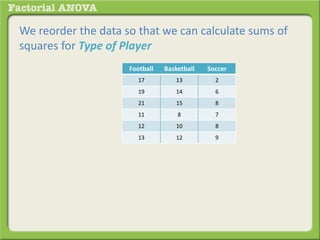
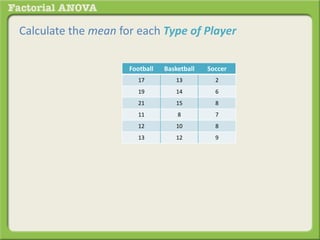
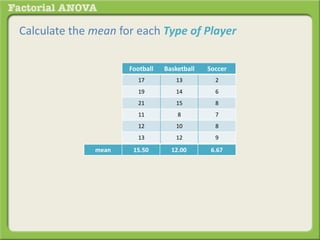
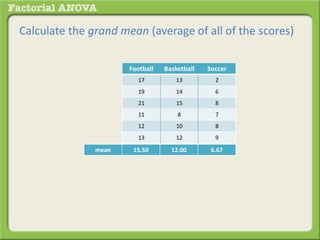
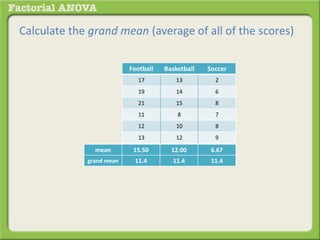
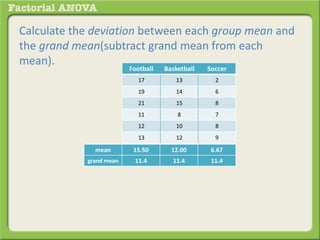
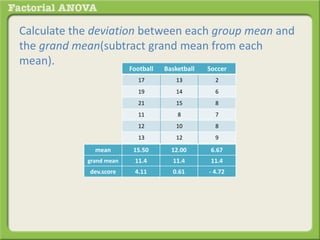
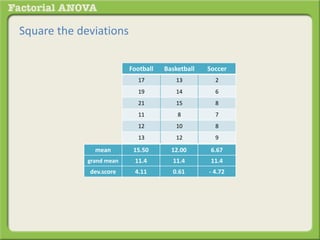
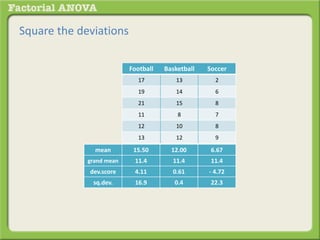
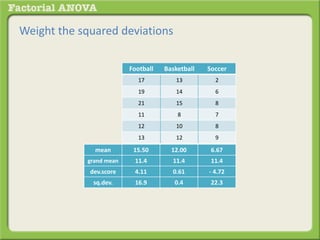
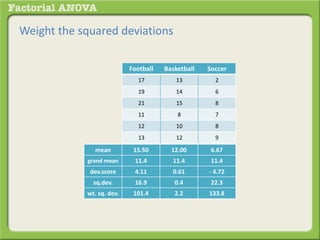
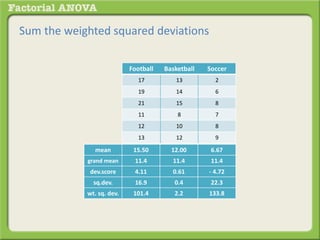
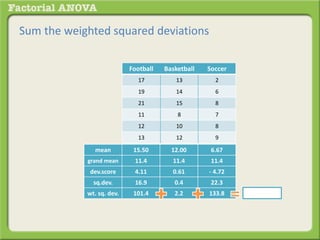
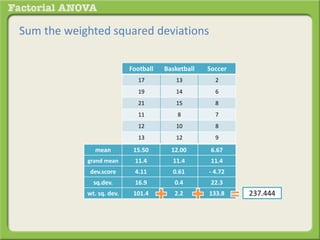
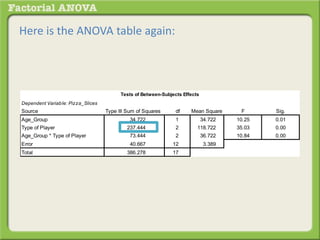
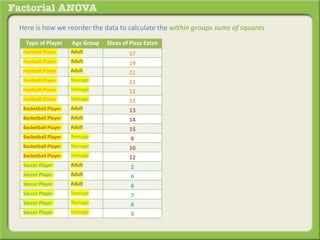
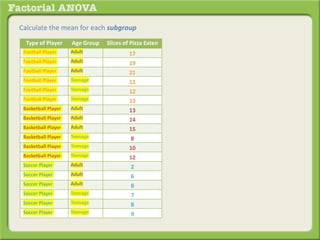
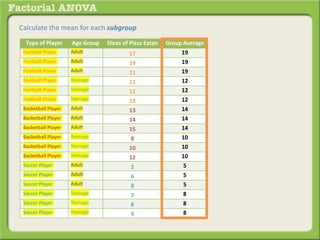
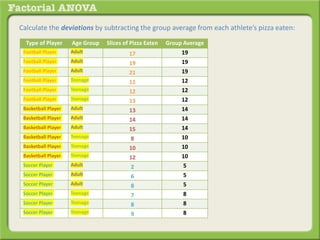
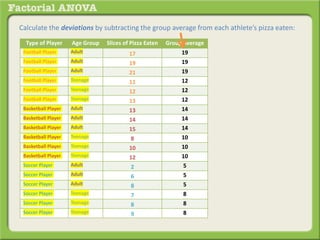
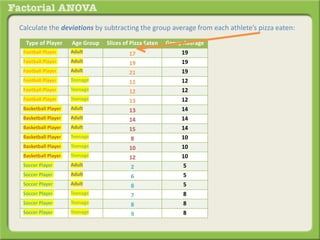
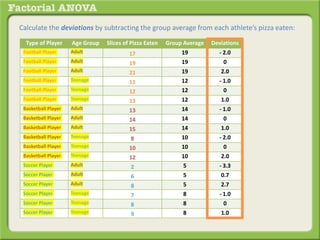
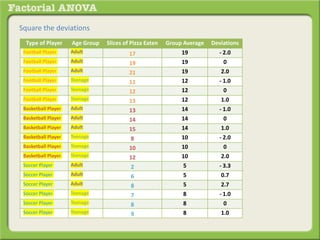
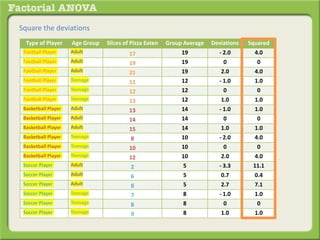
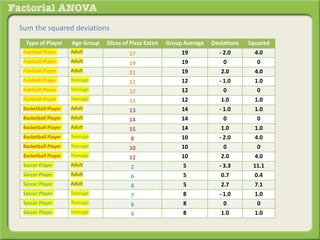
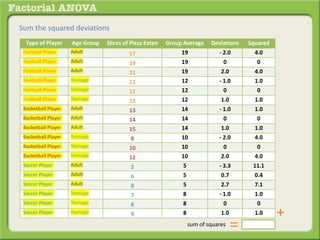
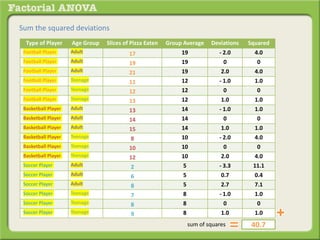
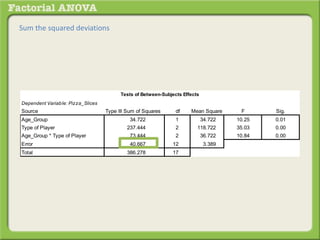
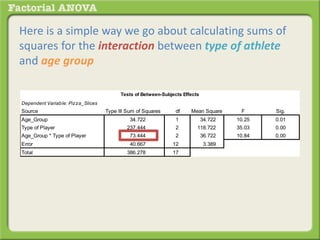
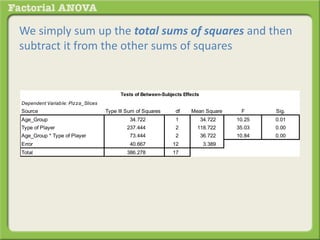
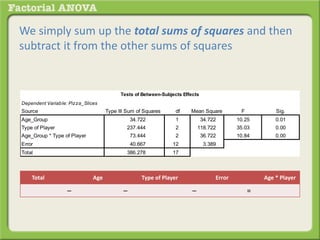
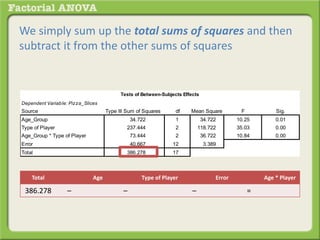
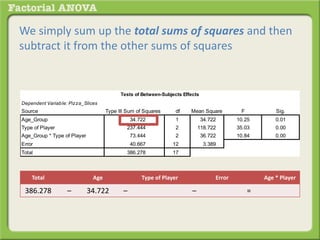
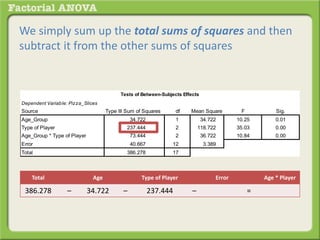
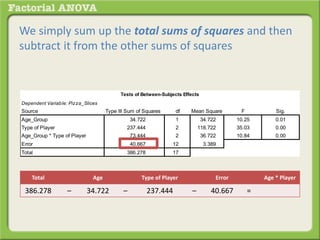
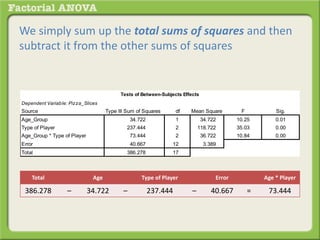
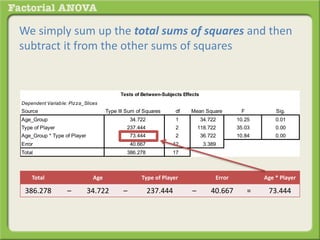
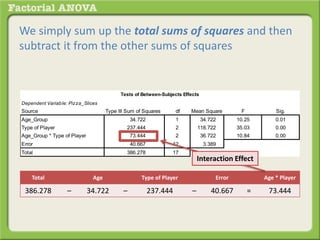
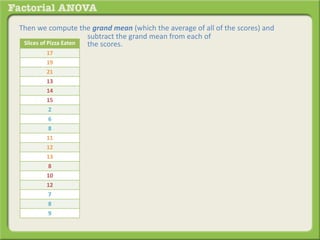
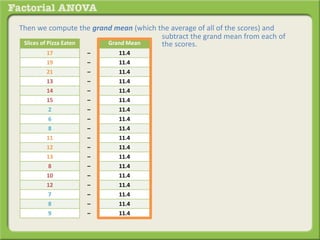
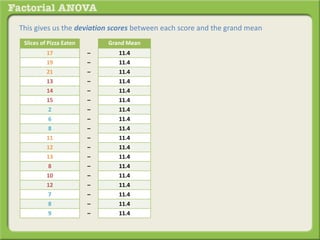
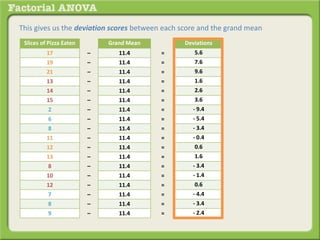
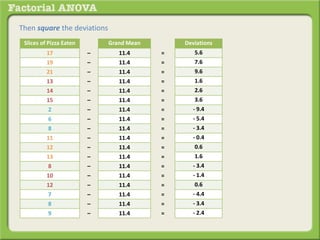
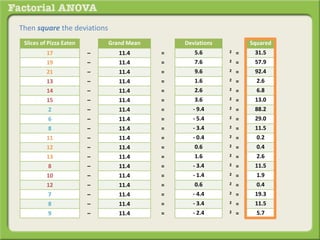
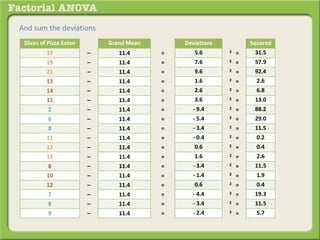
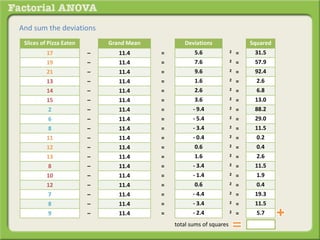
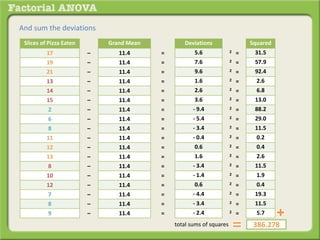
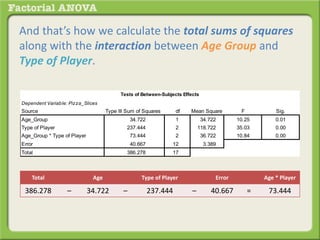
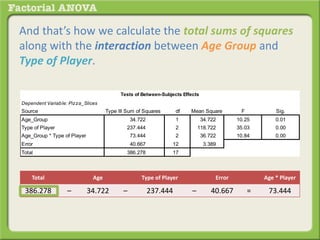
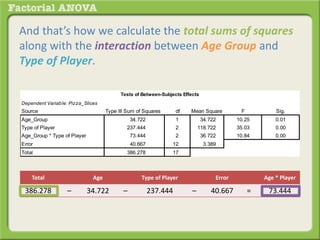
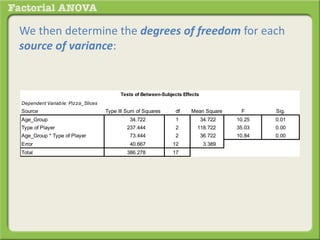
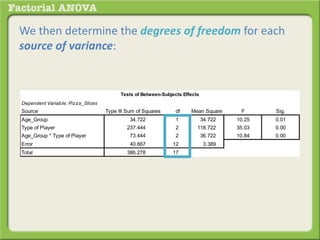
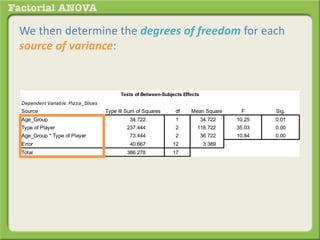
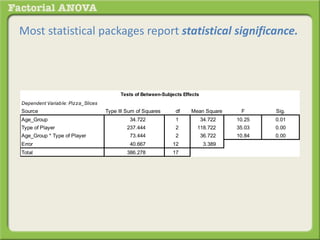
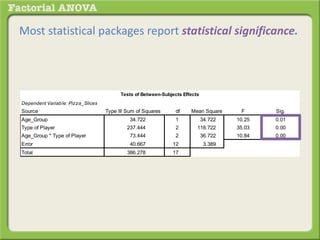
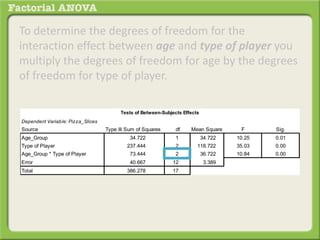
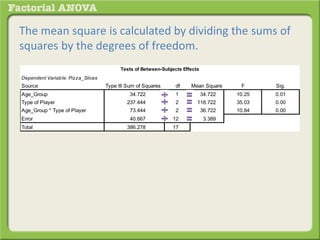
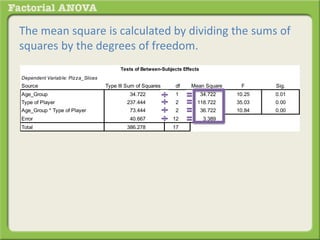
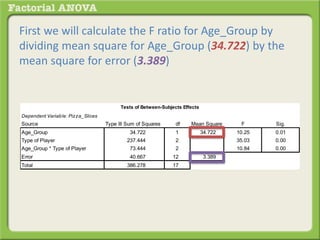
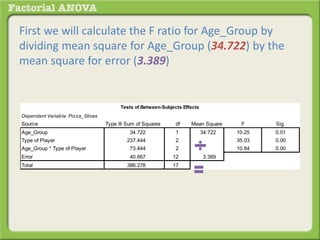
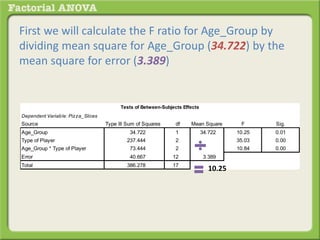
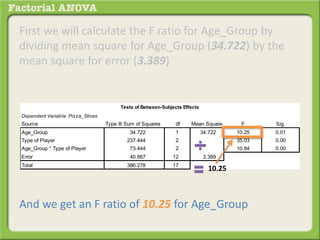
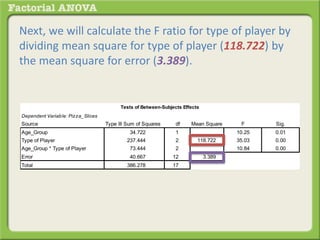
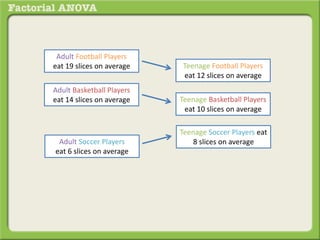
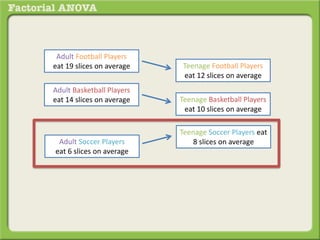
The document discusses conducting a factorial analysis of variance (ANOVA) to analyze the effects of two independent variables, athlete type (football, basketball, soccer players) and age (adults vs teenagers), on the dependent variable of number of slices of pizza consumed. It outlines setting up a 2x3 factorial design to compare the six groups that results from the two independent variables, each with multiple levels, and determining that a factorial ANOVA is the appropriate statistical analysis for this research question and study design.