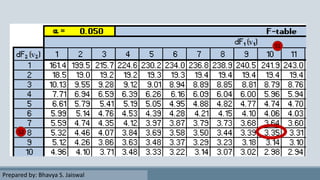
The document discusses the F-test, which is used to determine if the variances of two populations are significantly different. It explains that the F-test involves calculating the F-value, which is the ratio of the larger sample variance to the smaller sample variance. This F-value is then compared to a critical value from the F-distribution table based on the degrees of freedom. If the F-value is less than the critical value, there is no significant difference between the population variances. The document provides an example calculation to demonstrate how to perform an F-test on two samples and determine if their variances are significantly different or not.

1. F-Test
R.A. FISHER
Bhavya S. Jaiswal
Btech civil, Mtech Transportation Engineering

2. Content of the presentation
Objective
Relation with traffic engineering
How it is conducted?
Numerical
Prepared by: Bhavya S. Jaiswal

3. Objective of F-test
To find out whether the two independent estimate of population
variance differ significantly.
Prepared by: Bhavya S. Jaiswal

4. How the F-test is related to the traffic
engineering ?
Suppose, if we have a study area which is
divided in two zones and we are taking the
observation from both the zones…
at this time we have to check whether
the data which is obtained by different zones
have a significance difference or not! In such
case, the F-test is used.
1
2
Prepared by: Bhavya S. Jaiswal

5. To find this significance, we have to apply the following formula to find out the
F-Value…
F=
𝑆12
𝑆22 where, always 𝑆12>𝑆22
So, in simple words ,
F=
𝐿𝑎𝑟𝑔𝑒𝑟 𝑒𝑠𝑡𝑖𝑚𝑎𝑡𝑒 𝑜𝑓 𝑣𝑎𝑟𝑖𝑎𝑛𝑐𝑒
𝑠𝑚𝑎𝑙𝑙𝑒𝑟 𝑒𝑠𝑡𝑖𝑚𝑎𝑡𝑒 𝑜𝑓 𝑣𝑎𝑟𝑖𝑎𝑛𝑐𝑒
𝑺𝟐
=
(𝑿 − 𝑿)
𝟐
𝑵 − 𝟏
X= variance
𝑿= mean
N= number of variance
(N-1)= Degree of
freedom
Prepared by: Bhavya S. Jaiswal

6. After obtaining the F value , it is compared with the tabulated F-value according to
degree of freedom at 1% or 5%.
1. If the tabulated F-Value > calculated F-value , than there is no significant
difference between two variables.
2. If the tabulated F-Value < calculated F-value , than there is a significant
difference between two variables.
As we can see, F test is the ratio of two variance hence, F test is also called as
“Variance Ratio Test”.
Prepared by: Bhavya S. Jaiswal

7. Numerical
Q. Two random samples were drawn from two normal of populations and the
values are as shown below.
A = 16,17,25,26,32,34,38,40,42
B = 14,16,24,28,32,35,37,42,43,45,47.
than test whether these two population have a same variance at 5% level of
significance.
Prepared by: Bhavya S. Jaiswal

8. Solution
A = 16,17,25,26,32,34,38,40,42; n=9
B = 14,16,24,28,32,35,37,42,43,45,47; n=11
A (𝑋 − 𝑿) (𝑋 − 𝑿)𝟐 B (𝑋 − 𝑿) (𝑋 − 𝑿)𝟐
16 -14 196 14 -19 361
17 -13 169 16 -17 289
25 -5 25 24 -9 81
26 -4 16 28 -5 25
32 +2 4 32 -1 01
34 +4 16 35 +2 04
38 +8 64 37 +4 16
40 +10 100 42 +9 81
42 +12 144 43 +10 100
45 +12 144
47 +14 196
𝑿a = 270 (𝑋 − 𝑿)𝟐
= 734 𝑿b = 363 (𝑋 − 𝑿)𝟐
= 1298
𝑿a =
𝟐𝟕𝟎
𝟗
= 30
𝑿b =
𝟑𝟔𝟑
𝟏𝟏
= 33
Prepared by: Bhavya S. Jaiswal

9. According to the formula,
𝑺𝟐 =
(𝑿−𝑿)
𝟐
𝑵−𝟏
than, 𝑆22 =
734
9−1
= 91.75
𝑆12 =
1298
11−1
= 129.8
So that, F=
𝑆12
𝑆22 =
129.8
91.75
= 𝟏. 𝟒𝟏𝟒𝟕
Now the tabulated value of F according to DOF1 and DOF2 = 3.35
Hence, the calculated F-value is lower than the Tabulated F-value than we can say
that the population has same variance.
Prepared by: Bhavya S. Jaiswal

10. S1
S2
S2
Prepared by: Bhavya S. Jaiswal

11. References
1. https://www.statisticshowto.com/probability-and-statistics/hypothesis-
testing/f-test/
2. https://blog.minitab.com/blog/adventures-in-statistics-2/understanding-
analysis-of-variance-anova-and-the-f-test
3. http://www.socr.ucla.edu/Applets.dir/F_Table.html
Prepared by: Bhavya S. Jaiswal