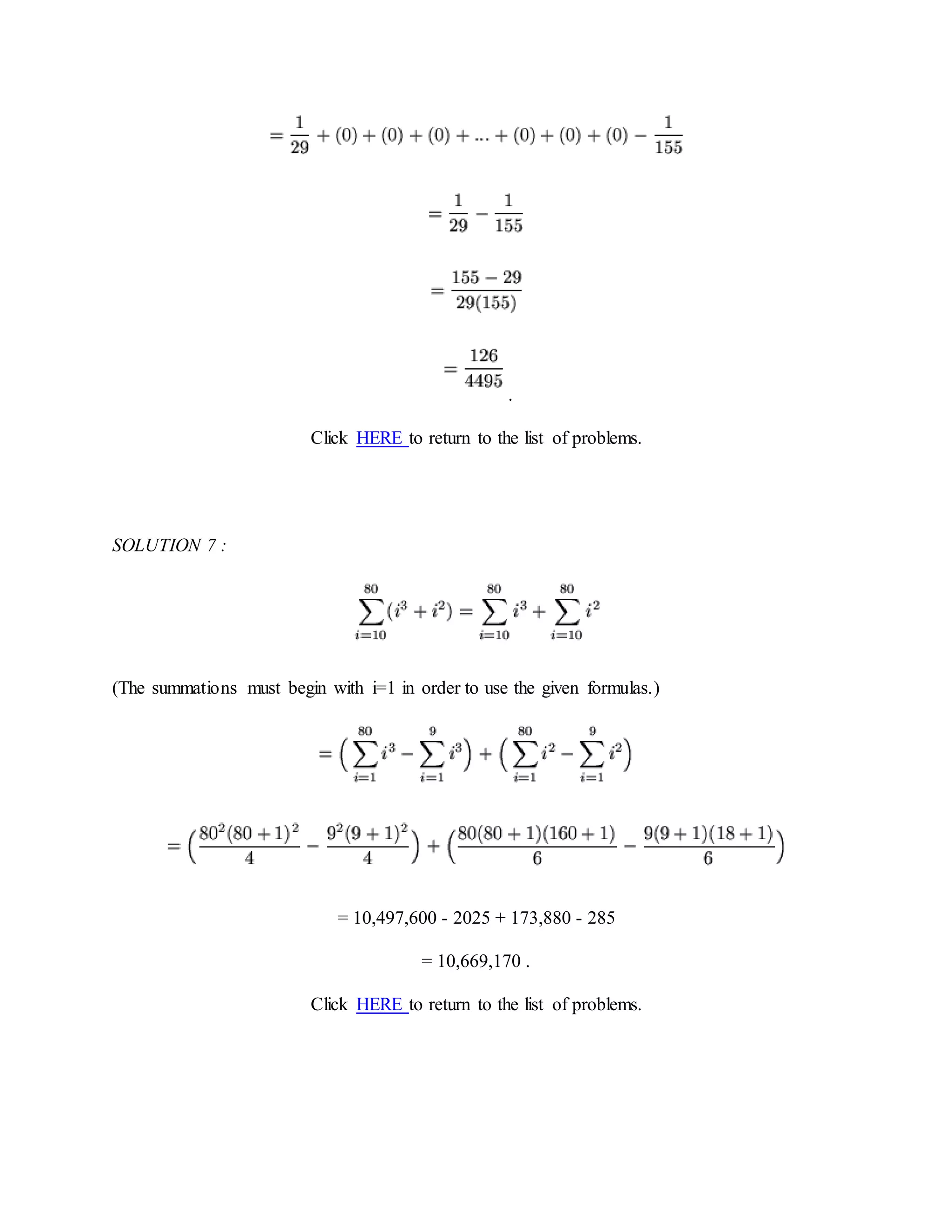
The document provides 14 solutions to algebra summation problems. Each solution shows the step-by-step working to evaluate summations using summation rules and properties like grouping like terms, factoring, and treating summations as telescoping sums where consecutive terms cancel out. Examples include evaluating summations of increasing powers and fractions that are decomposed into partial fractions to find a closed form solution.

1. SOLUTIONS TO THE ALGEBRA OF SUMMATION NOTATION
SOLUTION 1 :
= (5+1) + (5+2) + (5+4) + (5+8)
= 6 + 7 + 9 + 13
= 35 .
Click HERE to return to the list of problems.
SOLUTION 2 :
(The above step is nothing more than changing the order and grouping of the original
summation.)
(Placing 3 in front of the second summation is simply factoring 3 from each term in the
summation. Now apply Rule 1 to the first summation and Rule 2 to the second summation.)
= 400 + 15,150

2. = 15,550 .
Click HERE to return to the list of problems.
SOLUTION 3 :
(Separate this summation into three separate summations.)
(Factor out the number 6 in the second summation.)
(Apply Rules 1, 2, and 3.)
= 2,686,700 - 120,600 + 1800
= 2,567,900 .
Click HERE to return to the list of problems.
SOLUTION 4 :

3. (Since each summation begins with i=15, WE CANNOT USE THE RULES IN THE FORM
THAT THEY ARE GIVEN. Observe the following simple method to correct this shortcoming.)
(Now apply Rules 1 and 2.)
= 4(11,325 - 105) + (136)
= 45,016 .
Click HERE to return to the list of problems.
SOLUTION 5 :
(Note that cancels, then , then , then ... all the way to . Because of this
consecutive term cancellation, this type of summation is called a "telescoping" sum. This
cancellation will be shown in detail. First change the order of addition.)

4. (Now reassociate and collect "like" terms.)
(Recall that .)
.
Click HERE to return to the list of problems.
SOLUTION 6 :
(This is a "telescoping" sum. Group "like" terms and cancel.)

5. .
Click HERE to return to the list of problems.
SOLUTION 7 :
(The summations must begin with i=1 in order to use the given formulas.)
= 10,497,600 - 2025 + 173,880 - 285
= 10,669,170 .
Click HERE to return to the list of problems.

6. SOLUTION 8 :
(Recall that if n is an integer.)
(Recall that and
.)
= 1 + (-1) + 1 + (-1) + 1 + (-1) + 1 + (-1) + 1 + (-1)
= (1 + (-1)) + (1 + (-1)) + (1 + (-1)) + (1 + (-1)) + (1 + (-1))
= 0 + 0 + 0 + 0 + 0
= 0 .
Click HERE to return to the list of problems.
SOLUTION 9 :

7. = ( (-1) + 1 ) + ( (-1) + 1 ) + ... + ( (-1) + 1 ) + ( (-1) + 1 )
= 0 + 0 + ... + 0 + 0
= 0 .
Click HERE to return to the list of problems.
SOLUTION 10 :
There are several ways to prove that . This proof uses a telescoping sum.
Consider the summation . It can be evaluated in two different ways. First,
treat it as a telescoping sum. Then
(Commute the addition.)
= (-12 + 22) + (-22 + 32) + (-32 + 42) + (-42 + 52) + ... + (-(n-1)2 + n2) + (-n2 + (n+1)2)
(Group "like" terms.)
= -12 + (22 - 22) + (32 - 32) + (42 - 42) + (52 - 52) + ... + ((n-1)2-(n-1)2) + (n2 - n2) + (n+1)2
= -12 + (0) + (0) + (0) + (0) + ... + (0) + (0) + (n+1)2
= (n+1)2 - 1
= n2 + 2n + 1 - 1
(*)
= n2 + 2n .
Second,

8. (**)
.
Equating expressions (*) and (**) we get that
,
,
or
.
This completes the proof.

9. Click HERE to return to the list of problems.
SOLUTION 11 :
There are several ways to prove that . This proof uses a telescoping
sum. Consider the summation . It can be evaluated in two different ways.
First, treat it as a telescoping sum. Then
(Commute the addition.)
= (-13 + 23) + (-23 + 33) + (-33 + 43) + (-43 + 53) + ... + (-(n-1)3 + n3) + (-n3 + (n+1)3)
(Group "like" terms.)
= -13 + (23 - 23) + (33 - 33) + (43 - 43) + (53 - 53) + ... + ((n-1)3 - (n-1)3) + (n3 - n3) + (n+1)3
= -13 + (0) + (0) + (0) + (0) + ... + (0) + (0) + (n+1)3
= (n+1)3 - 1
= n3 + 3n2 + 3n + 1 - 1
(*)
= n3 + 3n2 + 3n .
Second,

10. (**)
.
Equating expressions (*) and (**) we get that
,
,
,
or

11. .
This completes the proof.
Click HERE to return to the list of problems.
SOLUTION 12 :
There is one nonobvious, but simple step in the solution of this problem. It requires that you
write a fraction as a sum or difference of partial fractions. For example,
is a partial fractions decomposition of . Then a partial fraction decomposition of is
so that
(This summation is a telescoping sum.)

12. (Now evaluate the limit.)
= 1 - 0
= 1 .
Click HERE to return to the list of problems.
SOLUTION 13 :
Note that in all of the following summations, letter i is a variable and letter n is a constant (until
the limit is evaluated). Then

13. (Now evaluate the limit.)
= 6 + (0) + 1 + (0) + (0)
= 7 .
Click HERE to return to the list of problems.
SOLUTION 14 :
The formula
4i -1 for i=1, 2, 3, 4, 5, ...
generates the given list of numbers. For example, the first number (i=1) in the list is
4(1)-1 = 3 .
The second number (i=2) in the list is

14. 4(2)-1 = 7 .
The 30th number (i=30) in the list is
4(30)-1 = 119 .
The 120th number (i=12) in the list is
4(120)-1 = 479 .
Thus, the sum of the first 120 numbers in this list can now be computed as
= 29,040 - 120
= 28,920 .