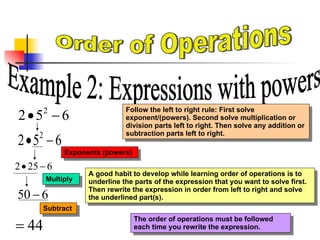
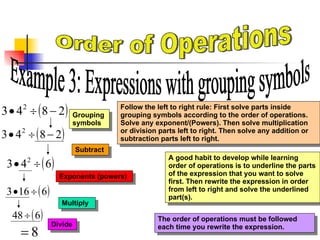
The document discusses the order of operations rules for evaluating arithmetic expressions. It explains that the order is: 1) operations within grouping symbols, 2) exponents, 3) multiplication and division from left to right, 4) addition and subtraction from left to right. Following the order of operations is important so that everyone calculates expressions the same way and achieves consistent results. The document provides examples of evaluating expressions with different operations like exponents, grouping symbols, and fractions.

1. Order Of Operations Rules for arithmetic and algebra expressions that describe what sequence to follow to evaluate an expression involving more than one operation . Step 1: First perform operations that are within grouping symbols such as parenthesis (), brackets [], and braces {}, and as indicated by fraction bars.Parenthesis within parenthesis are called nested parenthesis (( )). Step 2: Evaluate Powers ( exponents ) or roots . Step 3: Perform multiplication or division operations in order by reading the problem from left to right. Step 4: Perform addition or subtraction operations in order by reading the problem from left to right.

2. Order Of Operations Method 1 Method 2 Performing operations left to right only Performing operations using order of operations The rules for order of operations exist so that everyone can perform the same consistent operations and achieve the same results. Method 2 is the correct method. Can you imagine what it would be like if calculations were performed differently by various financial institutions or what if doctors prescribed different doses of medicine using the same formulas and achieving different results?

3. Order of operations Example 1: evaluate without grouping symbols Follow the left to right rule: First solve any multiplication or division parts left to right. Then solve any addition or subtraction parts left to right. A good habit to develop while learning order of operations is to underline the parts of the expression that you want to solve first. Then rewrite the expression in order from left to right and solve the underlined part(s). The order of operations must be followed each time you rewrite the expression. Divide Multiply Add

4. Order of Operations Example 2: Expressions with powers Exponents (powers) Multiply Subtract Follow the left to right rule: First solve exponent/(powers). Second solve multiplication or division parts left to right. Then solve any addition or subtraction parts left to right. A good habit to develop while learning order of operations is to underline the parts of the expression that you want to solve first. Then rewrite the expression in order from left to right and solve the underlined part(s). The order of operations must be followed each time you rewrite the expression.

5. Order of Operations Example 3: Expressions with grouping symbols Exponents (powers) Multiply Subtract Follow the left to right rule: First solve parts inside grouping symbols according to the order of operations. Solve any exponent/(Powers). Then solve multiplication or division parts left to right. Then solve any addition or subtraction parts left to right. A good habit to develop while learning order of operations is to underline the parts of the expression that you want to solve first. Then rewrite the expression in order from left to right and solve the underlined part(s). The order of operations must be followed each time you rewrite the expression. Grouping symbols Divide

6. Order of Operations Example 3: Expressions with fraction bars Exponents (powers) Multiply Subtract Follow the left to right rule: Follow the order of operations by working to solve the problem above the fraction bar. Then follow the order of operations by working to solve the problem below the fraction bar. Finally, recall that fractions are also division problems – simplify the fraction. A good habit to develop while learning order of operations is to underline the parts of the expression that you want to solve first. Then rewrite the expression in order from left to right and solve the underlined part(s). The order of operations must be followed each time you rewrite the expression. Work above the fraction bar Simplify: Divide Work below the fraction bar Grouping symbols Add

7. Order of Operations Example 3: Evaluating Variable Expressions Exponents (powers) 3 3 = (3)(3)(3) = 27 Subtract 29 - 5 A good habit to develop while learning order of operations is to underline the parts of the expression that you want to solve first. Then rewrite the expression in order from left to right and solve the underlined part(s). The order of operations must be followed each time you rewrite the expression. Grouping symbols Add: 2 + 27 Evaluate when x=2, y=3, and n=4 Substitute in the values for the variables Exponents (powers) 6 2 = (6)(6) = 36 Subtract 24 - 16 Add Follow the left to right rule: First solve parts inside grouping symbols according to the order of operations. Solve any exponent/(Powers). Then solve multiplication or division parts left to right. Then solve any addition or subtraction parts left to right.