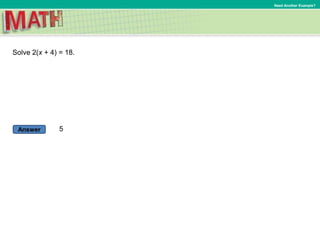
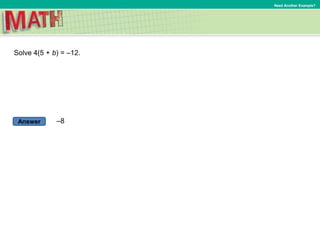
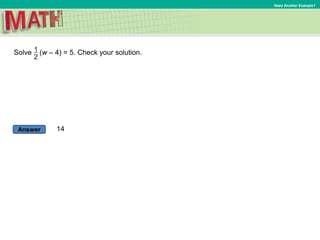
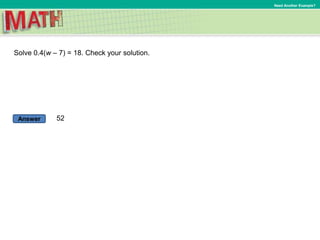
This document contains examples of solving equations with steps shown. It includes: 1) Five examples of solving equations of the form p(x+q)=r, showing the steps of writing the equation, using properties of equality to isolate the variable, and checking the solution. 2) An example of writing and solving an equation to find an unknown amount based on contextual information. 3) Questions asking how the content can help understand what it means for two quantities to be equal.

1. Solve each equation. Check your solution.
1. 4x + 8 = 32
2. 15 – 3a = 45
3. –9 + 7x = 68
4. –18 = –2m – 68
5. Four less than six times a number n is 32. Write and
solve an equation to find the number.
Course 2, Lesson 6-5

2. Course 2, Lesson 6-5
ANSWERS
1. x = 6
2. a = –10
3. x = 11
4. m = –25
5. 6n – 4 = 32; n = 6

3. WHAT does it mean to say
two quantities are equal?
Expressions and Equations
Course 2, Lesson 6-5

4. • 7.EE.4
Use variables to represent quantities in a real-world or mathematical
problem, and construct simple equations and inequalities to solve
problems by reasoning about the quantities.
• 7.EE.4a
Solve real-world problems leading to equations of the form px + q = r
and p(x + q) = r, where p, q, and r are specific rational numbers. Solve
equations of these forms fluently. Compare an algebraic solution to an
arithmetic solution, identifying the sequence of operations used in each
approach.
Course 2, Lesson 6-5 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and
Council of Chief State School Officers. All rights reserved.
Expressions and Equations

5. Mathematical Practices
1 Make sense of problems and persevere in solving them.
2 Reason abstractly and quantitatively.
3 Construct viable arguments and critique the reasoning of others.
4 Model with mathematics.
Course 2, Lesson 6-5 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and
Council of Chief State School Officers. All rights reserved.
Expressions and Equations

6. • To solve two-step equations in the
form p(x + q) = r
• To solve equations in the form
p(x + q) = r with rational coefficients
Course 2, Lesson 6-5
Expressions and Equations

7. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
1. Solve 3(x + 5) = 45.
Write the equation.3(x + 5) = 45
Division Property of Equality
– 5 = – 5
Simplify.x + 5 = 15
Subtraction Property of Equality
x = 10
=
Solve arithmetically.
Draw a bar diagram. From the diagram,
you can see that x + 5 = 45 ÷ 3 or 15.
So, x = 15 – 5 or 10.
Solve algebraically.
Simplify.

8. Answer
Need Another Example?
Solve 2(x + 4) = 18.
5

9. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
2. Solve 5(n – 2) = –30.
Write the equation.5(n – 2) = –30
Division Property of Equality
+ 2 = + 2
Simplify.
n = –4
Addition Property of Equality
Simplify. Check the solution.
n – 2 = –6

10. Answer
Need Another Example?
Solve 4(5 + b) = –12.
–8

11. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
3. Solve (n + 6) = 10. Check your solution.
Write the equation.(n + 6) = 10
Multiplication Property of Equality
–6 = –6
Simplify.
n = 9
Addition Property of Equality
Simplify.
n + 6 = 15
(n + 6) = 10
(n + 6) = • = 1; write 10 as .
5
1
Write the original equation.Check
?
Replace n with 9. Is this sentence true?
The sentence is true.
(9 + 6) = 10
10 = 10
(n + 6) = 10

12. Answer
Need Another Example?
Solve (w – 4) = 5. Check your solution.
14

13. 1
Need Another Example?
2
3
4
Step-by-Step Example
4. Solve 0.2(c – 3) = –10. Check your solution.
Write the equation.0.2(c – 3) = –10
Division Property of Equality
Simplify.
Addition Property of Equality
Simplify.
c – 3 = –50
Check 0.2(c – 3) = –10 Write the original equation.
?
The sentence is true.
Replace c with – 47.
Is this sentence true?
+3 = + 3
c = –47
0.2( –47 – 3) = –10
–10 = –10

14. Answer
Need Another Example?
Solve 0.4(w – 7) = 18. Check your solution.
52

15. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
5. Jamal and two cousins received the same amount of money
to go to a movie. Each boy spent $15. Afterward, the boys
had $30 altogether. Write and solve an equation to find the
amount of money each boy received.
Write the equation.
Let m represent the amount of money each boy received.
Simplify.
Addition Property of Equality
Simplify.
m – 15 = 10
So, each boy received $25.
3(m − 15) = 30
Division Property of Equality
+15 +15
m = 25

16. Answer
Need Another Example?
Javier bought 3 bags of balloons for a party. He used
8 balloons from each bag. Write and solve an equation
to find how many balloons were originally in each bag
if there were 21 balloons left over.
3(b – 8) = 21; 15 balloons

17. How did what you learned
today help you answer the
WHAT does it mean to say
two quantities are equal?
Course 2 Lesson 6-5
Expressions and Equations

18. How did what you learned
today help you answer the
WHAT does it mean to say
two quantities are equal?
Course 2 Lesson 6-5
Expressions and Equations
Sample answers:
• To solve two-step equations, such as 3(x + 2) = 9
• To solve two-step equations, such as (x + 2) = 9
1
3

19. The side length s + 3 of a square
with a perimeter of 52 inches
can be found using the equation
4(s + 3) = 52. What is the
side length of the square?
Ratios and Proportional RelationshipsExpressions and Equations
Course 2 Lesson 6-5