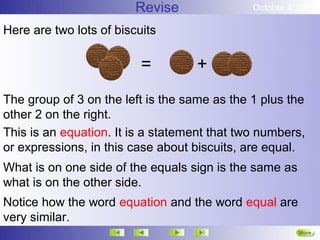
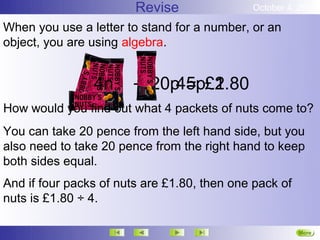
The document discusses equations with brackets and how to solve them. It provides examples of equations with brackets and explains the steps to solve them, which include: 1) Expanding the brackets by multiplying the terms inside by the number outside, 2) Performing the same operations to both sides of the equation to simplify it until the unknown variable is alone on one side. It also discusses solving equations where the unknown variable is on both sides of the equation.

1. October 4, 2012
Equations with brackets
1. Equations with brackets.
Next

2. Revise October 4, 2012
Here are two lots of biscuits
= +
The group of 3 on the left is the same as the 1 plus the
other 2 on the right.
This is an equation. It is a statement that two numbers,
or expressions, in this case about biscuits, are equal.
What is on one side of the equals sign is the same as
what is on the other side.
Notice how the word equation and the word equal are
very similar.
More
Next

3. Revise October 4, 2012
Here is another equation.
s+s+s =
Imagine we represented each snickers with the letter “s”.
3s =
You can work out what 1 snickers bar would cost by
dividing both sides of the equation by 3.
More
Next

4. Revise October 4, 2012
When you use a letter to stand for a number, or an
object, you are using algebra.
4n 45p£2
+n20p = £1.80
How would you find out what 4 packets of nuts come to?
You can take 20 pence from the left hand side, but you
also need to take 20 pence from the right hand to keep
both sides equal.
And if four packs of nuts are £1.80, then one pack of
nuts is £1.80 ÷ 4.
More
Next

5. Revise October 4, 2012
To solve an equation you need to simplify it until there is
a letter on one side of the equals sign and a number on
the other.
You do this by performing successive, operations to
each side of the equals sign.
Solve this simple equation 3x + 4 = 16
12
Take 4 from both sides. x=4
Divide both sides by 3.
You have used the opposite operation of “+ 4” and then
the opposite operation of “× 3”.
More
Next

6. Explanation October 4, 2012
Sometimes you need to solve an
equation that has brackets in it. 3(x + 2) = 12
First you need to expand the brackets.
This means multiply everything inside 3x + 6
the brackets by the number on the
outside.
Subtract 6 from both sides. 3x =6
Divide both sides by 3 x =2
Expanding the brackets first is the most reliable and
accurate way to solve an equation like this.
A quicker method is to start by dividing both sides by the
number outside the brackets. 3(x + 2) = 2
4
12
More
Next

7. Explanation October 4, 2012
When the unknown is on both sides.
You may need to solve an equation that has the
unknown on both sides. 3(x + 2) = x + 5
Start by expanding the brackets. 3 6
You can then work through the equation this way.
Subtract 6 from both sides. 3x = x -1
Subtract x from both sides 2x = -1
Divide both sides by 2. x = -0.5
After expanding the brackets, you could also proceed
through this equation by subtracting 5 from both sides,
or subtracting x from both sides.
More
Next
End