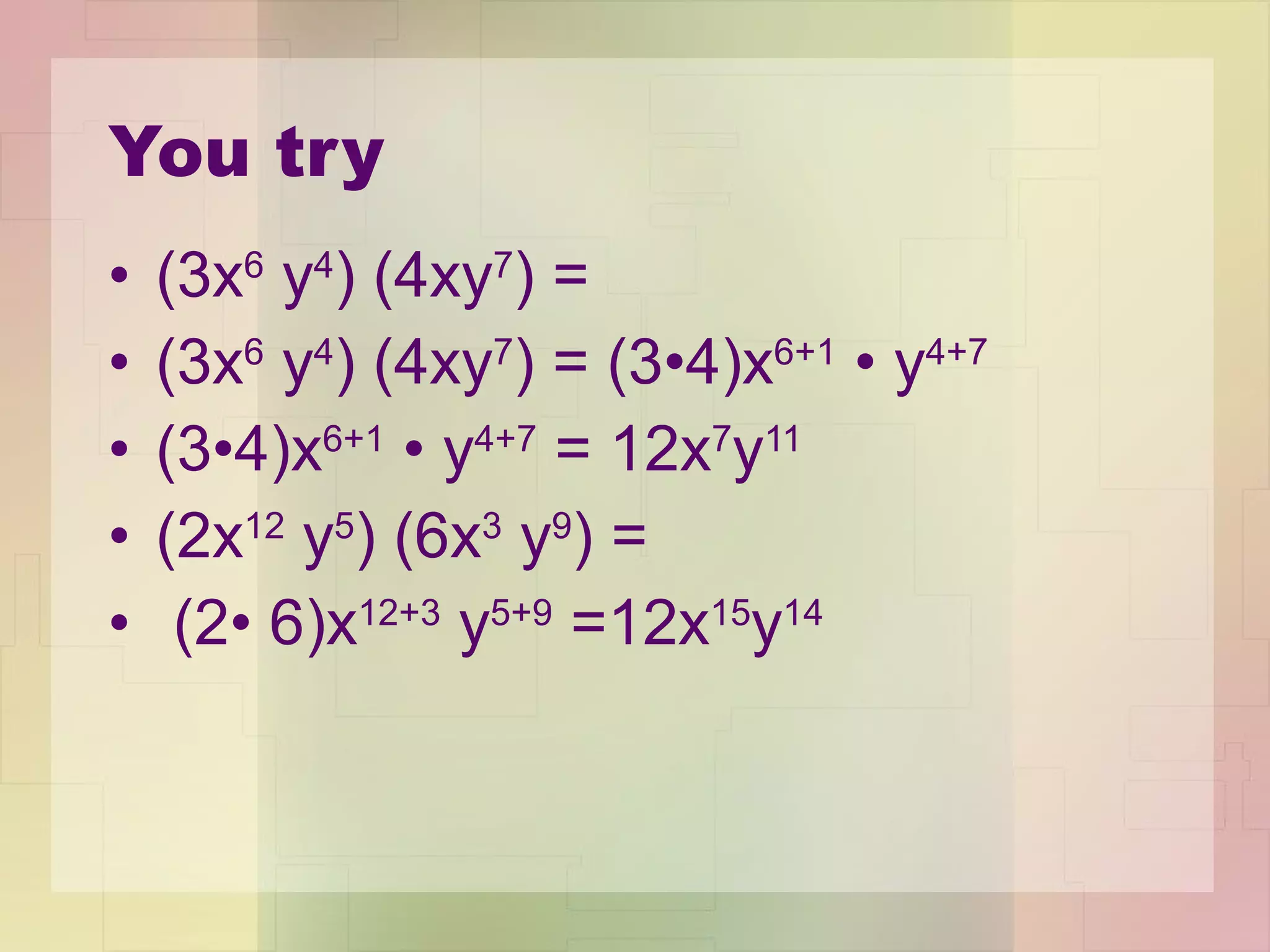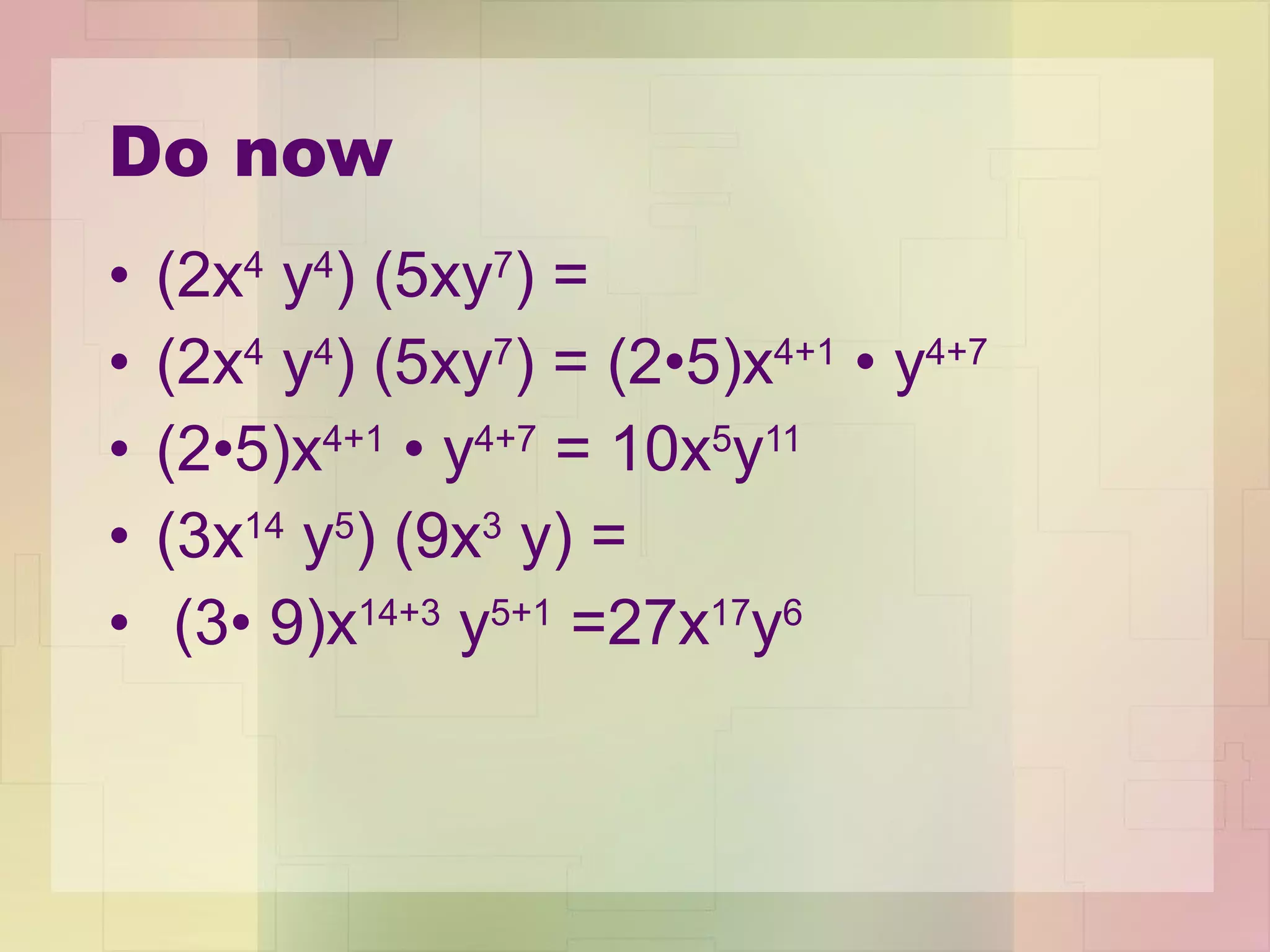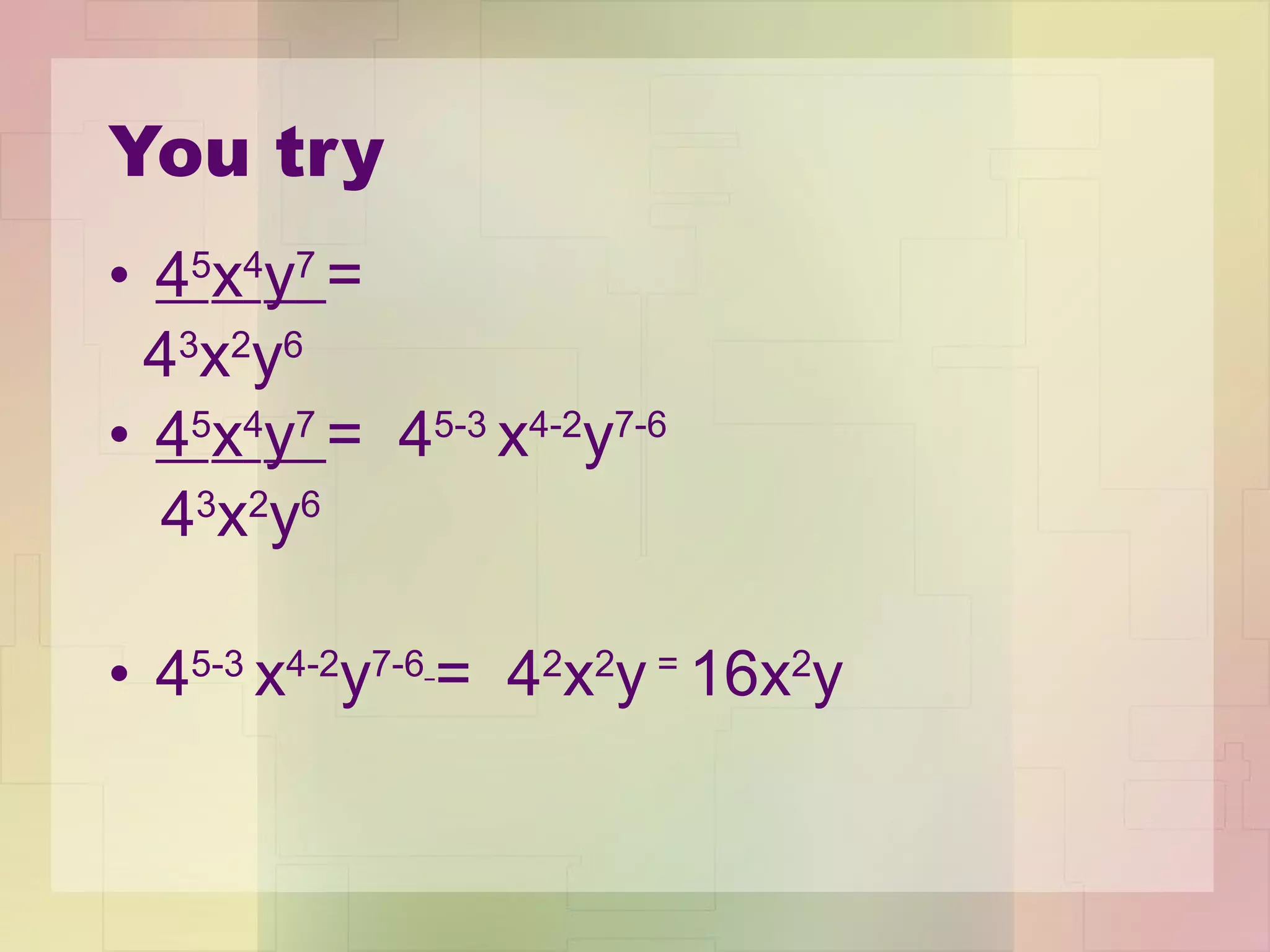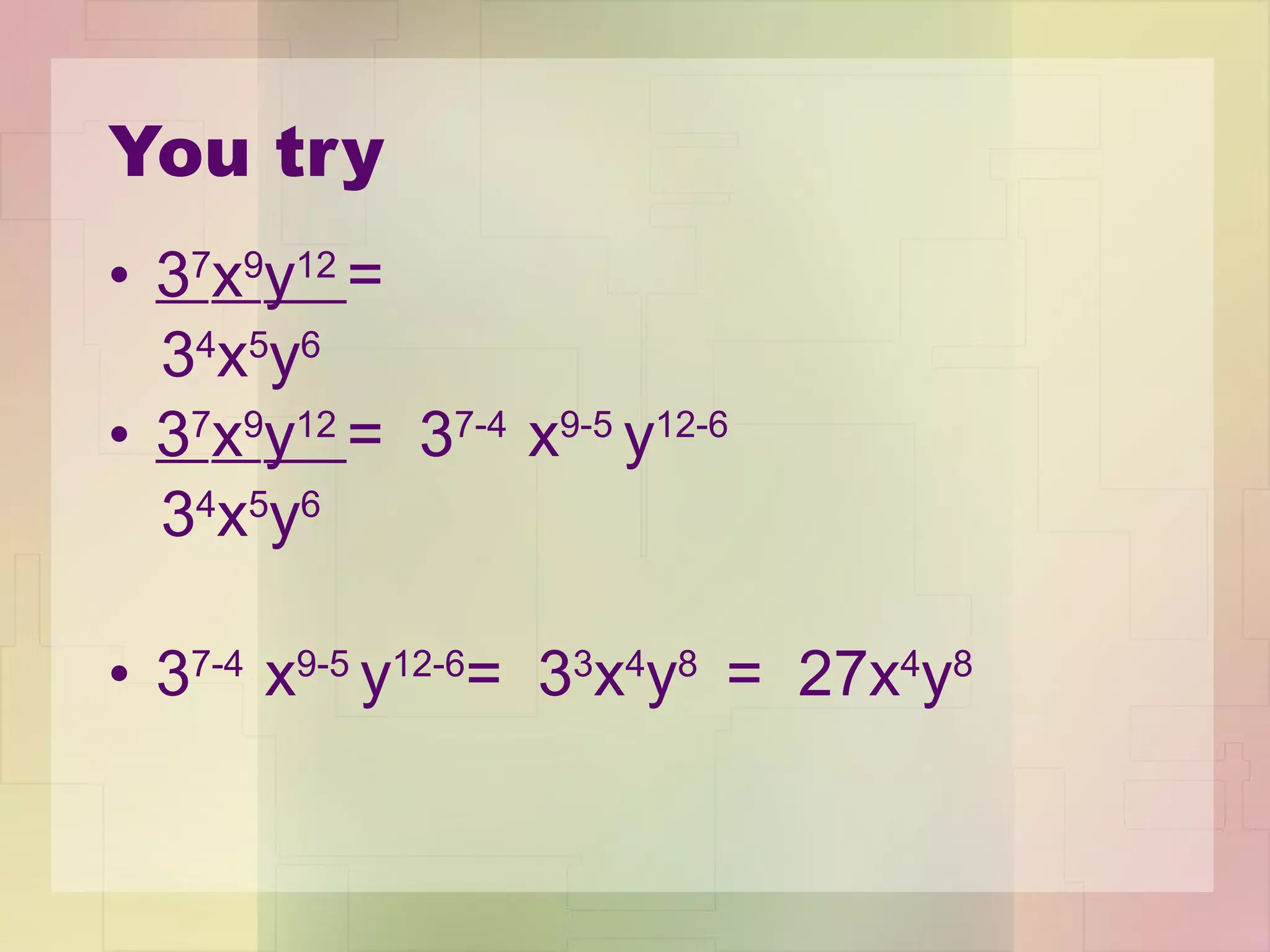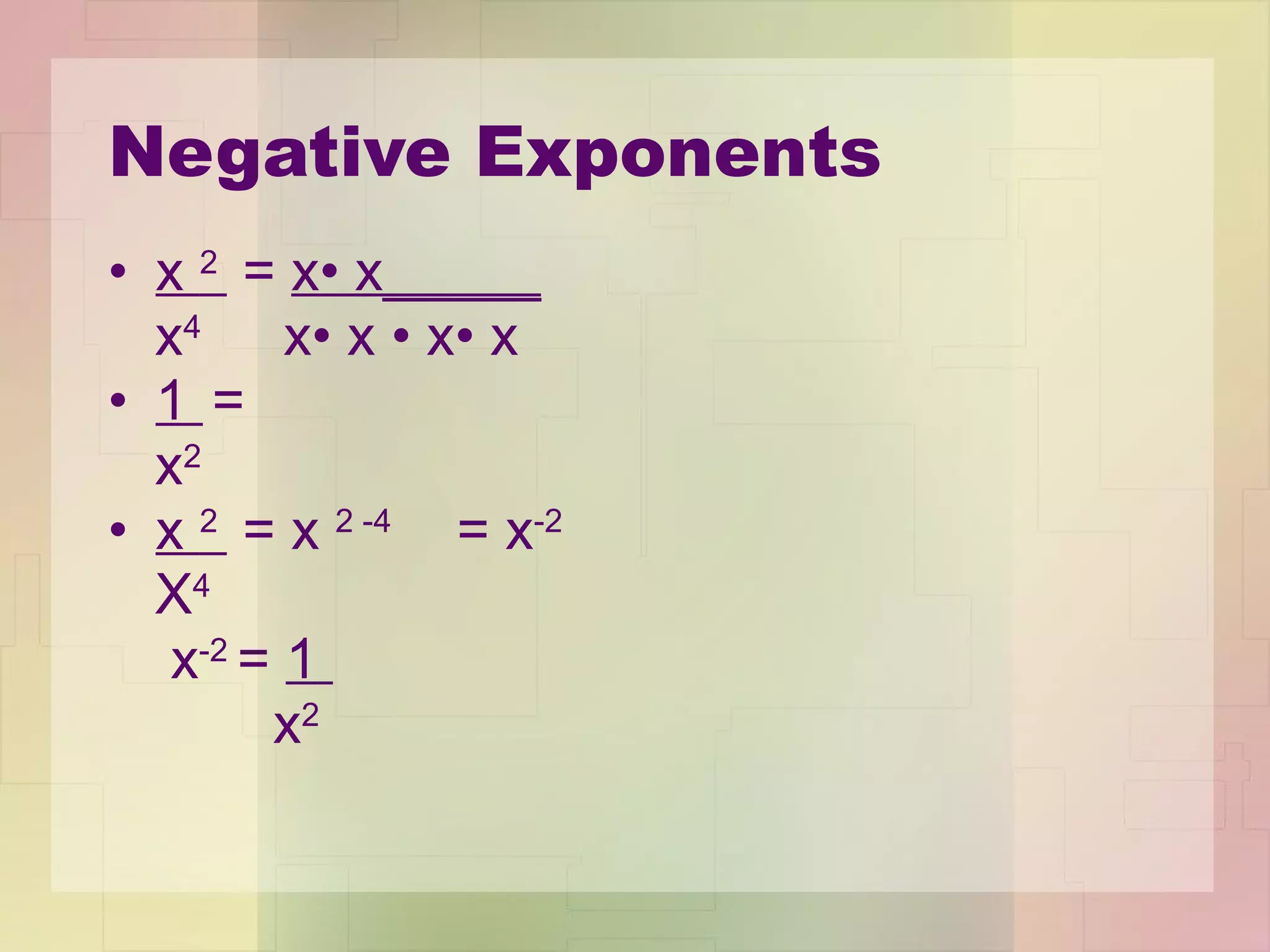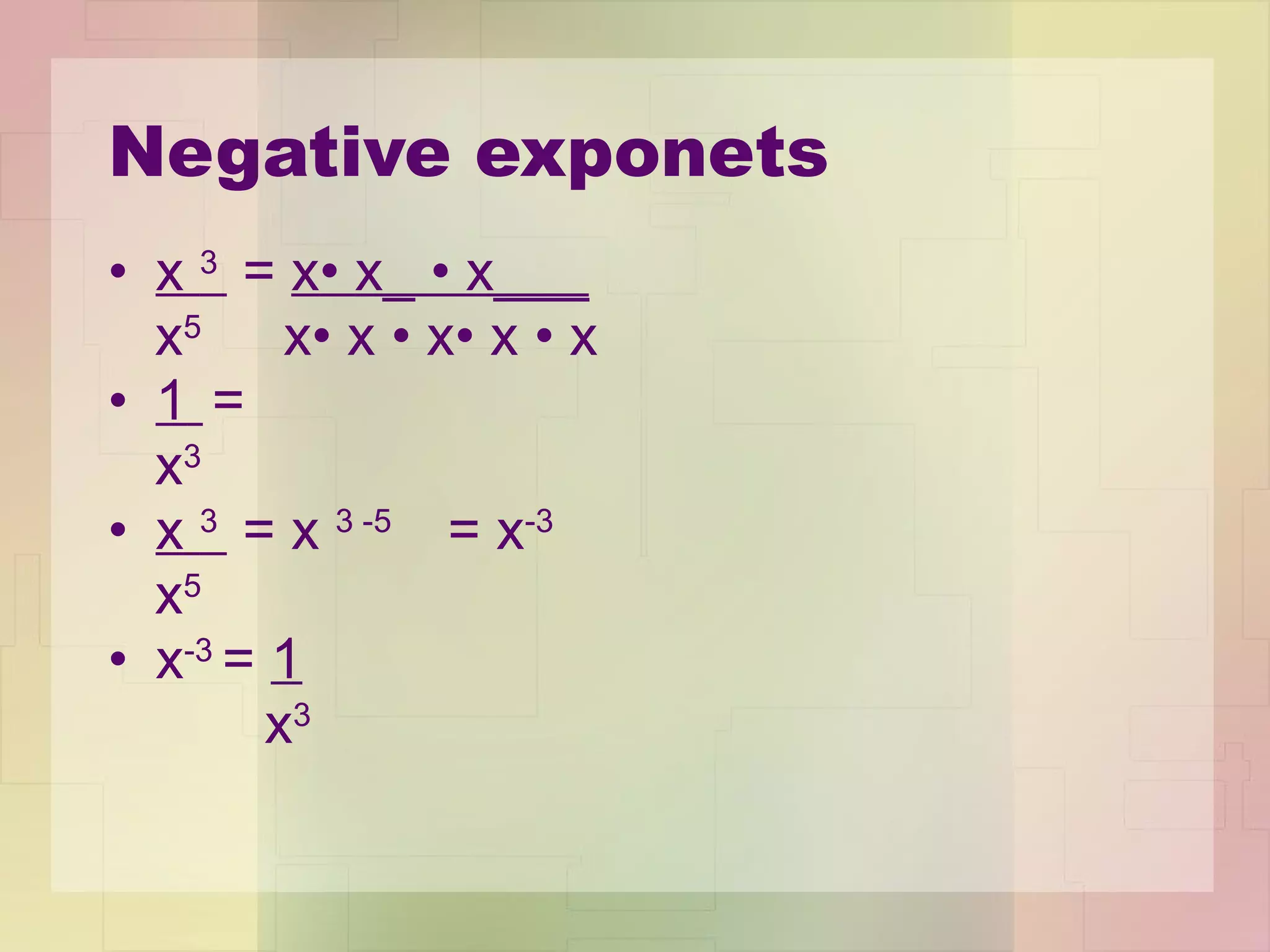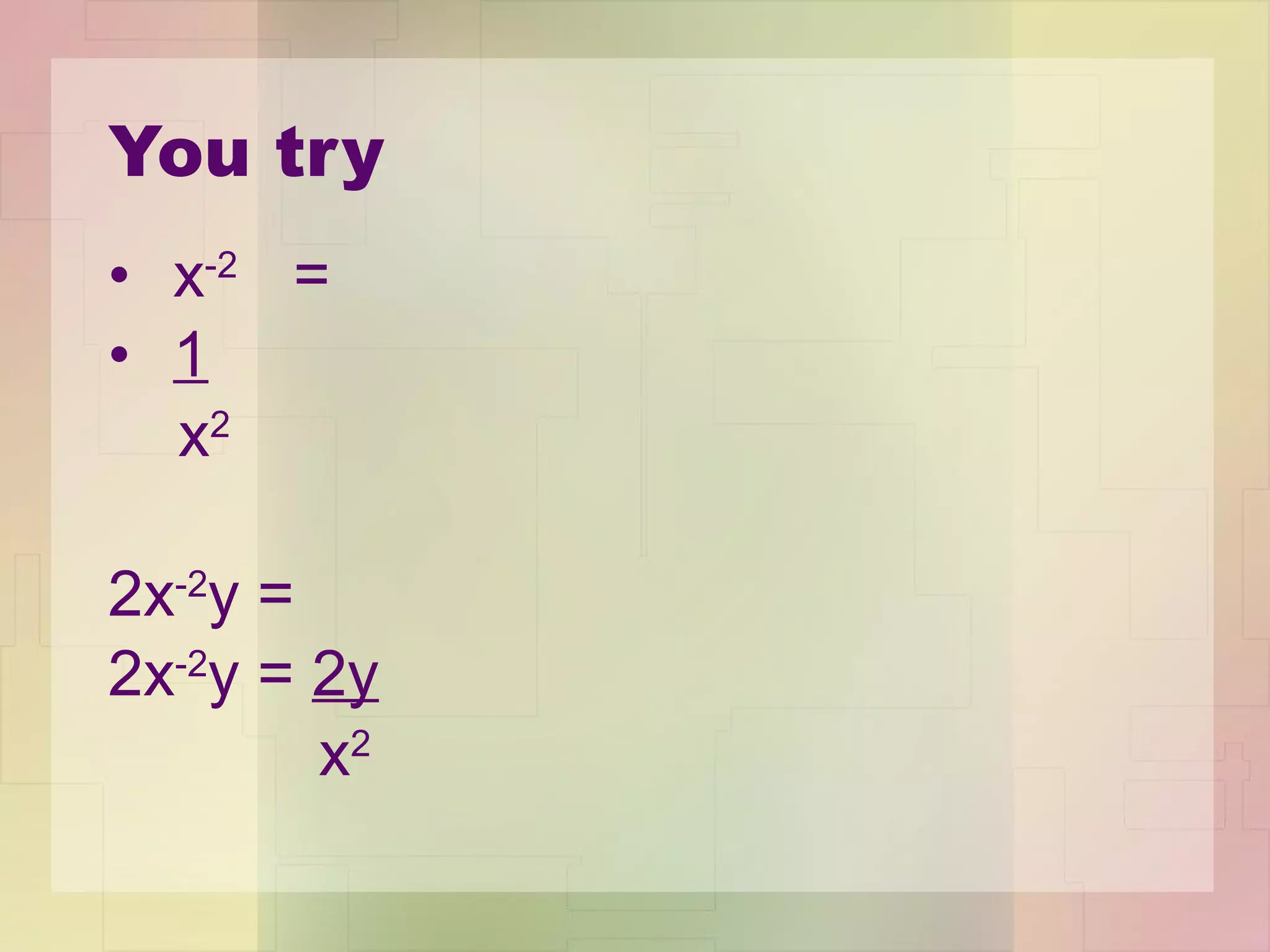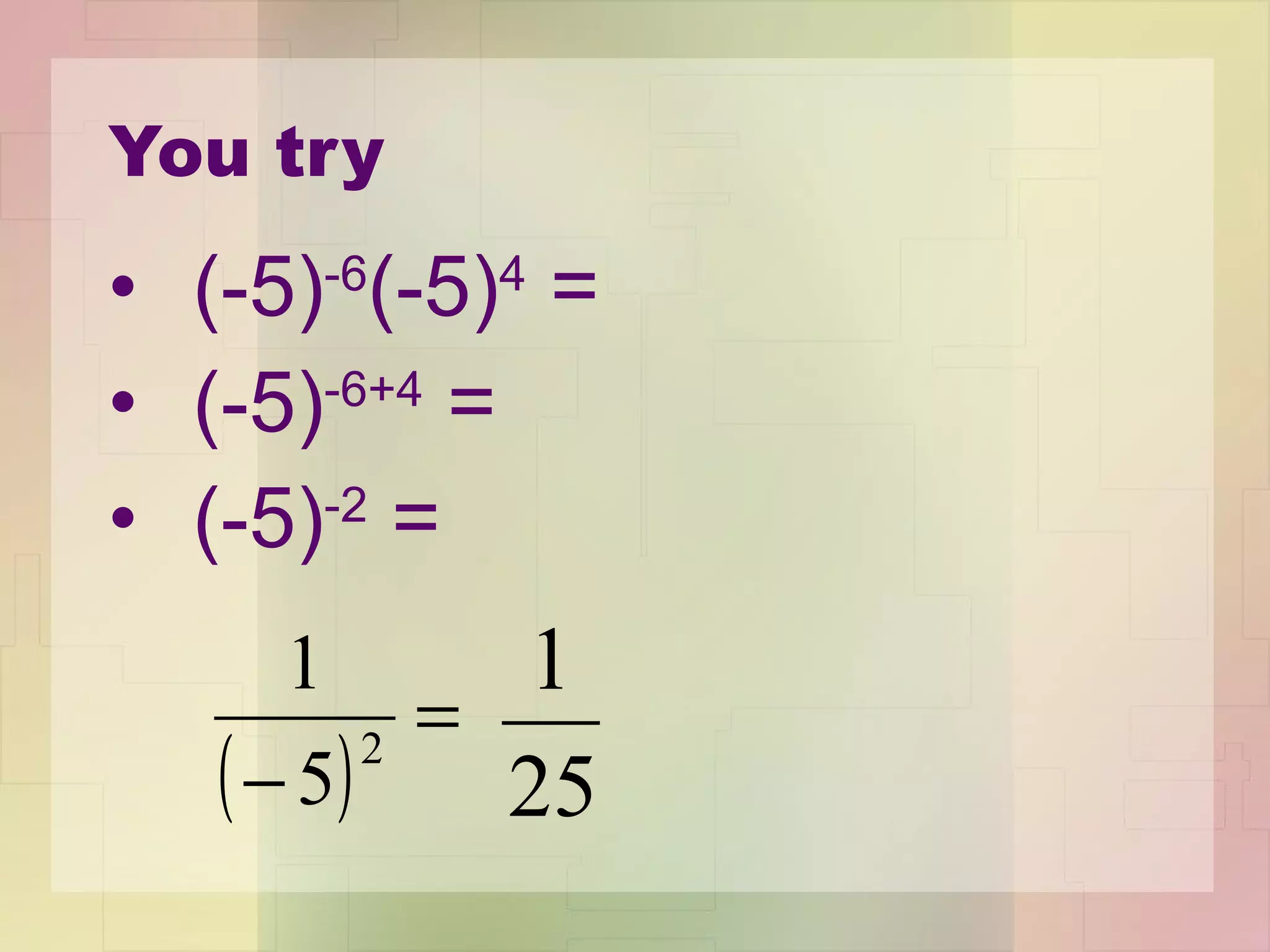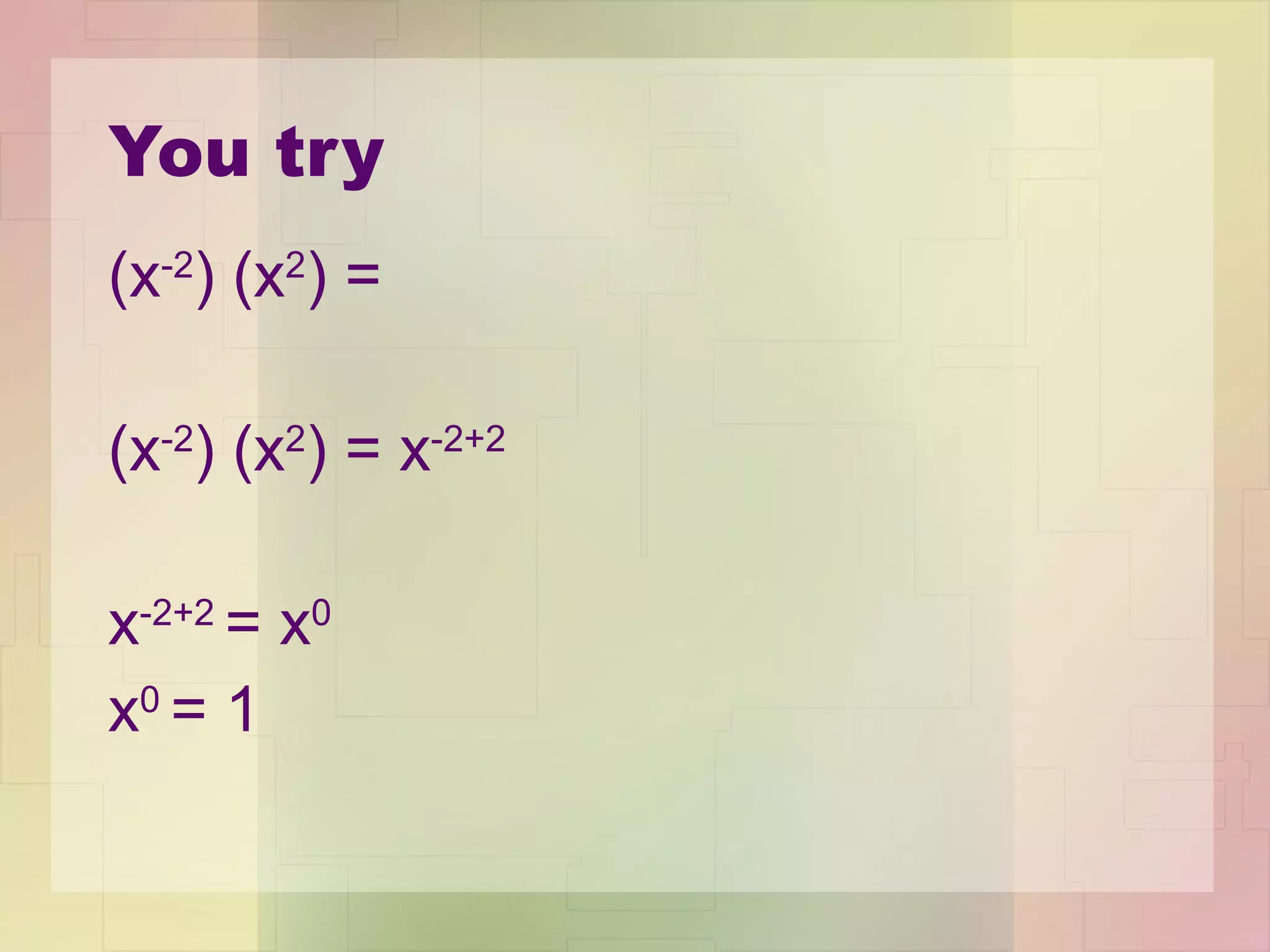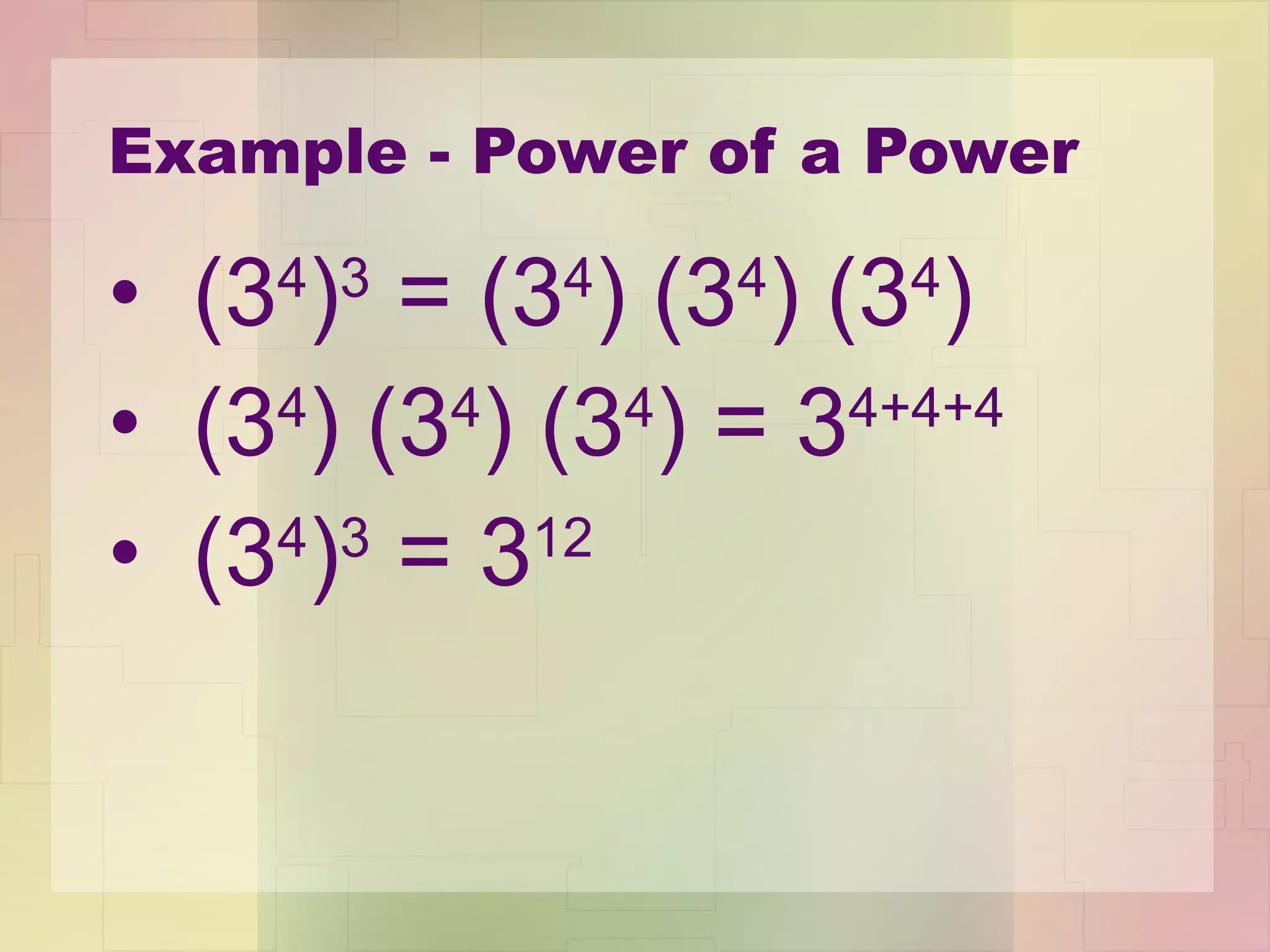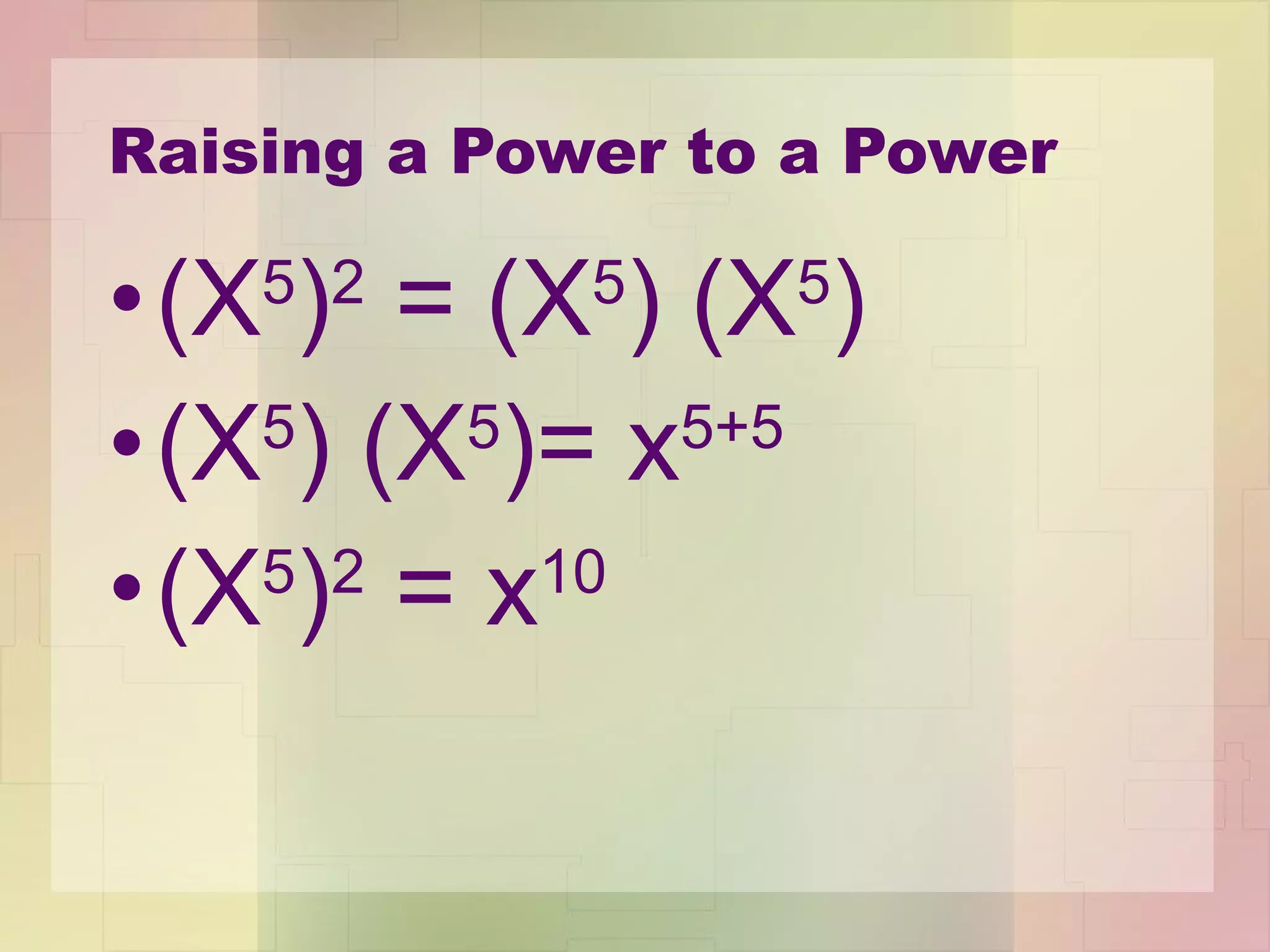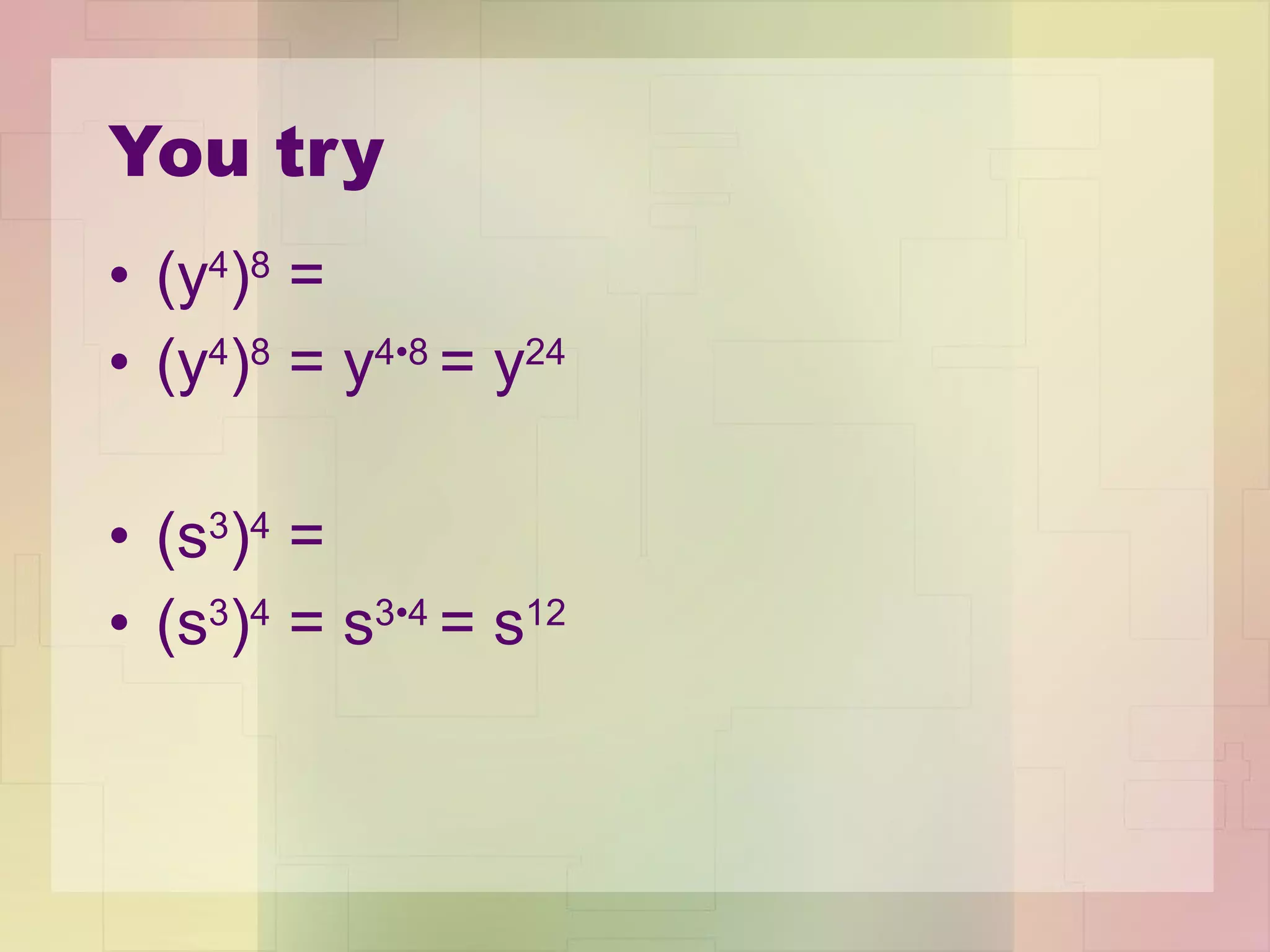The document summarizes several key properties of exponents: 1) The Product Property states that when multiplying like bases, you add the exponents. 2) The Quotient of Powers Property allows you to divide one power by another by subtracting the exponents. 3) The Power of a Power Property allows you to raise a power to another exponent by multiplying the exponents.

1. Properties of Exponents p. 323

2. Properties of Exponents a&b are real numbers, m&n are integers Product Property : Quotient of Powers : Power of a Power Property : Power of a Product Property : Negative Exponent Property : Zero Exponent Property : Power of Quotient:

3. Example – Product Property (-5) 3 (-5) 2 = (-5)(-5)(-5)(-5)(-5)= (-5) 5 (-5) 3+2 = (-5) 5

4. Example – Product Property x 5 • x 2 = x •x• x •x•x•x•x x 5+2 = x 7

5. Product Property a&b are real numbers, m&n are integers Product Property : (a m )(a n )=a m+n a 3 • a 5 • a 4 = a 3 • a 5 • a 4 = a 3+5+4 a 3 • a 5 • a 4 = a 12

6. Product Property (a 3 b 2 ) (a 4 b 6 ) = (a 3 a 4 ) (b 2 b 6 ) = a 3+4 b 2+6 a 3+4 b 2+6 = a 7 b 8 (x 5 y 2 ) (x 4 y 7 ) = (x 5 x 4 ) (y 2 y 7 ) = x 5+4 y 2+7 x 5+2 y 2+7 = x 9 y 9

7. You try (3x 6 y 4 ) (4xy 7 ) = (3x 6 y 4 ) (4xy 7 ) = (3 •4) x 6+1 • y 4+7 (3 •4) x 6+1 • y 4+7 = 12x 7 y 11 (2x 12 y 5 ) (6x 3 y 9 ) = (2 • 6) x 12+3 y 5+9 =12x 15 y 14

8. Do now (2x 4 y 4 ) (5xy 7 ) = (2x 4 y 4 ) (5xy 7 ) = (2 •5) x 4+1 • y 4+7 (2 •5) x 4+1 • y 4+7 = 10x 5 y 11 (3x 14 y 5 ) (9x 3 y) = (3 • 9) x 14+3 y 5+1 =27x 17 y 6

9. Dividing Powers with Like bases -5 3 = -5 • -5 • -5 -5 2 -5 • -5 -5 • -5 • -5 = -5 -5 • -5

10. Power of a Quotient with like bases x 4 = x • x • x • x X 2 x • x X 2

11. Quotient of Powers

12. Quotient of Powers Quotient of Powers : a m = a m-n ; a≠0 a n

13. You try 4 5 x 4 y 7 = 4 3 x 2 y 6 4 5 x 4 y 7 = 4 5-3 x 4-2 y 7-6 4 3 x 2 y 6 4 5-3 x 4-2 y 7-6 = 4 2 x 2 y = 16x 2 y

14. You try 3 7 x 9 y 12 = 3 4 x 5 y 6 3 7 x 9 y 12 = 3 7-4 x 9-5 y 12-6 3 4 x 5 y 6 3 7-4 x 9-5 y 12-6 = 3 3 x 4 y 8 = 27x 4 y 8

15. Negative Exponents x 2 = x • x_____ x 4 x • x • x • x 1 = x 2 x 2 = x 2 -4 = x -2 X 4 x -2 = 1 x 2

16. Negative exponets x 3 = x • x_ • x___ x 5 x • x • x • x • x 1 = x 3 x 3 = x 3 -5 = x -3 x 5 x -3 = 1 x 3

17. Example – Quotient of Powers

18. You try x -2 = 1 x 2 2x -2 y = 2x -2 y = 2y x 2

19. You try (-5) -6 (-5) 4 = (-5) -6+4 = (-5) -2 =

20. Properties of Exponents a&b are real numbers, m&n are integers Negative Exponent Property : a -m = ; a ≠0

21. Zero Exponent Property x 0 x 2 = x 2-2 x 2 x 2-2 = x 0 x 2 = 1 x 2 x 0 = 1

22. You try (x -2 ) (x 2 ) = (x -2 ) (x 2 ) = x -2+2 x -2+2 = x 0 x 0 = 1

23. Properties of Exponents a&b are real numbers, m&n are integers ets Review Zero Exponent Property : a 0 =1; a≠0

24. Properties of Exponents a&b are real numbers, m&n are integers Product Property : a m * a n =a m+n Quotient of Powers : a m = a m-n ; a≠0 a n Negative Exponent Property : a -m = ; a ≠0 Zero Exponent Property : a 0 =1; a≠0

25. Journal Entry: Describe the rules for the follwoing Product Property : Quotient of Powers : Negative Exponent Property : Zero Exponent Property :

26. Example – Power of a Power (2 3 ) 4 = (2 3 ) (2 3 ) (2 3 ) (2 3 ) 4 2 3+3+3+3 = (2 3 ) 4 = 2 12

27. Example - Power of a Power (3 4 ) 3 = (3 4 ) (3 4 ) (3 4 ) (3 4 ) (3 4 ) (3 4 ) = 3 4+4+4 (3 4 ) 3 = 3 12

28. Raising a Power to a Power (X 5 ) 2 = (X 5 ) (X 5 ) (X 5 ) (X 5 )= x 5+5 (X 5 ) 2 = x 10

29. Power of a Power Property a&b are real numbers, m&n are integers Power of a Power Property : (a m ) n =a mn (x 5 ) 3 = x 5 • 3 x 5 • 3 = x 15

30. You try (y 4 ) 8 = (y 4 ) 8 = y 4 •8 = y 24 (s 3 ) 4 = (s 3 ) 4 = s 3 •4 = s 12

31. Power of a Product Property (-2x 7 ) 2 = (-2x 7 ) (-2x 7 ) (-2x 7 ) (-2x 7 ) = (-2 • - 2) (x 7 • x 7 ) =4x 14 (-2x 7 ) 2 = (-2) 2 (x 7 ) 2 = -2 1 •2 x 7 • 2 = 4x 14

32. Power of a Product Property : (ab) m =a m b m (a 3 b 2 ) 4 = (a 3 ) 4 (b 2 ) 4 (a 3 ) 4 (b 2 ) 4 = a 3 •4 b 2 •4 =a 12 b 8

33. You try (-2x 4 ) 3 = (-2) 1 • 3 x 5 • 3 (-2x 4 ) 3 = (-2) 1 • 3 x 4 • 3 (-2) 1 • 3 x 4 • 3 = (-2) 3 x 12 = -16x 12 (4x 4 y 5 ) 2 (4x 4 y 5 ) 2 = 4 1 • 2 x 4 • 2 y 5 • 2 (4x 4 y 5 ) 2 = 16x 8 y 10

34. You try (-3x 5 y 3 ) 4 = (-3) 1 • 4 x 5 • 4 y 4 • 4 = (-3) 4 x 20 y 16 (7x 3 y -5 ) 2 7 1 • 2 x 3 • 2 y -5 • 2 16x 8 y -10 = 16x 8 y 10

35. Example – Power of Quotient

36. Properties of Exponents a&b are real numbers, m&n are integers Power of Quotient: b≠0

37. Properties of Exponents a&b are real numbers, m&n are integers Product Property : a m * a n =a m+n Quotient of Powers : a m = a m-n ; a≠0 a n Power of a Power Property : (a m ) n =a mn Power of a Product Property : (ab) m =a m b m Negative Exponent Property : a -m = ; a ≠0 Zero Exponent Property : a 0 =1; a≠0 Power of Quotient: b≠0

38. Multiplying and Dividing Monomials Monomial – an expression that is either a numeral, a variable or a product of numerals and variables with whole number exponents. Constant – Monomial that is a numeral. Example - 2

39. Journal Entry: Describe the rules for the follwoing Power of a Power Property : Power of a Product Property : Power of Quotient:

40. Multiplying Monomials (-2x 4 y 2 ) (-3xy 2 z 3 ) = (-2)(-3)(x 4 x )(y 2 y 2 ) z 3 6x 5 y 4 z 3 (-2x 3 y 4 ) 2 (-3xy 2 ) (-2 ) 2 x 3∙2 y 4∙2 ) (-3xy 2 ) (4)(-3)(x 6 x) (y 8 y 2 ) -12x 7 y 10

41. Scientific Notation A number is expressed in scientific notation when it is written as the product of a factor and a power of 10. The factor must be greater than or equal to 1 and less then 10 a x 10ⁿ, where 1 ≤ a < 10

42. Scientific Notation 131,400,000,000= 1.314 x 10 11 Move the decimal behind the 1 st number How many places did you have to move the decimal? Put that number here!

43. Write using scientific notation 12,300= 1.23 x 10 4 Write using standard notation 1.76 x 10 3 1,760

44. Example – Scientific Notation 131,400,000,000 = 5,284,000 1.314 x 10 11 = 5.284 x 10 6

45. Example – Scientific Notation (5.2 x 10 9 )(3.0 x 10 -3 )= (5.2 x 3.0) (10 9 x 10 -3 )= 15.6 x 10 6 1.56 x 10 7 2.45 x 10 -3 = 0.00245

46. Properties of Exponents a&b are real numbers, m&n are integers Product Property : a m * a n =a m+n Quotient of Powers : a m = a m-n ; a≠0 a n Power of a Power Property : (a m ) n =a mn Power of a Product Property : (ab) m =a m b m Negative Exponent Property : a -m = ; a ≠0 Zero Exponent Property : a 0 =1; a≠0 Power of Quotient: b≠0