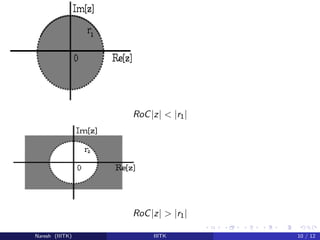
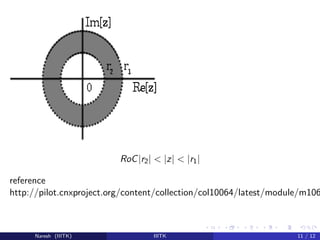
The document compares and contrasts the z-transform, Fourier series, and Fourier transform. 1) The z-transform is used for discrete-time signals, Fourier series is used for continuous periodic signals, and Fourier transform can be used for both discrete and continuous signals. 2) The z-transform converts difference equations to algebraic equations. Fourier series expands periodic functions as an infinite sum of sines and cosines. The Fourier transform provides a frequency representation of signals. 3) The inverse of the z-transform and Fourier transform are defined mathematically, while there is no inverse of a Fourier series since it does not change the domain of the original signal.

1. DIFFERENCE BETWEEN Z- TRANSFORM ,
FOURIER SERIES AND FOURIER TRANSFORM
Naresh Biloniya
2015KUEC2018
Department of Electronics and Communication Engineering
Indian Institute of Information Technology Kota
Naresh (IIITK) IIITK 1 / 12

2. Overview
1 Definition
2 Required Signal
3 Change In Signal
4 How To Apply Operation ?
5 Inverse
6 Other Differences
Naresh (IIITK) IIITK 2 / 12

3. Definition
The z-transform converts certain difference equations to algebraic
equations.
Ex. Z{yn} = Y(z)
A Fourier series is an expansion of a periodic function in terms of an
infinite sum of sines and cosines.
Fourier series make use of the orthogonality relationships of the sine
and cosine function.
The Fourier Transform provides a frequency domain representation of
time domain signals.
Ex. F{x(t)} = X(f)
Naresh (IIITK) IIITK 3 / 12

4. Required Signal
We use ZTransform for discrete time signal.
Ex. Unit impulse , unit step
x(n) = e−2n .
Fourier series is only applicable for continuous signal.
Ex. f(x) = x for −2 < x < 2
f(x) = sin(x) .
Fourier transform is applicable for discrete and continuous signal.
Ex. unit impulse , f(t) = e−t.
Naresh (IIITK) IIITK 4 / 12

5. Change In Signal
Z-transform converts a discrete-time signal, which is a sequence of
real or complex numbers, into a complex frequency domain
representation.
After Fourier series , a periodic signal remains periodic.
Ex. f(x) = x for −L <= x < L and the Fourier series of the function is
f (x) =
∞
x=0
Ancos(
nπx
L
) +
∞
n=1
Bnsin(
nπx
L
)
After Fourier transform , a non periodic signal becomes periodic.
f(x) = e−a|t| Fourier transform is
X(ω) =
2ω
a2 + ω2
Naresh (IIITK) IIITK 5 / 12

6. How To Apply Operation ?
The Z Transform of a sequence is defined as :
X(z) =
∞
n=−∞
x(n)z−n
The Fourier Transform of a function is defined as :
X(f ) =
∞
−∞
x(t)e−i2πft
dt
Naresh (IIITK) IIITK 6 / 12

7. Fourier Series of a function is defined as :
f (t) = a0 +
n=∞
n=1
anCos(nω0t) +
n=∞
n=0
bnSin(nω0t)
a0 =
1
T
T
0
f (t)dt
an =
2
T
T
0
f (t)Cos(nω0t)dt
bn =
2
T
T
0
f (t)Sin(nω0t)dt
reference
http://www.sosmath.com/fourier/fourier1/fourier1.html
Naresh (IIITK) IIITK 7 / 12

8. Inverse
The inverse Z - Transform of a function can be found by following
methods :
1. Direct division method
2. Partial fraction expansion method
3. Difference equation approach
4. MATLAB approach
The inverse of the Fourier Transform is defined as :
f (t) =
1
√
2π
∞
0
F(ω)eiωt
dt
There is no need to calculate inverse of Fourier series Because there is
no domain change .
Naresh (IIITK) IIITK 8 / 12

9. Other Differences
Fourier Transform is unique transform.It means magnitude of two
different function’s Fourier transform may be same but phase will
never be same.
RoC is calculated in Z - Transform to find out the stability.
For example : -
Naresh (IIITK) IIITK 9 / 12

10. RoC|z| < |r1|
RoC|z| > |r1|
Naresh (IIITK) IIITK 10 / 12

11. RoC|r2| < |z| < |r1|
reference
http://pilot.cnxproject.org/content/collection/col10064/latest/module/m106
Naresh (IIITK) IIITK 11 / 12

12. Thank you!
Questions and Suggestions
Nareshbiloniya123@gmail.com
Naresh (IIITK) IIITK 12 / 12