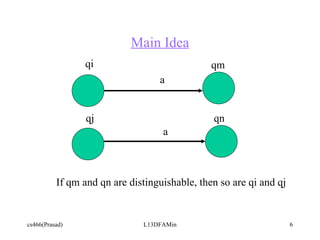
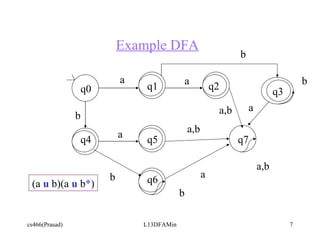
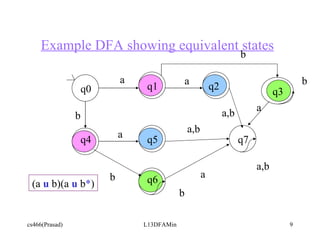
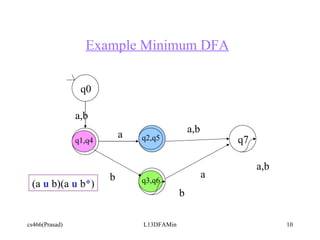
The document discusses determining equivalent states in a deterministic finite automaton (DFA) and using them to minimize the DFA. It provides an example of a DFA over the alphabet {a,b} recognizing strings with an even number of a's. The states {[Ea,Eb], [Ea,Ob]} and {[Oa,Eb], [Oa,Ob]} in this DFA are equivalent and can be collapsed into single states, creating a smaller minimal DFA with equivalent state partitions. The example DFA is then refined step-by-step to show the equivalent state partitions.

1. DFA Minimization

2. Strings over { a,b } with even number of a ’s  * Ea Oa Eb Ob Ob Eb b b b b a a a a [Oa,Ob] [Ea,Eb] [Ea,Ob] [Oa,Eb]

3. Strings over { a,b } with even number of a ’s  * Ea Oa a a [Ea] [Oa] b b

4. Observation The states among the state sets {[Ea,Eb], [Ea,Ob]} and {[Oa,Eb], [Oa,Ob]} differ on aspect immaterial for the problem at hand. Why not collapse these state sets into one state each, to get a smaller DFA?

5. Equivalent or Indistinguishable States Recall that a DFA state summarizes the substring consumed so far (that is, the past history). Two states qi and qj are equivalent or indistinguishable (for the future), if, when started in these states, every string causes the machine to either end up in an accepting state for both or end up in a non-accepting state for both. In other words, there is no string that can tell the equivalent states apart for the given language.

6. Main Idea qi qn qj qm If qm and qn are distinguishable, then so are qi and qj a a

7. Example DFA q0 q4 q1 q2 q3 q7 q5 q6 a b a a,b a a,b b b b a b (a u b)(a u b * ) a,b a

8. Refinement of State Partitions { {q0,q7} , {q1,q2,q3,q4,q5,q6} } { {q0},{q7}, {q1,q2,q3,q4,q5,q6} } On any transition { {q0},{q7}, {q1,q2,q3,q4,q5,q6} } { {q0},{q7}, {q1,q4}, {q2,q3,q5,q6} } On “a” transition { {q0},{q7}, {q1,q4}, {q2,q5},{q3,q6} } On “b” transition

9. Example DFA showing equivalent states q0 q4 q1 q2 q3 q7 q5 q6 a b a a,b a a,b b b b a b (a u b)(a u b * ) a,b a

10. Example Minimum DFA q0 q1,q4 q7 q2,q5 q3,q6 a a,b a a,b b a,b b (a u b)(a u b * )

11. For an efficient way of determining minimal DFA, see the details in Algorithm 5.7.2