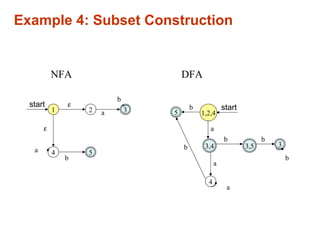
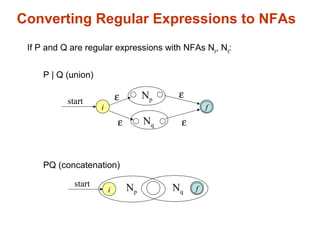
Thompson's construction algorithm converts regular expressions to nondeterministic finite automata (NFAs) by recursively building the NFA for each subexpression. The subset construction algorithm converts NFAs to deterministic finite automata (DFAs) by constructing states that correspond to sets of NFA states, and transitions correspond to the reachable states on each input symbol. Converting regular expressions to NFAs to DFAs shows that regular expressions, NFAs, and DFAs all have equivalent expressive power for describing regular languages.

1. Converting Regular Expressions to NFAs
• Empty string ε is a regular expression denoting { ε }
• a is a regular expression denoting {a} for any a in Σ
i ε fstart
i a fstart
Thompson’s Construction

2. Converting Regular Expressions to NFAs
If P and Q are regular expressions with NFAs Np, Nq:
P | Q (union)
PQ (concatenation)
Np
Nq
i f
ε
ε ε
ε
start
NqNpi f
start

3. Converting Regular Expressions to NFAs
If Q is a regular expression with NFA Nq:
Q* (closure)
ε
Nq f
ε
i
start ε
ε

4. Example (ab* | a*b)*
Starting with:
43
a*b b
a
startab* 1 2
a
b
start
1 2
a
43
5 6
ab* | a*b
ε
ε ε
ε
a
b
b
start

5. Example (ab* | a*b)*
1 2
a
43
5 6
ab* | a*b
ε
ε ε
ε
a
b
b
start
1 2
a
43
5 6
(ab* | a*b)*
7 8
ε
ε
ε ε
ε
ε ε
ε
b
b
a
start

6. Properties of Construction
1. N(r) has #of states ≤ 2*(#symbols + #operators) of r
2. N(r) has exactly one start and one accepting state
3. Each state of N(r) has at most one outgoing edge a∈Σ
or at most two outgoing ∈-transition
Let r be a regular expression, with NFA N(r), then

7. Detailed Example
r13
r12r5
r3 r11r4
r9
r10
r8r7
r6
r0
r1 r2
b
*
c
a a
|
( )
b
|
*
c
(ab*c) | (a(b|c*))
Parse Tree for this regular expression:
What is the NFA? Let’s construct it !

8. Detailed Example – Construction(1)
r3: a
r0: b
r2: c
b ∈
∈
∈
∈r1:
r4 : r1 r2
b ∈
∈
∈
∈ c
r5 : r3 r4
b ∈
∈
∈
∈a c
(ab*c) | (a(b|c*))

9. Detailed Example – Construction(2)
r11: a
r7: b
r6: c
c ∈
∈
∈
∈r9 : r7 | r8
∈
∈
b
r10 : r9
c ∈
∈
∈
∈r8:
c ∈
∈
∈
∈r12 : r11 r10
∈
∈
b
a
∈ ∈
∈ ∈
(ab*c) | (a(b|c*))

10. Detailed Example – Final Step
r13 : r5 | r12
b ∈
∈
∈
∈a c
c ∈
∈
∈
∈
∈
∈
b
a
∈
∈∈
∈
1
6543
8
2
10
9 12 13 14
11
15
7
16
17
∈∈

11. Converting NFAs to DFAs (subset
construction)
• Idea: Each state in the new DFA will correspond to
some set of states from the NFA. The DFA will be in
state {s0,s1,…} after input if the NFA could be in any of
these states for the same input.
• Input: NFA N with state set SN, alphabet Σ, start state sN,
final states FN, transition function TN: SN x {Σ U ε}  SN
• Output: DFA D with state set SD, alphabet Σ, start state
sD = ε-closure(sN), final states FD, transition function
TD: SD x Σ  SD

12. Terminology: ε-closure
ε-closure(T) = T + all NFA states reachable from any state in T
using only ε transitions.
1
5
2
43
b
ε
a ε
b
b
a
ε-closure({1,2,5}) = {1,2,5}
ε-closure({4}) = {1,4}
ε-closure({3}) = {1,3,4}
ε-closure({3,5}) = {1,3,4,5}

13. Illustrating Conversion – An Example
First we calculate: ∈-closure(0) (i.e., state 0)
∈-closure(0) = {0, 1, 2, 4, 7} (all states reachable from 0
on ∈-moves)
Let A={0, 1, 2, 4, 7} be a state of new DFA, D.
0 1
2 3
54
6 7 8 9
10
∈
∈
∈
∈
∈
∈
∈
∈ a
a
b
b
b
start
Start with NFA: (a | b)*abb
∈

14. Conversion Example – continued (1)
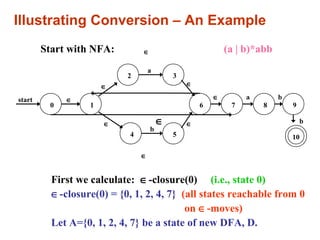
b : ∈-closure(move(A,b)) = ∈-closure(move({0,1,2,4,7},b))
adds {5} ( since move(4,b)=5)
From this we have : ∈-closure({5}) = {1,2,4,5,6,7}
(since 5→6 →1 →4, 6 →7, and 1 →2 all by ∈-moves)
Let C={1,2,4,5,6,7} be a new state. Define Dtran[A,b] = C.
2nd
, we calculate : a : ∈-closure(move(A,a)) and
b : ∈-closure(move(A,b))
a : ∈-closure(move(A,a)) = ∈-closure(move({0,1,2,4,7},a))}
adds {3,8} ( since move(2,a)=3 and move(7,a)=8)
From this we have : ∈-closure({3,8}) = {1,2,3,4,6,7,8}
(since 3→6 →1 →4, 6 →7, and 1 →2 all by ∈-moves)
Let B={1,2,3,4,6,7,8} be a new state. Define Dtran[A,a] = B.

15. Conversion Example – continued (2)
3rd
, we calculate for state B on {a,b}
a : ∈-closure(move(B,a)) = ∈-closure(move({1,2,3,4,6,7,8},a))}
= {1,2,3,4,6,7,8} = B
Define Dtran[B,a] = B.
b : ∈-closure(move(B,b)) = ∈-closure(move({1,2,3,4,6,7,8},b))}
= {1,2,4,5,6,7,9} = D
Define Dtran[B,b] = D.
4th
, we calculate for state C on {a,b}
a : ∈-closure(move(C,a)) = ∈-closure(move({1,2,4,5,6,7},a))}
= {1,2,3,4,6,7,8} = B
Define Dtran[C,a] = B.
b : ∈-closure(move(C,b)) = ∈-closure(move({1,2,4,5,6,7},b))}
= {1,2,4,5,6,7} = C
Define Dtran[C,b] = C.

16. Conversion Example – continued (3)
5th
, we calculate for state D on {a,b}
a : ∈-closure(move(D,a)) = ∈-closure(move({1,2,4,5,6,7,9},a))}
= {1,2,3,4,6,7,8} = B
Define Dtran[D,a] = B.
b : ∈-closure(move(D,b)) = ∈-closure(move({1,2,4,5,6,7,9},b))}
= {1,2,4,5,6,7,10} = E
Define Dtran[D,b] = E.
Finally, we calculate for state E on {a,b}
a : ∈-closure(move(E,a)) = ∈-closure(move({1,2,4,5,6,7,10},a))}
= {1,2,3,4,6,7,8} = B
Define Dtran[E,a] = B.
b : ∈-closure(move(E,b)) = ∈-closure(move({1,2,4,5,6,7,10},b))}
= {1,2,4,5,6,7} = C
Define Dtran[E,b] = C.

17. Conversion Example – continued (4)
Dstates
Input Symbol
a b
A B C
B B D
C B C
E B C
D B E
A
C
B D Estart bb
b
b
b
a
a
a
a
This gives the transition table Dtran for the DFA of:

18. Algorithm For Subset Construction
push all states in T onto stack;
initialize ∈-closure(T) to T;
while stack is not empty do begin
pop t, the top element, off the stack;
for each state u with edge from t to u labeled ∈ do
if u is not in ∈-closure(T) do begin
add u to ∈-closure(T) ;
push u onto stack
end
end
computing the
∈-closure

19. Algorithm For Subset Construction – (2)
initially, ∈-closure(s0) is only (unmarked) state in Dstates;
while there is unmarked state T in Dstates do begin
mark T;
for each input symbol a do begin
U := ∈-closure(move(T,a));
if U is not in Dstates then
add U as an unmarked state to Dstates;
Dtran[T,a] := U
end
end

20. Example 2: Subset Construction
NFA
1
5
2
43
ε
b
a b
a,b
a,b
start
NFA N with
• State set SN = {1,2,3,4,5},
• Alphabet Σ = {a,b}
• Start state sN=1,
• Final states FN={5},
• Transition function TN: SN x {Σ ∪ ε}  SN
a b ε
1 3 - 2
2 5 5, 4 -
3 - 4 -
4 5 5 -
5 - - -

21. Example 2: Subset Construction
NFA
1,2
T ∈-closure(move(T,
a))
∈-closure(move(T, b))
{1,2}
1
5
2
43
ε
b
a b
a,b
a,b
start
start

22. Example 2: Subset Construction
NFA
1,2 4,5
3,5
b
a
T ∈-closure(move(T,
a))
∈-closure(move(T, b))
{1,2} {3,5} {4,5}
{3,5}
{4,5}
1
5
2
43
ε
b
a b
a,b
a,b
start
start

23. Example 2: Subset Construction
1
5
2
43
ε
b
a b
a,b
a,b
NFA
1,2 4,5
3,5 4
b
a
b
T ∈-closure(move(T,
a))
∈-closure(move(T,
b))
{1,2} {3,5} {4,5}
{3,5} - {4}
{4,5}
{4}
start
start

24. Example 2: Subset Construction
1
5
2
43
ε
b
a b
a,b
a,b
NFA
1,2 4,5 5
3,5 4
a,bb
a
b
T ∈-closure(move(T,
a))
∈-closure(move(T, b))
{1,2} {3,5} {4,5}
{3,5} - {4}
{4,5} {5} {5}
{4}
{5}
start
start

25. Example 2: Subset Construction
1
5
2
43
ε
b
a b
a,b
a,b
NFA
1,2 4,5 5
3,5 4
a,b
a,b
b
a
b
T ∈-closure(move(T,
a))
∈-closure(move(T, b))
{1,2} {3,5} {4,5}
{3,5} - {4}
{4,5} {5} {5}
{4} {5} {5}
{5} - -
start
start

26. Example 2: Subset Construction
1
5
2
43
ε
b
a b
a,b
a,b
NFA
T ∈-closure(move(T,
a))
∈-closure(move(T, b))
{1,2} {3,5} {4,5}
{3,5} - {4}
{4,5} {5} {5}
{4} {5} {5}
{5} - -
All final states since the
NFA final state is included
start
1,2 4,5 5
3,5 4
a,b
a,b
b
a
b
start

27. Example 3: Subset Construction
1
5
2
43
b
ε
a b
b
a
NFA
ε
start

28. Example 3: Subset Construction
1
5
2
43
b
ε
a b
b
a
1 1,3,4
2
1,4,5
a
b
b
NFA DFA
ε
1,3,
4,5
a
a
a
b
b b
start start

29. Example 4: Subset Construction
1 2
54
ε
b
ε
1,2,4
NFA DFA
a
b
a 5
3,4 3,5
4
3
3
b
b
a
b
a
b
b
a
start start

30. Converting DFAs to REs
1. Combine serial links by concatenation
2. Combine parallel links by alternation
3. Remove self-loops by Kleene closure
4. Select a node (other than initial or final) for removal. Replace
it with a set of equivalent links whose path expressions
correspond to the in and out links
5. Repeat steps 1-4 until the graph consists of a single link
between the entry and exit nodes.

31. Example
1 2 3 4 5
6 7
d
a
b
c
d
0
d a
d bb
c
1 2 3 4 5
6 7
d a|b|c d
0
d a
d b
b|c
parallel edges become alternation
start
start
a
b
c

32. Example
3 4 5
d (a|b|c) d d
0
a
b (b|c) d
1 2 3 4 5
6 7
d a|b|c d
0
d a
d b
b|c
serial edges become concatenation
start
start

33. Example
3 4 5
d (a|b|c) d d
0
a
b (b|c) d
3 4 5
d (a|b|c) d d
0
a
b(b|c)da
Find paths that can be “shortened”
start
start

34. Example
3 4 5
d (a|b|c) d d
0
a
b(b|c)da
3 4 5
d (a|b|c) d (b(b|c)da)*d
0
a
5
d (a|b|c) d (b(b|c)da)*d
0
a
eliminate self-loops
serial edges become concatenation
start
start
start

35. Relationship among RE, NFA, DFA
• The set of strings recognized by an NFA can be described by a
Regular Expression.
• The set of strings described by a Regular Expression can be
recognized by an NFA.
• The set of strings recognized by an DFA can be described by a
Regular Expression.
• The set of strings described by a Regular Expression can be
recognized by an DFA.
• DFAs, NFAs, and Regular Expressions all have the same “power”.
They describe “Regular Sets” (“Regular Languages”)
• The DFA may have a lot more states than the NFA.