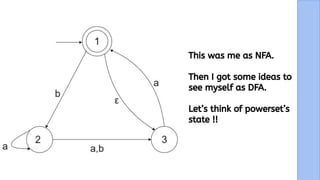
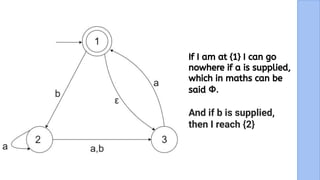
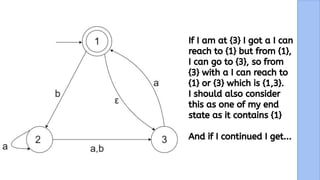
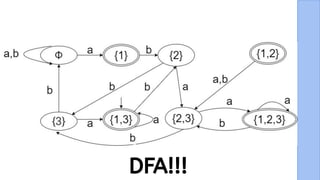
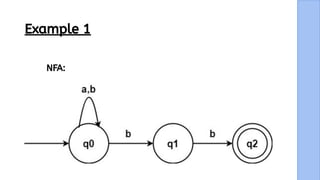
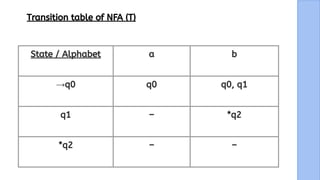
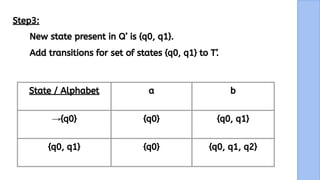
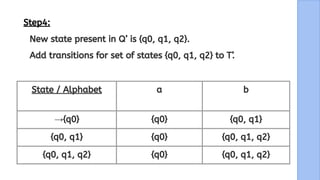
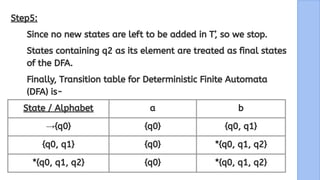
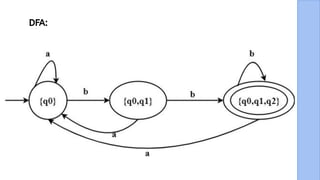
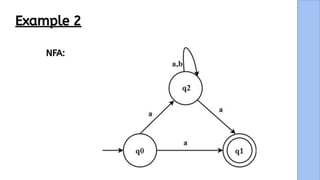
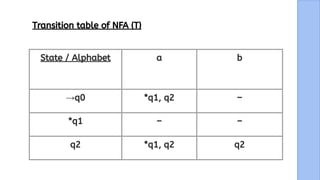
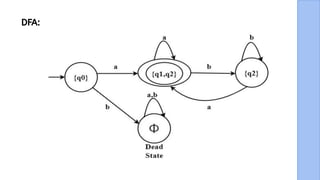
The document presents a detailed explanation of the equivalence between Non-Deterministic Finite Automata (NFA) and Deterministic Finite Automata (DFA) through a narrative framework. It outlines steps for converting an NFA to a DFA, including formal proofs and modifications for ε transitions. The presentation is collaborative and aims to illustrate the theoretical concepts in a relatable manner.

1. Lecture-10
NFA-DFA Equivalence Theorem
Group ID - 11
Prepared under CS222 at IIT Jodhpur

2. Contribution
Each person has contributed almost equally for this
presentation.
Whereas specific contributions include
Muskan Bathla(B18CSE036): 18 to 31
Nivedit Jain(B18CSE039): 1 to 9,16-17
Sanskar Mani(B18CSE048): 10 to 15
2

3. Hello!
I am NFA
I was very indecisive and confused about my
life…until yesterday….. when I attended Theory
of Computation lecture!
3

4. I realised that I am no less than DFA and
for every person of my kind, a DFA
counterpart exists!
I set onto a journey of finding my
counterpart…...

5. 5
This was me as NFA.
Then I got some ideas to
see myself as DFA.
Let’s think of powerset’s
state !!

6. 6
If I am at {1} I can go
nowhere if a is supplied,
which in maths can be
said Φ.
And if b is supplied,
then I reach {2}

7. 7
If I am at {3} I got a I can
reach to {1} but from {1},
I can go to {3}, so from
{3} with a I can reach to
{1} or {3} which is {1,3}.
I should also consider
this as one of my end
state as it contains {1}
And if I continued I get...

8. 8
DFA!!!

9. My Teacher helped me to realise it
formally.

10. 10
Proof Idea :
If a language is recognized by an NFA, then we must show
the existence of a DFA that also recognizes it. The idea is to
convert the NFA into an equivalent DFA that simulates the
NFA.
In NFA’s we keep track of the various states that we are
currently at. We simulate the string by transitioning all the
current states to using their transition function. Then we get
another set of states which we will then call our current
states.

11. 11
Proof Idea (2):
If k is the number of states of the NFA, it has 2k
subsets of
states. Each subset corresponds to one of the possibilities
that the DFA must remember, so the DFA simulating the NFA
will have 2k
states.
Logically analysing the start state should be the initial start
state and the final states should be the subsets containing
any one of the original final states as reaching any of them
would mean acceptance of the string.

12. 12
Formal Proof :
Let N = (Q, Σ, δ, q0
, F) be the NFA recognizing some
language A.
We construct a DFA M = (Q1
, Σ, δ1
, q0
1
F1
) recognizing A.
The steps below explain the construction for the case when
N is devoid of any ε transitions. We would be modifying the
construction later in order to take them into consideration.

13. 13
Formal Proof (2):
1. Q1
= P(Q).
Every state of M is a set of states of N. ( P(Q) if the set of
all subsets of Q or the power set of Q )
2. For R ∈ Q1
and a ∈ Σ, let δ1
(R, a) = {q ∈ Q| q ∈ δ(r, a)
for some r ∈ R}. When M reads a symbol a in state R, we
transition all of the states in the set R and transition to the
state in M containing exactly the states that we have
transitioned to. The transition function δ1
(R, a) could be
expressed formally as - δ1
(R, a) = Ur∈R
δ(r, a)

14. 14
Formal Proof (3):
3. q0
1
= {q0
}.
M starts in the state corresponding to the collection
containing just the start state of N.
4. F1
= {R ∈ Q1
| R contains an accept state of N}.
The machine M accepts if one of the possible states that N
could be in at this point is an accept state. The reason is to
accept any such string which might stop at any such states
which contain a final state of N.

15. 15
Formal Proof (4):
This would have been the end of the construction if there
were no ε transitions. The modification has been explained
in the following slide.
LETs see Modification!!

16. 16
We now need to consider the ε arrows. For any state R of
M, define E(R) to be the collection of states that can be
reached from members of R by going only along ε arrows,
including the members of R themselves so as to include all
the states of N which could be reached without reading the
string. Formally, for R ⊆ Q let E(R) = {q| q can be reached
from R by traveling along 0 or more ε arrows}.
Modification :

17. 17
Now we need to modify the transition function of M to take
into consideration all states that can be reached by going
along ε arrows after every step. Replacing δ(r, a) by E(δ(r,
a)) achieves this effect. Thus δ1
(R, a) = {q ∈ Q| q ∈ E(δ(r, a))
for some r ∈ R}.
We also need to modify the start state of M to all the
states that could be reached by q0
without reading the
string including itself. Changing q0
1
to be E({q0
}) achieves
this effect as this will include all the states that are
reachable without reading a string.
With this our construction is complete.
Modification :

18. 18
1. Let Q’ be the set of states of DFA.
Let T’ be the transition table of DFA.
2. Add start state of NFA to Q’ as the start state of DFA.
Add the transitions of start state to T’.
3. If any new state is present in T’
Add the new state in Q’.
Add transitions of that state in T’.
4. Keep repeating step 3 until no new state is present in T’.
Finally, the transition table T’ so obtained is the complete
transition table of the required DFA..
Steps for converting NFA to DFA

19. 19
Note Points:
1. The start state of DFA is unique and is same as the start
state of NFA.
2. *q represents the final state.
3. If any state makes transition to multiple states for some
input alphabet, then treat those multiple states as a single
state in the DFA.
4. The set of multiple states will be final state of DFA if it
contains a final state of the NFA.
5. In NFA, if the transition of any state over some input
alphabet is null,then perform the transition of that state
over that input alphabet to a dead state in the DFA.

20. 20
Example 1
NFA:

21. 21
State / Alphabet a b
→q0 q0 q0, q1
q1 – *q2
*q2 – –
Transition table of NFA (T)

22. 22
Step1:
Let Q’ be the set of states of DFA.
Let T’ be the transition table of DFA.
Step2:
Add transitions of start state q0 to T’
State / Alphabet a b
→{q0} {q0} {q0, q1}
Solution:

23. 23
Step3:
State / Alphabet a b
→{q0} {q0} {q0, q1}
{q0, q1} {q0} {q0, q1, q2}
New state present in Q’ is {q0, q1}.
Add transitions for set of states {q0, q1} to T’.

24. 24
Step4:
State / Alphabet a b
→{q0} {q0} {q0, q1}
{q0, q1} {q0} {q0, q1, q2}
{q0, q1, q2} {q0} {q0, q1, q2}
New state present in Q’ is {q0, q1, q2}.
Add transitions for set of states {q0, q1, q2} to T’.

25. 25
State / Alphabet a b
→{q0} {q0} {q0, q1}
{q0, q1} {q0} *{q0, q1, q2}
*{q0, q1, q2} {q0} *{q0, q1, q2}
Step5:
Since no new states are left to be added in T’, so we stop.
States containing q2 as its element are treated as final states
of the DFA.
Finally, Transition table for Deterministic Finite Automata
(DFA) is-

26. 26
DFA:

27. 27
Example 2
NFA:

28. 28
State / Alphabet a b
→q0 *q1, q2 –
*q1 – –
q2 *q1, q2 q2
Transition table of NFA (T)

29. 29
Solution:
Transition table of DFA (T’)
State / Alphabet a b
→{q0} *{q1, q2} Ø
*{q1, q2} *{q1, q2} {q2}
{q2} *{q1, q2} {q2}
Ø Ø Ø

30. 30
DFA:

31. ……..And this is how I found my DFA
counterpart!
Thank You for listening to the story of
my journey!