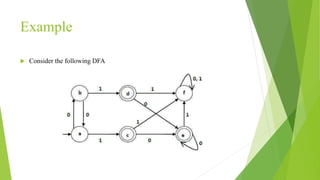
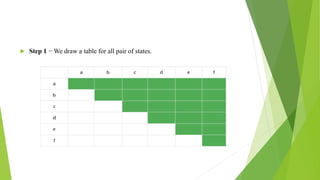
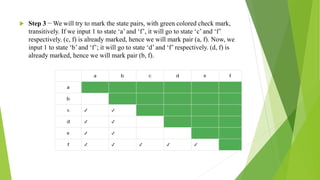
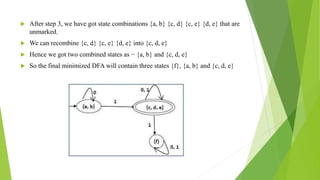
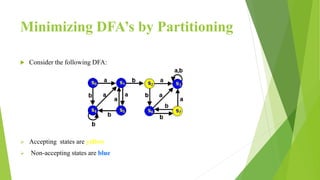
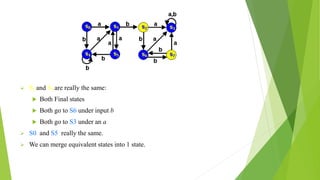
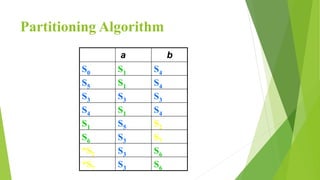
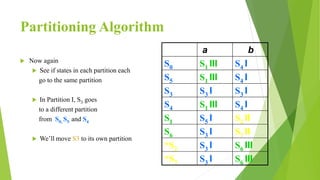
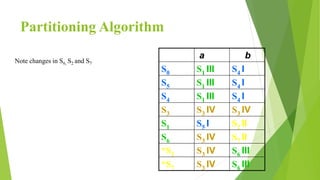
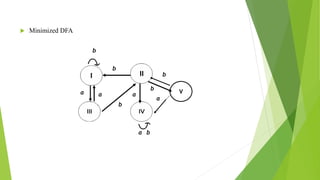
The document discusses methods for minimizing deterministic finite automata (DFAs). It explains that states can be eliminated if they are unreachable, dead, or non-distinguishable from other states. The partitioning algorithm is described as a method for finding equivalent states that go to the same partitions under all inputs. The algorithm is demonstrated on a sample DFA, merging equivalent states into single states until no further merges are possible, resulting in a minimized DFA. The Myhill-Nerode theorem provides another approach using a state pair marking technique to identify indistinguishable states that can be combined.








![Myphill-Nerode Theorem
Step 1 Draw a table for all pairs of states (Qi, Qj) not
necessarily connected directly [All are
unmarked initially]
Step 2 Consider every state pair (Qi, Qj) in the DFA
where Qi ∈ F and Qj ∉ F or vice versa and
mark them. [Here F is the set of final states].
Step 3 Repeat this step until we cannot mark
anymore states −
If there is an unmarked pair (Qi, Qj), mark it
if the pair {δ(Qi, A), δ (Qi, A)} is marked for
some input alphabet.
Step 4 Combine all the unmarked pair (Qi, Qj) and
make them a single state in the reduced DFA.](https://image.slidesharecdn.com/cd-160729103829/85/optimization-of-DFA-15-320.jpg)