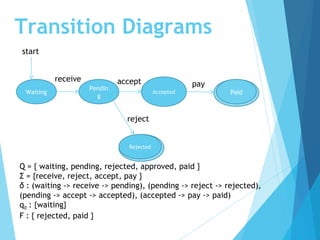
This document provides an overview of a seminar on finite automata. It discusses key topics including deterministic finite automata (DFA), non-deterministic finite automata (NFA), regular expressions, and regular languages. It defines these concepts, provides examples, and discusses applications such as text searching using regular expressions.

1. A Seminar
on
Finite Automata

2. Contents
 Deterministic Finite Automata
 Language
 Non – Deterministic Finite
Automata
 NFA to DFA Conversion
 Regular Expression
 Equality of Language
 Application of Regular Expression
 Regular Language

3. Deterministic Finite
Automata
 A system with many states
 Can transition from one state to
another with one input only
 Set of states is finite
 System is in one state at any given
time

4. DFA
Mathematical Definition of a DFA
A = (Q, Σ, δ, q0, F)
Q : Set of States, DFA is in one of these finite states at any time.
Σ : Set of Input symbols, DFA changes its state from one state to
another state on consuming an input symbol.
δ : Transition function.
 Function over δ=Q x Σ -> Q.
q0 : Initial DFA state
F : Final state. Once DFA reaches one of these states, it may not accept
any more input symbols.

5. DFA Example
Q(total states) = { waiting, pending, rejected,
approved, paid }
Σ(input alphabet) = {receive, reject, accept, pay }
δ(transition) : (waiting -> receive -> pending),
(pending -> reject -> rejected), (pending -> accept ->
accepted), (accepted -> pay -> paid)
Q0(Start state): {waiting}
F(final state) : { rejected, paid }

6. Paid
Paid
Transition Diagrams
Waiting
Pendin
g
Accepted Paid
Rejected
start
receive
reject
accept pay
Q = { waiting, pending, rejected, approved, paid }
Σ = {receive, reject, accept, pay }
δ : (waiting -> receive -> pending), (pending -> reject -> rejected),
(pending -> accept -> accepted), (accepted -> pay -> paid)
q0 : {waiting}
F : { rejected, paid }

7. Language
 Set of alphabets is called a String
 Set of Strings is called a Language
 A subset of strings is a language
 A DFA defines a language
 Alphabet set is the set of input symbol
Concatenation - one symbol follows another

8. Non-deterministic Finite
Automata (NDFA)
 An NFA is a five-tuple:
M = (Q, Σ, δ, q0, F)
Q A finite set of states
Σ A finite input alphabet
q0 The initial/starting state, q0 is in Q
F A set of final/accepting states, which is a subset of
Q
δ A transition function, which is a total function from
Q x Σ to 2Q

9. Example #1: one or more 0’s followed by
one or more 1’s
Q = {q0, q1, q2}
Σ = {0, 1}
Start state is q0
F = {q2}
δ: 0 1
q0
q1
q2
{q0, q1} {}
{} {q1, q2}
{q2} {q2}
q1
q0
q2
0 1
0 1
0/1

10. Why non – determinism is
useful?
Compressed information
Non-determinism hides backtracking
Programming languages, e.g., Prolog,
hides backtracking => Easy to program at a
higher level: what we want to do, rather
than how to do it
Useful in algorithm complexity study

11. NFA to DFA conversion
 For an NFA, N = {Q, Σ, δ, q0, F},
 Construct the DFA, D = {Qd, Σ, δd, {q0}, Fd}
 Qd = Powerset of Q
 δd(S, a) = Up in S δ(p,a) for every S in Qd.
 Fd = S : S is subset of Q and S has an accepting state of
NFA
 DFA operates on one state at a time, NFA operates on
sets of states.
 Given a state, NFA gives a set of new states
 Make all possible sets of DFA states as NFA states
 Transit from one set of states to a new set of all
possible state set

12. Regular Expression
 Algebraic expression to denote languages
 Composed of symbols “ε”, “Ø”, “+”, “*”, “.”, “(“,
“)” and alphabets
 The language is generated using rules :
 L(ε) = empty set
 L(Ø) = empty set
 L(a) = a for all alphabets a
 L(p+q) = L(p) U L(q)
 L(p.q) = { p’.q’ | p’ in L(p) & q’ in L(q) }
 L(p*
) = { qn
| q in L(p) and n >= 0 }, q0= ε, qk
=q.qk-1

13. Regular Expression
Example
#1. a+b.c
The language generated is :
{ a, b.c }
#2. a.b.c*
.d
the language generated is :
{ a.b.d, a.b.c.d, a.b.c.c.d, a.b.c.c.c.d, … }

14. Equality of Languages
 Two regular expression (or
automaton) are EQUAL if they
both generate same languages
Thus
(a.b)* + (b.a)* + a.(b.a)* + b.(b.a)*
= (ε + b).(a.b)*.(ε+a)

15. Applications of Regular
Expression
 Unix text search, search matching patterns (grep)
 Lexical/Parser analysis
 Parse text against a regular expression
 find set of first tokens at this expression root
 find set of last tokens at this expression root
 can the expression at this root be null set
 find set of next tokens after an alphabet
position in a regular expression
 Efficient search of patterns in very large repository
(web text search)

16. Regular Language
 A language (a set of strings) is
defined to be a regular language if
it can be defined by a finite
automaton
by a DFA or
by an NFA or
by an ε-NFA or
by a regular expression

17. References
 http://patentimage.storage.googleapis.com
 www.tutorialspoint.com/finite_automation.htm
 https://en.m.Wikipedia.org/wiki/finite_autom
ata.html