Recommended
PDF
PDF
PDF
PDF
PDF
PPTX
(実験心理学徒だけど)一般化線形混合モデルを使ってみた
PDF
PDF
StanとRでベイズ統計モデリング読書会 導入編(1章~3章)
PDF
PPTX
PPTX
PDF
臨床疫学研究における傾向スコア分析の使い⽅ 〜観察研究における治療効果研究〜
PPTX
Rで因子分析 商用ソフトで実行できない因子分析のあれこれ
PPTX
PDF
PDF
PPTX
PDF
PPTX
STARD2015に学ぶ「診断精度の分析」の書き方
PDF
PDF
PPTX
20170608 srws第四回pubmed検索その2
PDF
PDF
PDF
PDF
PDF
PDF
Cmdstanr入門とreduce_sum()解説
PDF
PDF
More Related Content
PDF
PDF
PDF
PDF
PDF
PPTX
(実験心理学徒だけど)一般化線形混合モデルを使ってみた
PDF
PDF
StanとRでベイズ統計モデリング読書会 導入編(1章~3章)
What's hot
PDF
PPTX
PPTX
PDF
臨床疫学研究における傾向スコア分析の使い⽅ 〜観察研究における治療効果研究〜
PPTX
Rで因子分析 商用ソフトで実行できない因子分析のあれこれ
PPTX
PDF
PDF
PPTX
PDF
PPTX
STARD2015に学ぶ「診断精度の分析」の書き方
PDF
PDF
PPTX
20170608 srws第四回pubmed検索その2
PDF
PDF
PDF
PDF
PDF
PDF
Cmdstanr入門とreduce_sum()解説
Viewers also liked
PDF
PDF
PDF
PPTX
PPTX
PPTX
PDF
第2回DARM勉強会.preacherによるmoderatorの検討
PDF
PDF
DARM勉強会第3回 (missing data analysis)
PDF
PDF
PDF
PDF
Rによるやさしい統計学第20章「検定力分析によるサンプルサイズの決定」
PDF
PPTX
PDF
PDF
分類分析 (taxometric analysis)
PPTX
PDF
2012-1110「マルチレベルモデルのはなし」(censored)
PDF
Similar to Darm3(samplesize)
PDF
PDF
Analysis of clinical trials using sas 勉強用 isseing333
PDF
PDF
PPTX
PPTX
PPT
PDF
PPT
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PPTX
PPTX
PDF
Eureka agora tech talk 20170829
More from Yoshitake Takebayashi
PPTX
単一事例研究法と統計的推測:ベイズ流アプローチを架け橋として
PDF
単一事例研究法と統計的推測:ベイズ流アプローチを架け橋として (文字飛び回避版はこちら -> https://www.slideshare.net/yos...
PDF
フェーズI/IIに置けるベイジアン・アダプティブ・メソッド
PDF
PDF
PPTX
PPTX
PPTX
PPTX
マルコフ連鎖モンテカルロ法 (2/3はベイズ推定の話)
Darm3(samplesize) 1. 2. 3. 4. 5. 3 4 5 6 7
0.00.30.6
T
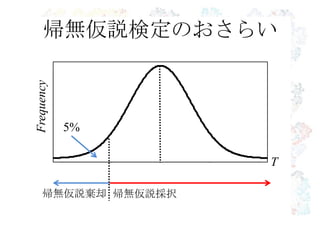
5%
帰無仮説検定のおさらい
帰無仮説採択帰無仮説棄却
Frequency
6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 対応のある2群の差
① d, g, Δをそのまま使う
※群間の相関を無視してるので不適
② 差得点の効果量を使う(反復測定で推奨: Glass et al., 1981)
12
2
2
2
1 2ssssD
第一群の分散 第一群の分散 共分散
※①と②のうちどれを使用するか研究者によって意見が異なる
D
D
D
s
M
d
差得点の平均
差得点の標準偏差(分母がn-1)
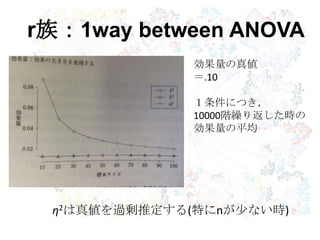
19. r族の効果量
① pearsonの積率相関 (連続変数同士の相関)
② 点双列相関係数 (2値と連続変数の相関)
③ 決定係数・分散説明率 :相関係数の2乗
yx
xy
ss
s
r
各変数の標準偏差
両変数間の共分散
21
21
qq
S
MM
rpb
データ全体の標準偏差
各群の比率
連続変数を2値変数で分割した各群の平均
1
1
2
)(
n
S
n
i
i xx
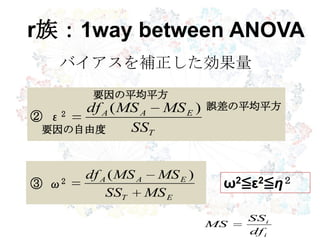
20. 21. 22. 23. 要因の分散
被験者内の分散
誤差の分散
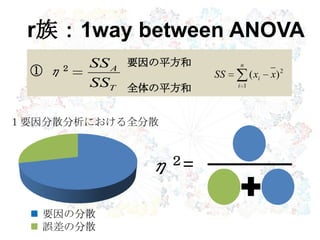
1要因分散分析における全分散
η2 =
η2
p =
r族:1way within ANOVA
EsA
A
SSSSSS
SS
EA
A
SSSS
SS
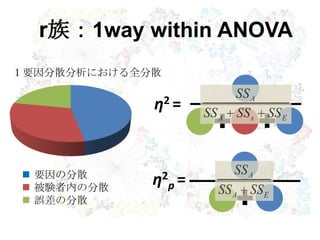
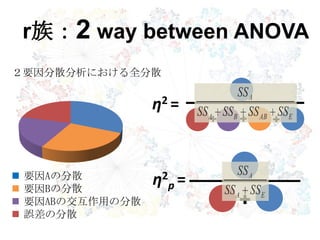
24. 25. 要因Aの分散
要因Bの分散
要因ABの交互作用の分散
誤差の分散
2要因分散分析における全分散
η2 =
η2
p =
r族:2 way between ANOVA
EABBA
A
SSSSSSSS
SS
EA
A
SSSS
SS
26. r族:2 way between ANOVA
22222
2
2
2
2
)(
)(
)(
EABBAT
EE
EAB
BA
AB
EB
B
B
EA
A
A
MS
MSMS
abn
dfdf
MSMS
abn
df
MSMS
abn
df ω2
ω2
p
2
2
T
AB
22
2
EAB
AB
2
2
T
A
22
2
EA
A
交互作用
交互作用
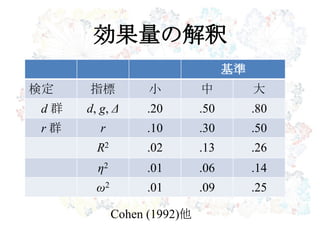
27. 28. 29. 効果量の解釈
基準
検定 指標 小 中 大
d 群 d, g, Δ .20 .50 .80
r 群 r .10 .30 .50
R2 .02 .13 .26
η2 .01 .06 .14
ω2 .01 .09 .25
Cohen (1992)他
30. 31. 32. 33. 3 4 5 6 7
0.00.30.6
平均
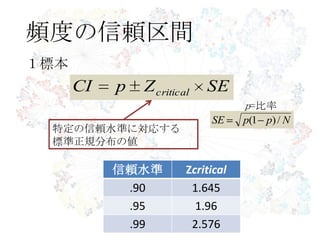
信頼水準
(95%)
0.25%0.25%
誤差範囲 誤差範囲
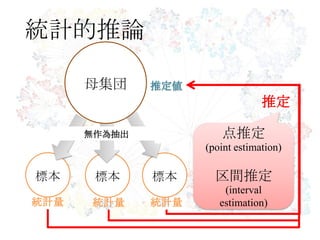
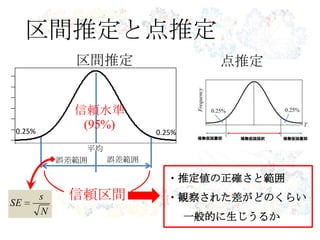
区間推定と点推定
区間推定
N
s
SE
信頼区間
・推定値の正確さと範囲
・観察された差がどのくらい
一般的に生じうるか
点推定
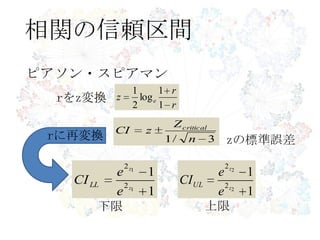
34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. 回帰分析の信頼区間
)( icriticali SEtCI ββ
重回帰分析
標準偏回帰係数(β)の信頼区間
決定係数(R2)の信頼区間
2
2
Rcritical SEtRCI
)3)(1(
)1()1(4
2
2222
2
nn
knRR
SER
1variablesNNdftの自由度
R2の標準誤差
47. 48. 49. 実行例
dat <- data.frame(y = c(9,12,13,15,16,8,12,11,10,14),
x = rep(factor(c("a","b")), each=5)
)
ind.t.test(y~x, data=dat, correct=FALSE)
Rpsychi:対応のないt検定
hedge’s g
50. 実行例
dat <- data.frame(y = c(9,12,13,15,16,8,12,11,10,14),
x = rep(factor(c("a","b")), each=5)
)
ind.t.test(y~x, data=dat, correct=FALSE)
Rpsychi:1要因の分散分析
hedge’s g
η2
51. 実行例
dat <- data.frame(
y = c(2,3,4,1,3,1,3,4,5,5,6,6,6,7),
A = factor(c(rep("A1",5), rep("A2", 9))),
B = factor(c(rep("B1",3), rep("B2",2), rep("B1",2), rep("B2",7)))
)
ind.twoway(y~A*B, data=dat)
Rpsychi:2要因の分散分析
η2p
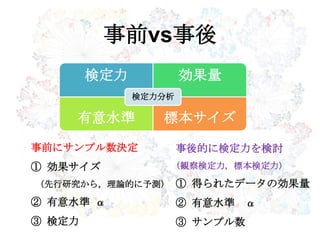
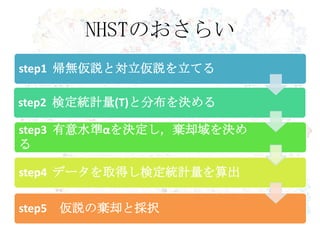
52. 53. 54. ⇒ 検出力 .80が推奨されてい
る (Cohen, 1992)
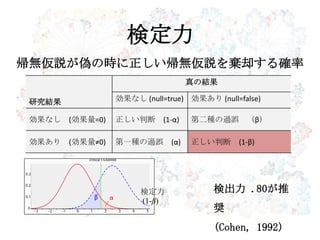
検定力
研究結果
真の結果
効果なし (null=true) 効果あり (null=false)
効果なし (効果量=0) 正しい判断 (1-α) 第二種の過誤 (β)
効果あり (効果量≠0) 第一種の過誤 (α) 正しい判断 (1-β)
検定力
(1-β)
帰無仮説が偽の時に正しい帰無仮説を棄却する確率
検出力 .80が推
奨
(Cohen, 1992)
55. 56. 57. 58. 検定力
検定力が高すぎる場合
わずかな(無意味な)差でも検出されやすくなる
t df p 平均値差
-2.296 999998 .022 .00
100万人の対応のない t 検定 (Field & Wright, 2006)
検定力が低すぎる場合
第2種の過誤が生じる (医学領域では倫理的に問題)
効果の強い薬v.s弱い薬
検定力の低いテストで比較
⇒両者の差を検出できない
⇒ 弱い薬が効果が強いと誤認されて使用される危険性
差は0でも検定結
果は「有意差あ
り」!?!?
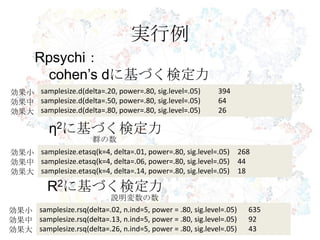
59. 60. 61. 62. 63. 実行例
samplesize.d(delta=.20, power=.80, sig.level=.05) 394
samplesize.d(delta=.50, power=.80, sig.level=.05) 64
samplesize.d(delta=.80, power=.80, sig.level=.05) 26
Rpsychi:
cohen’s dに基づく検定力
samplesize.etasq(k=4, delta=.01, power=.80, sig.level=.05) 268
samplesize.etasq(k=4, delta=.06, power=.80, sig.level=.05) 44
samplesize.etasq(k=4, delta=.14, power=.80, sig.level=.05) 18
η2に基づく検定力
群の数
効果小
効果中
効果大
効果小
効果中
効果大
samplesize.rsq(delta=.02, n.ind=5, power = .80, sig.level=.05) 635
samplesize.rsq(delta=.13, n.ind=5, power = .80, sig.level=.05) 92
samplesize.rsq(delta=.26, n.ind=5, power = .80, sig.level=.05) 43
R2に基づく検定力
説明変数の数
効果小
効果中
効果大
64. 65. 66. 67. 68. 69. 実行例
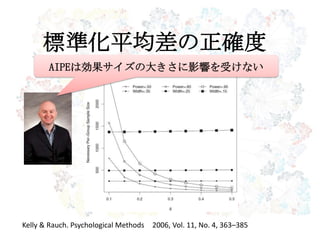
MBESS:
平均値差の正確度
ss.aipe.smd(delta=.20, conf.level=.95, width=.30) 344
ss.aipe.smd(delta=.50, conf.level=.95, width=.30) 353
ss.aipe.smd(delta=.80, conf.level=.95, width=.30) 369
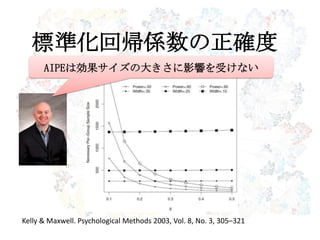
R2の正確度
効果小
効果中
効果大
ss.aipe.R2(Population.R2=.02, conf.level=.95, width=.10, which.width=“Full”, p=5)
178
ss.aipe.R2(Population.R2=.13, conf.level=.95, width=.10, which.width="Full", p=5)
617
ss.aipe.R2(Population.R2=.26, conf.level=.95, width=.10, which.width="Full", p=5)
879






















![母平均の信頼区間
criticalcritical tSEMCI
1標本の場合
平均=8
標準偏差=0.8
標本サイズ=48
t値=t(47)95%=2.01
23.00.801.2
48
8.0
0.8criticalCI
M = 8.0, 95% CI [7.77 8.23]
APAスタイル](https://image.slidesharecdn.com/darm3samplesize-130429075700-phpapp02/85/Darm3-samplesize-34-320.jpg)