1. ロジスティック回帰分析の入
門
- 予測モデル構築 -
2013/10/12
沖縄県立中部病院
宜保光一郎

2. 目次
•
•
•
•
•
① 予測モデルとは？
10 分
② なぜロジスティック回帰を使うのか？
( ここからが本番 )
③R でのモデル構築の実際
30 分
④ モデル評価
2

3. 予測モデルとは？
“Predictive modelling is the process by which a model
is created or chosen to try to best predict the
probability of an outcome” Predictive Inference: An
Introduction 1983
“I define predictive modeling as the process of applying
a statistical model or data mining algorithm to data
for the purpose of predicting new or future
observations.” Galit Shmueli “To Explain or to Predict?” Statical
Science 2010
3

4. 予測モデルと説明モデルの違い
予測モデル
説明モデル
こと
こと
この両者を区別して考える
関連 Association
因果 Causation
と、データサンプリング～
データ Data
理論 Theory
バリデーションまでの方法
前向き Prospective
後ろ向き Retrospective
論の違いが明確になってく
予測に合うように
理論に最も合うよう
る！
bias, variance を減らす にバイアスを減らす
4
Galit Shmueli “To Explain or to Predict?” Statical Science 2010

5. 予測モデルの種類
•
•
•
•
•
•
ロジスティック回帰→医学分野でよく使用
再帰分割法→決定木を使う方法
GAM→ 回帰モデルの発展型
Naïve Bayes
ニューラルネットワーク
(LASSO, リッジ回帰 )
5

6. ロジスティック回帰
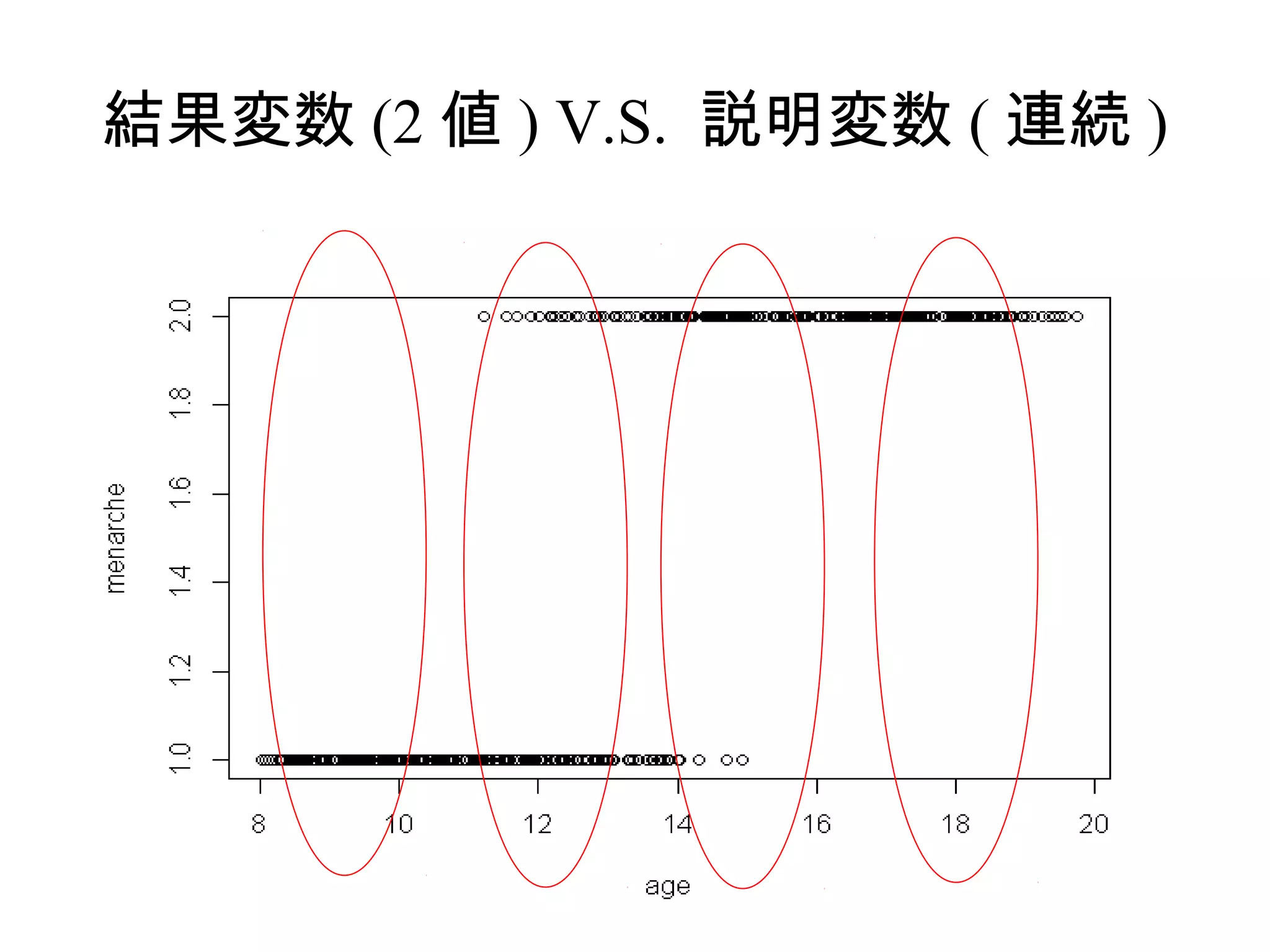
• 「回帰」とは結果変数 ( アウトカム ) と説
明変数の間に式を当てはめ、どれくらい
説明できるか定量化 ( 関連 ) したものであ
る
• 「打ち切りのない、結果変数が 2 値であ
るデータにはロジスティック回帰分析が
使われる。」
• なぜ？
6

7. 結果変数 (2 値 ) V.S. 説明変数 ( 連続 )
7

8. 8
10
12
14
newage2$age
16
8
0.0
0.2
0.4
rel.freq
0.6
0.8
1.0

9. 0.6
0.4
0.2
0.0
model1.prob
0.8
1.0
p=1 / 1+exp{-(β0+β1*X)}
8
10
12
14
newage$age
16
18
9

10. ロジット変換をすると…
ロジット変換
後
目的変数は確率のまま
-5
0
logit_model1
0.6
0.4
0.2
log(p/1-p)=β0+β1*Xi
0.0
model1.prob
0.8
5
1.0
p→log(p/1-p)
8
10
12
14
newage$age
16
18
8
10
12
14
newage$age
10
16
18

11. なぜロジスティックモデル？
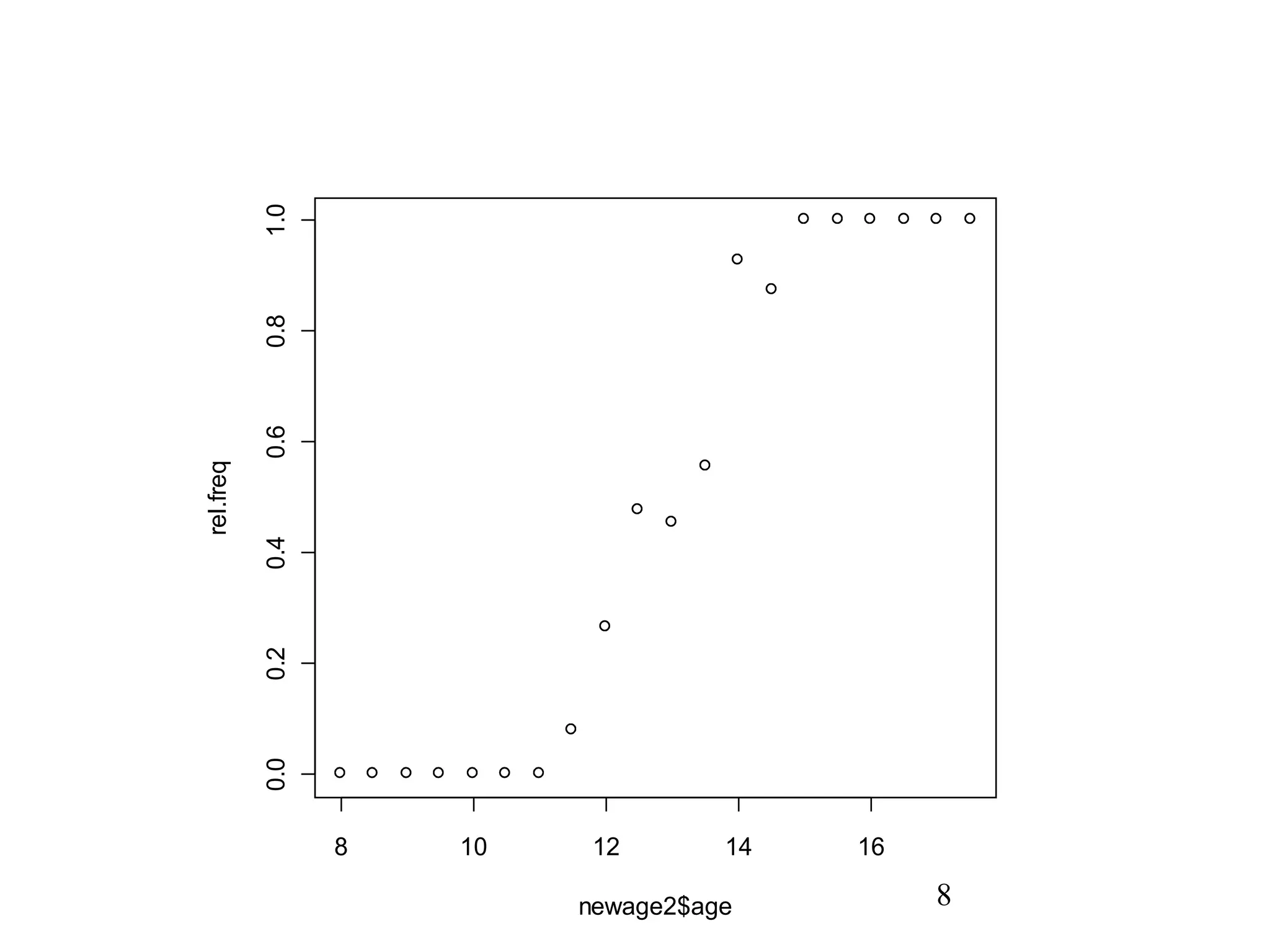
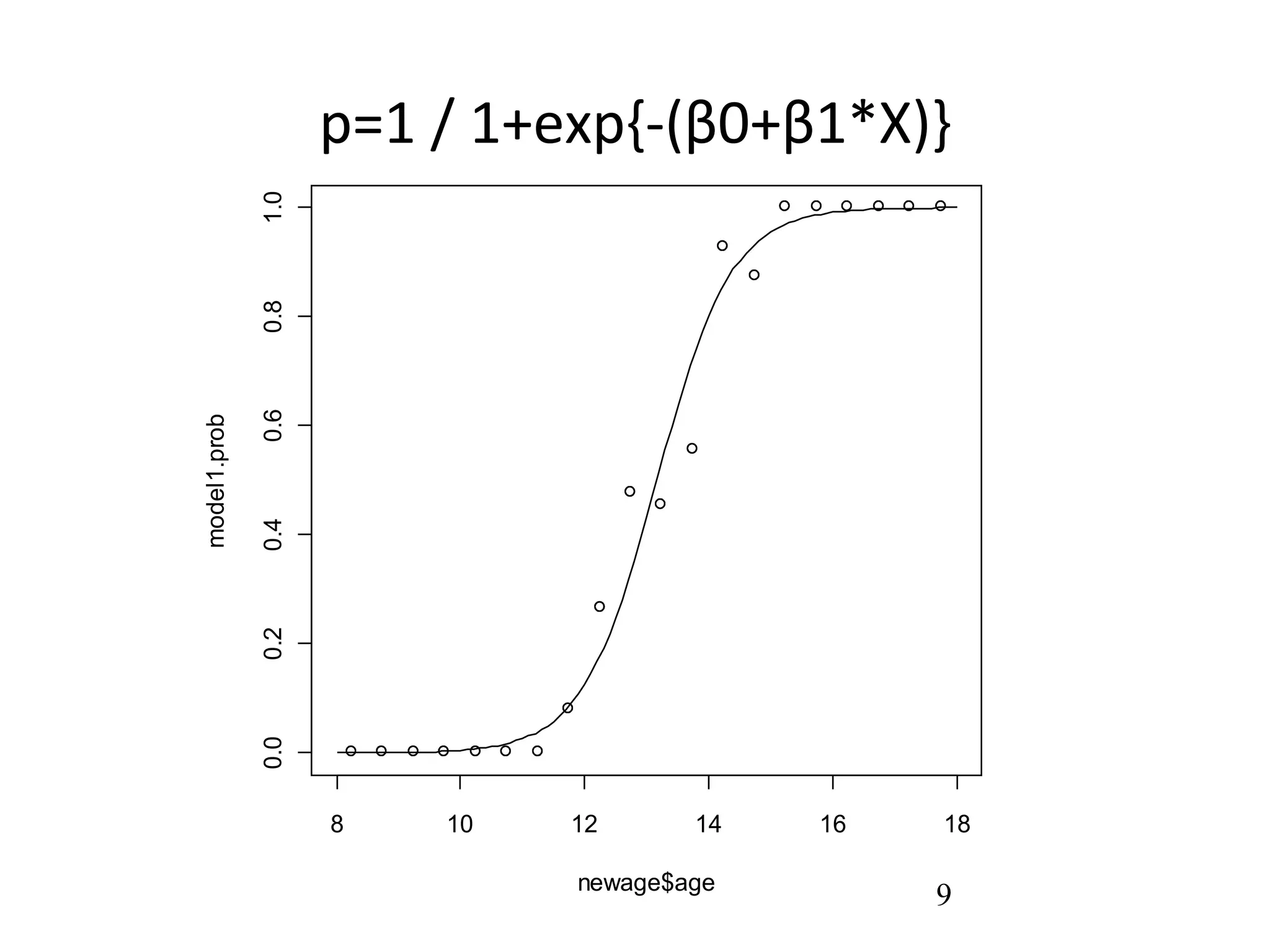
• 大きく 2 つの利点がある
– 1. アウトカムが 2 値データのときはシグ
モイドカーブが合理的
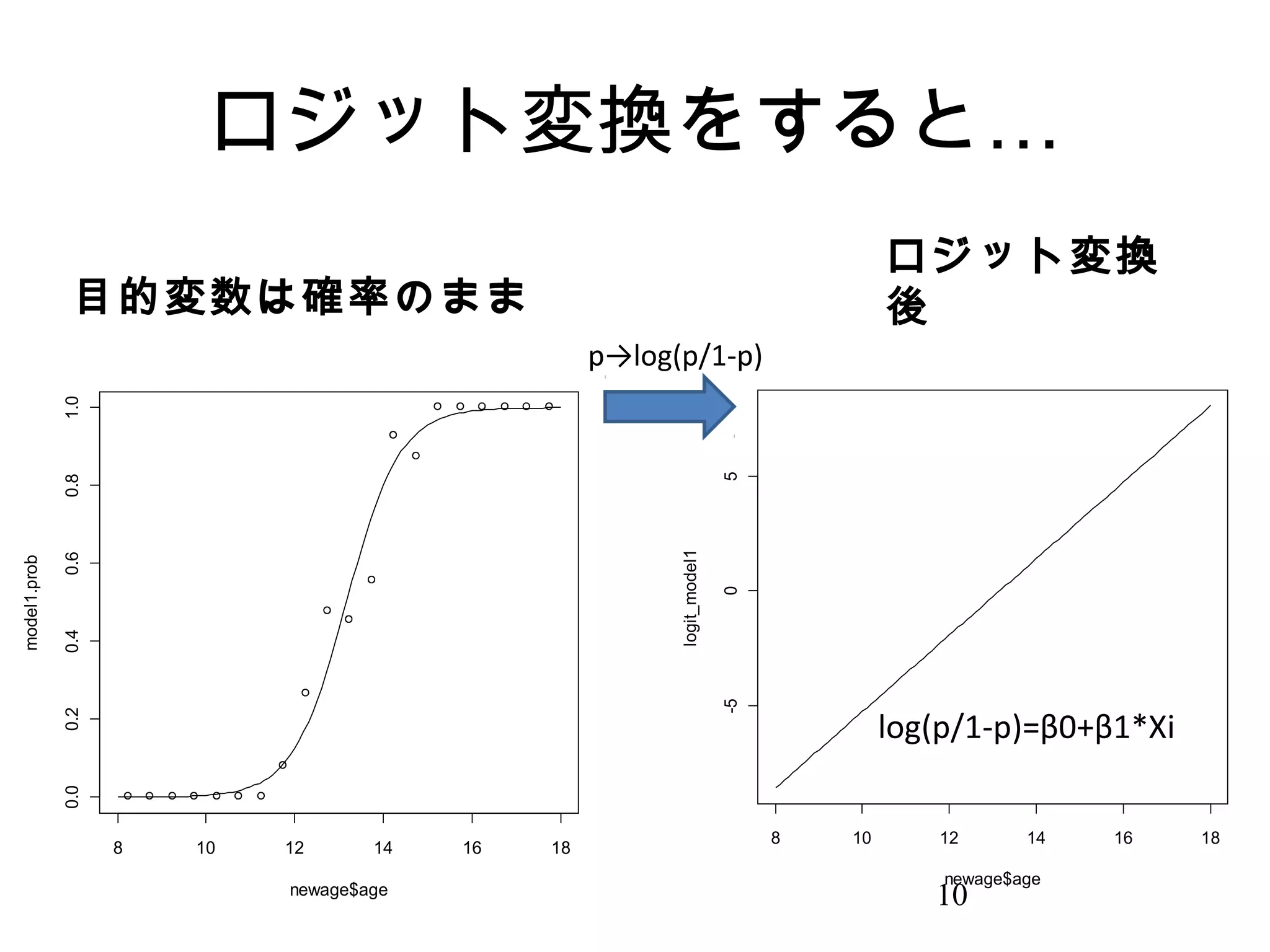
– 2. 係数が対数オッズになる。このため、
結果が理解されやすい→医者にとっては大
事
11

12. ロジスティック分析の流れ
• モデル作成 ( 変数選択→ main effect model→
交互作用項検討 )
• ↓
• モデル評価 (determination?calibration?)
• ↓
• Validation( 内的妥当性→外的妥当性 )
• ↓
• 完成。
12

13. R での使い方
• Hosmer-Lemeshow “Applied Logistic
regression” Wiley 2012 から
LowBirthWeightData
• N=189 、 11 の変数からなるデータセット
• R コーディングはハンドアウト
13

14. 予測モデルで何がしたいのか？
• 「科学的な興味として、低出生体重児 ( ア
ウトカム ) と、母体の妊娠時の喫煙との因
果関係を知りたい」→これは予測モデルで
は無い
• 「低出生体重児が生まれる確率を予測す
るために因果関係はどうでもいいが、モ
デルを作ってみたい」→予測モデル
14

15. 3 つのモデル
• null モデル ( 変数のないモデル )
• low~1
• 説明変数が一つだけのモデル
• low~smoke
• 多変数モデル
• low~smoke+age+race+lwt+smoke:race+age:sm
15
oke+age:race+smoke:age:race

16. smoke モデルの結果出力
Call:
glm(formula = low ~ smoke, family = binomial, data = lbw)
Deviance Residuals:
Min
1Q Median
3Q
Max
-1.0197 -0.7623 -0.7623 1.3438 1.6599
Wald 統計量≒ Z
Coefficients ： Estimate Std. Error z value Pr(>|z|)
(Intercept)
-1.0871 0.2147
-5.062 4.14e-07 ***
smokeYes
0.7041
0.3196
2.203
0.0276 *
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 234.67 on 188 degrees of freedom
Residual deviance: 229.80 on 187 degrees of freedom
AIC: 233.8
Number of Fisher Scoring iterations: 4
16

17. smoke モデルの結果出力
Call:
glm(formula = low ~ smoke, family = binomial, data = lbw)
尤度 (likelihood) とは「あるモデルで
Deviance Residuals:
Min
1Q Median
3Q
Max
現実のデータが得られる確率」
-1.0197 -0.7623 -0.7623 1.3438 1.6599
最尤法→尤度を最大化するパラメータ
Coefficients ： Estimate Std. Error z value Pr(>|z|)
の極値を得る方法 4.14e-07 ***
(Intercept)
-1.0871 0.2147
-5.062
smokeYes
0.7041
0.3196
2.203 0.0276 *
--Residual deviance = -2log(likelihood of fitted
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
model/ likelihood of saturated model)
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 234.67 on 188 degrees of freedom
Residual deviance: 229.80 on 187 degrees of freedom
AIC: 233.8
Number of Fisher Scoring iterations: 4
17

18. Null モデルの出力結果
•
•
•
•
•
•
•
•
•
•
•
•
•
•
glm(formula = low ~ 1, family = binomial, data = lbw)
Deviance Residuals:
Min
1Q Median
3Q
Max
-0.8651 -0.8651 -0.8651 1.5259 1.5259
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.790
0.157
-5.033 4.84e-07 ***
Residual deviance = -2log(likelihood of fitted
--model/ likelihood of saturated model)
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 234.67 on deviance(Saturated model) = 0
188 degrees of freedom
deviance(null model) = 234.67
Residual deviance: 234.67 on 188 degrees of freedom
deviance が小さいほどあてはまりは良
AIC: 236.67
い
Number of Fisher Scoring iterations: 4
18
AIC = Deviance + 2*N of parameter

19. smoke モデルの結果出力
Call:
glm(formula = low ~ smoke, family = binomial, data = lbw)
Deviance Residuals:
Min
1Q Median
3Q
Max
-1.0197 -0.7623 -0.7623 1.3438 1.6599
Coefficients ： Estimate Std. Error z value Pr(>|z|)
(Intercept)
-1.0871 0.2147
-5.062 4.14e-07 ***
smokeYes
0.7041
0.3196
2.203 0.0276 *
--Residual codes: 0 ‘***’ 0.001 ‘**’ 0.01 fitted ‘.’ 0.1 ‘ ’ 1
Signif. deviance = -2log(likelihood of ‘*’ 0.05
model/ likelihood of saturated model)family taken to be 1)
(Dispersion parameter for binomial
Null deviance: 234.67 on 188 degrees of freedom
Residual deviance: 229.80 on 187 degrees of freedom
AIC: 233.8
Number of Fisher Scoring iterations: 4
19
AIC = Deviance + 2*N of parameter

20. 多変数モデル
glm(formula = low ~ age + race + smoke + lwt + age:race + age:smoke +
age:lwt + race:smoke + race:lwt + smoke:lwt + age:race:smoke +
age:race:lwt + age:smoke:lwt + race:smoke:lwt + age:race:smoke:lwt,
family = binomial, data = lbw)
Deviance Residuals:
Min
1Q Median
3Q
Max
-1.4788 -0.9690 -0.5532 1.2638 2.3464
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept)
19.081932 18.327804 1.041 0.298
age
-0.801232 0.763315 -1.050 0.294
race
-9.656472 8.229436 -1.173 0.241
smokeYes
-25.658851 21.995005 -1.167 0.243
lwt
-0.138424 0.139208 -0.994 0.320
（以下略）
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 234.67 on 188 degrees of freedom
Residual deviance: 210.12 on 173 degrees of freedom
20
•AIC: 242.12

21. ロジスティック分析の流れ
• モデル作成 ( 変数選択→ main effect model→
交互作用項検討 )
• ↓
• モデル評価 (determination?calibration?)
• ↓
• Validation( 内的妥当性→外的妥当性 )
• ↓
• 完成。
21

22. どの変数を選択するか？
• 変数はどれを選択すべき？ smoke,race,age
は全て入れるべきなのか？ま
た、 smoke:race や smoke:age などの交互作
用はどうするか？
• アルゴリズム選択法 : P 値などを参考にし
て機械的に選択する方法、ステップワイ
ズ法など
• 強制投入法 : subject matter knowledg に基づ
22
いてそのままモデルに投入する方法

23. 変数選択
• Subject matter knowledge
• ニュアンスとしては、「アウトカムと変
数の関係について、先行研究や専門的な
見地から明らかな相関または因果がある
とわかっていること」
• 基本的に変数は subject matter knowledge に
基づいて選択される。 ( データは一切みな
い)
• 説明モデルでは機械的選択は推奨されな
23
い。でも予測モデルならありかも。

24. overfitting
• 強制投入法で問題はモデルに組み込む変
数が多くなりがちで、 overfitting という問
題を引き起こすことと、同様にサンプル
サイズとの兼ね合いでパワーの減少とい
う課題が生じる
• overfitting の結果、①予測因子の過大評価
(testimation bias) および、②モデルパフォ
ーマンスの過大評価 (optimism) が生じる
• また予測因子が多いモデルは現実的に使
24
いにくい

25. 変数選択まとめ
• 説明モデルであれば、強制投入法を行う
べき→もとの理論を元に構築するのだから
データは見ない。
• 予測モデルなら、基本は強制投入だが、
予測因子 ( 共変量、説明変数 s) が多くな
りすぎる場合は、アルゴリズムによる方
法などもあり。ただしその場合もステッ
プワイズ法は推奨されない
25

26. アルゴリズム選択
• いろいろあるが、どれが一番いいという
のはない。
• Hosmer, Lemeshow”Applied logistic
regression”→ purposeful selection
• Styerberg “Clinical Prediction Models”→
bayesian model averaging(Package”BMA”),
bootstrapping(Package”bootStepAIC”),
Lasso(Package”glmnet”)
• AIC
26

27. 交互作用項
• 交互作用も基本的に subject matter
knowledge に基づいて加える。
• 重要な交互作用の例 : Harrel “Regression
modeling strategies” より
• 年齢とリスク因子 (age:hypertension)
• 年齢と疾患のタイプ (age:diabetes)
• 人種と疾患
• 季節とある疾患 (season:diarrea)
27
• 症候同士 (consciousness:blood pressure)

28. Hierarchically well-formulated
• 例えば、 4 つの共変量があれば理論的には
10 通りの交互作用の組み合わせがある。
• 全てをモデルに投入すると前述した
overfitting 、パワーの問題が生じる
• 交互作用項を検討する原則 : Hierarchically
well-formulation
• 高次の交互作用項 (3way, 4way) はより低次
の交互作用項あるいは main effect に依存す
28

29. Example
• Outcome ~ P1 + P2 + P3 + P1:P2 + P1:P3 +
P2:P3 + P1:P2:P3
• これらの予測因子のの中で P1,P2 が現実的
に相互作用を起こしえない場合、 P1:P2 は
除去される。
• 同時により高次の交互作用項 P1:P2:P3 も
除去される (Hierarchically well-formulated)
• その後は統計学的検定により残すか決定
する
29

30. 例： lbw でのモデル構築
• アウトカムは low として予測モデルを構
築する
• subject matter knowledge は分かっていない
とする
• 全ての変数は smoke, race, age, lwt である。
• 強制投入はできないので、アルゴリズム
選択をしてみる。 purposeful selection
• Model: low~age+race+smoke+lwt 30

31. ロジスティック分析の流れ
• モデル作成 ( 変数選択→ main effect model→
交互作用項検討 )
• ↓
• モデル評価 (determination?calibration?)
• ↓
• Validation( 内的妥当性→外的妥当性 )
• ↓
• 完成。
31

32. モデルパフォーマンス評価
• Discrimination: c-statistics
• Calibration: Hosmer-Lemeshow test and
plotting
• Overall fit: pseudo-R^2
• Reclassification: NRI
• Clinical usefulness: decision curve
32
traditional
novel

33. Discrimination
• モデルによって、予測された結果が実際
観察されたアウトカムにどのくらい正確
に分類できているかという能力
• ROC カーブを描いて AUC=c statistics を求
めることが一般的
• Package”pROC”
33

34. ROC curve
34

35. Calibration
• モデルで予測された確率と、実際に観察
された確率がどれだけ一致しているかと
いう能力
• Calibration plot では、各々の対象について
の予測された確率を順番に並べ、それら
を 10 等分したものと、その区分けごとの
観察されたアウトカムの割合 ( 確率 ) を比
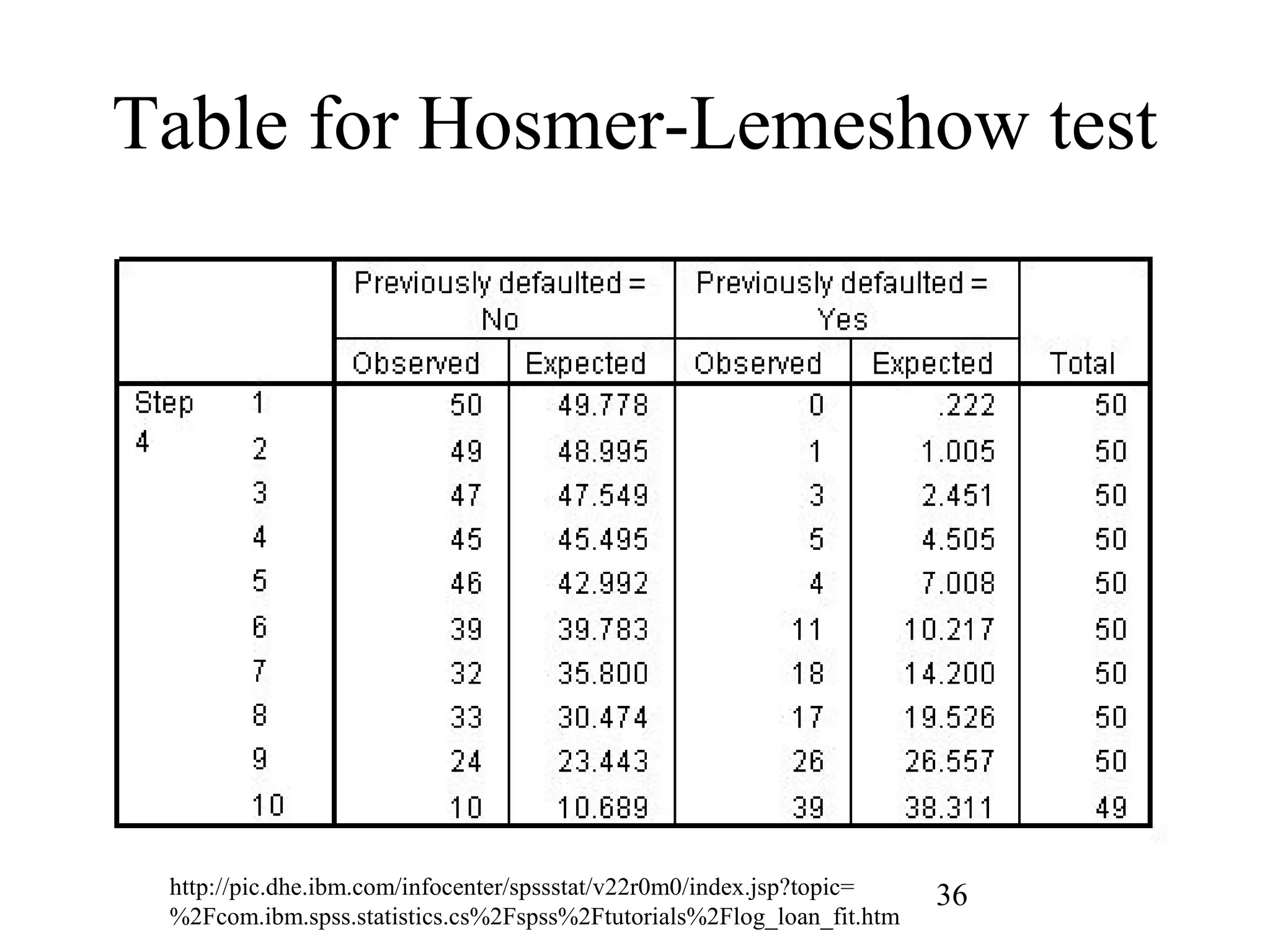
較し、プロットもしくは検定する
35

36. Table for Hosmer-Lemeshow test
http://pic.dhe.ibm.com/infocenter/spssstat/v22r0m0/index.jsp?topic=
%2Fcom.ibm.spss.statistics.cs%2Fspss%2Ftutorials%2Flog_loan_fit.htm
36

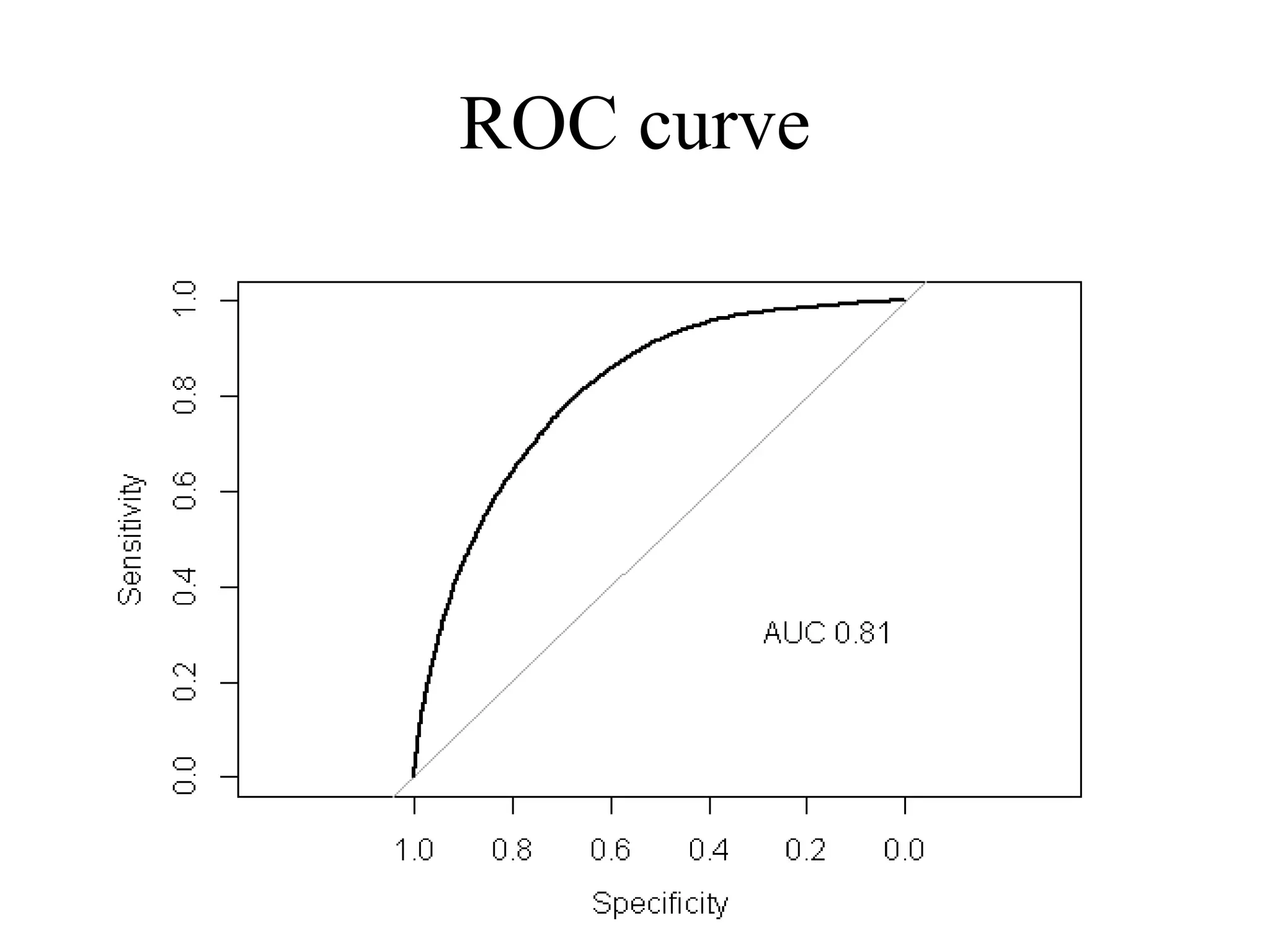
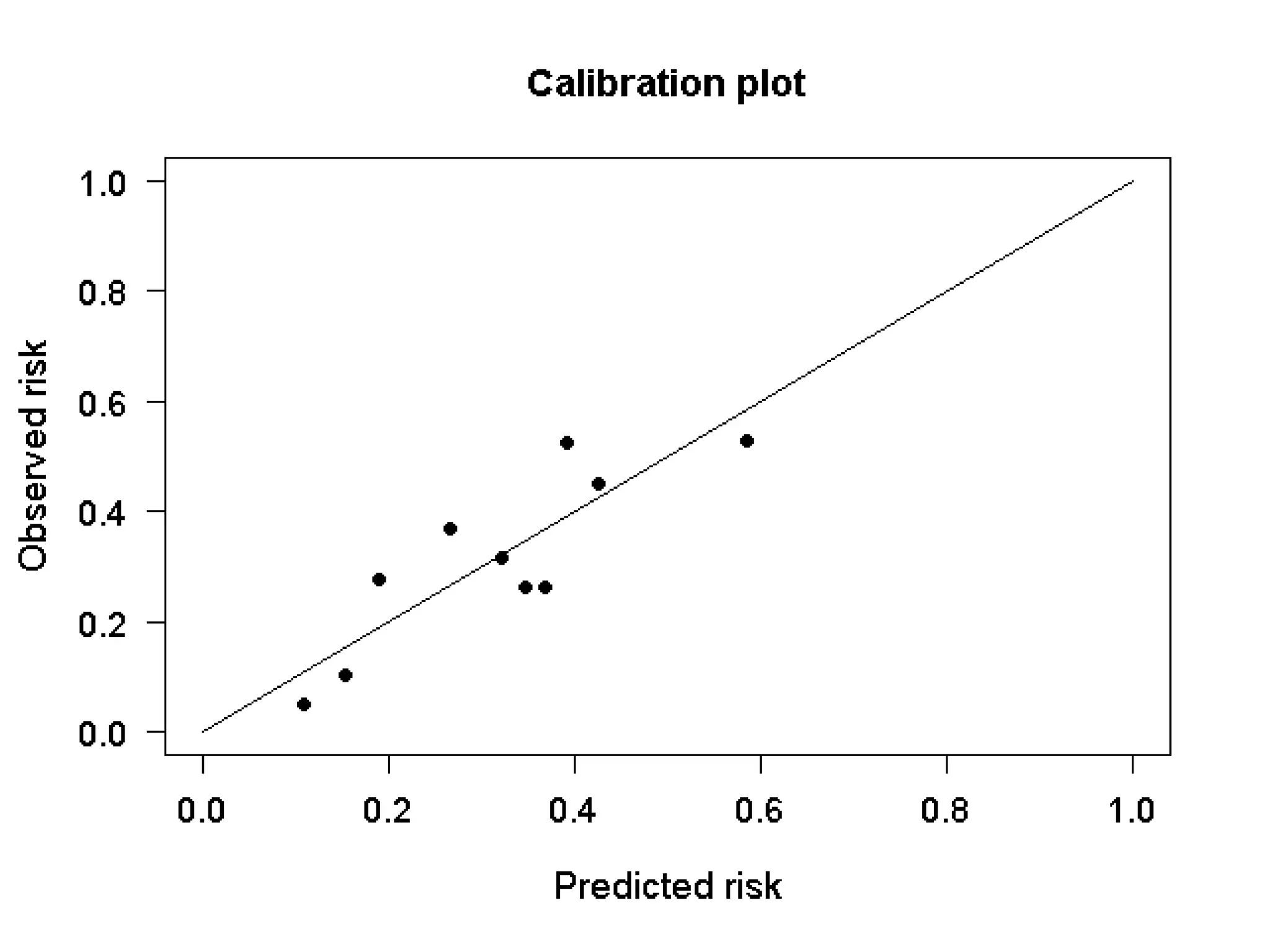
37. 37

38. Discrimination V.S. Calibration
• この両者はトレードオフの関係にある。
• アウトカムがすでに起きている ( 診断目的
など ) ものならば、アウトカムへの分類を
みる discrimination が良い。
• アウトカムがまだ起きていない ( 予後予測
など ) 場合は、リスクや確率で推測しなけ
ればならないので Calibration が重視され
る
• Cook et al. Circulation 2007
38

39. ロジスティック分析の流れ
• モデル作成 ( 変数選択→ main effect model→
交互作用項検討 )
• ↓
• モデル評価 (determination?calibration?)
• ↓
• Validation( 内的妥当性→外的妥当性 )
• ↓
• 完成
39

40. Validation
• Validation: とは
Population distribution
Setting 1
Setting 2
Setting 3
Sample 1
Sample 1
Sample 1
Internal Model 1
validation
External validation
40

41. 内的妥当性チェック
• “Optimism”
• モデルを作成したデータセットを用い
validation しても過大評価してしまう。こ
れを Optimism という。
• これを避けるための一般的な方法はデー
タを split して、 derivation set ( モデル作成
用 ) と test set ( バリデーション用 ) に分け
る方法である
41

42. 内的妥当性のチェック
• 他には Cross-validation や Bootstrap を使っ
て、擬似的にデータセットを作成してバ
リデーションする方法もある。
• ハンドアウト参照
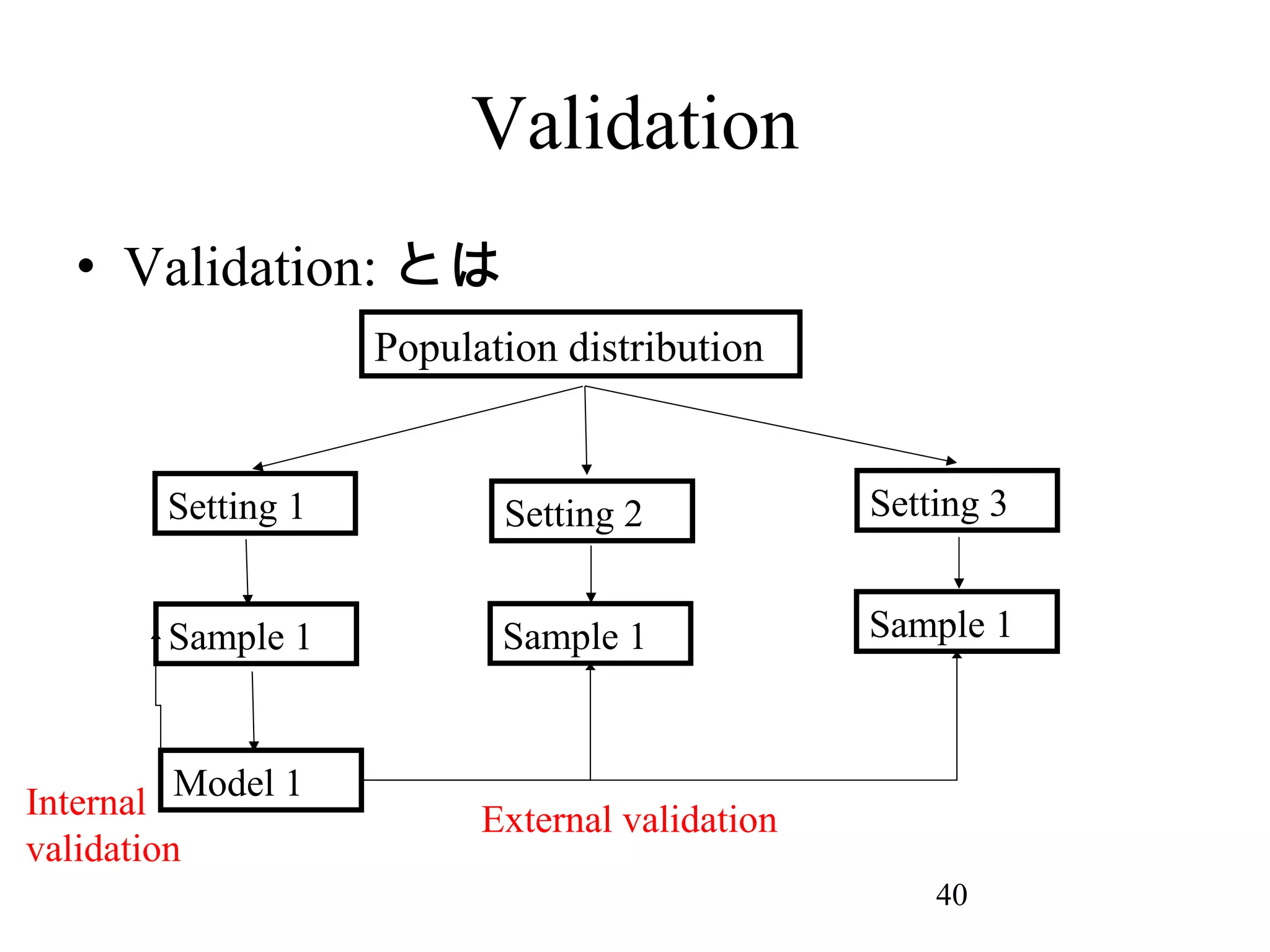
• Package”rms”
42

43. 外的妥当性 = 一般化可能性
• 外部データを用いて評価する。
• 外部データとは時間的、空間的に離れて
いる、または独立した他者による検討さ
れるものである。
• 外的妥当性のチェックでは、モデルパフ
ォーマンスが低下することが多い。その
場合、 re-calibration などといった、モデル
に少し手を加えるリペア法もいくつか存
在する。
43

44. 予測モデル V.S. 説明モデル
• モデルアセスメントの観点
• 予測モデル→一般化できるかが問題なので
、 validation が大事
• 説明モデル→理論を上手く説明できている
かが大事なので、 goodness-of-fit や残差診
断などが大事になる
44

45. 参考文献
• Hosmer, Lemeshow “Applied Logistic Regression 3rd
ed.” Wiley 2013
• Steyerberg “Clinical Prediction Models” Springer 2009
• Harrell “Regression Modeling Strategies” Springer
2001
• Kleinbaum “Logistic regression 3rd ed” Springer 2010
• Jaccard “Interaction effects in logistic regression”
SAGE 2001
• Shmueli “To Explain or to Predict?” Statical Science
2010
45