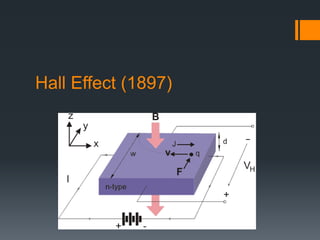
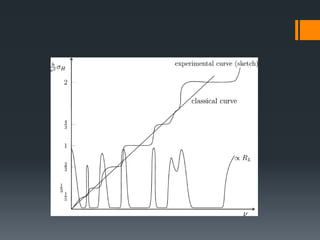
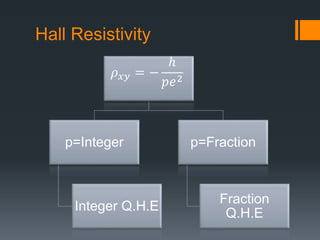
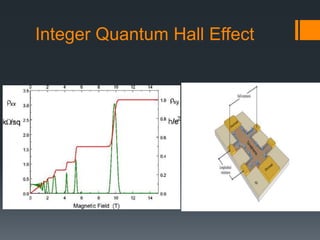
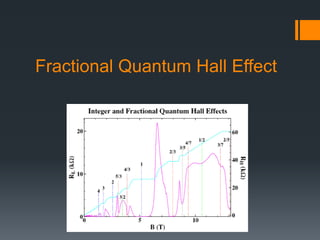
This document summarizes the quantum Hall effect. It describes the conditions needed to observe the effect including low temperatures, strong magnetic fields, and using a MOSFET. The quantum Hall effect results in the Hall resistivity being quantized as integers or fractions of h/e^2 depending on if it is the integer or fractional quantum Hall effect. The integer effect can be explained by considering non-interacting electrons forming discrete Landau levels. The fractional effect involves strongly interacting electrons condensing into an incompressible liquid state where quasiparticles have fractional charge.

1. QUANTUM HALL
EFFECT
SUBMITTED TO: Prof. R.S SINGH
SUBMITTED BY: VISHAL KUMAR JANGID,M.Sc(Final) 2016-17
JNVU (Department of Physics)

2. Hall Effect (1897)

3. Quantum Hall Effect(1980)
CONDITION
EXPERIMENT
EXPECTATION
• If the motion of electron
is restricted to x-y plane.
• Low temperature
• Strong magnetic field
• MOSFET
• Similar result as we
obtain in hall effect

5. Hall Resistivity
𝜌 𝑥𝑦 = −
ℎ
𝑝𝑒2
p=Integer
Integer Q.H.E
p=Fraction
Fraction
Q.H.E

6. Integer Quantum Hall Effect

7. Explanation IQHE
 It can be explain by considering non interacting electron.
 At high magnetic field B, the electronic density of states
becomes a set of discrete Landau levels due to the
confinement produced by the field.
 When these levels are well resolved, if a voltage is applied
between the ends of a sample, the voltage drop between
voltage probes along the edge of a sample can go to zero in
particular ranges of B, and the Hall resistance becomes
extremely accurately quantised

8. Continue ….
 The QHE can be described in terms of a set of states, one per
Landau level, travelling along the edges.
 energy E=𝐸1 + (𝑛 + 1/2)ђ𝜔 ± 𝜇 𝐵 𝐵

9. Fractional Quantum Hall Effect

10. Explanation
 By considering a two-dimensional system of strongly interacting
electrons.
 At particular magnetic fields, the electron gas condenses into a
remarkable state with liquid-like properties
 Filling factor: 𝑝 =
𝑛
𝑚
, where m is always turn out to be odd
number
 FRACTIONALLY-CHARGED QUASIPARTICLES :
consider quasiparticles with charge e*=e/q
 COMPOSITE FERMIONS:
 it attaches two (or, in general, an even number) flux
quanta h/e to each electron, forming integer-charged
quasiparticles called Composite Fermions

11. Thank you