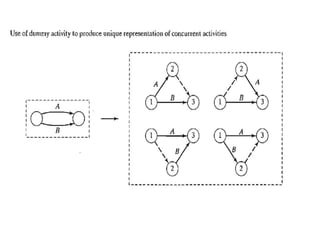
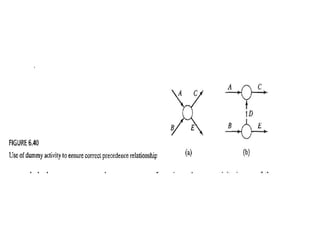
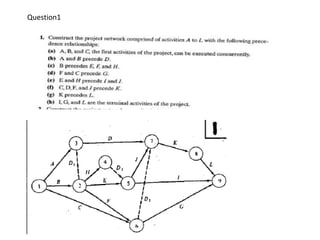
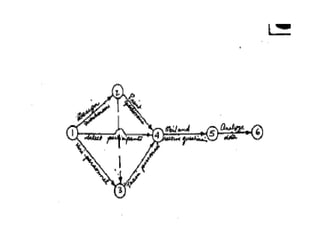
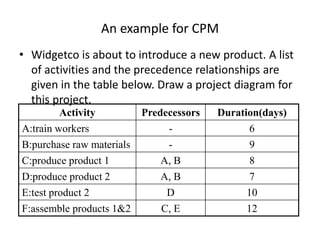
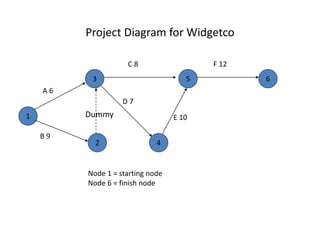
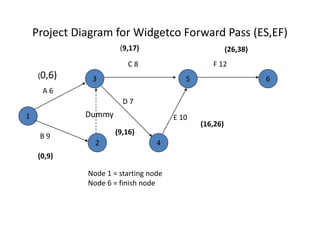
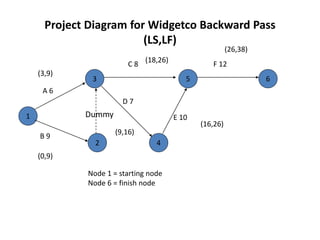
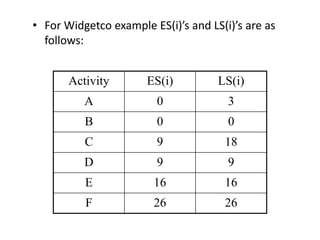
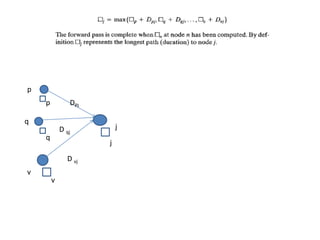
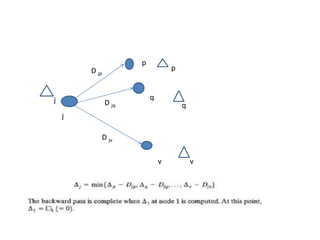
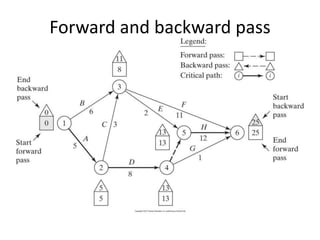
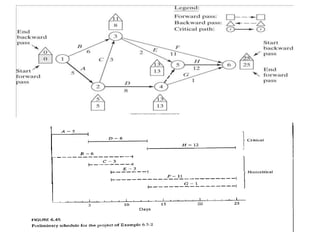
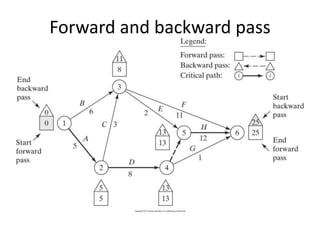
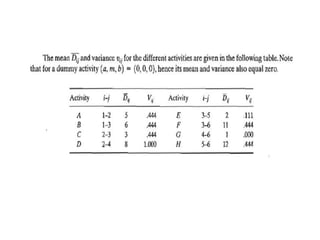
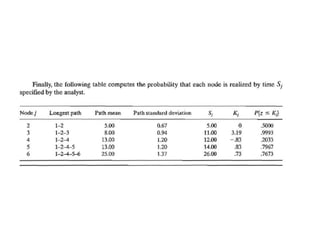
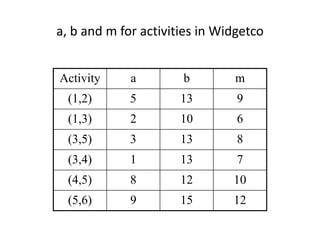
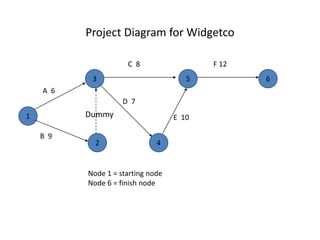
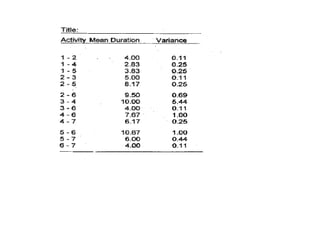
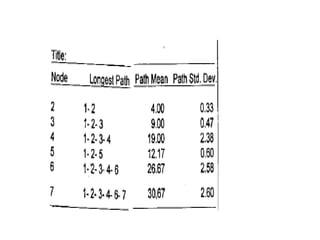
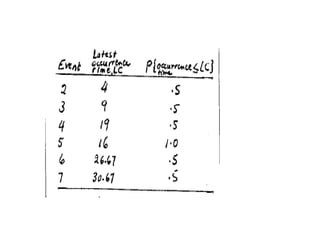
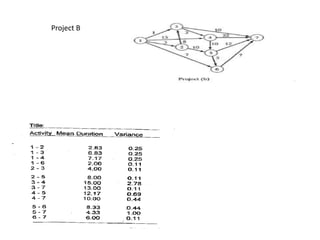
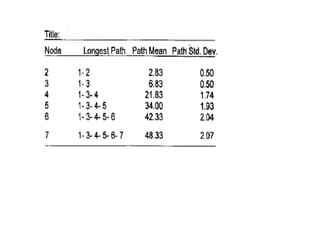
The document discusses the Critical Path Method (CPM) and Program Evaluation and Review Technique (PERT) for project scheduling. CPM determines the minimum project duration when activity times are known with certainty, while PERT estimates the probability of completing on time when activity times are uncertain. Both methods represent projects as networks and identify critical paths that must be followed to complete on schedule.